河南省开封市2023-2024学年七年级上学期期末数学试题

这是一份河南省开封市2023-2024学年七年级上学期期末数学试题，共19页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。


一、单选题
1．2024的倒数是（ ）
A．B．2024C．D．
2．2023年10月18日，中国开封第41届菊花文化节期间，招商引资推介暨产业合作交流会同期举办，开封市共签约项目92个，总投资规模约443.43亿元，涉及制造业、现代服务业、文化旅游、农业产业化、科技文卫以及金融等领域．将数据“443.43亿”用科学记数法表示为（ ）
A．B．C．D．
3．下列式子，，0，，中，整式有（ ）
A．2个B．3个C．4个D．5个
4．下列计算中，正确的是（ ）
A．B．C．D．
5．如果单项式与是同类项，那么关于的方程的解为（ ）
A．B．C．D．
6．将“青春用来奋斗”6个汉字分别写在某正方体的表面上，如图是它的一种平面展开图，则在原正方体中，与“春”字所在的面相对的面上的汉字是（ ）
A．青B．来C．斗D．奋
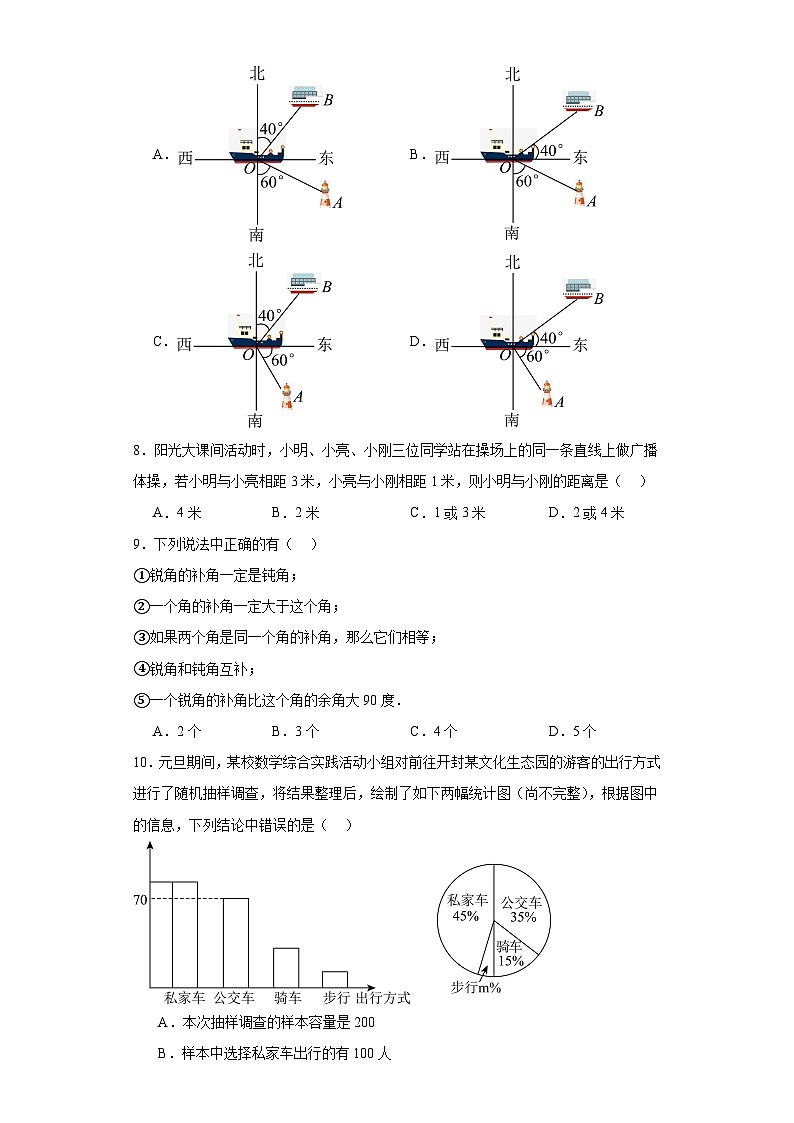
7．货轮在航行过程中，发现灯塔在它南偏东的方向．同时，在它北偏东方向上又发现了客轮，则下列图形表示正确的是（ ）
A．B．
C．D．
8．阳光大课间活动时，小明、小亮、小刚三位同学站在操场上的同一条直线上做广播体操，若小明与小亮相距3米，小亮与小刚相距1米，则小明与小刚的距离是（ ）
A．4米B．2米C．1或3米D．2或4米
9．下列说法中正确的有（ ）
①锐角的补角一定是钝角；
②一个角的补角一定大于这个角；
③如果两个角是同一个角的补角，那么它们相等；
④锐角和钝角互补；
⑤一个锐角的补角比这个角的余角大90度．
A．2个B．3个C．4个D．5个
10．元旦期间，某校数学综合实践活动小组对前往开封某文化生态园的游客的出行方式进行了随机抽样调查，将结果整理后，绘制了如下两幅统计图（尚不完整），根据图中的信息，下列结论中错误的是（ ）
A．本次抽样调查的样本容量是200
B．样本中选择私家车出行的有100人
C．扇形统计图中的为5
D．若元旦期间去该地观光的游客有1000人，则选择私家车方式出行的大约有450人
11．如图.把同样大小的围棋子按照一定规律摆放，其中第①个图形中共有3个棋子，第②个图形中共有7个棋子，第③个图形中共有13个棋子，…，如此规律排列，则第10个图形中棋子的个数为（ ）
A．91B．103C．111D．133
二、填空题
12．对单项式“”可以解释为：一件商品原价为a元，若按原价的6折出售，这件商品现在的售价是元，请你对“”再赋予一个含义： ．
13．若，则 ．
14．如图，点在直线上，射线平分，若，则 ．
15．《九章算术》是中国传统数学最重要的著作之一．书中记载：“今有人共买鸡，人出九，盈十一；人出六，不足十六．问人数几何？”意思是：“有若干人共同出钱买鸡，如果每人出九钱，那么多了十一钱；如果每人出六钱，那么少了十六钱．问：共有几个人？”设共有个人共同出钱买鸡，根据题意，可列一元一次方程为 ．
16．如图，用三角板经过直线外一点画这条直线的垂线，这样的垂线只能画出一条．这里面蕴含的数学道理是 ．
17．已知数轴上的两点，分别表示数，3，若点与点的距离为5个单位长度，则点表示的数是 ．
三、解答题
18．计算：
(1)
(2)
19．解方程：
(1)；
(2)
20．已知，，求的度数．抄写下面的解答过程并填空（理由或数学式）．
解：∵（已知）
（ ）
∴（ ）（等量代换）
∴（ ）
∴（ ）
∵（ ）
∴（ ）
21．先化简，再求值：，其中，．
22．如图，点在线段上，点是线段的中点，．
(1)延长线段到，使（请你依据题意，补全图形）；
(2)在（1）的条件下，若，求线段的长度．
23．某快递员骑电动车送快递，某天在一条东西方向的路上行驶，从地出发，约定向东走为正，当天的行走记录如下（单位／千米）：
．
(1)收工时，快递员在地的哪个方向？求此时快递员与地的距离．
(2)若电动车每千米耗电0.02度，求该天共耗电多少度．
24．小红卧室的窗户上半部分是由4个扇形组成的半圆形，下半部分为4个大小一样的长方形组成的大长方形，小长方形的长和宽的比为，已知小长方形的长为．
(1)求这个窗户的面积和窗户外框的总长．
(2)小红想给窗户上方做装饰物，装饰物所占的面积为上半部分半圆面积的．求窗户中能射进阳光的部分的面积（窗框面积忽略不计）．
25．综合与实践课上，老师让同学们以“长方形的折叠”为主题开展数学探究活动．

(1)操作判断
操作一：把长方形对折，折痕交于点，交于点，把纸片展平；
操作二：将对折，点落在直线上的点处，得折痕；
操作三：将对折，点落在直线上的点处，得折痕，如图①．根据以上操作直接写出的度数：________．
(2)问题探究
若操作一中的点为上（不与，重合）的任意一点，如图②，的大小是否改变，请说明理由．
(3)拓展延伸
按照操作二、操作三，使与重合，折痕为；与重合，折痕为．如图③，请直接写出度度数．
26．某校准备采购一批足球和篮球，采购分三次完成，其中有一次购买时，足球和篮球的价格同时打折，其余两次均按标价购买，三次购买足球和篮球的数量及费用如下表所示：
(1)这三次采购中，第________次购买足球、篮球打了折扣；
(2)求每个足球及每个篮球的标价；
(3)根据（1）中的信息，若足球、篮球打折相同，求超市打几折销售.
27．问题情景：
数学活动课上，小明发现右图中蕴含着一个数学模型．
数学思考：
如图①，若，点在，之间，连接，，则，请说明理由．
拓展探究：
小明还发现若改变点的位置，如图②，若点在上方，连接，，则，，依然存在一定的数量关系，请认真思考后得出结论，并进行证明．
问题解决：
如图③，，点在射线上运动，，．请直接写出的度数．
足球的数量（个）
篮球的数量（个）
总费用（元）
第一次采购
1
1
140
第二次采购
6
8
1000
第三次采购
8
10
1024
参考答案：
1．A
【分析】本题主要考查了倒数，解题的关键是熟练掌握倒数的定义，“乘积为1的两个数互为倒数”．
【详解】解：2024的倒数．
故选：A．
2．A
【分析】根据科学记数法的表示方法：为整数，进行表示即可，确定的值，是解题的关键．
【详解】解：亿；
故选A．
3．C
【分析】本题主要考查了整式的识别，根据整式是多项式和单项式的统称进行求解即可．
【详解】解：下列式子，，0，，中，整式有，，0，，共4个，
故选：C．
4．D
【分析】本题考查合并同类项．根据合并同类项的法则，逐一进行判断即可．
【详解】解：A、，计算错误，此选项不符合题意；
B、，计算错误，此选项不符合题意；
C、，不能合并，此选项不符合题意；
D、，计算正确，此选项符合题意；
故选D．
5．C
【分析】本题主要考查了同类项的定义，解一元一次方程，一元一次方程解的定义，所含字母相同，相同字母指数也相同的单项式叫做同类项，据此得到，则，再解方程即可得到答案．
【详解】解：∵单项式与是同类项，
∴，
∴，
∴方程即为，
解得，
故选：C．
6．D
【分析】本题考查了正方体的展开图中相对两个面上的文字，注意正方体的平面展开图中相对的两个面一定相隔一个小正方形．利用正方体及其表面展开图的特点解题即可．
【详解】解：由正方体展开图的特点可知，与“春”字所在的面相对的面上的汉字是“奋”，
与“青”字所在的面相对的面上的汉字是“来”，与“用”字所在的面相对的面上的汉字是“斗”，
故选：D．
7．A
【分析】本题主要考查了方向角表示位置，正确理解方向角的定义是解题的关键．
【详解】解：∵灯塔在货轮南偏东方向上，
∴，
∵客轮在货轮北偏东方向上，
∴，
∴四个选项中，只有A选项表示正确，符合题意，
故选：A．
8．D
【分析】本题考查有理数运算的实际应用．分小明和小刚在小亮的同侧和异侧，两种情况列出算式计算即可．
【详解】解：当小明和小刚在小亮的同侧时：小明与小刚的距离是米；
当小明和小刚在小亮的异侧时：小明与小刚的距离是米；
故选：D．
9．B
【分析】本题考查余角和补角，根据和为90度的两个角互为余角，和为180度的两个角互为补角，逐一进行判断即可．
【详解】解：锐角的补角一定是钝角；故①正确；
一个角的补角不一定大于这个角，也可能等于或小于这个角，例如：90度角的补角也是90度，两角相等；故②错误；
如果两个角是同一个角的补角，那么它们相等；故③正确；
锐角和钝角不一定互补，和为180度时才互补；故④错误；
一个锐角的补角比这个角的余角大90度；故⑤正确；
综上；正确的有3个；
故选：B．
10．B
【分析】本题考查条形图和扇形图的综合应用．从统计图中有效的获取信息，是解题的关键．用乘公交车的人数除以三占比例求出样本容量判断A，用样本容量乘以私家车出行的比例，求出私家车出行的人数判断B，用1减去其它的出行方式所占的百分比，求出的值，判断C，样本估计总体的思想判断D．
【详解】解：A、本次抽样调查的样本容量是，选项正确，不符合题意；
B、样本中选择私家车出行的有人，选项错误，符合题意；
C、，故扇形统计图中的为5，选项正确，不符合题意；
D、若元旦期间去该地观光的游客有1000人，则选择私家车方式出行的大约有人；选项正确，不符合题意；
故选B．
11．C
【分析】本题主要考查了图形类的规律探索，观察图形可得，将图形分为两部分，上面部分为正整数的平方，下面从2开始，依次增加1，据此求解即可．
【详解】解：第1个图有个棋子，
第2个图有个棋子，
第3个图有个棋子，
第4个图有个棋子，
……，
以此类推可知，第n个图形有个棋子，
∴第10个图形中棋子的个数为，
故选：C．
12．练习本每本元，某人买了a本，共付款
【分析】本题考查了代数式的含义，根据单价乘以数量等于销售额，可得答案．
【详解】解：对“”再赋予一个含义：练习本每本元，某人买了a本，共付款，
故答案为：练习本每本元，某人买了a本，共付款．
13．
【分析】本题考查代数式求值，涉及绝对值非负性、平方的非负性、非负式和为0的条件，乘方运算等知识，根据非负式和为0得到，求出的值代入代数式即可得到答案，熟记非负式和为0的条件是解决问题的关键．
【详解】解：，
，解得，
，
故答案为：．
14．/108度
【分析】本题考查与角平分线有关的计算，根据角平分线平分角，得到，再根据平角的定义，求解即可．找准角度之间的数量关系，和差关系，是解题的关键．
【详解】∵平分，，
∴，
∴；
故答案为：．
15．
【分析】根据“鸡的价钱=9×人数—11；鸡的价钱=6×人数+16”即可列出方程.
【详解】共有个人共同出钱买鸡，根据题意，则有
9x-11=6x+16，
故答案为9x-11=6x+16.
【点睛】本题考查了一元一次方程的应用，弄清题意，找准等量关系列出方程是解题的关键.
16．在同一平面内，过一点有且只有一条直线与已知直线垂直
【分析】根据垂线的性质：在同一平面内，过一点有且只有一条直线与已知直线垂直，进行作答即可．
【详解】解：由题意，蕴含的数学道理是：在同一平面内，过一点有且只有一条直线与已知直线垂直；
故答案为：在同一平面内，过一点有且只有一条直线与已知直线垂直．
17．或
【分析】本题考查数轴上两点的距离．根据两点见的距离公式，分点在点的左侧和右侧两种情况，列式计算即可．
【详解】解：由题意，得：点表示的数是或；
故答案为：或．
18．(1)
(2)
【分析】本题主要考查了有理数的加减计算，含乘方的有理数混合计算：
（1）根据有理数的加减计算法则求解即可；
（2）按照先计算乘方，再计算乘除法最后计算加减法，有括号先计算括号的运算顺序求解即可．
【详解】（1）解：原式
；
（2）解：原式
．
19．(1)
(2)
【分析】本题考查解一元一次方程．掌握解一元一次方程的步骤，正确的计算，是解题的关键．
（1）移项，合并同类项，系数化1，求解即可；
（2）去分母，去括号，移项，合并同类项，系数化1，求解即可．
【详解】（1）解：，
移项，得：，
合并，得：，
系数化1，得：；
（2）去分母得：，
去括号，得：，
移项，合并，得：．
20．见解析
【分析】本题考查平行线的判定和性质．根据对顶角相等，平行线的判定和性质，平角的定义，进行作答即可．掌握平行线的判定和性质，是解题的关键．
【详解】解：∵（已知）
（对顶角相等）
∴（等量代换）
∴（同旁内角互补，两直线平行）
∴（两直线平行，同位角相等）
∵（平角的定义）
∴．
21．，
【分析】本题考查整式加减中的化简求值．去括号，合并同类项，化简后代值计算即可．
【详解】解：原式；
当，时，原式．
22．(1)见解析
(2)
【分析】本题主要考查了与线段中点有关的线段和差计算，线段的尺规作图：
（1）以D为圆心，以线段的长为半径画弧交线段延长线于E，点E即为所求；
（2）根据线段中点的定义得到，进而得到，则，即可得到．
【详解】（1）解：如图所示，点E即为所求；
（2）解：∵，点是线段的中点，
∴，
∵，
∴
∴，
∴，
∴．
23．(1)收工时，快递员在地的东面20千米处
(2)该天共耗电度
【分析】本题考查有理数运算的实际应用．读懂题意，正确的列出算式，是解题的关键．
（1）将所有数据相加后，根据和的情况进行判断即可；
（2）用总路程乘以每千米的耗电，进行求解即可．
【详解】（1）解：；
∴收工时，快递员在地的东面20千米处；
（2）快递员的总路程为：（千米）；
（度）．
答：该天共耗电度．
24．(1)这个窗户的面积为，窗户外框的总长为
(2)
【分析】本题主要考查了整式加减的应用：
（1）先求出小长方形的宽为，再根据窗户的面积等于下面4个小长方形面积加上半圆面积求出窗户的面积，窗户外框的总长等于下面大长方形的周长减去一个长再加上半圆周长即可求出答案；
（2）用窗户面积减去装饰物面积即可得到答案．
【详解】（1）解；由题意得，小长方形的宽为，
∴这个窗户的面积为，窗户外框的总长为
（2）解：
，
∴窗户中能射进阳光的部分的面积为．
25．(1)
(2)，其大小不变，理由见解析
(3)
【分析】本题主要考查了折叠的性质：
（1）根据折叠的性质得到，进而得到，则；
（2）由折叠的性质可得，由平角的定义可得，则；
（3）同（2）可知，由折叠的性质可得，则．
【详解】（1）解：由折叠的性质可得，，
∴，
故答案为：；
（2）解：，其大小不变，理由如下：
由折叠的性质可得，
∵，
∴，
∴，其大小不变；
（3）解：同（2）可知，
由折叠的性质可得，
∴．
26．(1)三
(2)每个足球的标价为元，则每个篮球的标价为元．
(3)超市打8折销售．
【分析】（1）本题根据购买1个足球和1个篮球所需费用，去对比第二次和第三次采购的费用，即可解题．
（2）本题考查一元一次方程与实际问题，设每个足球的标价为元，则每个篮球的标价为元，根据的二次采购的情况列出方程求解即可．
（3）本题考查一元一次方程得应用，设超市打折销售，根据原费用（折扣数）现在的费用，即可解题．
【详解】（1）解：由题知，购买1个足球和1个篮球，总费用140元，
第三次采购，购买8个足球和8个篮球在加2个篮球，根据（元），
，
第三次采购打了折扣，
故答案为：三．
（2）解：设每个足球的标价为元，则每个篮球的标价为元，
根据第二次采购可列式为：，
整理得，解得，
则每个篮球的标价为（元），
答：每个足球的标价为元，则每个篮球的标价为元．
（3）解：设超市打折销售，
原来的总费用为：（元），
根据题意得：，解得，
答：超市打8折销售．
27．数学思考：见解析；拓展探究：，证明见解析；问题解决：或
【分析】本题主要考查了平行线的性质与判定：
数学思考：如图所示，过点E作，则，由平行线的性质得到，则；
拓展探究：如图所示，过点E作，则，由平行线的性质得到，则；
问题解决：分当点E在线段上时，当点E在线段延长线上时，两种情况利用数学思考和拓展探究的结论求解即可．
【详解】解：数学思考：理由如下；如图所示，过点E作，
∵，
∴，
∴，
∴，即；
拓展探究：，证明如下：
如图所示，过点E作，
∵，
∴，
∴，
∴，即；
问题解决：如图所示，当点E在线段上时，由数学思考可得；
如图所示，当点E在线段延长线上时，由拓展探究可得；
综上所述，的度数为或．