06函数模型的应用-北京市2023-2024学年高一上学期期末数学专题练习（人教A版，2019新版）

这是一份06函数模型的应用-北京市2023-2024学年高一上学期期末数学专题练习（人教A版，2019新版），共19页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
一、单选题
1．（2024上·北京东城·高一统考期末）某品牌可降解塑料袋经自然降解后残留量y与时间t（单位：年）之间的关系为．其中为初始量，k为降解系数．已知该品牌塑料袋2年后残留量为初始量的．若该品牌塑料袋需要经过n年，使其残留量为初始量的，则n的值约为（ ）（参考数据：，）
A．20B．16C．12D．7
2．（2024上·北京通州·高一统考期末）国家标准对数视力表是由我国第一个眼科光学研究室的创办者缪天荣发明设计的，如图是5米测距下的标准对数视力表的一部分.图中左边一列数据为标准对数记录法记录的近似值L：4.0，4.1，4.2…对应右边一列数据为小数记录法记录的近似值V：0.1，0.12，0.15….已知标准对数记录法的数据L和小数记录法的数据V满足（K为常数）.某同学测得视力的小数记录法数据为0.6，则其标准对数记录法的数据约为（参考数据：，）（ ）
标准对数视力表
A．4.8B．4.9C．5.0D．5.1
3．（2024上·北京密云·高一统考期末）近年来，密云区生物多样性保护成效显著，四百多种野生鸟类在密云繁衍生息，近万候鸟变留鸟，鸟类科学家发现，两岁燕子的飞行速度可以表示为耗氧量的函数.若两岁燕子耗氧量达到40个单位时，其飞行速度为，则两岁燕子飞行速度为时，其耗氧量达到（ ）
A．80个单位B．120个单位C．160个单位D．320个单位
4．（2024上·北京朝阳·高一统考期末）在一定通风条件下，某会议室内的二氧化碳浓度c随时间t（单位：）的变化规律可以用函数模型近似表达．在该通风条件下测得当时此会议室内的二氧化碳浓度，如下表所示，用该模型推算当时c的值约为（ ）
A．B．C．D．
5．（2024上·北京顺义·高一统考期末）燕子每年秋天都要从北方飞向南方过冬.专家发现两岁燕子的飞行速度v（单位：）可以表示为，其中Q表示燕子耗氧量的单位数.某只两岁燕子耗氧量的单位数为时的飞行速度为，耗氧量的单位数为时的飞行速度为，若，则的值为（ ）
A．B．C．D．
6．（2024上·北京丰台·高一统考期末）荀子《劝学》中说：“不积跬步，无以至千里；不积小流，无以成江海.”学习是日积月累的过程，每天进步一点点，前进不止一小点.若甲、乙两同学当下的知识储备量均为a，甲同学每天的“进步”率和乙同学每天的“退步”率均为2%.n天后，甲同学的知识储备量为，乙同学的知识储备量为，则甲、乙的知识储备量之比为2时，需要经过的天数约为（ ）（参考数据：，，）
A．15B．18C．30D．35
7．（2024上·北京西城·高一统考期末）一种细胞的分裂速度（单位：个/秒）与其年龄（单位：岁）的关系可以用下面的分段函数来表示：其中，而且这种细胞从诞生到死亡，它的分裂速度变化是连续的．若这种细胞5岁和60岁的分裂速度相等，则（ ）
（参考数据：）
A．B．C．D．
8．（2023上·北京·高一北京市十一学校校考期末）函数的零点个数是（ ）
A．1B．2C．3D．4
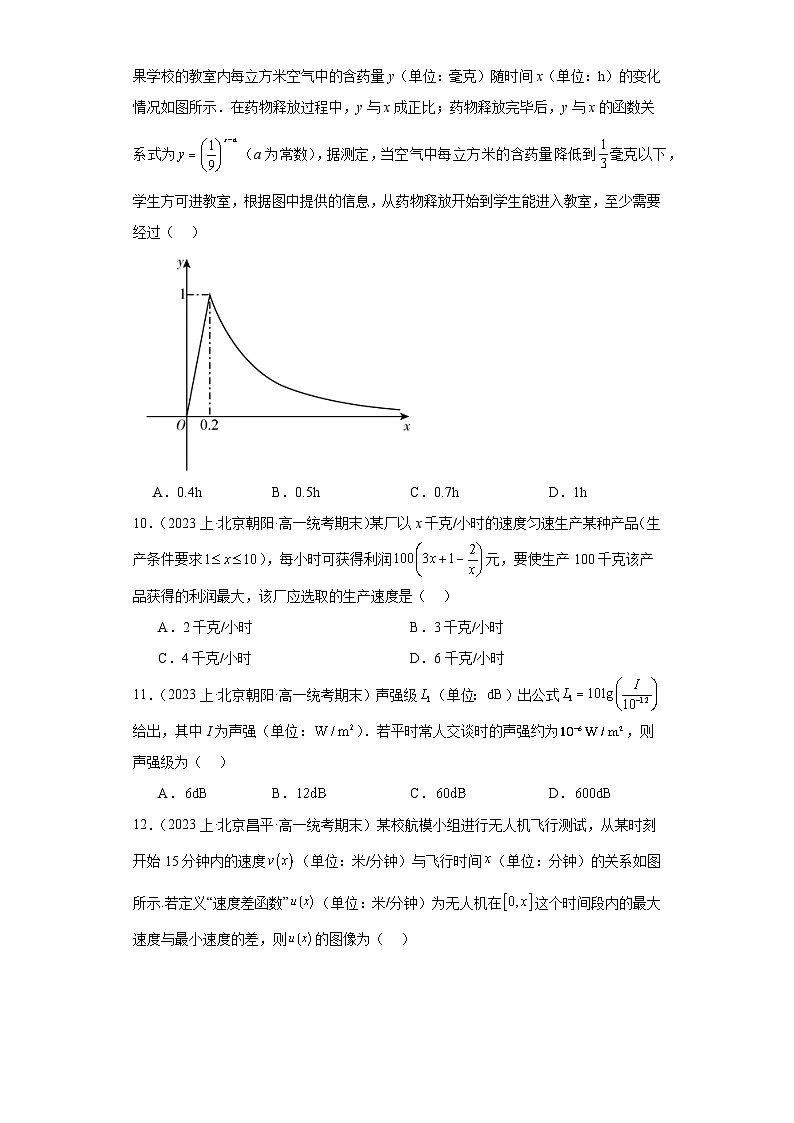
9．（2023上·北京平谷·高一统考期末）中医药在疫情防控中消毒防疫作用发挥有力，如果学校的教室内每立方米空气中的含药量y（单位：毫克）随时间x（单位：h）的变化情况如图所示．在药物释放过程中，y与x成正比；药物释放完毕后，y与x的函数关系式为（a为常数），据测定，当空气中每立方米的含药量降低到毫克以下，学生方可进教室，根据图中提供的信息，从药物释放开始到学生能进入教室，至少需要经过（ ）
A．0.4hB．0.5hC．0.7hD．1h
10．（2023上·北京朝阳·高一统考期末）某厂以x千克/小时的速度匀速生产某种产品（生产条件要求），每小时可获得利润元，要使生产100千克该产品获得的利润最大，该厂应选取的生产速度是（ ）
A．2千克/小时B．3千克/小时
C．4千克/小时D．6千克/小时
11．（2023上·北京朝阳·高一统考期末）声强级（单位：）出公式给出，其中I为声强（单位：）．若平时常人交谈时的声强约为，则声强级为（ ）
A．B．C．D．
12．（2023上·北京昌平·高一统考期末）某校航模小组进行无人机飞行测试，从某时刻开始15分钟内的速度（单位：米/分钟）与飞行时间（单位：分钟）的关系如图所示.若定义“速度差函数”（单位：米/分钟）为无人机在这个时间段内的最大速度与最小速度的差，则的图像为（ ）
A．B．
C．D．
二、填空题
13．（2023上·北京顺义·高一统考期末）A､B､C三个物体同时从同一点出发向同向而行，位移关于时间的函数关系式分别为，则下列结论中，所有正确结论的序号是 .
①当时，A总走在最前面；
②当时，C总走在最前面；
③当时，一定走在前面.
14．（2023上·北京海淀·高一统考期末）请阅读以下材料，并回答后面的问题：
材料1：人体成分主要由骨骼､肌肉､脂肪等组织及内脏组成，肌肉是最大的组织，且肌肉的密度相比脂肪而言要大很多.肌肉和脂肪在体重中占比个体差异较大，脂肪占体重的百分比（称为体脂率，记为）经常作为反映肥胖程度的一个重要指标，但是不易于测量.
材料2：体重指数BMI（BdyMassIndex的缩写）计算公式为：体重指数BMI为体重，单位：千克；为身高，单位：米），是衡量人体整体胖瘦程度的一个简单易得的重要指标.1997年，世界卫生组织经过大范围的调查研究后公布：BMI值在为正常；为超重；为肥胖.由于亚洲人与欧美人的体质有较大差异，国际肥胖特别工作组经调查研究后，于2000年提出了亚洲成年人BMI值在为正常.中国肥胖问题工作组基于中国人体质特征，于2003年提出中国成年人BMI值在为正常；为超重；为肥胖. 30岁的小智在今年的体检报告中，发现体质指数BMI值为，依照标准属于超重.因为小智平时还是很注意体育锻炼的，正常作息，且每周去健身房有大约2小时的健身运动，周末还经常会和朋友去打篮球，所以小智对自己超重感觉很困惑.
请你结合上述材料，从数学模型的视角，帮小智做一下分析（包括：是否需要担心？为什么？）： .
15．（2021上·北京通州·高一统考期末）果蔬批发市场批发某种水果，不少于千克时，批发价为每千克元，小王携带现金3000元到市场采购这种水果，并以此批发价买进，如果购买的水果为千克，小王付款后剩余现金为元，则与之间的函数关系为 ；的取值范围是 .
16．（2021上·北京西城·高一统考期末）某厂商为推销自己品牌的可乐，承诺在促销期内，可以用3个该品牌的可乐空罐换1罐可乐.对于此促销活动，有以下三个说法：
①如果购买10罐可乐，那么实际最多可以饮13罐可乐;
②欲饮用100罐可乐，至少需要购买67罐可乐：
③如果购买罐可乐，那么实际最多可饮用可乐的罐数.（其中表示不大于x的最大整数）
则所有正确说法的序号是 .
17．（2021上·北京·高一101中学校考期末）某地下车库在排气扇发生故障的情况下，测得空气中一氧化碳的含量达到了危险状态，经抢修后恢复正常．排气4分钟后测得车库内一氧化碳浓度为64ppm（ppm为浓度单位，1ppm表示百万分之一），经检验知，该地下车库一氧化碳浓度（ppm）与排气时间（分钟）之间存在函数关系（为常数）．求得 ；若空气中一氧化碳浓度不高于0.5ppm为正常，那么至少需要排气 分钟才能使这个地下车库中一氧化碳含量达到正常状态．
18．（2021上·北京丰台·高一统考期末）一种药在病人血液中的量保持在以上时才有疗效，而低于时病人就有危险.现给某病人的静脉注射了这种药，如果药在血液中以每小时20%的比例衰减，设经过x小时后，药在病人血液中的量为.
（1）y关于x的函数解析式为 ；
（2）要使病人没有危险，再次注射该药的时间不能超过 小时.(精确到0.1)(参考数据：，，，)
三、解答题
19．（2024上·北京昌平·高一统考期末）某旅行社不定期组成旅游团去风景区旅游，若旅游团人数在30或30以下（不低于20），则收取费用180元/人；若旅游团人数大于30，则给予如下优惠：每多1人，费用每人减少3元，直到达到满额50人为止（大客车限乘51人，含司机）．旅行社每次需支出成本费用3000元.
(1)若旅游团人数为40，求每人应交的费用；
(2)设旅游团人数为x时每人应交的费用为y元，求出y与x之间的关系式；
(3)求旅游团人数x为多少时，旅行社可获得的利润L最大.
20．（2024上·北京东城·高一统考期末）某地要建设一座购物中心，为了减少能源损耗，计划对其外墙建造可使用30年的隔热层，已知每厘米厚的隔热层的建造成本为9万元．该建筑物每年的能源消耗费用P（单位：万元）与隔热层厚度工（单位：cm）满足关系：（）．若不建隔热层，每年能源消耗费用为6万元．设S为隔热层建造费用与30年的能源消耗费用之和．
(1)求出S关于的函数解析式；
(2)若使隔热层建造费用与30年的能源消耗费用之和S控制在90万元以内，隔热层的厚度不能超过多少厘米？隔热层的厚度为整数）
21．（2024上·北京丰台·高一统考期末）2023年9月23日第十九届亚运会在杭州开幕，本届亚运会吉祥物是“琮琮”、“莲莲”、“宸宸”.某商家成套出售吉祥物挂件，通过对销售情况统计发现：在某个月内（按30天计），每套吉祥物挂件的日销售价格（单位：元）与第x天的函数关系满足（k为常数，且），日销售量（单位：套）与第x天的部分数据如下表所示：
设该月吉祥物挂件的日销售收入为（单位：元），已知第15天的日销售价格为32元.
(1)求k的值；
(2)根据上表中的数据，若用函数模型来描述该月日销售量与第x天的变化关系，求函数的解析式；
(3)利用（2）中的结论，求的最小值.
22．（2023上·北京昌平·高一统考期末）为了践行“节能减排，绿色低碳”的发展理念，某企业加大了对生活垃圾处理项目的研发力度.经测算，企业每月平均处理生活垃圾的增量y（单位：吨）与每月投入的研发费用（单位：万元）之间的函数关系式为.
(1)若要求每月平均处理生活垃圾的增量不低于100吨，则每月投入的研发费用应该在什么范围？
(2)当每月投入的研发费用为多少时，每月平均处理生活垃圾的增量达到最大值？最大值是多少？
t
0
5
10
c
x
15
20
25
30
650
645
650
655
参考答案：
1．B
【分析】由可得，再代入，求解即可.
【详解】根据题意可得，
则，，
则经过n年时，有，
即，则，
所以，
则.
故选：B.
2．A
【分析】利用公式结合对数运算法则计算函数关系式即可.
【详解】由题意可知，所以，
故，故A正确.
故选：A
3．C
【分析】结合题意结合对数运算求得，然后列方程，利用指对互化求解即可.
【详解】因为两岁燕子耗氧量达到40个单位时，其飞行速度为，
所以，所以，所以，
当两岁燕子飞行速度为时，，解得，所以，
即两岁燕子飞行速度为时，其耗氧量达到160个单位.
故选：C
4．C
【分析】根据题意知建立方程组分别求出，，从而可求解.
【详解】由题意得：当时，，
当时，，
当时，，
由得，
由得，
由得，所以，
由得，解得，
所以当时，，
故C正确.
故选：C.
5．D
【分析】利用公式，结合对数的运算性质进行求解即可.
【详解】因为，
所以
所以，
故选：D
6．B
【分析】根据题意列式，结合对数运算，即可求得答案.
【详解】由题意可设经过n天后甲、乙的知识储备量之比为2，
则，
则（天），
故选：B
7．B
【分析】根据题意得以及，解方程组即可求出.
【详解】由已知细胞5岁和60岁的分裂速度相等，即，
所以，整理得①，
又分裂速度变化是连续的，则，整理得，
所以，
解得
故选：B,
8．A
【分析】数形结合，结合指数函数和二次函数的变化趋势分析两函数交点情况，进而确定零点个数.
【详解】由，得，
令，，
在同一直角坐标系中画出两函数图象，如下：
当时，两图象由一个交点，
当时，函数上升趋势明显大于，故无交点，
所以两函数有一个交点，所以函数的零点个数是1.
故选：A
9．C
【分析】根据函数图象经过点，求出的值，然后利用指数函数的单调性解不等式即得.
【详解】由题意知，点在函数的图象上，
所以，
解得，
所以，
由，可得，
所以，
解得，
所以从药物释放开始，到学生回到教室至少需要经过的小时.
故选：C.
10．C
【分析】生产100千克该产品获得的利润为，令，由换元法求二次函数最大值即可.
【详解】由题意得，生产100千克该产品获得的利润为，，
令，，则，故当时，最大，此时.
故选：C
11．C
【分析】根据对数运算求得正确答案.
【详解】依题意.
故选：C
12．C
【分析】根据图像分析，即可得到答案
【详解】由题图知,当时, 无人机做匀加速运动,,“速度差函数”;
当时, 无人机做匀减速运动,速度从160开始下降,一直降到80,“速度差函数”;
当时, 无人机做匀减速运动, 从80开始下降, ,“速度差函数”;
当时无人机做匀加速运动,“速度差函数”.
所以函数在和两个区间上都是常数.
故选：C
13．①②
【分析】画出三函数的图象，结合三种类型函数的增长速度，数形结合得到结论.
【详解】在同一坐标系内画出的函数图象，
当时，指数函数的增长速度>幂函数的增长速度>对数函数的增长速度，
当时，，故当时，A总走在最前面，①正确；
当时，由图象可知：C总走在最前面，②正确；
当时，，
当时，，
由于幂函数的增长速度>对数函数的增长速度，
故时，B走在C前面，
当时，走在后面，③错误.
故答案为：①②
14．答案见解析
【分析】根据材料结合条件分析即得.
【详解】因为小智平时注意锻炼，肌肉占比相对高，意味着身体密度大，相同体型和身高情况下，BMI值与密度成正比（或者说，体重更大），
所以他的BMI值就会偏高，如果小智体型基本正常（或者说身高远高于中国人平均值），就不必担心.
故答案为：如果小智体型基本正常（或者说身高远高于中国人平均值），他的BMI值就会偏高，就不必担心，因为小智平时注意锻炼，肌肉占比相对高，意味着身体密度大，相同体型和身高情况下，BMI值与密度成正比（或者说，体重更大）.
15．
【解析】根据题意，直接列式，根据题意求的最小值和最大值，得到的取值范围.
【详解】由题意可知函数关系式是，
由题意可知最少买千克，最多买千克，所以函数的定义域是.
故答案为：；
16．②③.
【解析】①罐可乐有个可乐空罐，第一次可换罐可乐还剩个空罐，第二次可换罐可乐还剩个空罐，由此算出最多可饮用的可乐罐数；
②：先分析购买罐可乐的情况，再分析购买罐可乐的情况，由此确定出至少需要购买的可乐罐数；
③：先分析购买到罐可乐分别可饮用多少罐可乐以及剩余空罐数，然后得到规律，再分奇偶罐数对所得到的规律进行整理，由此计算出的结果.
【详解】①：购买罐可乐时，第一次可换罐还剩个空罐，第二次可换罐还剩个空罐，所以最多可饮用罐可乐，故错误；
②：购买罐时，第一次可换罐可乐，第二次可换罐可乐还剩个空罐，
第三次可换罐可乐还剩个空罐，第四次可换罐可乐还剩个空罐，所以一共可饮用罐；
购买罐时，第一次可换罐可乐还剩个空罐，第二次可换瓶可乐还剩个空罐，
第三次可换罐可乐，第四次可换罐可乐还剩个空罐，所以一共可饮用罐；
所以至少需要购买罐可乐，故正确；
③：购买到罐可乐分别可饮用可乐罐数以及剩余空罐数如下表所示：
由表可知如下规律：
（1）当购买的可乐罐数为奇数时，此时剩余空罐数为，当购买的可乐罐数为偶数时，此时剩余的空罐数为；
（2）实际饮用数不是的倍数；
（3）每多买罐可乐，可多饮用罐可乐，
（4）实际饮用的可乐罐数要比购买的可乐罐数的倍少或；
设购买了罐可乐，实际可饮用的可乐罐数为，
所以，即，即，
又因为可看作，即不大于的最大整数，所以成立，故正确；
故答案为：②③.
【点睛】关键点点睛：解答本题时，一方面需要通过具体购买的可乐罐数去分析实际饮用的可乐罐数，另一方面需要对实际的购买情况进行归纳，由此得到购买的可乐罐数与实际饮用的可乐罐数的关系，从而解决问题.
17． ． ．
【解析】由已知得当时，，代入可求得答案；根据题意构造不等式，解之即可．
【详解】由已知得当时，，所以，解得，
所以，所以，解得，
故答案为：；．
18． 7.2
【解析】（1）利用指数函数模型求得y关于x的函数解析式；
（2）根据题意利用指数函数的单调性列不等式，求得再次注射该药的时间不能超过的时间.
【详解】（1）由题意，该种药在血液中以每小时20%的比例衰减，给病人注射了该药，经过x小时后，药在病人血液中的量为.
即y关于x的函数解析式为
（2）该药在病人血液中的量保持在以上时才有疗效，低于时病人就有危险，
令，即
又，且指数函数为减函数，
所以要使病人没有危险，再次注射该药的时间不能超过7.2小时.
19．(1)150元；
(2)；
(3)45.
【分析】（1）根据题意计算即可；
（2）根据自变量的取值范围，分或列出函数解析式即可；
（3）利用题中的函数解析式，结合自变量的取值范围和配方法，分段求最值，即可得到结论．
【详解】（1）若旅游团人数为40，每人应交的费用为：元；
（2）当时，，
当时，，
即；
（3）当时，，
当时，，
即.
当时，中随的增大而增大，
所以时，，
当时，，
即时，.
所以当旅游团人数为时，旅行社可获得的利润L最大.
20．(1),
(2)6
【分析】（1）利于给定条件，求出的值，进而可得能源消耗费用与隔热层建造成本之和.
（2）根据条件建立不等式，解出后进一步分析即可.
【详解】（1）依题意，当时，，所以，
所以，，
则（万元），.
（2）若，
不等式化为，
解得
又，
所以隔热层的厚度不能超过6厘米.
21．(1)
(2)， ，.
(3)20280元
【分析】（1）将代入，即可求得答案；
（2）结合表格中数据确定m的值，再解方程，即可求得答案；
（3）求出的表达式，讨论x的取值范围，结合函数单调性以及基本不等式，即可求得答案.
【详解】（1）由题意得，所以，解得.
（2）根据表中数据以及，可知，当时，取得最小值；
根据表中数据可得，，
由，得，，，
所以，其中，.
（3）由（1）（2）可知，，，
当时，，
可知在时随着x的增大而减小，
所以当时的最小值为；
当时，，
因为，当且仅当时，等号成立，
所以当时的最小值为，
综上所述，当时，该月日销售收入的最小值为20280元.
22．(1)每月投入的研发费用的范围是万元
(2)每月投入的研发费用为20万元时，每月平均处理生活垃圾的增量达到最大值，最大值是120吨.
【分析】（1）根据题意得到，然后解不等式即可求解；
（2）利用基本不等式即可求解
【详解】（1）根据题意，，
因为
所以不等式转化为化简可得，解得
所以每月投入的研发费用的范围是万元
（2）因为，所以，
因为，当且仅当，即时，取等号，
所以当且仅当时，取得最大值.
所以每月投入的研发费用为20万元时，每月平均处理生活垃圾的增量达到最大值，最大值是120吨.
购买数
饮用数
剩余空罐数