河南省信阳市罗山县2023-2024学年八年级上学期期末数学试卷（含解析）

这是一份河南省信阳市罗山县2023-2024学年八年级上学期期末数学试卷（含解析），共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.中国汉字文化源远流长，篆书是汉字古代书体之一下列篆体字“大”“美”“中”“原”中，不是轴对称图形的是( )
A. B. C. D.
2.下列运算正确的是
( )
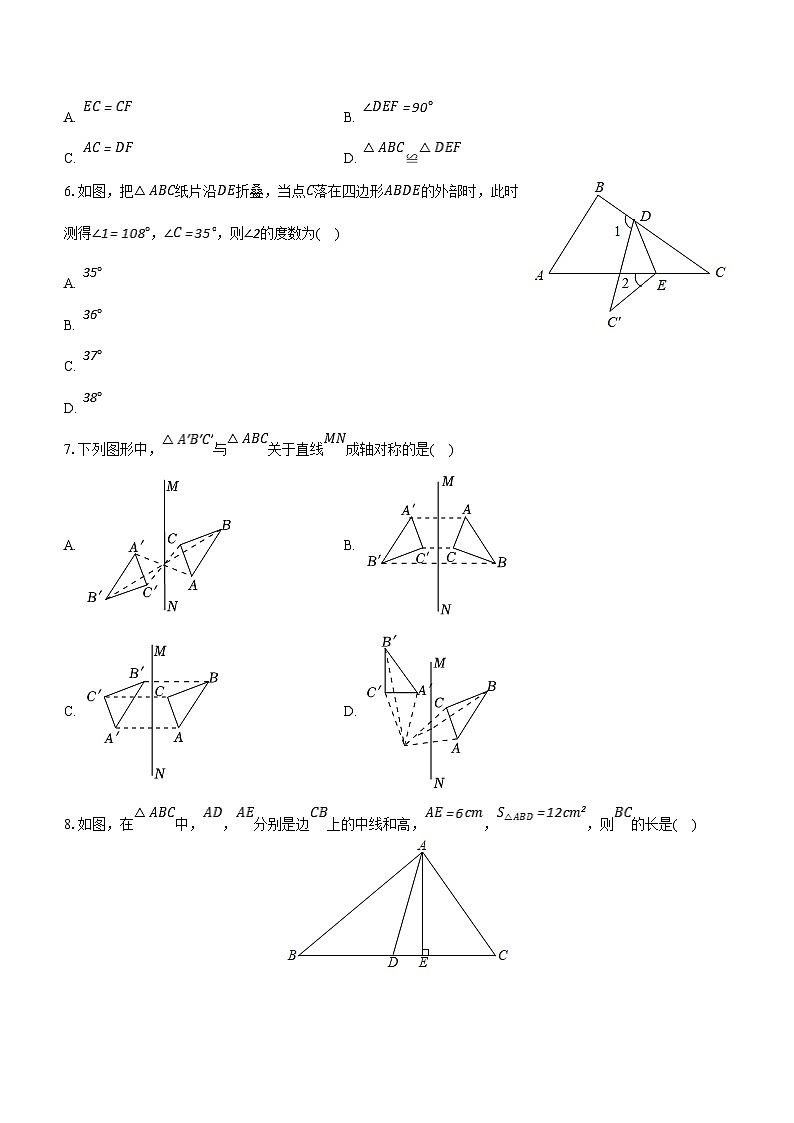
A. B. C. D.
3.下列因式分解错误的是( )
A.
B.
C.
D.
4.如图，已知，以点为圆心，任意长度为半径画弧，分别交，于点，，再以点为圆心，的长为半径画弧，交弧于点，画射线若，则的度数为( )
A. B. C. D.
5.如图，沿所在直线向右平移得到，则下列结论中，不一定正确的是( )
A. B.
C. D. ≌
6.如图，把纸片沿折叠，当点落在四边形的外部时，此时测得，，则的度数为( )
A.
B.
C.
D.
7.下列图形中，与关于直线成轴对称的是( )
A. B.
C. D.
8.如图，在中，，分别是边上的中线和高，，，则的长是( )
A. B. C. D.
9.要使分式有意义，则实数应满足的条件是( )
A. B. 或
C. 且D. 且且
10.定义运算“”：，若，则的值为( )
A. B. C. D. 或
二、填空题：本题共5小题，每小题3分，共15分。
11.点关于轴对称的点的坐标为______．
12.因式分解： ______．
13.如图是可调躺椅示意图数据如图，与的交点为，且，，保持不变为了舒适，需调整的大小，使，则图中应减少______度
14.已知分式，当时，分式的值为，当时，分式无意义，则 ______．
15.如图，是的外角的角平分线，，于点，若，，则的长为______．
三、解答题：本题共8小题，共75分。解答应写出文字说明，证明过程或演算步骤。
16.本小题分
计算：；
运用公式进行简便计算：．
17.本小题分
计算：；
解分式方程：．
18.本小题分
如图所示，在中，是高，、是角平分线，它们相交于点，，，求、的度数．
19.本小题分
如果一个正整数能表示为两个连续的偶数的平方差，那么称这个正整数为“神秘数”如果，，，因此，，都是“神秘数”．
和这两个数是“神秘数”吗？为什么？
设两个连续偶数为和其中取非负整数，由这两个连续偶数构造的“神秘数”是的倍数吗？为什么？
两个连续的奇数的平方差取正整数是“神秘数”吗？为什么？
20.本小题分
小丽与爸妈在公园里荡秋千，如图，小丽坐在秋千的起始位置处，与地面垂直，两脚在地面上用力一蹬，妈妈在距地面高的处接住她后用力一推，爸爸在处接住她若妈妈与爸爸到的水平距离、分别为和，．
与全等吗？请说明理由；
爸爸在距离地面多高的地方接住小丽的？
21.本小题分
现有一张纸片，点、分别是边上两点，若沿直线折叠．
研究：如果折成图的形状，使点落在上，则与的数量关系是______．
研究：如果折成图的形状，猜想与的数量关系是______；
研究：如果折成图的形状，猜想、和的数量关系，并说明理由．
22.本小题分
金师傅近期准备换车，看中了价格相同的两款国产车．
用含的代数式表示新能源车的每千米行驶费用．
若燃油车的每千米行驶费用比新能源车多元．
分别求出这两款车的每千米行驶费用．
若燃油车和新能源车每年的其它费用分别为元和元．问：每年行驶里程为多少千米时，买新能源车的年费用更低？年费用年行驶费用年其它费用
23.本小题分
如图，点在线段上点不与，重合，分别以，为边在同侧作等边三角形和等边三角形，连接，交于点．
观察猜想：
与的数量关系为______．
的度数为______；
数学思考：
如图，当点在线段外时，中的结论，是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明．
拓展应用：
如图，点为四边形内一点，且满足，，对角线，交于点，，则四边形的面积为______．
答案和解析
1.【答案】
【解析】解：、是轴对称图形，不合题意；
B、是轴对称图形，不符合题意；
C、是轴对称图形，不合题意；
D、不是轴对称图形，符合题意；
故选：．
根据关于某条直线对称的图形叫轴对称图形，进而判断得出即可．
此题主要考查了轴对称图形，轴对称图形的关键是寻找对称轴，对称轴可使图形两部分折叠后重合．
2.【答案】
【解析】【分析】
本题考查合并同类项、同底数幂的乘法、幂的乘方与积的乘方，熟练掌握运算性质和法则是解题的关键．
根据同底数幂相乘，底数不变指数相加；积的乘方，等于把积的每一个因式分别乘方再把所得的幂相乘；幂的乘方，底数不变指数相乘；以及合并同类项法则对各选项分析判断即可得解．
【解答】
解：，故本选项错误；
B.，故本选项正确；
C.，故本选项错误；
D.，故本选项错误．
故选：．
3.【答案】
【解析】解：、正确，故本选项错误；
B、，故本选项正确；
C、正确，故本选项错误；
D、正确，故本选项错误．
故选：．
根据提公因式法分解因式和公式法分解因式对各选项分析判断后利用排除法求解．
本题考查了用提公因式法和公式法进行因式分解，一个多项式有公因式首先提取公因式，然后再用其他方法进行因式分解，同时因式分解要彻底，直到不能分解为止．
4.【答案】
【解析】解；根据作图过程可知：，，
在和中，
，
≌，
，
，
则的度数为．
故选：．
根据作图过程可得，，利用证明≌，即可得结果．
本题考查了全等三角形的判定与性质，作图复杂作图，解决本题的关键是掌握全等三角形的判定．
5.【答案】
【解析】解：由平移的性质得：，和不一定相等，
故A符合题意；
由平移的性质得到≌，
，，
故B、、不符合题意．
故选：．
把一个图形整体沿某一直线方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同，新图形中的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点．连接各组对应点的线段平行且相等，由此即可判断．
本题考查平移的性质，全等三角形的性质，关键是掌握平移的性质．
6.【答案】
【解析】解：如图，设与交于点，
，
，
，，
，
，
．
故选：．
根据折叠性质得出，根据三角形外角性质得出，．
本题考查了多边形的内角与外角，熟记多边形的内角和定理及三角形的外角定理是解题的关键．
7.【答案】
【解析】解：根据轴对称的性质，结合四个选项，只有选项中对应点的连线被对称轴垂直平分，所以是符合要求的．
故选：．
认真观察各选项给出的图形，根据轴对称的性质，对称轴垂直平分线对应点的连线进行判断．
本题考查轴对称的性质；应用对应点的连线与对称轴的位置关系是互相垂直，对应点所连的线段被对称轴垂直平分解题是正确解答本题的关键．
8.【答案】
【解析】解：为边上的中线，
，
即，
又，
解得：，
故选：．
由为边上的中线可得，再根据三角形的面积计算公式，可解出的长．
本题考查了三角形中线的性质，三角形的面积，熟知三角形中线的性质和三角形的面积计算公式是关键．
9.【答案】
【解析】解：由题意得：，
则且，
故选：．
根据分式的分母不等于零列出不等式，解不等式即可．
本题考查的是分式有意义的条件，熟记分式的分母不等于零是解题的关键．
10.【答案】
【解析】【分析】
根据定义运算的意义，当、时分别列式求出．
本题考查了解分式方程，理解新定义的运算方法是解决本题的关键．
【解答】
解：当时，
因为，
所以，
解得．
经检验，符合题意，是分式方程的解．
当时，
因为，
所以．
解得．
经检验，符合题意，是分式方程的解．
故选：．
11.【答案】
【解析】解：关于轴对称的点的坐标为，
故答案为：．
利用平面内两点关于轴对称时：横坐标不变，纵坐标互为相反数，进行求解．
本题考查了关于轴对称的点的坐标，解决本题的关键是掌握好对称点的坐标规律：关于轴对称的点，横坐标相同，纵坐标互为相反数；关于轴对称的点，纵坐标相同，横坐标互为相反数；关于原点对称的点，横坐标与纵坐标都互为相反数．
12.【答案】
【解析】解：原式，
故答案为：．
先提取公因式，再利用完全平方公式即可．
本题考查提公因式法、公式法分解因式，掌握完全平方公式的结构特征是正确应用的前提．
13.【答案】
【解析】解：延长，交于点，如图：
，
．
，
．
，，
．
而图中，
应减少．
故答案为：．
延长，交于点，依据三角形的内角和定理可求，根据对顶角相等可得，再由三角形内角和定理的推论得到的度数；利用，和三角形的外角的性质可得的度数，从而得出结论．
本题主要考查了三角形的外角的性质，三角形的内角和定理．熟练使用上述定理是解题的关键．
14.【答案】
【解析】解：根据题意得：，
解得：，
所以．
故答案为：．
根据题意列出关于、的方程，解方程求出、的值，代入代数式求出结果即可．
本题考查分式，掌握分式有意义条件和分式为零的条件是解题的关键．
15.【答案】
【解析】解：如图，过点作于，
是的角平分线，
，
在和中，
，
≌，
，
在和中，
，
≌，
，
，
，
，
，
，，
，
解得．
故答案为．
过点作于，根据角平分线上的点到角的两边的距离相等可得，再利用“”证明和全等，和全等，根据全等三角形对应边相等可得，即可解决问题；
本题考查了角平分线的性质，全等三角形的判定与性质，作辅助线构造出两对全等三角形是解题的关键，也是本题的难点．
16.【答案】解：

；




．
【解析】先计算立方根、绝对值和二次根式，再计算加减；
将该算式变形后运用完全平方公式进行求解．
此题考查了实数混合运算的能力，关键是能确定准确的运算顺序，并能进行正确的计算．
17.【答案】解：原式

；
原方程去分母得：，
整理得：，
解得：，
检验：将代入得，
故原方程的解为．
【解析】利用积的乘方法则，单项式乘多项式法则及多项式除以单项式法则计算即可；
利用解分式方程的步骤解方程即可．
本题考查分式的混合运算及解分式方程，熟练掌握相关运算法则及解方程的方法是解题的关键．
18.【答案】解：，
，
，
，
，，
，
是的平分线，
，
是的角平分线，
，
．
【解析】因为是高，所以，又因为，所以度数可求；因为，，所以，，是的角平分线，则，故的度数可求．
本题考查了同学们利用角平分线的定义解决问题的能力，有利于培养同学们的发散思维能力．
19.【答案】解：，，
是“神秘数”；是“神秘数”；
两个连续偶数构成的“神秘数”是的倍数．
理由如下：
，
两个连续偶数构成的“神秘数”是的倍数，
是奇数，
它是的倍数，不是的倍数；
设两个连续的奇数为：，，则
，
此数是的倍数，而由知“神秘数”是的倍数，但不是的倍数，
所以两个连续的奇数的平方差不是神秘数．
【解析】根据“神秘数”的定义，只需看能否把和这两个数写成两个连续偶数的平方差即可判断；
运用平方差公式进行计算，进而判断即可；
运用平方差公式进行计算，进而判断即可．
此题考查了因式分解的实际运用，掌握平方差公式，理解新定义的意义是解题关键．
20.【答案】解：与全等．
理由如下：
由题意可知，，
，
．
，
在和中，
，
≌；
≌，
，，
、分别为和，
，，
，
妈妈在距地面高的处，即，

，
答：爸爸是在距离地面的地方接住小丽的．
【解析】由直角三角形的性质得出，根据可证明≌；
由全等三角形的性质得出，，求出的长则可得出答案．
本题考查了全等三角形的判定与性质，直角三角形的性质，证明≌是解题的关键．
21.【答案】
；
如图，，理由是：
，，
，
，
，
．

【解析】解：如图，，理由是：
由折叠得：，
，
；
故答案为：；
如图，猜想：，理由是：
由折叠得：，，
，
，
；
故答案为：；
见答案．
【分析】
根据折叠的性质和三角形外角的性质得出结论；
先根据折叠得：，，由两个平角和得：等于与四个折叠角的差，化简得结果；
利用两次外角的性质得出结论．
本题是折叠变换问题，思路分两类：一类是利用外角的性质得结论；一类是利用平角定义和多边形内角和相结合得结论；字母书写要细心，角度比较复杂，是易错题．
22.【答案】解：由表格可得，
新能源车的每千米行驶费用为：元，
即新能源车的每千米行驶费用为元；
燃油车的每千米行驶费用比新能源车多元，
，
解得，
经检验，是原分式方程的解，
，，
答：燃油车的每千米行驶费用为元，新能源车的每千米行驶费用为元；
设每年行驶里程为，
由题意得：，
解得，
答：当每年行驶里程大于时，买新能源车的年费用更低．
【解析】根据表中的信息，可以计算出新能源车的每千米行驶费用；
根据燃油车的每千米行驶费用比新能源车多元和表中的信息，可以列出相应的分式方程，然后求解即可，注意分式方程要检验；
根据题意，可以列出相应的不等式，然后求解即可．
本题考查分式方程的应用、一元一次不等式的应用、列代数式，解答本题的关键是明确题意，列出相应的分式方程和不等式．
23.【答案】
【解析】解：设交于点．
，都是等边三角形，
，，，
，
在和中，
，
≌，
．
故答案为：；
≌，
，
，
，即．
故答案为：；
结论仍然成立．
理由：设交于点．
，都是等边三角形，
，，，
在和中，
，
≌，
，，
，
，
即；
设交于点．
，都是等腰直角三角形，
，，，
，
≌，
，．
，
，
，
．
故答案为：．
根据等边三角形的性质可得到，，，进一步得到，再证明≌，可得结论；
根据全等三角形的性质可得，再结合求出的度数；
结论不变，证明方法类似；
证明，．
本题属于三角形综合题，考查了等边三角形的性质，等腰直角三角形的性质，全等三角形的判定和性质等知识，解题的关键是正确寻找全等三角形解决问题，属于中考常考题型．
燃油车
油箱容积：升
油价：元升
续航里程：千米
每千米行驶费用：元
新能源车
电池电量：千瓦时
电价：元千瓦时
续航里程：千米
每千米行驶费用：_____元