河南省漯河市高新区2023-2024学年九年级上学期期末数学试题

这是一份河南省漯河市高新区2023-2024学年九年级上学期期末数学试题，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
注意：本试卷分试题卷和答题卡两部分。考试时间100分钟，满分120分。考生应首先阅读试题卷及答题卡上的相关信息，然后在答题卡上作答，在试题卷上作答无效。交卷时只交答题卡。
一、选择题（每小题3分，共30分）
1．2024的相反数是（ ）
A． B． C．2024 D．
2．小聪把“爱学习，勤思考”六个字分别写在一个正方体的六个面上，这个正方体的展开图如图所示，则“勤”所在面的对面上的字是（ ）
A．“爱” B．“勤” C．“思” D．“考”
3．原子的质量如此小，无论书写、记忆、还是使用都极不方便．为方便应用，以一种碳原子质量的（即）为标准，其他原子的质量跟它相比较所得到的比值，称为相对原子质量．若一个碳原子的质量是，则该碳的相对原子质量为（ ）
A．12 B． C． D．
4．如图，水面AB与水杯下沿CD平行，光线EF从水中射向空气时发生折射，折射光线为FH，点G在射线EF上，己知，则等于（ ）
A． B． C． D．
5．小军同学将相同体积的水分别倒入底面半径不同的圆柱形量筒中，并记录数据如下表（其中S表示量筒底面积，h表示水面高度），当h=6时，对应的量筒底面积为（ ）
A．35 B．40 C．45 D．50
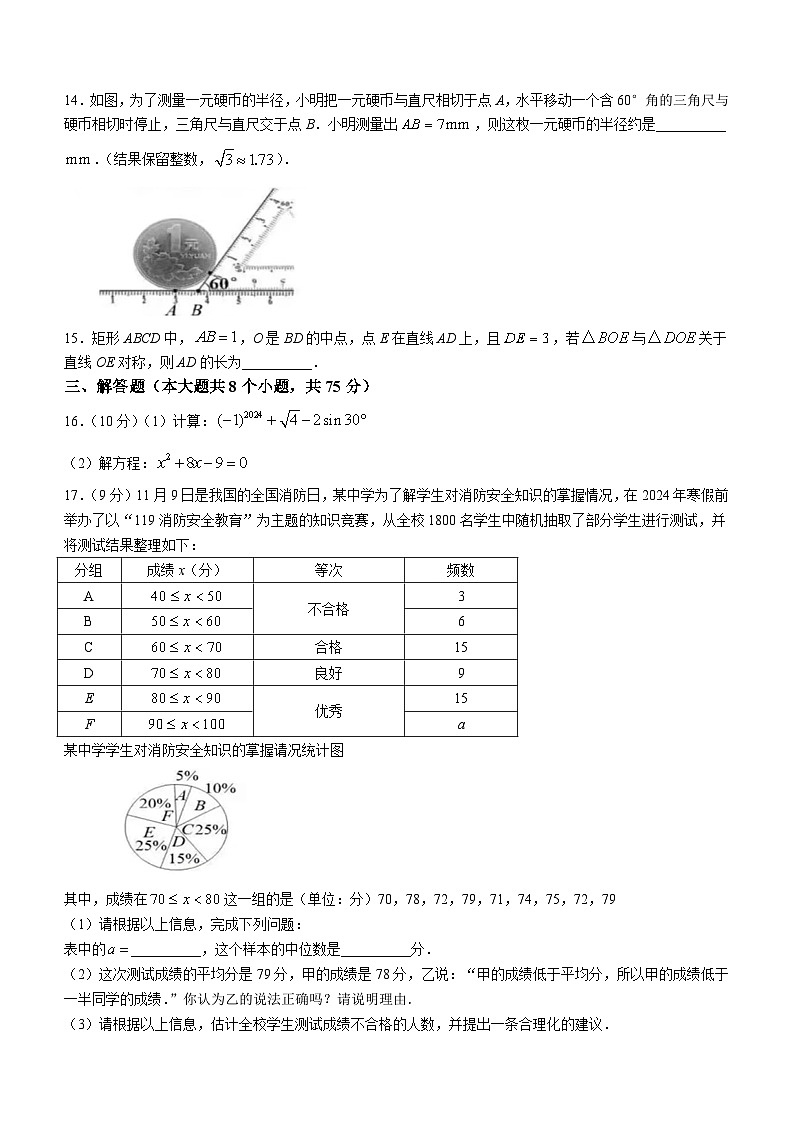
6．如图，点A，B，C在上，若，则的度数为（ ）
A． B． C． D．
7．关于x的一元二次方程的根的情况是（ ）
A．没有实数根 B．有两个相等的实数根
C．有两个不相等的实数根 D．实数根的个数与a的取值有关
8．如图，小强自制了一个小孔成像的装置，其中纸筒的长度为，他准备了一支长为的蜡烛，想要得到高度为的像，蜡烛应放在距离纸筒点O处（ ）的地方．
A． B． C． D．
9．己知抛物线，对称轴是直线，若点都在该抛物线的图象上，则a，b，c的大小关系为（ ）
A． B． C． D．
10．如图①，在正方形ABCD中，点E为DC边的中点，点P为线段BE上的一个动点．设，图②是点P运动时y随x变化的关系图象，则正方形的周长为（ ）
图① 图②
A． B．8 C． D．10
二、填空题（每小题3分，共15分）
11．请写出一个开口向上的二次函数表达式：____________________．
12．上体育课立定时，身高1.8米的小强落在地上的影子，与身高1.5米的小丽落在地上的影子的比值为__________．
13．河南省第14届运动会于2023年8月18日至8月28日在洛阳成功举办．大会共设青少年竞技组、学生组和社会组三个组．小亮和小明都是志愿者，他们被随机分配到这三个组的可能性相同．则小亮和小明被分配到同一组做志愿者的概率为__________．
14．如图，为了测量一元硬币的半径，小明把一元硬币与直尺相切于点A，水平移动一个含60°角的三角尺与硬币相切时停止，三角尺与直尺交于点B．小明测量出，则这枚一元硬币的半径约是__________．（结果保留整数，）．
15．矩形ABCD中，，O是BD的中点，点E在直线AD上，且，若与关于直线OE对称，则AD的长为__________．
三、解答题（本大题共8个小题，共75分）
16．（10分）（1）计算：
（2）解方程：
17．（9分）11月9日是我国的全国消防日，某中学为了解学生对消防安全知识的掌握情况，在2024年寒假前举办了以“119消防安全教育”为主题的知识竞赛，从全校1800名学生中随机抽取了部分学生进行测试，并将测试结果整理如下：
某中学学生对消防安全知识的掌握请况统计图
其中，成绩在这一组的是（单位：分）70，78，72，79，71，74，75，72，79
（1）请根据以上信息，完成下列问题：
表中的__________，这个样本的中位数是__________分．
（2）这次测试成绩的平均分是79分，甲的成绩是78分，乙说：“甲的成绩低于平均分，所以甲的成绩低于一半同学的成绩．”你认为乙的说法正确吗？请说明理由．
（3）请根据以上信息，估计全校学生测试成绩不合格的人数，并提出一条合理化的建议．
8．（9分）如图，在矩形ABCD中，，连接AC．
（1）请用无刻度的直尺和圆规作线段AC的垂直平分线，使其分别与AD，AC，BC交于点E，O，F（保留作图痕迹，不写作法）
（2）小明想用九年级三角形相似或三角函数的知识求线段EF的长，请你帮他完成求解过程．
19．（9分）如图，反比例函数的图象经过点，以点O为圆心，OA长为半径画弧，交x轴正半轴于点B，以O、A、B为顶点作菱形OACB，且．
（1）求反比例函数的表达式；
（2）求图中阴影部分的面积．
20．（9分）郑北大桥横跨亚洲最大铁路编组站，该桥为独塔双索面钢混结合梁斜拉桥，是国内同类型桥中桥面最宽的结合梁斜拉桥．某数学“综合与实践”小组的同学把“测量郑北大桥的某组斜拉索最高点到桥面的距离作为一项课题活动，进行了探究，具体过程如下：
【方案设计】如图，分别在A，B两点放置测角仪，测得和的度数，并量出AB的距离，即可解决问题：
【数据收集】米，测角仪AD和BE的高度为1.5米；
【问题解决】求郑北大桥某组斜拉索最高点C到桥面AB的距离．（结果保留整数．参考数据：，，）
21．（9分）河南胡辣汤制作技艺入选国家级非物质文化遗产代表性项目．得益于发达的网络销售模式，这种特色美食逐渐走出河南，畅销全国．某淘宝批发网店通过市场调研发现（整箱售卖）：若每箱胡辣汤料的利润为50元时，则平均每月可卖600箱：不考虑其他因素，每箱降价1元，平均每月就可以多卖20箱．为了尽快清库存，该网店决定采取适当的降价措施．
（1）若该淘宝店销售胡辣汤料的一个月总利润是31500元，则该网店每箱降价多少元？设每箱降价x元，那么每箱的销售利润为__________元，则每月销售量为__________箱．请你列出方程求解．
（2）该淘宝店想一个月的销售总利润达到33000元，请你通过计算说明是否能够达到；若不能达到，则一个月可达到的最大总利润为多少？
22．（10分）如图①，排球场长为，宽为，网高为．某校排球队员站在底线O点处向正前方发球，球从点O的正上方的C点发出，运动路线是抛物线的一部分（如图②），当球运动到最高点A处时，高度为，即，这时水平距离．以直线OB为x轴，直线OC为y轴，建立平面直角坐标系．
图① 图②
（1）求球运动的高度y（m）与水平距离x（m）之间的函数关系式（不必写出x的取值范围）
（2）根据比赛规则，发球过网，使其落在对方区域的地面上且不出界即为有效发球．请判断这次发球是否为有效发球（即能否过网？是否出界？），并说明理由．
23．（10分）在一节数学课上，张老师提出了这样一个问题：“如图1，在等腰直角三角形ABC中，，D是边BC上一动点（不与B重合），，DE交AB于点F．猜想线段BE，DF之间的数量关系并说明理由．”小聪和同桌小明讨论后，仍不得其解．张老师给出提示：数学中常通过把一个问题特殊化来找到解题思路．两个人茅塞顿开，于是进行了如下讨论，请仔细阅读，并完成相应的任务．
图1
小聪：己知点D是动点，因此可以将点D移动到一个特殊的位置．当点D与点C重合时，如图2所示．此时可以分别延长BE，CA交于点H，如图3所示，可证明，进而得出线段BE，DF之间的数量关系．
图2 图3 图4
小明：对于图2，过点F分别作BE，AC的平行线，交边BC于点M，N，如图4所示，可证明，进而得出线段BE，DF之间的数量关系．
（1）任务一：
如图2，判断线段BE，DF之间的数量关系：并在小聪与小明的方法中选择一种，写出详细的证明过程．
（2）任务二：
如图1，请直接猜想BE，DF之间的数量关系为__________．
（3）任务三：
如图1，若，当是直角三角形时，直接写出BD的长（用含a的代数式表示）．
九年级数学参考答案
一、选择题（每小题3分，共30分）
1．B 2．D 3．A 4．A 5．B 6．C 7．C 8．B 9．D 10．A
二、填空题（每小题3分，共15分）
11．（不唯一） 12． 13． 14．12 15．或
三、解答题（本大题共7个小题，共75分）
16．（10分）（1）原式． （5分）
（2）由，得或．
或． （10分）
17．（9分）
（1）12，76.5 （2分）
（2）乙的说法不正确． （3分）
理由：甲的成绩78分高于中位数76.5分，
∴甲的成绩不可能低于一半学生的成绩． （5分）
（3）全校学生测试成绩不合格的人数为：
名． （7分）
建议：学校应加大宣传力度，让学生都能掌握“消防安全”的相关知识． （9分）
18．（9分）（1）
（4分）
（2）在矩形ABCD中，，
在中，
， （6分）
，即 （8分）
同理 （9分）
19．（9分）（1）过A作于点D，
在中，，
反比例函数的图象经过点
，即，
反比例函数的表达式为 （5分）
（2）在菱形AOBC中．
（9分）
20．（8分）（1）过点C作，并延长CG交AB于点H
由题意得：，
设，则 （2分）
在中，
（4分）
在中，
（6分）
郑北大桥某组斜拉索最高点C到桥面AB的距离约为150米 （9分）
21．（9分）（1） （2分）
解：根据题意，可列方程
解得 （4分）
因为尽快清库存应舍去，
答：该网店每箱降价15元，则每月总利润是31500元 （5分）
（2）该淘宝店一个月的销售总利润不能达到33000元．
理由：设每箱降价x元时，每月的总利润为y元．根据题意得 （7分）
当时，y有最大值，最大值为32000，
该淘宝店一个月的销售总利润不能达到33000元，最大总利润为32000元． （9分）
22．（10分）（1）解：设y与x的函数关系式为 （1分）
由题可知：点为函数的顶点
（3分）
将点代入，得
与x的函数关系式为
（5分）
（2）这次发球为有效发球． （6分）
当时，
球可以过网． （8分）
令，则，解得
由题可知（舍），
（或当时，）
球没有出界
故这次发球为有效发球． （10分）
23．（10分）（1） （1分）
小聪：为等腰直角三角形，
．
又，
．
（3分）
，
．
又．
又． （6分）
小明：．
，
．
又．
（3分）
．
又．
又，
．
易证为等腰直角三角形
（6分）
（2）．．．．．．（8分）
（3）或． （10分）S（单位：）
20
30
60
80
h（单位：）
12
8
6
4
3
分组
成绩x（分）
等次
频数
A
不合格
3
B
6
C
合格
15
D
良好
9
E
优秀
15
F
a