2024年高考数学重难点突破讲义:学案 第4讲 立体几何中的计算问题——距离
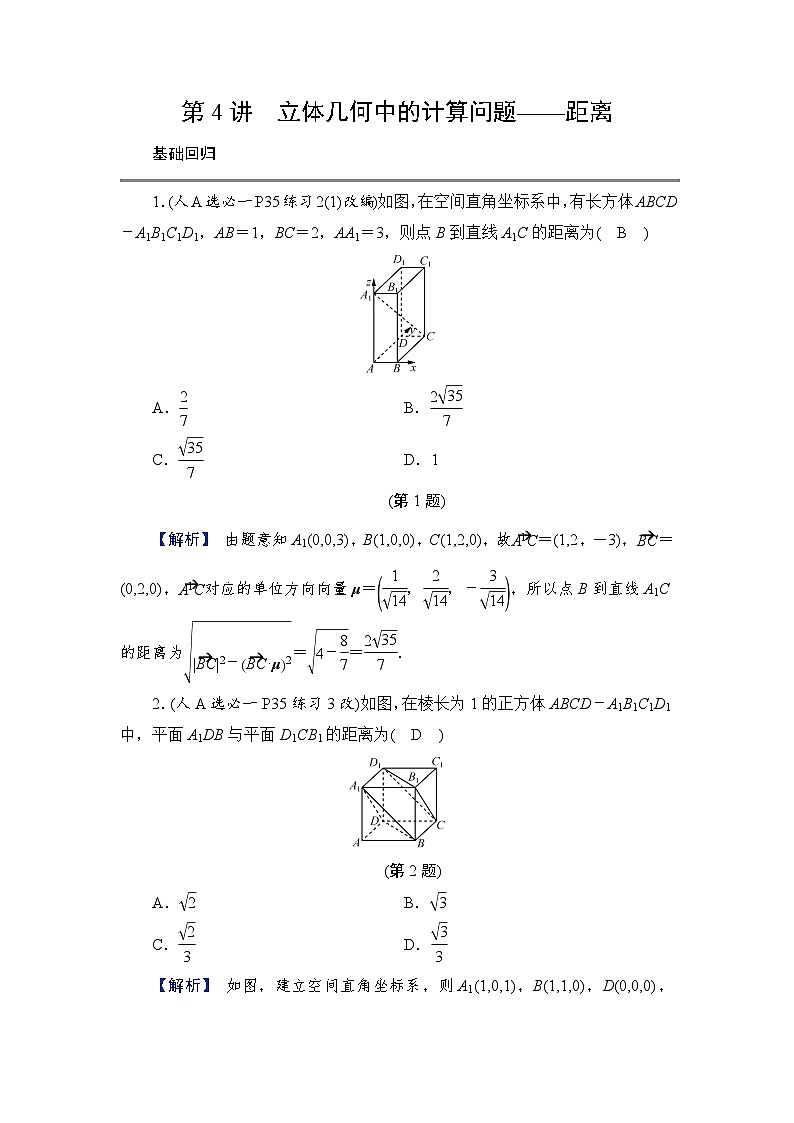
展开1.(人A选必一P35练习2(1)改编)如图,在空间直角坐标系中,有长方体ABCD-A1B1C1D1,AB=1,BC=2,AA1=3,则点B到直线A1C的距离为( B )
A.eq \f(2,7)B.eq \f(2\r(,35),7)
C.eq \f(\r(,35),7)D.1
(第1题)
【解析】 由题意知A1(0,0,3),B(1,0,0),C(1,2,0),故eq \(A1C,\s\up6(→))=(1,2,-3),eq \(BC,\s\up6(→))=(0,2,0),eq \(A1C,\s\up6(→))对应的单位方向向量μ=eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,\r(,14)),\f(2,\r(,14)),-\f(3,\r(,14)))),所以点B到直线A1C的距离为eq \r(,\(\s\up7(),\s\d5(|\(BC,\s\up6(→))|2-\(BC,\s\up6(→))·μ2)))=eq \r(,4-\f(8,7))=eq \f(2\r(,35),7).
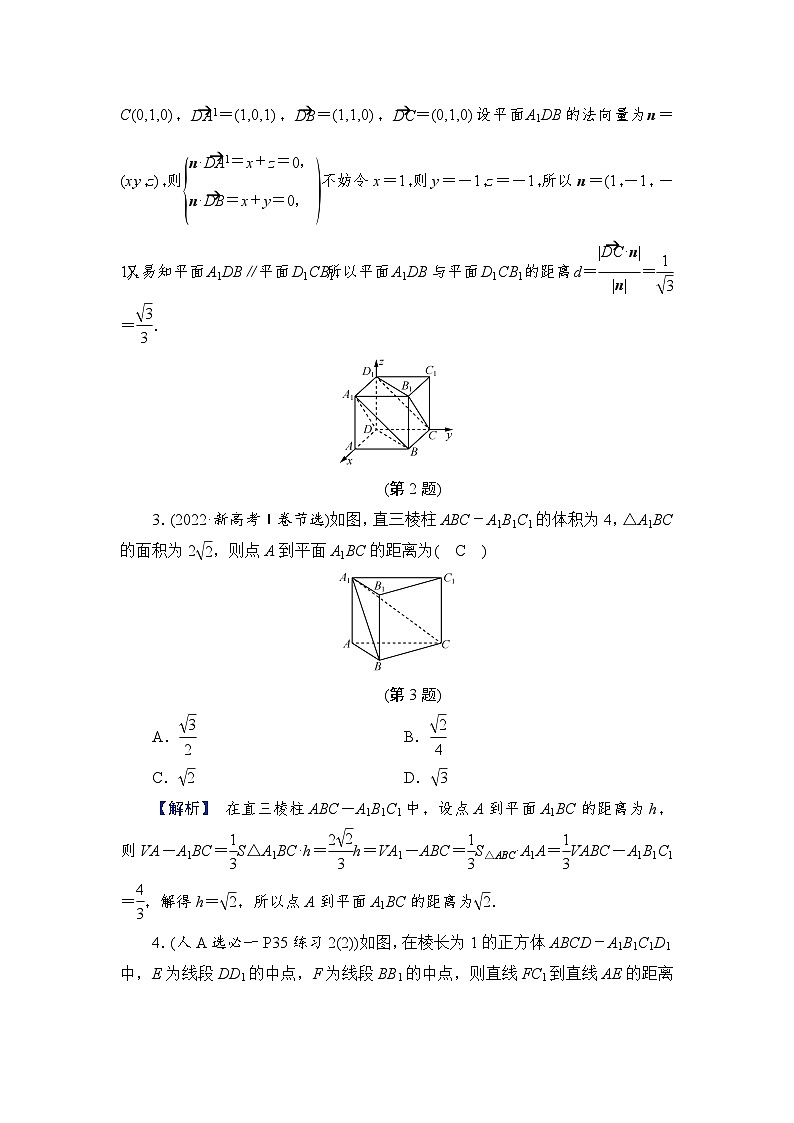
2.(人A选必一P35练习3改)如图,在棱长为1的正方体ABCD-A1B1C1D1中,平面A1DB与平面D1CB1的距离为( D )
(第2题)
A.eq \r(2)B.eq \r(3)
C.eq \f(\r(2),3)D.eq \f(\r(3),3)
【解析】 如图,建立空间直角坐标系,则A1(1,0,1),B(1,1,0),D(0,0,0),C(0,1,0),eq \(DA1,\s\up6(→))=(1,0,1),eq \(DB,\s\up6(→))=(1,1,0),eq \(DC,\s\up6(→))=(0,1,0).设平面A1DB的法向量为n=(x,y,z),则eq \b\lc\{(\a\vs4\al\c1(n·\(DA1,\s\up6(→))=x+z=0,,n·\(DB,\s\up6(→))=x+y=0,))不妨令x=1,则y=-1,z=-1,所以n=(1,-1,-1),又易知平面A1DB∥平面D1CB1,所以平面A1DB与平面D1CB1的距离d=eq \f(|\(DC,\s\up6(→))·n|,|n|)=eq \f(1,\r(3))=eq \f(\r(3),3).
(第2题)
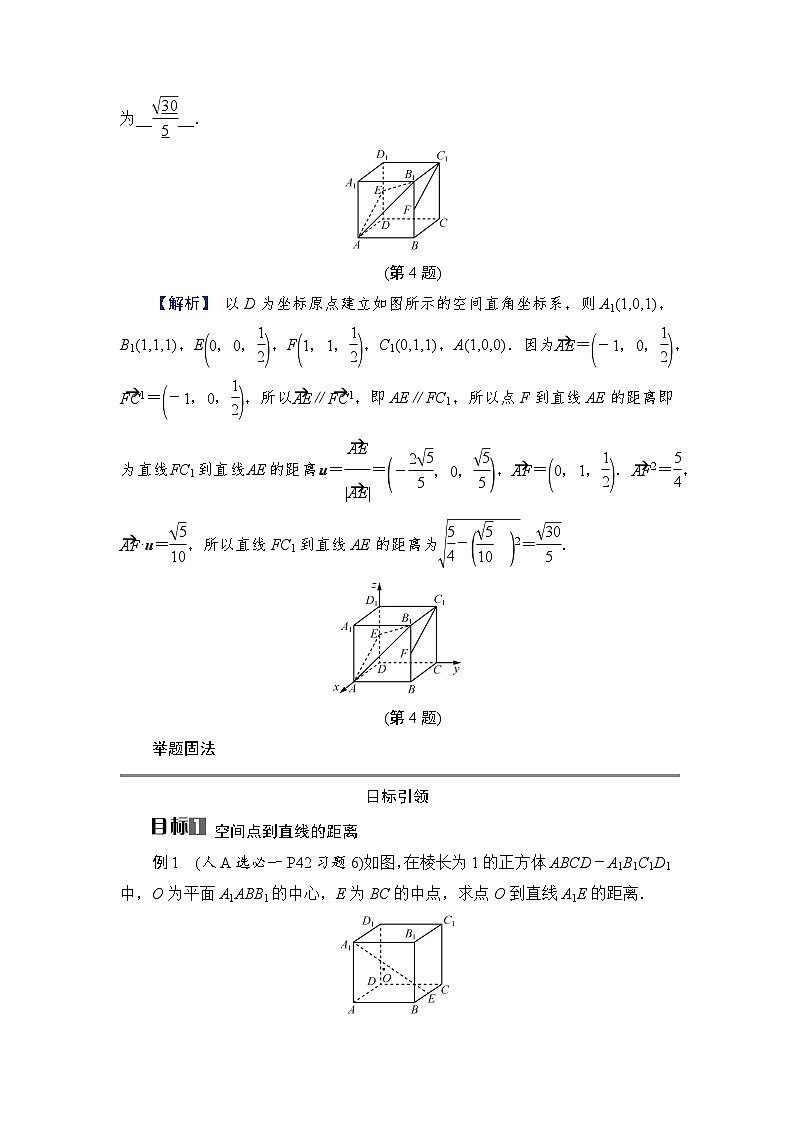
3.(2022·新高考Ⅰ卷节选)如图,直三棱柱ABC-A1B1C1的体积为4,△A1BC的面积为2eq \r(,2),则点A到平面A1BC的距离为( C )
(第3题)
A.eq \f(\r(,3),2)B.eq \f(\r(,2),4)
C.eq \r(,2)D.eq \r(,3)
【解析】 在直三棱柱ABC-A1B1C1中,设点A到平面A1BC的距离为h,则VA-A1BC=eq \f(1,3)S△A1BC·h=eq \f(2\r(,2),3)h=VA1-ABC=eq \f(1,3)S△ABC·A1A=eq \f(1,3)VABC-A1B1C1=eq \f(4,3),解得h=eq \r(,2),所以点A到平面A1BC的距离为eq \r(,2).
4.(人A选必一P35练习2(2))如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段DD1的中点,F为线段BB1的中点,则直线FC1到直线AE的距离为__eq \f(\r(30),5)__.
(第4题)
【解析】 以D为坐标原点建立如图所示的空间直角坐标系,则A1(1,0,1),B1(1,1,1),Eeq \b\lc\(\rc\)(\a\vs4\al\c1(0,0,\f(1,2))),Feq \b\lc\(\rc\)(\a\vs4\al\c1(1,1,\f(1,2))),C1(0,1,1),A(1,0,0).因为eq \(AE,\s\up6(→))=eq \b\lc\(\rc\)(\a\vs4\al\c1(-1,0,\f(1,2))),eq \(FC1,\s\up6(→))=eq \b\lc\(\rc\)(\a\vs4\al\c1(-1,0,\f(1,2))),所以eq \(AE,\s\up6(→))∥eq \(FC1,\s\up6(→)),即AE∥FC1,所以点F到直线AE的距离即为直线FC1到直线AE的距离.u=eq \f(\(AE,\s\up6(→)),|\(AE,\s\up6(→))|)=eq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(2\r(5),5),0,\f(\r(5),5))),eq \(AF,\s\up6(→))=eq \b\lc\(\rc\)(\a\vs4\al\c1(0,1,\f(1,2))).eq \(AF,\s\up6(→))2=eq \f(5,4),eq \(AF,\s\up6(→))·u=eq \f(\r(5),10),所以直线FC1到直线AE的距离为eq \r(\f(5,4)-\b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(5),10)))2)=eq \f(\r(30),5).
(第4题)
举题固法
目标引领
空间点到直线的距离
例1 (人A选必一P42习题6)如图,在棱长为1的正方体ABCD-A1B1C1D1中,O为平面A1ABB1的中心,E为BC的中点,求点O到直线A1E的距离.
(例1)
【解答】 方法一:建立如图所示的空间直角坐标系,则A1(1,0,1),Eeq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2),1,0)),Oeq \b\lc\(\rc\)(\a\vs4\al\c1(1,\f(1,2),\f(1,2))),eq \(OA1,\s\up6(→))=eq \b\lc\(\rc\)(\a\vs4\al\c1(0,-\f(1,2),\f(1,2))),eq \(A1E,\s\up6(→))=eq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(1,2),1,-1)),|eq \(OA1,\s\up6(→))|=eq \r(,\f(1,4)+\f(1,4))=eq \f(\r(,2),2),cs〈eq \(OA1,\s\up6(→)),eq \(A1E,\s\up6(→))〉=eq \f(\(OA1,\s\up6(→))·\(A1E,\s\up6(→)),|\(OA1,\s\up6(→))||\(A1E,\s\up6(→))|)=eq \f(-1,\f(\r(,2),2)×\f(3,2))=-eq \f(2\r(,2),3),所以点O到直线A1E的距离为|eq \(OA1,\s\up6(→))|×eq \r(,\(\s\up7(),\s\d5(1-cs2〈\(OA1,\s\up6(→)),\(A1E,\s\up6(→))〉)))=eq \f(\r(,2),2)×eq \r(,1-\b\lc\(\rc\)(\a\vs4\al\c1(-\f(2\r(,2),3)))2)=eq \f(\r(,2),2)×eq \f(1,3)=eq \f(\r(,2),6).
方法二:建立如图所示的空间直角坐标系,则A1(1,0,1),Eeq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2),1,0)),Oeq \b\lc\(\rc\)(\a\vs4\al\c1(1,\f(1,2),\f(1,2))).因为eq \(A1E,\s\up6(→))=eq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(1,2),1,-1)),u=eq \f(\(A1E,\s\up6(→)),|\(A1E,\s\up6(→))|)=eq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(1,3),\f(2,3),-\f(2,3))),eq \(OA1,\s\up6(→))=eq \b\lc\(\rc\)(\a\vs4\al\c1(0,-\f(1,2),\f(1,2))),所以eq \(OA1,\s\up6(→))·u=-eq \f(2,3),所以点O到直线A1E的距离为eq \r(,\(\s\up7(),\s\d5(\(OA1,\s\up6(→))2-\(OA1,\s\up6(→))·u2)))=eq \r(,\f(1,2)-\f(4,9))=eq \f(\r(,2),6).
(例1)
变式1 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为正方形,且PA=AB=2,F为棱PD的中点,点M在PA上,且PM=2MA,则CD的中点E到直线MF的距离是__eq \f(\r( ,65),5)__.
(变式1)
【解析】 因为PA⊥平面ABCD,底面ABCD为正方形,所以以点A为坐标原点,以AB,AD,AP所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系,则E(1,2,0),F(0,1,1),Meq \b\lc\(\rc\)(\a\vs4\al\c1(0,0,\f(2,3))),eq \(FM,\s\up6(→))=eq \b\lc\(\rc\)(\a\vs4\al\c1(0,-1,-\f(1,3))),eq \(FE,\s\up6(→))=(1,1,-1),cs∠MFE=eq \f(\(FM,\s\up6(→))·\(FE,\s\up6(→)),|\(FM,\s\up6(→))||\(FE,\s\up6(→))|)=eq \f(-\f(2,3),\f(\r(10),3)×\r(3))=-eq \f(\r(30),15),所以sin∠MFE=eq \r(1-cs2∠MFE)=eq \f(\r(195),15),所以CD的中点E到直线MF的距离d=|eq \(FE,\s\up6(→))|sin∠EFM=eq \r(3)×eq \f(\r(195),15)=eq \f(\r(65),5).
(变式1)
空间点到面的距离
例2 如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,求点O到平面ABC的距离.
(例2)
【解答】 方法一:如图(1),取BC的中点D,连接AD,OD.因为OA,OB,OC两两垂直,OB=OC,所以AB=AC,OD⊥BC,AD⊥BC.又OD∩AD=D,所以BC⊥平面OAD.过点O作OH⊥AD于点H,则OH⊥平面ABC,OH的长就是所要求的距离.由题知BC=2eq \r(,2),OD=eq \r(,OC2-CD2)=eq \r(,2).因为OA⊥OB,OA⊥OC,OB∩OC=O,所以OA⊥平面OBC,因为OD⊂平面OBC,所以OA⊥OD,所以AD=eq \r(,OA2+OD2)=eq \r(,3).在Rt△OAD中,OH=eq \f(OA·OD,AD)=eq \f(\r(,2),\r(,3))=eq \f(\r(,6),3).
(例2(1))
方法二:由题意知AB=AC=eq \r(,5),BC=2eq \r(,2),从而S△ABC=eq \f(1,2)×2eq \r(,2)×eq \r(,\r(,5)2-\r(,2)2)=eq \r(,6).由VO-ABC=eq \f(1,3)S△ABC·OH=eq \f(1,6)OA·OB·OC=eq \f(2,3),知OH=eq \f(\r(,6),3).
方法三:如图(2),建立空间直角坐标系,则O(0,0,0),A(0,0,1),B(2,0,0),C(0,2,0),所以eq \(AB,\s\up6(→))=(2,0,-1),eq \(OB,\s\up6(→))=(2,0,0),eq \(AC,\s\up6(→))=(0,2,-1).设平面ABC的法向量为n=(x,y,z),则由eq \b\lc\{(\a\vs4\al\c1(n·\(AB,\s\up6(→))=2x-z=0,,n·\(AC,\s\up6(→))=2y-z=0.))取x=1,则n=(1,1,2).故点O到平面ABC的距离d=eq \f(|\(OB,\s\up6(→))·n|,|n|)=eq \f(2,\r(,1+1+4))=eq \f(2,\r(,6))=eq \f(\r(,6),3).
(例2(2))
变式2-1 (2023·济南三月模拟)如图,在四棱锥P-ABCD中,△ABD是等边三角形,PA=PB=PD,BC=CD.
(变式2-1)
(1) 求证:BD⊥PC;
【解答】 如图,连接AC,交BD于点O,连接PO,由AD=AB,CD=BC,AC=AC,可得△ABC≌△ADC,所以∠BAC=∠DAC.又AO=AO,所以△AOB≌△AOD,所以BO=OD,即O为BD中点.在等腰三角形PBD中,BD⊥OP.在等腰三角形BCD中,BD⊥OC.因为OP∩OC=O,所以BD⊥平面POC.又PC⊂平面POC,所以BD⊥PC.
(2) 若BD=2eq \r(,3),CD=AP=eq \r(,7),求点A到平面PCD的距离.
【解答】 由(1)可得,AC⊥BD,又CD=eq \r(,7),OD=eq \f(1,2)BD=eq \r(,3),所以CO=eq \r(,CD2-OD2)=2,AO=eq \r(,3)OD=3.由于P-ABD为正三棱锥,故点P在底面ABD的垂足一定在AO上,设垂足为M,根据正三棱锥的性质可得AM=eq \f(2,3)AO=2,PM=eq \r(,AP2-AM2)=eq \r(,3).如图,以OA,OB所在直线分别为x轴,y轴建立空间直角坐标系,可得A(3,0,0),C(-2,0,0),D(0,-eq \r(,3),0),P(1,0,eq \r(,3)),eq \(PC,\s\up6(→))=(-3,0,-eq \r(,3)),eq \(DC,\s\up6(→))=(-2,eq \r(,3),0),eq \(AC,\s\up6(→))=(-5,0,0).设平面PCD的法向量为n=(x,y,z),则eq \b\lc\{(\a\vs4\al\c1(n·\(PC,\s\up6(→))=0,,n·\(DC,\s\up6(→))=0,))即eq \b\lc\{(\a\vs4\al\c1(-3x-\r(,3)z=0,,-2x+\r(,3)y=0,))不妨令x=eq \r(,3),可得n=(eq \r(,3),2,-3),所以点A到平面PCD的距离d=eq \f(|n·\(AC,\s\up6(→))|,|n|)=eq \f(5\r(,3),4),故点A到平面PCD的距离为eq \f(5\r(,3),4).
(变式2-1)
变式2-2 如图,在四面体ABCD中,AB=AD,BC=CD,E为BD的中点,F为AC上一点.
(变式2-2)
(1) 求证:平面ACE⊥平面BDF;
【解答】 在四面体ABCD中,AB=AD,BC=CD,E为BD的中点,则AE⊥BD,CE⊥BD,而AE∩CE=E,AE,CE⊂平面ACE,所以BD⊥平面ACE.又BD⊂平面BDF,所以平面ACE⊥平面BDF.
(2) 若∠BCD=90°,∠BAD=60°,AC=eq \r(,3)BC=2eq \r(,3),求点B到平面ACD的距离.
【解答】 依题意,BC=CD=2,∠BCD=90°,则BD=2eq \r(,2),CE=eq \r(,2).又∠BAD=60°,则AB=AD=BD=2eq \r(,2),AE=eq \r(,6).在△ACE中,cs∠AEC=eq \f(AE2+CE2-AC2,2AE·CE)=eq \f(6+2-12,2×\r(,6)×\r(,2))=-eq \f(\r(,3),3),则sin∠AEC=eq \f(\r(,6),3),S△AEC=eq \f(1,2)AE·CEsin∠AEC=eq \f(1,2)eq \r(,6)×eq \r(,2)×eq \f(\r(,6),3)=eq \r(,2).由(1)得BD⊥平面ACE,所以VB-ACD=eq \f(1,3)S△AEC·BD=eq \f(4,3).因为AD2+CD2=12=AC2,即∠ADC=90°,则S△ACD=eq \f(1,2)AD·CD=2eq \r(,2),令点B到平面ACD的距离为h,则VB-ACD=eq \f(1,3)S△ACD·h=eq \f(1,3)×2eq \r(,2)h=eq \f(4,3),解得h=eq \r(,2),所以点B到平面ACD的距离为eq \r(,2).
随堂内化
1.(2023·长沙模拟)若空间中有三点P(1,-2,-2),M(2,-3,1),N(3,-2,2),则点P到直线MN的距离为( A )
A.2eq \r(,2)B.2eq \r(,3)
C.3D.2eq \r(,5)
【解析】 因为eq \(MN,\s\up6(→))=(1,1,1),所以eq \(MN,\s\up6(→))的一个单位方向向量为u=eq \f(\r(,3),3)(1,1,1).因为eq \(PM,\s\up6(→))=(1,-1,3),故|eq \(PM,\s\up6(→))|=eq \r(,12+-12+32)=eq \r(,11),eq \(PM,\s\up6(→))·u=eq \f(\r(,3),3)(1-1+3)=eq \r(,3),所以点P到直线MN的距离为eq \r(,\(PM,\s\up6(→))2-\(PM,\s\up6(→))·u2)=eq \r(,11-3)=2eq \r(,2).
2.如图,在长方体ABCD-A1B1C1D1中,AB=2,BC=1,则直线AA1与平面BDD1B1的距离为( C )
(第2题)
A.eq \r(,5)B.eq \f(\r(,5),5)
C.eq \f(2\r(,5),5)D.2eq \r(,5)
【解析】 因为ABCD-A1B1C1D1为长方体,所以平面BDD1B1⊥平面ABCD,过A作AE⊥BD于点E,则AE⊥平面BDD1B1,所以直线AA1与平面BDD1B1的距离为AE.在Rt△ABD中,由等面积法可得AE=eq \f(AD×AB,BD)=eq \f(BC×AB,BD)=eq \f(1×2,\r(,12+22))=eq \f(2\r(,5),5).
3.如图,在几何体ABCDEF中,AD∥BC,∠BAD=eq \f(π,2),AB=AD=2BC=4,AE∥CF,AE=2CF=2,AE⊥平面ABCD,则点E到直线DF的距离为__eq \f(8\r(105),21)__.
(第3题)
【解析】 由题知AB,AD,AE两两垂直,所以以A为坐标原点,eq \(AB,\s\up6(→)),eq \(AD,\s\up6(→)),eq \(AE,\s\up6(→))的方向分别为x,y,z轴的正方向建立如图所示的空间直角坐标系,则B(4,0,0),D(0,4,0),E(0,0,2),F(4,2,1).eq \(DE,\s\up6(→))=(0,-4,2),eq \(DF,\s\up6(→))=(4,-2,1),eq \(BD,\s\up6(→))=(-4,4,0),eq \(BF,\s\up6(→))=(0,2,1),eq \(EF,\s\up6(→))=(4,2,-1).因为cs〈eq \(DE,\s\up6(→)),eq \(DF,\s\up6(→))〉=eq \f(10,2\r(5)×\r(21))=eq \f(\r(105),21),所以sin〈eq \(DE,\s\up6(→)),eq \(DF,\s\up6(→))〉=eq \f(4\r(21),21),所以点E到直线DF的距离为|eq \(DE,\s\up6(→))|sin〈eq \(DE,\s\up6(→)),eq \(DF,\s\up6(→))〉=2eq \r(5)×eq \f(4\r(21),21)=eq \f(8\r(105),21).
(第3题)
4.如图,在直三棱柱ABC-A1B1C1中,若∠ACB=90°,AC=BC=eq \f(1,2)AA1=1,D是棱AA1的中点,则点C到平面BDC1的距离为__eq \f(\r(,6),3)__.
(第4题)
【解析】 建立如图所示的空间直角坐标系,则A(1,0,0),C(0,0,0),B(0,1,0),D(1,0,1),C1(0,0,2).设平面BDC1的法向量为n=(x,y,z),eq \(BC,\s\up6(→))=(0,-1,0),eq \(BC1,\s\up6(→))=(0,-1,2),eq \(BD,\s\up6(→))=(1,-1,1),则eq \b\lc\{(\a\vs4\al\c1(n·\(BD,\s\up6(→))=x-y+z=0,,n·\(BC1,\s\up6(→))=-y+2z=0.))取z=1,得n=(1,2,1),从而点C到平面BDC1的距离为d=eq \f(|\(BC,\s\up6(→))·n|,|n|)=eq \f(\r(,6),3).
(第4题)
2024年高考数学重难点突破讲义:学案 第3讲 立体几何中的计算问题——二面角: 这是一份2024年高考数学重难点突破讲义:学案 第3讲 立体几何中的计算问题——二面角,共15页。
2024年高考数学重难点突破讲义:学案 第2讲 立体几何中的计算问题——线线角与线面角: 这是一份2024年高考数学重难点突破讲义:学案 第2讲 立体几何中的计算问题——线线角与线面角,共12页。
2024年高考数学重难点突破讲义:学案 第1讲 立体几何中的证明问题: 这是一份2024年高考数学重难点突破讲义:学案 第1讲 立体几何中的证明问题,共10页。试卷主要包含了下列结论正确的是等内容,欢迎下载使用。












