备考2024届高考数学一轮复习讲义第八章平面解析几何第6讲双曲线
展开(1)定义
在平面内到两定点F1,F2的距离的差的① 绝对值 等于常数(小于|F1F2|且大于零)的点的轨迹叫做双曲线.定点F1,F2叫做双曲线的② 焦点 ,两焦点间的距离叫做③ 焦距 .
集合语言:P={M|||MF1|-|MF2||=2a,2a<|F1F2|},|F1F2|=2c,其中a,c为常数且a>0,c>0.
a.当2a=2c时,P点的轨迹是④ 两条射线 ;
b.当2a>2c时,P点轨迹不存在.
(2)标准方程
a.中心在坐标原点,焦点在x轴上的双曲线的标准方程为⑤ x2a2-y2b2=1 (a>0,b>0);
b.中心在坐标原点,焦点在y轴上的双曲线的标准方程为⑥ y2a2-x2b2=1 (a>0,b>0).
规律总结
焦点位置的判断
在双曲线的标准方程中,看x2项与y2项的系数的正负,若x2项的系数为正,则焦点在x轴上;若y2项的系数为正,则焦点在y轴上,即“焦点位置看正负,焦点随着正的跑”.
思维拓展
双曲线的第二定义、第三定义
双曲线的第二定义:{P||PF|d=e,e>1,F∉l,其中F为定点,l为定直线,e为离心率,d为点P到直线l的距离}.
双曲线的第三定义:{P|kPA·kPB=e2-1,e>1,其中kPA,kPB分别表示点P与两定点A,B连线的斜率,e为离心率}(注意,此时确定的双曲线不包含两个顶点,且焦点在x轴上).
2.双曲线的几何性质
(1)双曲线的几何性质
(2)特殊双曲线
常用结论
1.双曲线的焦点三角形与焦半径
F1,F2分别为双曲线x2a2-y2b2=1(a>0,b>0)的左、右焦点,点P是双曲线上一点,则
(1)S△PF1F2=b2tanθ2,其中θ为∠F1PF2.
(2)△PF1F2内切圆圆心的横坐标的绝对值为定值a.
(3)当点P(x0,y0)在双曲线右支上时,|PF1|=ex0+a,|PF2|=ex0-a;当点Px0,y0在双曲线左支上时,|PF1|=-ex0-a,|PF2|=-ex0+a.
(4)当点P在双曲线右支上时,|PF1|min=a+c,|PF2|min=c-a.
2.双曲线中两个常见的直角三角形
如图所示,F1,F2分别为双曲线x2a2-y2b2=1(a>0,b>0)的左、右焦点,A为右顶点,过点F2向渐近线引垂线,垂足为C,过点A向x轴引垂线交渐近线于点B,则△COF2≌△AOB,且有|OC|=|OA|=a,|F2C|=|AB|=b,|OF2|=|OB|=c.
1.下列说法正确的是( D )
A.平面内到点F1(0,4),F2(0,-4)距离之差的绝对值等于8的点的轨迹是双曲线
B.关于x,y的方程x2m-y2n=1(mn>0)表示焦点在x轴上的双曲线
C.双曲线y29-x24=1的渐近线方程是y=±23x
D.等轴双曲线的渐近线互相垂直,离心率等于2
2.[浙江高考]渐近线方程为x±y=0的双曲线的离心率是( C )
A.22B.1C.2D.2
解析 因为双曲线的渐近线方程为x±y=0,所以无论双曲线的焦点在x轴上还是在y轴上,都满足a=b,所以c=2a,所以双曲线的离心率e=ca=2.故选C.
3.[2023北京高考]已知双曲线C的焦点为(-2,0)和(2,0),离心率为2,则C的标准方程为 x22-y22=1 .
解析 解法一 因为双曲线C的焦点为(-2,0)和(2,0),所以c=2,且焦点在x轴上.又离心率e=2,所以ca=2,所以a=2,则b2=c2-a2=2,所以双曲线C的标准方程为x22-y22=1.
解法二 因为双曲线C的离心率e=2,所以该双曲线为等轴双曲线,即a=b.又双曲线C的焦点为(-2,0)和(2,0),所以c=2,且焦点在x轴上,所以a2+b2=c2=4,所以a2=b2=2,所以双曲线C的标准方程为x22-y22=1.
4.已知等轴双曲线过点(5,3),则该双曲线方程为 x216-y216=1 .
解析 设双曲线方程为x2-y2=λ(λ≠0),将(5,3)代入方程,可得λ=52-32=16,所以双曲线方程为x2-y2=16,即x216-y216=1.
5.[教材改编]设双曲线x29-y2b2=1(b>0)的焦点为F1,F2,P为双曲线上的一点,若|PF1|=5,则|PF2|= 11 .
解析 由双曲线的方程x29-y2b2=1(b>0),可得a=3,根据双曲线的定义可知PF1-PF2=±2a=±6,又|PF1|=5,则|PF2|=11.
6.已知双曲线C:y2a2-x2b2=1(a>0,b>0)的焦距为43,实轴长为42,则双曲线C的渐近线方程为 2x±y=0 .
解析 由题意知,2c=43,2a=42,则b=c2-a2=2,所以C的渐近线方程为y=±abx=±2x,即2x±y=0.
研透高考 明确方向
命题点1 双曲线的定义及应用
例1 (1)[全国卷Ⅲ]设双曲线C:x2a2-y2b2=1(a>0,b>0)的左、右焦点分别为F1,F2,离心率为5.P是C上一点,且F1P⊥F2P.若△PF1F2的面积为4,则a=( A )
A.1B.2C.4D.8
解析 解法一 设|PF1|=m,|PF2|=n,P为双曲线右支上一点,则由双曲线的定义得m-n=2a.由题意得S△PF1F2=12mn=4,且m2+n2=4c2=(m-n)2+2mn=4a2+16,又e=ca=5,故c2a2=a2+4a2=5,所以a=1,故选A.
解法二 由题意及双曲线焦点三角形的结论,得S△PF1F2=b2tan45°=4,得b2=4,又c2a2=5,c2=b2+a2,所以a=1.
(2)已知圆C1:(x+3)2+y2=1,C2:(x-3)2+y2=9,动圆M同时与圆C1和圆C2相外切,则动圆圆心M的轨迹为( C )
A.双曲线B.椭圆
C.双曲线左支D.双曲线右支
解析 设动圆M的半径为r,由动圆M同时与圆C1和圆C2相外切,得|MC1|=1+r,|MC2|=3+r,|MC2|-|MC1|=2<6,所以动圆圆心M的轨迹是以点C1-3,0和C23,0为焦点的双曲线的左支.
方法技巧
1.双曲线定义的主要应用
(1)确认平面内与两定点有关的动点轨迹是否为双曲线;
(2)解决与焦点有关的距离或范围问题.
2.解决焦点三角形问题常利用双曲线的定义以及余弦定理.
训练1 (1)已知P是双曲线C:x22-y2=1右支上一点,直线l是双曲线C的一条渐近线.P在l上的射影为Q,F1是双曲线C的左焦点,则|PF1|+|PQ|的最小值为( D )
A.1B.2+155
C.4+155D.22+1
解析 设双曲线的右焦点为F2,因为|PF1|-|PF2|=22,所以|PF1|=22+|PF2|,|PF1|+|PQ|=22+|PF2|+|PQ|.当且仅当Q,P,F2三点共线,且P在Q,F2之间时,|PF2|+|PQ|最小,且最小值为点F2到直线l的距离.点F2到直线l的距离d=1,故|PQ|+|PF1|的最小值为22+1,故选D.
(2)已知F1,F2分别为双曲线C:x2-y2=2的左、右焦点,点P在C上,∠F1PF2=60°,则△F1PF2的面积为 23 .
解析 解法一 不妨设点P在双曲线的右支上,则|PF1|-|PF2|=2a=22,在△F1PF2中,由余弦定理,得cs∠F1PF2=|PF1|2+|PF2|2-|F1F2|22|PF1||PF2|=12,所以|PF1|·|PF2|=8,所以S△F1PF2=12|PF1|·|PF2|·sin 60°=23.
解法二 由题意可得双曲线C的标准方程为x22-y22=1,所以可得b2=2,由双曲线焦点三角形的面积公式S△PF1F2=b2tan∠F1PF22,可得S△F1PF2=2tan30°=23.
命题点2 求双曲线的标准方程
例2 (1)已知定点F1(-2,0),F2(2,0),N是圆O:x2+y2=1上任意一点,点F1关于点N的对称点为M,线段F1M的垂直平分线与直线F2M相交于点P,则点P的轨迹方程是( B )
A.x2+y23=1B.x2-y23=1
C.x23+y2=1D.x23-y2=1
解析 如图,当点P在y轴左侧时,连接ON,PF1.因为|ON|=12|F2M|=1,所以|F2M|=2,由PN所在直线为线段MF1的垂直平分线,可得|PF1|=|PM|=|PF2|-|F2M|=|PF2|-2,所以|PF2|-|PF1|=2<|F1F2|=4.同理,当点P在y轴右侧时,|PF1|-|PF2|=2<|F1F2|=4.故点P的轨迹是以F1,F2为焦点的双曲线,对应的方程为x2-y23=1.
(2)[2023天津高考]双曲线x2a2-y2b2=1(a>0,b>0)的左、右焦点分别为F1,F2.过F2作其中一条渐近线的垂线,垂足为P.已知|PF2|=2,直线PF1的斜率为24,则双曲线的方程为( D )
A.x28-y24=1B.x24-y28=1
C.x24-y22=1D.x22-y24=1
解析 解法一 由题意可知该渐近线方程为y=bax,直线PF2的方程为y=-ab(x-c),与y=bax联立并解得x=a2c,y=abc,即P(a2c,abc).因为直线PF2与渐近线y=bax垂直,所以PF2的长度即为点F2(c,0)到直线y=bax(即bx-ay=0)的距离,由点到直线的距离公式得|PF2|=bca2+b2=bcc=b,所以b=2.因为F1(-c,0),P(a2c,abc),且直线PF1的斜率为24,所以abca2c+c=24,化简得aba2+c2=24,又b=2,c2=a2+b2,所以2a2a2+4=24,整理得a2-22a+2=0,即(a-2)2=0,解得a=2.所以双曲线的方程为x22-y24=1,故选D.
解法二 因为过点F2向其中一条渐近线作垂线,垂足为P,且|PF2|=2,所以b=2,(双曲线中焦点到渐近线的距离为b)
再结合选项,排除选项B,C.若双曲线方程为x28-y24=1,则F1(-23,0),F2(23,0),渐近线方程为y=±22x,由题意可知该渐近线方程为y=22x,则直线PF2的方程为y=-2(x-23),与渐近线方程y=22x联立,得P(433,263),则kPF1=25,又直线PF1的斜率为24,所以双曲线方程x28-y24=1不符合题意,排除A.故选D.
方法技巧
求双曲线标准方程的两种方法
1.定义法
先根据双曲线定义确定a,b,c的值,再结合焦点的位置求出双曲线方程.
2.待定系数法
(1)先确定焦点在x轴上还是y轴上,设出标准方程,再由题中条件确定a2,b2的值;若不能确定焦点位置,可以设双曲线的方程为mx2+ny2=1(mn<0).
(2)常见设法
①与双曲线x2a2-y2b2=1(a>0,b>0)共渐近线的双曲线方程可设为x2a2-y2b2=λ(a>0,b>0,λ≠0);
②与双曲线x2a2-y2b2=1(a>0,b>0)共焦点的双曲线方程可设为x2a2-λ-y2b2+λ=1(-b2<λ
A.222B.4105C.7D.10
解析 由|PA|-|PB|=2<|AB|=4,知点P的轨迹是双曲线的右支,点P的轨迹方程为x2-y23=1(x≥1),又y=34-x2,所以x2=134,y2=274,所以|OP|=x2+y2=134+274=10,故选D.
(2)与双曲线x216-y24=1有相同的焦点,且经过点P(32,2)的双曲线的标准方程为 x212-y28=1 .
解析 解法一 设所求双曲线的左、右焦点分别为F1,F2,则F1(-25,0),F225,0,则|PF1|-|PF2|=(32+25)2+4-(32-25)2+4=212=2a,∴a=12,∴b2=c2-a2=8,故双曲线的标准方程为x212-y28=1.
解法二 设所求双曲线的方程为x216-λ-y24+λ=1(-4<λ<16).
∵双曲线过点P(32,2),∴1816-λ-44+λ=1,解得λ=4.
故双曲线的标准方程为x212-y28=1.
命题点3 双曲线的几何性质
角度1 渐近线
例3 (1)[2022北京高考]已知双曲线y2+x2m=1的渐近线方程为y=±33x,则m= -3 .
解析 依题意得m<0,令y2-x2-m=0,得y=±1-mx=±33x,解得m=-3.
(2)[2021新高考卷Ⅱ]已知双曲线C:x2a2-y2b2=1(a>0,b>0)的离心率e=2,则双曲线C的渐近线方程为 y=±3x .
解析 e=ca=1+(ba)2=2,得ba=3,所以双曲线C的渐近线方程为y=±bax=±3x.
方法技巧
(1)求双曲线x2a2-y2b2=1(a>0,b>0)的渐近线方程的方法:令x2a2-y2b2=0,即得两渐近线方程为xa±yb=0,也就是y=±bax.
(2)在双曲线x2a2-y2b2=1(a>0,b>0)中,离心率e与双曲线的渐近线的斜率k=±ba满足关系式k2=e2-1.
角度2 离心率
例4 (1)[2021全国卷甲]已知F1,F2是双曲线C的两个焦点,P为C上一点,且∠F1PF2=60°,|PF1|=3|PF2|,则C的离心率为( A )
A.72B.132C.7D.13
解析 设|PF2|=m,|PF1|=3m,则|F1F2|=m2+9m2-2×3m×m×cs60°=7m,所以C的离心率e=ca=2c2a=|F1F2||PF1|-|PF2|=7m2m=72.
(2)双曲线C:x2a2-y2b2=1(a>0,b>0)的左顶点为A,右焦点为F,过点A的直线交双曲线C于另一点B,当BF⊥AF时满足|AF|>2|BF|,则双曲线离心率e的取值范围是( B )
A.(1,2)B.(1,32)
C.(32,2)D.(1,3+32)
解析 由BF⊥AF,可得|BF|=b2a,又|AF|>2|BF|,|AF|=a+c,所以a+c>2·b2a,即a+c>2·c2-a2a,即a2+ac>2(c2-a2),两边同时除以a2,整理可得2e2-e-3<0,又e>1,则1<e<32.
所以双曲线离心率e的取值范围是(1,32).
(3)[2023新高考卷Ⅰ]已知双曲线C:x2a2-y2b2=1(a>0,b>0)的左、右焦点分别为F1,F2.点A在C上,点B在y轴上,F1A⊥F1B,F2A=-23F2B,则C的离心率为 355 .
解析 解法一 由题意可知,F1(-c,0),F2(c,0),设A(x1,y1),B(0,y0),所以F2A=(x1-c,y1),F2B=(-c,y0),因为F2A=-23F2B,所以x1-c=23c,y1=-23y0,即x1=53c,y1=-23y0,所以A(53c,-23y0).
F1A=(83c,-23y0),F1B=(c,y0),因为F1A⊥F1B,所以F1A·F1B=0,即83c2-23y02=0,解得y02=4c2.
因为点A(53c,-23y0)在双曲线C上,所以25c29a2-4y029b2=1,又y02=4c2,所以25c29a2-16c29b2=1,即25(a2+b2)9a2-16(a2+b2)9b2=1,化简得b2a2=45,所以e2=1+b2a2=95,所以e=355.
解法二 由前面解法一得A(53c,-23y0),y02=4c2,所以|AF1|=(53c+c)2+(-23y0)2=64c29+4y029=64c29+16c29=45c3,|AF2|=(53c-c)2+(-23y0)2=4c29+4y029=4c29+16c29=25c3,由双曲线的定义可得|AF1|-|AF2|=2a,即45c3-25c3=2a,即53c=a,所以双曲线的离心率e=ca=35=355.
方法技巧
1.求双曲线的离心率的方法
(1)直接利用公式求离心率:e=ca=1+(ba)2.
(2)利用双曲线的定义求离心率:在焦点三角形F1PF2中,设∠F1PF2=θ,∠PF1F2=α,∠PF2F1=β,则e=ca=|F1F2|||PF1|-|PF2||=sinθ|sinα-sinβ|.
(3)构造关于a,b,c的齐次式求离心率:由已知条件得出关于a,b,c的齐次式,然后转化为关于e的方程求解.
2.求双曲线离心率的取值范围的方法
(1)借助平面几何图形中的不等关系求解,如焦半径|PF1|∈[c-a,+∞)或|PF1|∈[a+c,+∞)、三角形中两边之和大于第三边等;
(2)考虑平面几何图形的临界位置,建立关于a,c的不等关系求解.
角度3 与双曲线性质有关的最值(范围)问题
例5 (1)[全国卷Ⅱ]设O为坐标原点,直线x=a与双曲线C:x2a2-y2b2=1(a>0,b>0)的两条渐近线分别交于D,E两点.若△ODE的面积为8,则C的焦距的最小值为( B )
A.4B.8C.16D.32
解析 由题意知双曲线的渐近线方程为y=±bax.因为D,E分别为直线x=a与双曲线C的两条渐近线的交点,所以不妨设D(a,b),E(a,-b),所以S△ODE=12×a×|DE|=12×a×2b=ab=8,所以c2=a2+b2≥2ab=16,当且仅当a=b=22时等号成立.所以c≥4,2c≥8,所以C的焦距的最小值为8,故选B.
(2)已知双曲线C:x2a2-y2b2=1(a>0,b>0)的两个顶点分别为A1,A2,F为双曲线的一个焦点,B为虚轴的一个端点,若在线段BF上(不含端点)存在两点P1,P2,使得∠A1P1A2=∠A1P2A2=π2,则双曲线的渐近线的斜率k的平方的取值范围是( A )
A.(1,5+12)B.(1,3+12)
C.(0,5+12)D.(3+12,32)
解析 不妨设点F为双曲线的左焦点,点B在y轴正半轴上,则F-c,0,B0,b,直线BF的方程为bx-cy=-bc.如图所示,以O为圆心,A1A2为直径作圆O,则P1,P2在圆O上.
由题意可知b>a,bcb2+c2<a,即b>a,baa2+b2<a2+2b2,解得1<b2a2<5+12,即双曲线的渐近线的斜率k的平方的取值范围是(1,5+12).
方法技巧
求解与双曲线性质有关的最值(范围)问题的方法
1.几何法:如果题中给出的条件有明显的几何特征,那么可以考虑用图形的性质来求解,特别是用双曲线的定义和平面几何的有关结论来求解.
2.代数法:构造函数或不等式,利用函数或不等式的性质求解.
训练3 (1)[2023绵阳二诊]设双曲线C:x2a2-y2b2=1(a>0,b>0)的右焦点为F,A,B两点在双曲线C上且关于原点对称,若|AB|=2|OF|(O为坐标原点),|BF|=3|AF|,则该双曲线的渐近线方程为( A )
A.6x±2y=0B.2x±6y=0
C.2x±3y=0D.3x±2y=0
解析 记F'为双曲线C的左焦点,连接AF',BF',则F,F'关于原点对称,又A,B也关于原点对称,所以四边形AFBF'为平行四边形,又|AB|=2|OF|,所以四边形AFBF'为矩形.因为|BF|=3|AF|,所以|AF'|=3|AF|,所以|AF'|-|AF|=2|AF|=2a,所以|AF|=a,|AF'|=3a.在Rt△FAF'中,AF2+AF'2=FF'2,所以a2+(3a)2=(2c)2,所以c2=5a22,又a2+b2=c2,所以b2=3a22,所以ba=62,所以双曲线C:x2a2-y2b2=1(a>0,b>0)的渐近线方程为y=±62x,即6x±2y=0,故选A.
(2)如图,设双曲线C:x2-y224=1的左、右焦点分别是F1、F2,点A是C右支上的一点,则|AF1|+4|AF2|的最小值为( C )
A.5B.6C.7D.8
解析 由双曲线C:x2-y224=1可得a2=1,b2=24,所以c2=a2+b2=25,所以a=1,c=5.由双曲线的定义可得|AF1|-|AF2|=2a=2,所以|AF1|=|AF2|+2,所以|AF1|+4|AF2|=|AF2|+4|AF2|+2.由双曲线的性质可知|AF2|≥c-a=4,令|AF2|=t,则t≥4,所以|AF1|+4|AF2|=t+4t+2.令f(t)=t+4t+2(t≥4),则ft在[4,+∞)上单调递增,(易忽视|AF2|的范围,错误地使用基本不等式求最值)
所以当t=4时,f(t)取得最小值4+44+2=7,此时点A为双曲线的右顶点(1,0),即|AF1|+4|AF2|的最小值为7.故选C.
(3)[2023湖北省重点中学联考]若双曲线x2a2-y2b2=1(a>0,b>0)的右支上存在两点A,B,使△ABM为正三角形(其中M为双曲线的右顶点),则离心率e的取值范围为 (1,233) .
解析 由题意,双曲线的渐近线方程为y=±bax.要使该双曲线右支上存在两点A,B,使△ABM为正三角形,则需过右顶点M,且斜率为33的直线与双曲线的右支有两个不同的交点,即只需斜率大于渐近线y=bax的斜率,所以33>ba,即b<33a,即b2<13a2,所以c2<a2+13a2,即c<233a.又e>1,所以1<e<233.课标要求
命题点
五年考情
命题分析预测
1.了解双曲线的定义、几何图形和标准方程,以及简单几何性质.
2.体会数形结合的思想.
双曲线的定义及应用
2020全国卷ⅢT11
该讲每年必考,命题热点为双曲线的定义、标准方程、渐近线、离心率,题型既有选择题、填空题,也有解答题,难度中等偏上.在2025年高考备考中,训练常规题型的同时,应强化有关解答题的训练.
求双曲线的标准方程
2023新高考卷ⅡT21;2023天津T9;2022新高考卷ⅡT21
双曲线的几何性质
2023新高考卷ⅠT16;2022全国卷乙T11;2022全国卷甲T14;2022北京T12;2021新高考卷ⅠT21;2021新高考卷ⅡT13;2021全国卷甲T5;2021全国卷乙T13;2020新高考卷ⅠT9;2020全国卷ⅠT15;2020全国卷ⅡT8;2020全国卷ⅢT11;2019全国卷ⅠT16 ;2019全国卷ⅡT11;2019全国卷ⅢT10
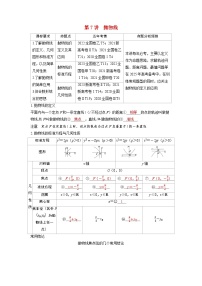
标准方程
x2a2-y2b2=1(a>0,b>0)
y2a2-x2b2=1(a>0,b>0)
图形
标准方程
x2a2-y2b2=1(a>0,b>0)
y2a2-x2b2=1(a>0,b>0)
几
何
性
质
范围
|x|≥a,y∈R
|y|≥a,x∈R
对称性
对称轴:⑦ x轴,y轴 ;对称中心:⑧ 原点
焦点
F1⑨ (-c,0) ,F2⑩ (c,0)
F1⑪ (0,-c) ,F2⑫ (0,c)
顶点
A1(-a,0),A2(a,0)
A1(0,-a),A2(0,a)
轴
线段A1A2,B1B2分别是双曲线的实轴和虚轴;实轴长为⑬ 2a ,虚轴长为⑭ 2b ;实半轴长为a,虚半轴长为b
焦距
|F1F2|=⑮ 2c
离心率
e=⑯ ca =1+b2a2,e∈⑰ (1,+∞)
渐近线
直线⑱ y=±bax
直线⑲ y=±abx
a,b,c
的关系
a2=⑳ c2-b2
等轴双曲线
共轭双曲线
定义
实轴长与虚轴长相等的双曲线叫做等轴双曲线.
如果一双曲线的实轴和虚轴分别是另一双曲线的虚轴和实轴,那么这两个双曲线互为共轭双曲线.
性质
(1)a=b;(2)e=2;(3)渐近线互相垂直;(4)等轴双曲线上任意一点到中心的距离是它到两焦点距离的等比中项.
(1)它们有共同的渐近线;(2)它们的四个焦点共圆;(3)它们的离心率的倒数的平方和等于1.
备考2024届高考数学一轮复习讲义第八章平面解析几何第5讲椭圆: 这是一份备考2024届高考数学一轮复习讲义第八章平面解析几何第5讲椭圆,共11页。
备考2024届高考数学一轮复习讲义第八章平面解析几何第3讲圆的方程: 这是一份备考2024届高考数学一轮复习讲义第八章平面解析几何第3讲圆的方程,共9页。
备考2024届高考数学一轮复习讲义第八章平面解析几何第1讲直线的方程: 这是一份备考2024届高考数学一轮复习讲义第八章平面解析几何第1讲直线的方程,共7页。