

备考2024届高考数学一轮复习讲义第二章函数第5讲对数与对数函数
展开(1)对数的概念
一般地,如果ax=N(a>0,且a≠1),那么数x叫做以a为底N的对数,记作① x=lgaN ,其中a叫做对数的② 底数 ,N叫做③ 真数 .
以10为底的对数叫做常用对数,记作④ lgN ;以e为底的对数叫做自然对数,记作⑤ lnN .
(2)对数的性质、运算性质及换底公式
2.对数函数的图象和性质
规律总结
1.对数函数y=lgax(a>0,且a≠1)的图象过定点(1,0),且过点(a,1),(1a,
-1),函数图象只在第一、四象限.
2.如图,作直线y=1,则该直线与四个函数图象交点的横坐标为相应的底数,故0<c<d<1<a<b.由此我们可得到以下规律:在第一象限内从左到右对数函数的底数逐渐增大.
注意 当对数函数的底数a的大小不确定时,需分a>1和0<a<1两种情况进行讨论.
3.反函数
指数函数y=ax(a>0,且a≠1)与对数函数y=lgax(a>0,且a≠1)互为反函数,它们的图象关于直线⑳ y=x 对称(如图所示).反函数的定义域、值域分别是原函数的值域、定义域,互为反函数的两个函数具有相同的单调性、奇偶性.
1.[全国卷Ⅰ]设alg34=2,则4-a=( B )
A.116B.19C.18D.16
解析 解法一 因为alg34=2,所以lg34a=2,则有4a=32=9,所以4-a=14a=19,故选B.
解法二 因为alg34=2,所以a=2lg34=lg39lg34=lg49,所以4a=9,所以4-a=14a=19,故选B.
2.[多选]以下说法正确的是( CD )
A.若MN>0,则lga(MN)=lgaM+lgaN
B.对数函数y=lgax(a>0且a≠1)在(0,+∞)上是增函数
C.函数y=ln 1+x1-x与y=ln(1+x)-ln(1-x)的定义域相同
D.对数函数y=lgax(a>0且a≠1)的图象过定点(1,0)且过点(a,1),(1a,
-1),函数图象只在第一、四象限
3.lg 25+lg 2·lg 50+(lg 2)2= 2 .
4.若lga34<1(a>0,且a≠1),则实数a的取值范围是 (0,34)∪(1,+∞) .
5.设lga2=m,lga3=n,则a2m+n的值为 12 .
6.[2023北京高考]已知函数f(x)=4x+lg2x,则f(12)= 1 .
解析 因为f(x)=4x+lg2x,所以f(12)=412+lg212=2+lg22-1=2-1=1.
研透高考 明确方向
命题点1 对数的运算
例1 (1)[2022天津高考]化简(2lg43+lg83)(lg32+lg92)的值为( B )
A.1B.2C.4D.6
解析 (2lg43+lg83)(lg32+lg92)=(2lg223+lg233)×(lg32+lg322)=(lg23+13lg23)(lg32+12lg32)=43×lg23×32×lg32=2,故选B.
(2)[2022浙江高考]已知2a=5,lg83=b,则4a-3b=( C )
A.25B.5C.259D.53
解析 由2a=5得a=lg25.又b=lg83=lg23lg28=13lg23,所以a-3b=lg25-lg23=lg253=lg453lg42=2lg453=lg4259,所以4a-3b=4lg4259=259,故选C.
方法技巧
对数运算的一般思路
(1)转化:①利用ab=N⇔b=lgaN(a>0且a≠1)对题目条件进行转化;②利用换底公式化为同底数的对数运算.
(2)利用恒等式:lga1=0,lgaa=1,lgaaN=N,algaM=M.
(3)拆分:将真数化为积、商或底数的指数幂形式,正用对数的运算性质化简.
(4)合并:将对数式化为同底数对数的和、差、倍数的运算,然后逆用对数的运算性质,转化为同底数对数的真数的积、商、幂的运算.
训练1 (1)[2024江苏省如皋市教学质量调研]我们知道,任何一个正实数N可以表示成N=a×10n(1≤a<10,n∈Z),此时lg N=n+lg a(0≤lg a<1).当n>0时,N是n+1位数,则41 000是( C )位数.(lg 2≈0.301 0)
A.601B.602C.603D.604
解析 由lg41 000=lg22 000=2 000lg 2≈2 000×0.301 0=602=602+lg 1,得n=602,所以41 000是603位数.故选C.
(2)[2024山东泰安第二中学模拟](2+1027)-23+2lg32-lg349-5lg259= -716 .
解析 原式=[(43)3]-23+lg34-lg349-5lg53=(43)-2+lg39-3 =916+2-3=-716.
命题点2 对数函数的图象及应用
例2 (1)[浙江高考]在同一直角坐标系中,函数y=1ax,y=lga(x+12)(a>0,且a≠1)的图象可能是( D )
AB
CD
解析 若0<a<1,则函数y=1ax是增函数,y=lga(x+12)是减函数且其图象过点(12,0),结合选项可知,选项D可能成立;若a>1,则y=1ax是减函数,而y=lga(x+12)是增函数且其图象过点(12,0),结合选项可知,没有符合的图象.故选D.
(2)已知当0<x≤14时,有x<lgax,则实数a的取值范围为 (116,1) .
解析 若x<lgax在x∈(0,14]时成立,则0<a<1,且y=x的图象在y=lgax图象的下方,作出y=x,y=lgax的图象如图所示.由图象知14<lga14,所以0
与对数函数有关的图象问题的求解策略
1.对于图象的识别,一般通过观察图象的变化趋势、利用已知函数的性质、函数图象上的特殊点(与坐标轴的交点、最高点、最低点等)排除不符合要求的选项.
2.对于对数型函数的图象,一般从最基本的对数函数的图象入手,通过平移、伸缩、对称变换而得到.
训练2 (1)[多选/2024辽宁省部分学校模拟]已知ax=b-x(a>0且a≠1,b>0且b≠1),则函数y=lga(-x)与y=bx的图象可能是( AB )
解析 因为ax=b-x,即ax=(1b)x,所以a=1b,当a>1时,0<b<1,函数y=bx在R上单调递减,且过点(0,1),因为y=lgax与y=lga(-x)的图象关于y轴对称,故y=lga(-x)在(-∞,0)上单调递减且过点(-1,0),故A符合题意.
当0<a<1时,b>1,函数y=bx在R上单调递增,且过点(0,1),y=lga(-x)在(-∞,0)上单调递增且过点(-1,0),故B符合题意.故选AB.
(2)[2024安徽省皖江名校联考]已知函数f(x)=|lg3|x||,x≠0,0,x=0,设a,b,c,d是四个互不相同的实数,且满足f(a)=f(b)=f(c)=f(d),则|a|+|b|+|c|+|d|的取值范围是 (4,+∞) .
解析 作出函数f(x)的图象,如图所示,易知f(x)图象关于y轴对称.
设f(a)=f(b)=f(c)=f(d)=m(m>0),且a>b>c>d,作直线y=m,则由图象得0<b<1<a,则由题意知,lg3a=
-lg3b,且a=-d,b=-c,所以ab=1,即b=1a,则|a|+|b|+|c|+|d|=
2(a+b)=2(a+1a)>4,所以|a|+|b|+|c|+|d|的取值范围是(4,+∞).
命题点3 对数函数的性质及应用
角度1 比较大小
例3 (1)[2021新高考卷Ⅱ]若a=lg52,b=lg83,c=12,则( C )
A.c<b<aB.b<a<cC.a<c<bD.a<b<c
解析 a=lg52=lg54<lg55=12=c,b=lg83=lg89>lg88=12=c,所以a<c<b.故选C.
(2)[2024天津市蓟州区第一中学模拟]已知函数f(x)在R上是增函数,若a=
f(lg215),b=f(lg24.1),c=f(20.5),则a,b,c的大小关系为( A )
A.a<c<bB.b<a<c
C.c<b<aD.c<a<b
解析 lg215=-lg25<-lg24=-2,lg24.1>lg24=2,20.5=2∈(1,2),故lg215<20.5<lg24.1.由于f(x)在R上是增函数,故f(lg215)<f(20.5)<f(lg24.1),所以a<c<b.故选A.
方法技巧
比较对数值大小的常用方法
1.底数相同时,比较真数的大小;真数相同时,利用换底公式转化为底数相同的形式,再比较大小,也可以借助对数函数的图象比较大小.
2.当底数和真数都不相同时,常借助0,1或题干中出现的有理数等中间量比较大小,也可以通过作差或者作商比较大小.
角度2 解对数方程或不等式
例4 (1)[2024湘豫名校联考]已知函数f(x)=lg2|x|+x2,则不等式f(ln x)+
f(-ln x)<2的解集为( D )
A.(1e,1)B.(1e,e)
C.(1,e)D.(1e,1)∪(1,e)
解析 由题可知函数f(x)的定义域为(-∞,0)∪(0,+∞),∴ln x≠0.
∵f(-x)=lg2|-x|+(-x)2=lg2|x|+x2=f(x),
∴f(x)是偶函数,∴由f(ln x)+f(-ln x)<2可得2f(ln x)<2,即f(ln x)<1.
当x>0时,f(x)=lg2x+x2.
∵y=lg2x和y=x2在(0,+∞)上都是单调递增的,∴f(x)在(0,+∞)上单调递增,又f(1)=1,∴|ln x|<1且ln x≠0,∴1e<x<e且x≠1,所以原不等式的解集为(1e,1)∪(1,e).故选D.
(2)[2024江苏省淮安市五校联考]已知x=4lg6x-9lg6x,y=9lg4y+6lg4y,则xy的值为( B )
A.5+12B. 5-12
C.5+1D.5-1
解析 令lg6x=m,lg4y=n,则x=6m,y=4n.
由x=4lg6x-9lg6x,y=9lg4y+6lg4y可得6m=4m-9m,4n=9n+6n,
进而可得(32)m=1-(32)2m,故(32)m+(32)2m=1,同理得(32)2n+(32)n=1,所以(32)m与(32)n均为方程t2+t-1=0的实数根,
由t2+t-1=0,解得t=-1+52或t=-1-52,
因为(32)m>0,(32)n>0,
所以(32)m=(32)n=-1+52.
由于函数y=(32)x为增函数,所以m=n,xy=6m4n=(32)m=-1+52,故选B.
方法技巧
1.(1)lgaf(x)=b⇔f(x)=ab(a>0,且a≠1).
(2)lgaf(x)=lgag(x)⇔f(x)=g(x)(f(x)>0,g(x)>0).
2.解简单对数不等式,先统一底数,化为形如lgaf(x)>lgag(x)的不等式,再借助y=lgax的单调性求解.
角度3 对数函数性质的应用
例5 (1)[全国卷Ⅱ]设函数f(x)=ln|2x+1|-ln|2x-1|,则f(x)( D )
A.是偶函数,且在(12,+∞)单调递增
B.是奇函数,且在(-12,12)单调递减
C.是偶函数,且在(-∞,-12)单调递增
D.是奇函数,且在(-∞,-12)单调递减
解析 由2x+1≠0,2x-1≠0,得函数f(x)的定义域为(-∞,-12)∪(-12,12)∪(12,
+∞),其关于原点对称,因为f(-x)=ln|2(-x)+1|-ln|2(-x)-1|=ln|2x-1|-ln|2x+1|=-f(x),所以函数f(x)为奇函数,排除A,C.当x∈
(-12,12)时,f(x)=ln(2x+1)-ln(1-2x),易知函数f(x)单调递增,排除B.当x∈(-∞,-12)时,f(x)=ln(-2x-1)-ln(1-2x)=ln2x+12x-1=ln(1+22x-1),易知函数f(x)单调递减,故选D.
(2)[全国卷Ⅰ]若2a+lg2a=4b+2lg4b,则( B )
A.a>2bB.a<2b
C.a>b2D.a<b2
解析 令f(x)=2x+lg2x,因为y=2x在(0,+∞)上单调递增,y=lg2x在(0,
+∞)上单调递增,所以f(x)=2x+lg2x在(0,+∞)上单调递增.又2a+lg2a=4b+2lg4b=22b+lg2b<22b+lg2(2b),所以f(a)<f(2b),所以a<2b.故选B.
方法技巧
对数型复合函数的单调性问题的求解策略
(1)对于y=lgaf(x)型的复合函数的单调性,有以下结论:函数y=lgaf(x)的单调性与函数u=f(x)(f(x)>0)的单调性在a>1时相同,在0<a<1时相反.
(2)研究y=f(lgax)型的复合函数的单调性,一般用换元法,即令t=lgax,则只需研究t=lgax及y=f(t)的单调性即可.
注意 研究对数型复合函数的单调性,一定要坚持“定义域优先”原则,否则所得范围易出错.
训练3 (1)[2024河南名校联考]“a≤2”是“函数f(x)=ln(x2-ax+12)在区间(2,+∞)上单调递增”的( A )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
解析 二次函数y=x2-ax+12图象的对称轴为x=a2,若函数f(x)=ln(x2-ax+12)在区间(2,+∞)上单调递增,则根据复合函数的单调性可得a2≤2,4-2a+12≥0,即a≤94,故“a≤2”是“函数f(x)=ln(x2-ax+12)在区间(2,+∞)上单调递增”的充分不必要条件.故选A.
(2)[2024河南商丘高三名校联考]已知a=lg64,b=lg53,c=lg76,则( B )
A.a<b<cB.b<a<c
C.b<c<aD.c<a<b
解析 由题意得a,b,c∈(0,1),
∵lg64·lg67<(lg64+lg672)2=(lg6282)2<1,
∴lg64<1lg67=lg76,即a<c.
∵a=lg64=lg64256>lg64216=34,b=lg53=lg5481<lg54125=34,∴a>b.综上所述,可得b<a<c.故选B.
(3)[2024湖北名校联考改编]已知奇函数f(x)=lg1+kx1+x(k≠1),则不等式-1<f(x)<lg12的解集为 (13,911) .
解析 因为f(x)为奇函数,所以f(-x)+f(x)=lg1-kx1-x+lg1+kx1+x=lg1-k2x21-x2=0,所以k2=1.因为k≠1,所以k=-1,则由-1<f(x)<lg12,得lg110<lg1-x1+x<lg12,所以110<1-x1+x<12,解得13<x<911.课标要求
命题点
五年考情
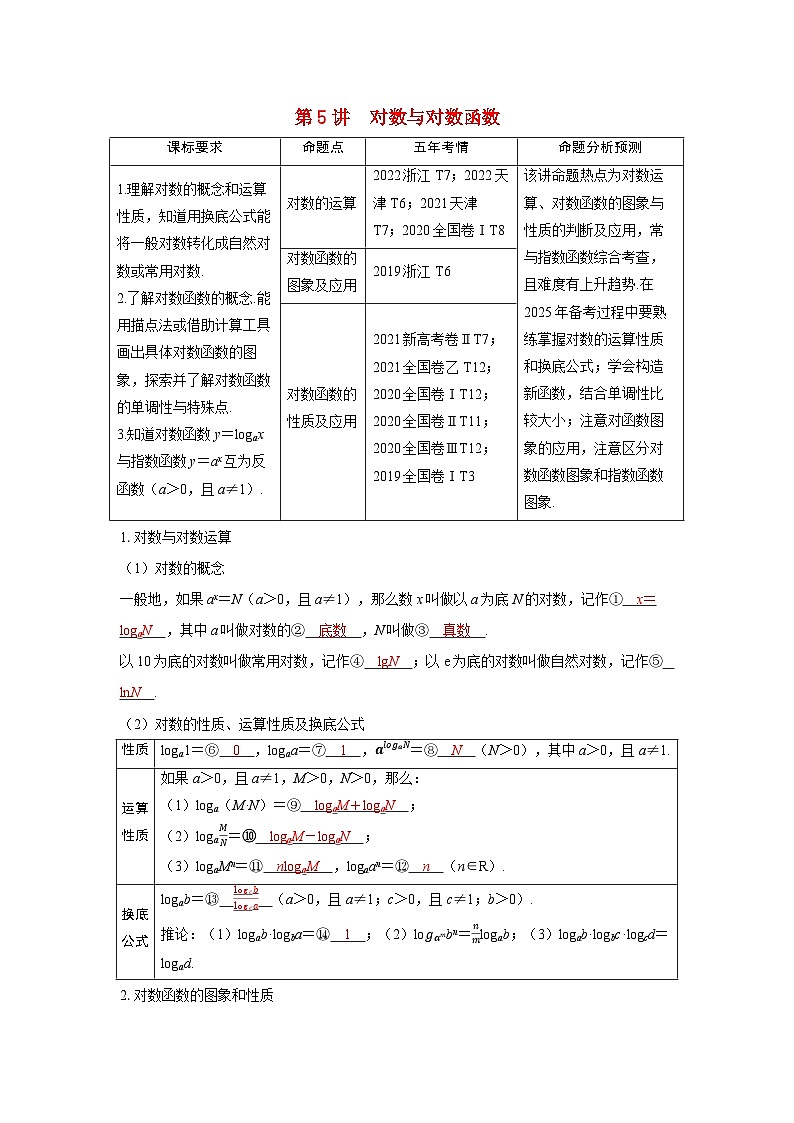
命题分析预测
1.理解对数的概念和运算性质,知道用换底公式能将一般对数转化成自然对数或常用对数.
2.了解对数函数的概念.能用描点法或借助计算工具画出具体对数函数的图象,探索并了解对数函数的单调性与特殊点.
3.知道对数函数y=lgax与指数函数y=ax互为反函数(a>0,且a≠1).
对数的运算
2022浙江T7;2022天津T6;2021天津T7;2020全国卷ⅠT8
该讲命题热点为对数运算、对数函数的图象与性质的判断及应用,常与指数函数综合考查,且难度有上升趋势.在2025年备考过程中要熟练掌握对数的运算性质和换底公式;学会构造新函数,结合单调性比较大小;注意对函数图象的应用,注意区分对数函数图象和指数函数图象.
对数函数的图象及应用
2019浙江T6
对数函数的性质及应用
2021新高考卷ⅡT7;2021全国卷乙T12;2020全国卷ⅠT12;2020全国卷ⅡT11;2020全国卷ⅢT12;2019全国卷ⅠT3
性质
lga1=⑥ 0 ,lgaa=⑦ 1 ,algaN=⑧ N (N>0),其中a>0,且a≠1.
运算
性质
如果a>0,且a≠1,M>0,N>0,那么:
(1)lga(M·N)=⑨ lgaM+lgaN ;
(2)lgaMN=⑩ lgaM-lgaN ;
(3)lgaMn=⑪ nlgaM ,lgaan=⑫ n (n∈R).
换底
公式
lgab=⑬ lgcblgca (a>0,且a≠1;c>0,且c≠1;b>0).
推论:(1)lgab·lgba=⑭ 1 ;(2)lgambn=nmlgab;(3)lgab·lgbc·lgcd=lgad.
函数
y=lgax(a>1)
y=lgax(0<a<1)
图象
性质
定义域:⑮ (0,+∞) .
值域:⑯ R .
图象过定点⑰ (1,0) ,即恒有lga1=0.
当x>1时,y>0;当0<x<1时,y<0.
当x>1时,y<0;当0<x<1时,y>0.
在(0,+∞)上单调递⑱ 增 .
在(0,+∞)上单调递⑲ 减 .
备考2024届高考数学一轮复习讲义第二章函数第1讲函数的概念及其表示: 这是一份备考2024届高考数学一轮复习讲义第二章函数第1讲函数的概念及其表示,共7页。
备考2024届高考数学一轮复习讲义第二章函数第8讲函数模型的应用: 这是一份备考2024届高考数学一轮复习讲义第二章函数第8讲函数模型的应用,共6页。
备考2024届高考数学一轮复习讲义第二章函数第4讲幂函数指数与指数函数: 这是一份备考2024届高考数学一轮复习讲义第二章函数第4讲幂函数指数与指数函数,共10页。













