专题11 反比例函数综合过关检测-备战2024年中考数学一轮复习考点全预测（全国通用）

这是一份专题11 反比例函数综合过关检测-备战2024年中考数学一轮复习考点全预测（全国通用），文件包含专题11反比例函数综合过关检测-备战2024年中考数学一轮复习考点帮全国通用解析版docx、专题11反比例函数综合过关检测-备战2024年中考数学一轮复习考点帮全国通用考试版docx等2份试卷配套教学资源，其中试卷共21页， 欢迎下载使用。

选择题（本题共10小题，每小题3分，共30分）。
1．若点A（1，3）是反比例函数y＝（k≠0）图象上一点，则常数k的值为（ ）
A．3B．﹣3C．D．
【答案】A
【解答】解：∵点A（1，3）在反比例函数y＝（k≠0）图象上，
∴k＝1×3＝3，
故选：A．
2．下列各点中，在反比例函数y＝图象上的是（ ）
A．（3，1）B．（﹣3，1）C．（3，）D．（，3）
【答案】A
【解答】解：A、∵3×1＝3，∴此点在反比例函数的图象上，故A正确；
B、∵（﹣3）×1＝﹣3≠3，∴此点不在反比例函数的图象上，故B错误；
C、∵3×＝1≠3，∴此点不在反比例函数的图象上，故C错误；
D、∵×3＝1≠3，∴此点不在反比例函数的图象上，故D错误．
故选：A．
3．如果点A（﹣1，y1）、B（1，y2）、C（2，y3）是反比例函数图象上的三个点，则下列结论正确的是（ ）
A．y1＞y3＞y2B．y3＞y2＞y1C．y2＞y1＞y3D．y3＞y1＞y2
【答案】A
【解答】解：∵反比例函数的比例系数为﹣1，
∴图象的两个分支在二、四象限；
∵第四象限的点的纵坐标总小于在第二象限的纵坐标，点A在第二象限，点B、C在第四象限，
∴y1最大，
∵1＜2，y随x的增大而增大，
∴y2＜y3，
∴y1＞y3＞y2．
故选：A．
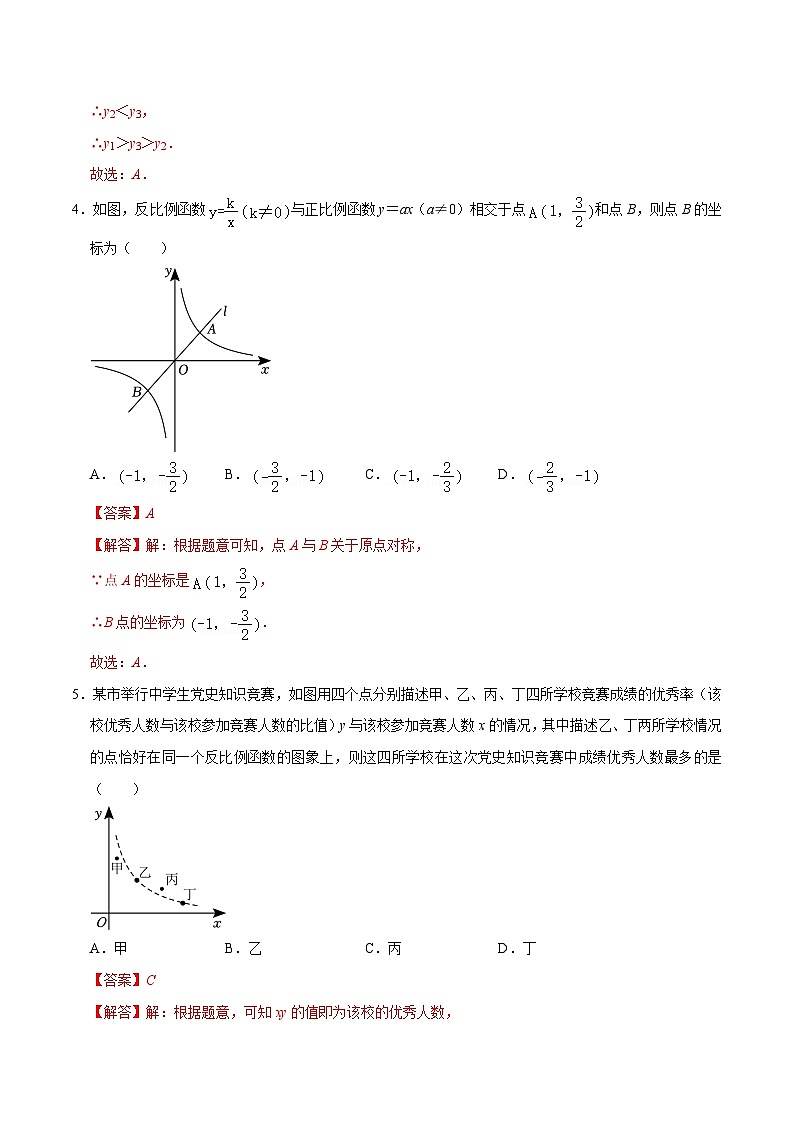
4．如图，反比例函数与正比例函数y＝ax（a≠0）相交于点和点B，则点B的坐标为（ ）
A．B．C．D．
【答案】A
【解答】解：根据题意可知，点A与B关于原点对称，
∵点A的坐标是，
∴B点的坐标为．
故选：A．
5．某市举行中学生党史知识竞赛，如图用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率（该校优秀人数与该校参加竞赛人数的比值）y与该校参加竞赛人数x的情况，其中描述乙、丁两所学校情况的点恰好在同一个反比例函数的图象上，则这四所学校在这次党史知识竞赛中成绩优秀人数最多的是（ ）
A．甲B．乙C．丙D．丁
【答案】C
【解答】解：根据题意，可知xy的值即为该校的优秀人数，
∵描述乙、丁两学校情况的点恰好在同一个反比例函数的图象上，
∴乙、丁两学校的优秀人数相同，
∵点丙在反比例函数图象上面，点甲在反比例函数图象下面，
∴丙学校的xy的值最大，即优秀人数最多，甲学校的xy的值最小，即优秀人数最少，
故选：C．
6．已知反比例函数，下列说法不正确的是（ ）
A．图象经过点（﹣3，2）
B．图象分别位于第二、四象限内
C．在每个象限内y的值随x的值增大而增大
D．x≥﹣1时，y≥6
【答案】D
【解答】解：因为（﹣3）×2＝﹣6，
所以A正确，不符合题意；
因为反比例函数，
所以图象分别位于第二、四象限内；在每个象限内y的值随x的值增大而增大；
所以B、C正确，不符合题意；
当x≥﹣1时，y≥6或y＜0，
所以D错误，符合题意，
故选：D．
7．反比例函数y＝中，当x＞0时，y随x的增大而增大，则m的取值范围是（ ）
A．m＞B．m＜2C．m＜D．m＞2
【答案】A
【解答】解：∵反比例函数y＝，当x＞0时y随x的增大而增大，
∴1﹣2m＜0，
∴m＞．
故选：A．
8．如图，正比例函数y1＝k1x的图象与反比例函数y2＝的图象相交于A、B两点，其中A点的横坐标为3，当y1＜y2时，x的取值范围是（ ）
A．x＜﹣3或x＞3B．x＜﹣3或0＜x＜3
C．﹣3＜x＜0或0＜x＜3D．﹣3＜x＜0或x＞3
【答案】B
【解答】解：∵正比例函数与反比例函数的图象均关于原点对称，点A的横坐标为3，
∴点B的横坐标为﹣3．
观察函数图象，发现：
当0＜x＜3或x＜﹣3时，正比例函数图象在反比例函数图象的下方，
∴当y1＜y2时，x的取值范围是x＜﹣3或0＜x＜3．
故选：B．
9．在同一平面直角坐标系中，函数y＝ax+b与（其中a，b是常数，ab≠0）的大致图象是（ ）
A．B．
C．D．
【答案】A
【解答】解：若a＞0，b＞0，
则y＝ax+b经过一、二、三象限，反比例函数y＝（ab≠0）位于一、三象限，
若a＞0，b＜0，
则y＝ax+b经过一、三、四象限，反比例函数数y＝（ab≠0）位于二、四象限，
若a＜0，b＞0，
则y＝ax+b经过一、二、四象限，反比例函数y＝（ab≠0）位于二、四象限，
若a＜0，b＜0，
则y＝ax+b经过二、三、四象限，反比例函数y＝（ab≠0）位于一、三象限，
故选：A．
10．如图，是反比例函数y＝和y＝（k1＜k2）在第一象限的图象，直线AB∥x轴，并分别交两条曲线于A、B两点，若S△AOB＝2，则k2﹣k1的值是（ ）
A．1B．2C．4D．8
【答案】C
【解答】解：设A（a，b），B（c，d），
代入得：k1＝ab，k2＝cd，
∵S△AOB＝2，
∴cd﹣ab＝2，
∴cd﹣ab＝4，
∴k2﹣k1＝4，
故选：C．
填空题(本题共6题，每小题2分，共12分）。
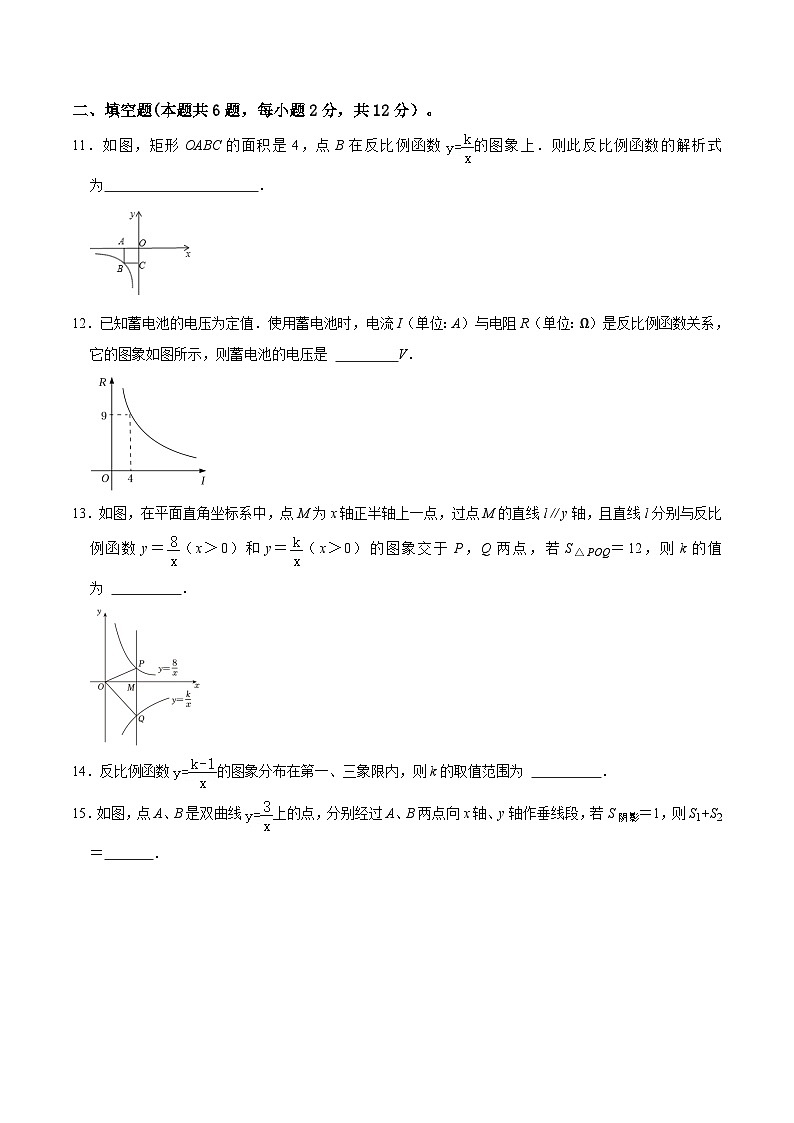
11．如图，矩形OABC的面积是4，点B在反比例函数的图象上．则此反比例函数的解析式为 y＝ ．
【答案】见试题解答内容
【解答】解：设BC＝a，AB＝b，则B点坐标为（﹣a，﹣b），AB•BC＝ab＝4，
将点B（﹣a，﹣b）代入y＝中，得k＝xy＝（﹣a）×（﹣b）＝ab＝4，
∴y＝．
故答案为：y＝．
12．已知蓄电池的电压为定值．使用蓄电池时，电流I（单位：A）与电阻R（单位：Ω）是反比例函数关系，它的图象如图所示，则蓄电池的电压是 36 V．
【答案】36．
【解答】解：设用电阻R表示电流I的函数解析式为，
∵过（4，9），
∴U＝4×9＝36，
故答案为：36．
13．如图，在平面直角坐标系中，点M为x轴正半轴上一点，过点M的直线l∥y轴，且直线l分别与反比例函数y＝（x＞0）和y＝（x＞0）的图象交于P，Q两点，若S△POQ＝12，则k的值为 ﹣16 ．
【答案】见试题解答内容
【解答】解：∵S△POQ＝S△OMQ+S△OMP，
∴|k|+×|8|＝12，
∴|k|＝16，
而k＜0，
∴k＝﹣16．
故答案为：﹣16．
14．反比例函数的图象分布在第一、三象限内，则k的取值范围为 k＞1 ．
【答案】k＞1．
【解答】解：由题意得，k﹣1＞0，
∴k＞1．
故答案为：k＞1．
15．如图，点A、B是双曲线上的点，分别经过A、B两点向x轴、y轴作垂线段，若S阴影＝1，则S1+S2＝ 4 ．
【答案】见试题解答内容
【解答】解：由题意可得，S1+S2＝2|k|﹣2S阴影＝2×3﹣2×1＝4，
故答案为：4．
16．为了做好校园疫情防控工作，校医每天早上对全校办公室和教室进行药物熏蒸消毒．消毒药物在一间教室内空气中的浓度y（单位：mg/m3）与时间x（单位：min）的函数关系如图所示：校医进行药物熏蒸时y与x的函数关系式为y＝2x，药物熏蒸完成后y与x成反比例函数关系，两个函数图象的交点为A（m，n）．教室空气中的药物浓度不低于2mg/m3时，对杀灭病毒有效．当m＝3时，本次消毒过程中有效杀灭病毒的时间为 8 min．
【答案】8．
【解答】解：当m＝3是，y＝2×3＝6，
∴A（3，6），
设熏蒸完后函数的关系式为：y＝，
∴k＝3×6＝18，
∴熏蒸完后函数的关系式为：y＝，
∵药物浓度不低于2mg/m3，
∴当2x≥2时，x≥1，
当y＝≥2时，x≤9，
∴有效时长为9﹣1＝8（min），
故答案为：8．
三、解答题（本题共7题，共58分）。
17．（8分）已知反比例函数的图象经过第一、三象限．
（1）求k的取值范围；
（2）若a＞0，此函数的图象过第一象限的两点（a+5，y1）（2a+1，y2），且y1＜y2，求a的取值范围．
【答案】（1）k＞4；
（2）0＜a＜4．
【解答】解：（1）∵反比例函数的图象经过第一、三象限，
∴k﹣4＞0，
解得：k＞4．
∴k的取值范围是：k＞4．
（2）∵反比例函数图象过第一象限的两点（a+5，y1）（2a+1，y2），且y1＜y2，
∴a+5＞2a+1，
解得：a＜4，
又∵a＞0，
∴a的取值范围是：0＜a＜4．
18．（6分）王芳同学在一次做电学实验时，记录下电流I（A）与电阻R（Ω）的一些对应值，通过描写连线，画出了I关于R的函数图象如图，求I与R之间的函数关系式，并求当电阻为4Ω时，电流的值是多少．
【答案】，当电阻为4Ω时，电流的值6A．
【解答】解：设，
∵当电阻R＝8Ω时，电流I＝3A，
∴U＝IR＝3×8＝24，
∴，
当电阻R＝4Ω时，电流，
∴当电阻为4Ω时，电流的值6A．
19．（8分）已知一次函数y＝kx+b（k≠0）与反比例函数（m≠0）的图象交于A（2，3），B（﹣6，n）两点．
（1）求一次函数和反比例函数的解析式；
（2）求△AOB的面积．
【答案】（1）反比例函数关系式为，一次函数关系式为；
（2）8．
【解答】解：（1）∵反比例函数（m≠0）的图象过点A（2，3），
∴m＝2×3＝6，
∴反比例函数关系式为y＝，
当x＝﹣6时，y＝＝﹣1，
∴点B（﹣6，﹣1）．
又∵一次函数y＝kx+b（k≠0）的图象过点A（2，3），B（﹣6，﹣1）．
∴，
解得，
∴一次函数的关系式为：y＝x+2，
∴反比例函数关系式为，一次函数关系式为；
（2）如图，直线AB与y轴的交点C（0，2），即OC＝2，
∴S△AOB＝S△BOC+S△AOC
＝×2×6+×2×2
＝6+2
＝8，
即：△AOB的面积为8．
20．（8分）如图，在平面直角坐标系xOy中，A（4，0），C（0，2）．点D是矩形OABC对角线的交点．已知反比例函数y＝（k≠0）在第一象限的图象经过点D，交BC于点M，交AB于点N．
（1）求点D的坐标和k的值；（2）反比例函数图象在点M到点N之间的部分（包含M，N两点）记为图形G，求图形G上点的横坐标x的取值范围．
【答案】（1）k＝2；
（2）1≤x≤4．
【解答】解：（1）∵点D是矩形OABC的对角线交点，
∴点D是矩形OABC的对角线AC的中点，
又∵A（4，0），C（0，2），
∴点D的坐标为（2，1）．
∵反比例函数的图象经过点D，
∴，
解得：k＝2．
（2）由题意可得：点M的纵坐标为2，点N的横坐标为4．
∵点M在反比例函数的图象上，
∴点M的坐标为（1，2），
∴1≤x≤4．
21．（8分）为防止病菌滋生，某校定期对教室进行喷雾消毒，某次消毒作业时，喷雾阶段教室内每立方米空气中含药量y（mg）是时间x（min）的正比例函数，喷雾完成后y是x的反比例函数（如图）．
（1）当x＞5时，求y关于x的函数解析式；
（2）已知每立方米空气中含药量不低于4mg时，消毒效果最好，求本次消毒每立方米空气中含药量不低于4mg的时长．
【答案】（1）当x＞5时，y关于x的函数解析式为y＝；
（2）本次消毒每立方米空气中含药量不低于4mg的时长为7.5min．
【解答】解：（1）当x＞5时，设y关于x的函数解析式为y＝，
把（5，8）代入解析式得：8＝，
解得k＝40，
∴当x＞5时，y关于x的函数解析式为y＝；
（2）根据题意得，当0＜x≤5时，y关于x的函数解析式为y＝x，
把y＝4代入y＝x得：x＝；
把y＝4代入y＝得：x＝10．
∵10﹣＝＝7.5（min），
∴本次消毒每立方米空气中含药量不低于4mg的时长为7.5min．
22．（10分）如图，取一根长1米的质地均匀木杆，用细绳绑在木杆的中点O处并将其吊起来，在中点的左侧距离中点30cm处挂一个重9.8牛的物体，在中点O右侧用一个弹簧秤向下拉，使木杆保持平衡，改变弹簧秤与中点O的距离L（单位：cm），看弹簧秤的示数F（单位：牛，精确到0.1牛）有什么变化．小慧在做此《数学活动》时，得到下表的数据：
结果老师发现其中有一个数据明显有错误．
（1）你认为当L＝ 10 cm时所对应的F数据是明显错误的；
（2）在已学过的函数中选择合适的模型求出F与L的函数关系式；
（3）若弹簧秤的最大量程是60牛，求L的取值范围．
【答案】（1）10；
（2）；
（3）L的取值范围是4.9cm≤L≤50cm．
【解答】解：（1）根据杠杆原理知 F•L＝30×9.8．
当L＝10cm时，F＝29.4牛顿．所以表格中数据错了；
（2）根据杠杆原理知F•L＝30×9.8．
∴F与L的函数关系式为：；
（3）当F＝60牛时，由得L＝4.9，
根据反比例函数的图象与性质可得L≥4.9，
∵由题意可知L≤50，
∴L的取值范围是4.9cm≤L≤50cm．
23．（10分）如图，在平面直角坐标系xOy中，一次函数y＝﹣x+5的图象与反比例函数y＝（k＞0）的图象相交于A，B两点，与x轴相交于点C，连接OB，且△BOC的面积为．
（1）求反比例函数的表达式；
（2）将直线AB向下平移，若平移后的直线与反比例函数的图象只有一个交点，试说明直线AB向下平移了几个单位长度？
【答案】见试题解答内容
【解答】解：（1）一次函数y＝﹣x+5中，令y＝0，解得x＝5，
∴C（5，0），
∴OC＝5，
作BD⊥OC于D，
∵△BOC的面积为，
∴OC•BD＝，即BD＝，
∴BD＝1，
∴点B的纵坐标为1，
代入y＝﹣x+5中，求得x＝4，
∴B（4，1），
∵反比例函数y＝（k＞0）的图象经过B点，
∴k＝4×1＝4，
∴反比例函数的解析式为y＝；
（2）将直线AB向下平移m（m＞0）个单位长度得直线解析式为y＝﹣x+5﹣m，
∵直线AB向下平移m（m＞0）个单位长度后与反比例函数的图象只有一个公共交点，
∴＝﹣x+5﹣m，
整理得x2+（m﹣5）x+4＝0，
Δ＝（m﹣5）2﹣4×1×4＝0，解得m＝9或m＝1，
即m的值为1或9L/cm
5
10
15
20
25
30
35
40
F/牛
58.8
60.2
19.6
14.7
11.8
9.8
8.4
7.4