专题10 一次函数综合过关检测-备战2024年中考数学一轮复习考点全预测（全国通用）

这是一份专题10 一次函数综合过关检测-备战2024年中考数学一轮复习考点全预测（全国通用），文件包含专题10一次函数综合过关检测-备战2024年中考数学一轮复习考点帮全国通用解析版docx、专题10一次函数综合过关检测-备战2024年中考数学一轮复习考点帮全国通用考试版docx等2份试卷配套教学资源，其中试卷共19页， 欢迎下载使用。

选择题（本题共10小题，每小题3分，共30分）。
1．（2023秋•铜陵期中）下列函数①y＝πx，②y＝﹣2x+3，③，④，⑤y＝x2﹣1中，是一次函数的有（ ）
A．1个B．2个C．3个D．4个
【答案】C
【解答】解：①y＝πx，是一次函数，符合题意；
②y＝﹣2x+3，是一次函数，符合题意；
③，x的次数不为1，不是一次函数，不符合题意；
④，是一次函数，符合题意；
⑤y＝x2﹣1x的次数不为1，不是一次函数，不符合题意；
即一次函数有①②④，共3个，
故选：C．
2．（2023•长沙模拟）已知一次函数y＝ax﹣4的函数值y随x的增大而减小，则该函数的图象大致是（ ）
A．B．
C．D．
【答案】B
【解答】解：∵一次函数y＝ax﹣4的函数值y随x的增大而减小，
∴a＜0，
∵b＝﹣4＜0，
∴y＝ax﹣4经过第二、三、四象限，
故选：B．
3．（2022秋•大东区校级期末）将一次函数y＝﹣2x的图象沿y轴向下平移4个单位长度后，所得图象的函数表达式为（ ）
A．y＝﹣2（x﹣4）B．y＝﹣2x+4C．y＝﹣2（x+4）D．y＝﹣2x﹣4
【答案】D
【解答】解：由上加下减”的原则可知，将一次函数y＝﹣2x的图象沿y轴向下平移4个单位长度后，所得图象的函数表达式为：y＝﹣2x﹣4．
故选：D．
4．（2022秋•碑林区期末）一次函数y＝kx+b图象经过（1，1），（2，﹣4），则k与b的值为（ ）
A．B．C．D．
【答案】C
【解答】解：把（1，1），（2，﹣4）代入一次函数y＝kx+b，
得，
解得：．
故选：C．
5．（2023春•乾安县期末）已知A（﹣，y1）、B（﹣，y2）、C（1，y3）是一次函数y＝﹣3x+b的图象上三点，则y1，y2，y3的大小关系是（ ）
A．y1＜y2＜y3B．y2＜y1＜y3C．y3＜y1＜y2D．y3＜y2＜y1
【答案】C
【解答】解：∵A（﹣，y1）、B（﹣，y2）、C（1，y3）是一次函数y＝﹣3x+b的图象上三点，
∴y1＝1+b，y2＝+b，y3＝﹣3+b．
∵﹣3+b＜1+b＜+b，
∴y3＜y1＜y2．
故选：C．
6．（2023•灞桥区校级二模）若一次函数y＝（m﹣1）x+m﹣2的图象不经过第二象限，则m的取值范围是（ ）
A．m＞1B．m＜2C．1＜m＜2D．1＜m≤2
【答案】D
【解答】解：∵一次函数y＝（m﹣1）x+m﹣2的图象不经过第二象限，
∴m﹣1＞0且m﹣2≤0，
解得1＜m≤2，
故选：D．
7．（2023春•开福区校级期末）对于函数y＝﹣2x+4，说法正确的是（ ）
A．点A（1，3）在这个函数图象上
B．y随着x的增大而增大
C．它的图象必过一、三象限
D．当x＞2时，y＜0
【答案】D
【解答】解：A．当x＝1时，y＝﹣2×1+4＝2，2≠3，
∴点（1，3）不在这个函数图象上，选项A不符合题意；
B．∵k＝﹣2＜0，
∴y随x的增大而减小，选项B不符合题意；
C．∵k＝﹣2＜0，b＝4＞0，
∴一次函数y＝﹣2x+4的图象经过第一、二、四象限，选项C不符合题意；
D．当x＞2时，y＜﹣2×2+4＝0，选项D符合题意．
故选：D．
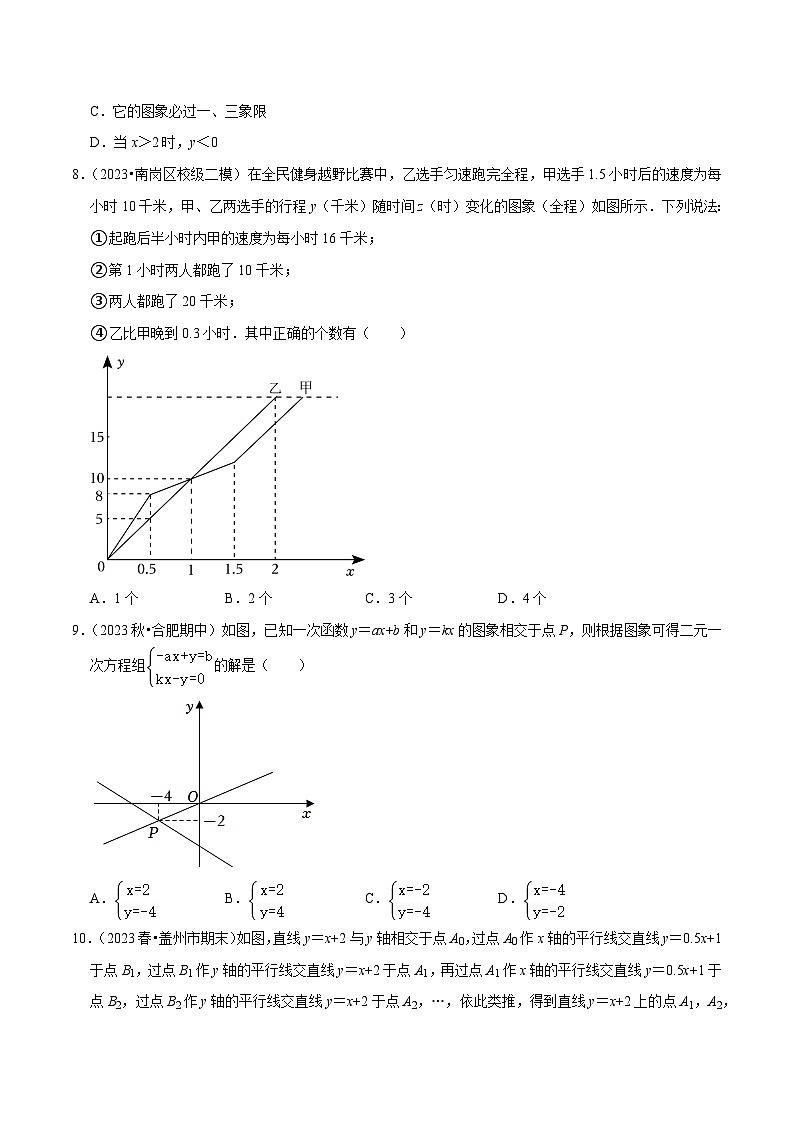
8．（2023•南岗区校级二模）在全民健身越野比赛中，乙选手匀速跑完全程，甲选手1.5小时后的速度为每小时10千米，甲、乙两选手的行程y（千米）随时间z（时）变化的图象（全程）如图所示．下列说法：
①起跑后半小时内甲的速度为每小时16千米；
②第1小时两人都跑了10千米；
③两人都跑了20千米；
④乙比甲晚到0.3小时．其中正确的个数有（ ）
A．1个B．2个C．3个D．4个
【答案】C
【解答】解：①起跑后半小时内甲的速度为8÷0.5＝16千米/小时，故①正确；
②根据函数图象的交点坐标，可得第1小时两人都跑了10千米，故②正确；
③根据甲1小时跑10km，可得2小时跑20km，故两人都跑了20千米，故③正确；
④根据0.5～1.5小时内，甲半小时跑2km，可得1小时跑4km，故1.5小时跑了12km，剩余的8km需要的时间为8÷10＝0.8小时，根据1.5+0.8﹣2＝0.3，可得甲比乙晚到0.3小时，故④错误．
故选：C．
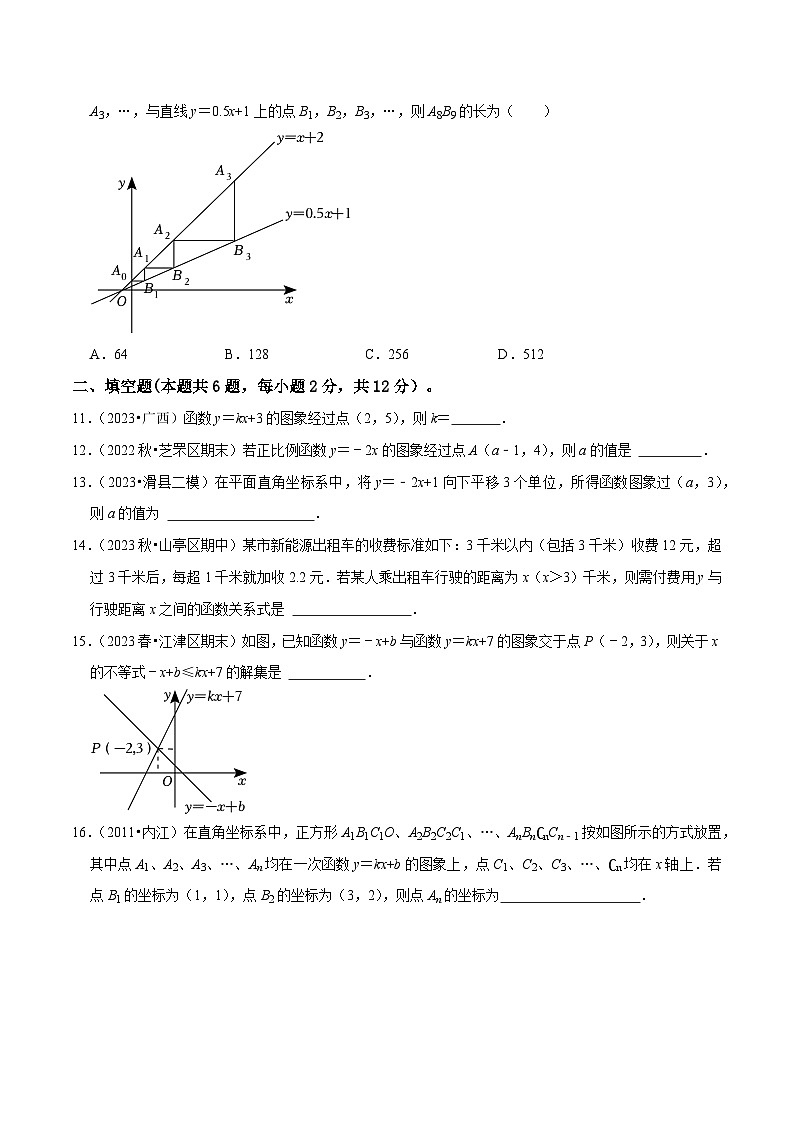
9．（2023秋•合肥期中）如图，已知一次函数y＝ax+b和y＝kx的图象相交于点P，则根据图象可得二元一次方程组的解是（ ）
A．B．C．D．
【答案】D
【解答】解：如图所示：根据图中信息可得二元一次方程组的解是：．
故选：D．
10．（2023春•盖州市期末）如图，直线y＝x+2与y轴相交于点A0，过点A0作x轴的平行线交直线y＝0.5x+1于点B1，过点B1作y轴的平行线交直线y＝x+2于点A1，再过点A1作x轴的平行线交直线y＝0.5x+1于点B2，过点B2作y轴的平行线交直线y＝x+2于点A2，…，依此类推，得到直线y＝x+2上的点A1，A2，A3，…，与直线y＝0.5x+1上的点B1，B2，B3，…，则A8B9的长为（ ）
A．64B．128C．256D．512
【答案】D
【解答】解：对于直线y＝x+2，令x＝0，求出y＝2，即A0（0，2），
∵A0B1∥x轴，∴B1的纵坐标为2，
将y＝2代入y＝0.5x+1中得：x＝2，即B1（2，2），
∴A0B1＝2＝21，
∵A1B1∥y轴，∴A1的横坐标为2，
将x＝2代入直线y＝x+2中得：y＝4，即A1（2，4），
∴A1与B2的纵坐标为4，
将y＝4代入y＝0.5x+1中得：x＝6，即B2（4，6），
∴A1B2＝4＝22，
同理A2B3＝8＝23，…，An﹣1Bn＝2n，
则A8B9的长为29＝512．
故选：D．
填空题(本题共6题，每小题2分，共12分）。
11．（2023•广西）函数y＝kx+3的图象经过点（2，5），则k＝ 1 ．
【答案】见试题解答内容
【解答】解：将点（2，5）代入y＝kx+3中，得5＝2k+3，
解得k＝1，
故答案为：1．
12．（2022秋•芝罘区期末）若正比例函数y＝﹣2x的图象经过点A（a﹣1，4），则a的值是 ﹣1 ．
【答案】见试题解答内容
【解答】解：∵正比例函数y＝﹣2x的图象经过点A（a﹣1，4），
∴4＝﹣2（a﹣1），解得：a＝﹣1．
故答案为：﹣1．
13．（2023•滑县二模）在平面直角坐标系中，将y＝﹣2x+1向下平移3个单位，所得函数图象过（a，3），则a的值为 ．
【答案】见试题解答内容
【解答】解：将y＝﹣2x+1向下平移3个单位得到y＝﹣2x﹣2，把（a，3）代入得到
3＝﹣2a﹣2，
解得，
故答案为：．
14．（2023秋•山亭区期中）某市新能源出租车的收费标准如下：3千米以内（包括3千米）收费12元，超过3千米后，每超1千米就加收2.2元．若某人乘出租车行驶的距离为x（x＞3）千米，则需付费用y与行驶距离x之间的函数关系式是 y＝2.2x+5.4 ．
【答案】见试题解答内容
【解答】解：由题意可得：y＝12+（x﹣3）×2.2
＝12+2.2x﹣6.6
＝5.4+2.2x．
故答案为：y＝2.2x+5.4．
15．（2023春•江津区期末）如图，已知函数y＝﹣x+b与函数y＝kx+7的图象交于点P（﹣2，3），则关于x的不等式﹣x+b≤kx+7的解集是 x≥﹣2 ．
【答案】x≥﹣2．
【解答】解：根据图象得当x≥﹣2时，﹣x+b≤kx+7．
故答案为：x≥﹣2．
16．（2011•内江）在直角坐标系中，正方形A1B1C1O、A2B2C2C1、…、AnBn∁nCn﹣1按如图所示的方式放置，其中点A1、A2、A3、…、An均在一次函数y＝kx+b的图象上，点C1、C2、C3、…、∁n均在x轴上．若点B1的坐标为（1，1），点B2的坐标为（3，2），则点An的坐标为 （2n﹣1﹣1，2n﹣1） ．
【答案】见试题解答内容
【解答】解：∵B1的坐标为（1，1），点B2的坐标为（3，2），
∴正方形A1B1C1O边长为1，正方形A2B2C2C1边长为2，
∴A1的坐标是（0，1），A2的坐标是：（1，2），
代入y＝kx+b得，
解得：．
则直线的解析式是：y＝x+1．
∵A1B1＝1，点B2的坐标为（3，2），
∴A1的纵坐标是1，A2的纵坐标是2．
在直线y＝x+1中，令x＝3，则纵坐标是：3+1＝4＝22；
则A4的横坐标是：1+2+4＝7，则A4的纵坐标是：7+1＝8＝23；
据此可以得到An的纵坐标是：2n﹣1，横坐标是：2n﹣1﹣1．
故点An的坐标为 （2n﹣1﹣1，2n﹣1）．
故答案为：（2n﹣1﹣1，2n﹣1）．
三、解答题（本题共7题，共58分）。
17．（2022秋•余姚市期末）已知y是x的一次函数，且当x＝﹣4时，y＝9；当x＝6时，y＝﹣1．
（1）求这个一次函数的解析式；
（2）当x＝时，求函数y的值；
（3）当﹣3＜y≤2时，求自变量x的取值范围．
【答案】（1）y＝﹣x+5；
（2）；
（3）3≤x＜8．
【解答】解：（1）设一次函数解析式为y＝kx+b，
把x＝﹣4，y＝9；x＝6，y＝﹣1分别代入得，
解得，
∴一次函数解析式为y＝﹣x+5；
（2）当x＝时，y＝﹣x+5＝﹣+5＝；
（3）当y＝﹣3时，﹣x+5＝﹣3，解得x＝8；
当y＝2时，﹣x+5＝2，解得x＝3，
∴当﹣3＜y≤2时，自变量x的取值范围为3≤x＜8．
18．（2023秋•蒲城县期中）已知一次函数y＝2x+4．
（1）画出该函数的图象；
（2）若该一次函数的图象与x轴交于点A，与y轴交于点B，求△OAB的面积．
【答案】（1）见解析图；
（2）4．
【解答】解：（1）∵一次函数y＝2x+4中，当x＝0时，y＝4；当y＝0时，x＝﹣2，
∴函数图象经过点（0，4），（﹣2，0）
函数图象如图．
（2）∵一次函数的图象与x轴交于点A，与y轴交于点B，
∴A（﹣2，0），B（0，4），
∴S△OAB＝OA•OB＝×2×4＝4．
19．（2023秋•陈仓区期中）如图，在平面直角坐标系中，点O为坐标原点，直线y＝kx+b经过A（﹣6，0），
B（0，3）两点，点C在直线AB上，C的纵坐标为4．
（1）求k、b的值及点C坐标；
（2）若点D为直线AB上一动点，且△OBC与△OAD的面积相等，试求点D的坐标．
【答案】（1）k＝，b＝3，C（2，4）；
（2）D（﹣4，1）或（﹣8，﹣1）．
【解答】解：（1）将A，B两点坐标代入y＝kx+b，
得，
解得，
∴直线解析式：y＝，
∵点C在直线AB上，C的纵坐标为4，
∴＝4，
解得x＝2，
∴k＝，b＝3，C（2，4）；
（2）∵B（0，3），
∴OB＝3，
∴S△OBC＝＝3，
∵A（﹣6，0），
∴OA＝6，
设△AOD中AO边上的高为h，
根据题意，得S△AOD＝＝3，
解得h＝1，
∴D点纵坐标为1或﹣1，
代入直线解析式，得＝1或＝﹣1，
解得x＝﹣4或﹣8，
∴D（﹣4，1）或（﹣8，﹣1）．
20．（2023秋•蒙城县期中）为了鼓励大家节约用电，某电力公司采取按月用电量分段收费，居民每月应交电费y（元）与用电量x（度）的函数图象是一条折线（如图所示），根据图像解答下列问题：
（1）求出y与x的函数关系式；
（2）若某用户某月用电80度，则应缴电费多少元？
（3）若某用户某月应缴电费105元，则该用户用了多少度电？
【答案】（1）；
（2）某用户某月用电80度，则应缴电费为52元；
（3）某用户某月应缴电费105元，则该用户用了150度电．
【解答】解：（1）当0≤x≤100时，设y＝kx，
将（100，65）代入得：65＝100k，
解得：k＝0.65，
∴y＝0.65x；
当x＞100时，设y＝ax+b，
将（100，65），（130，89）代入得：，
解得：，
∴y＝0.8x﹣15；
综上所述，y与x的函数关系式为；
（2）根据题意得：
在y＝0.65x中，当x＝80时，y＝0.65×80＝52，
∴某用户某月用电80度，则应缴电费为52元；
（3）∵105＞65，
∴令y＝0.8x﹣15＝105，
解得：x＝150，
∴某用户某月应缴电费105元，则该用户用了150度电．
21．（2023•青秀区校级模拟）某商店出售普通练习本和精装练习本，150本普通练习本和100精装练习本销售总额为1450元；200本普通练习本和50精装练习本销售总额为1100元．
（1）求普通练习本和精装练习本的销售单价分别是多少？
（2）该商店计划再次购进500本练习本，普通练习本的数量不低于精装练习本数量的3倍，已知普通练习本的进价为2元/个，精装练习本的进价为7元/个，设购买普通练习本x个，获得的利润为W元；
①求W关于x的函数关系式；
②该商店应如何进货才能使销售总利润最大？并求出最大利润．
【答案】见试题解答内容
【解答】解：（1）设普通练习本的销售单价为m元，精装练习本的销售单价为n元，
由题意可得：，
解得，
答：普通练习本的销售单价为3元，精装练习本的销售单价为10元；
（2）①购买普通练习本x个，则购买精装练习本（500﹣x）个，
由题意可得：W＝（3﹣2）x+（10﹣7）（500﹣x）＝﹣2x+1500，
∵普通练习本的数量不低于精装练习本数量的3倍，
∴x≥3（500﹣x），
解得x≥375，
即W关于x的函数关系式是；W＝﹣2x+1500（375≤x≤500）；
②∵W＝﹣2x+1500，
∴W随x的增大而减小，
∵375≤x≤500，
∴当x＝375时，W取得最大值，此时W＝750，500﹣x＝125，
答：当购买375个普通练习本，125个精装练习，销售总利润最大，最大总利润为750元．
22．（2022秋•遂川县期末）某校八年级学生外出社会实验活动，为了提前做好准备工作，学校安排小车送义工队前往，同时其余学生乘坐客车去目的地，小车到达目的地后立即返回，客车在目的地等候，如图是两车距学校的距离y（千米）与行驶时间x（小时）之间的函数图象．
（1）填空：目的地距离学校 180 千米，小车出发去目的地的行驶速度是 90 千米/时；
（2）当两车行驶3小时后在途中相遇，求点P的坐标；
（3）在第（2）题的条件下，求客车到达目的地所用时间．
【答案】见试题解答内容
【解答】解：（1）目的地距离学校180千米，小车出发去目的地的行驶速度是千米/时；
故答案为：180；90
（2）设直线AB的解析式是y＝kx+b，
因为A（2，180），B（5，0），可得：，
解得：．
所以可得AB 解析式：y＝﹣60x+300，
当 x＝3时，y＝120，
∴P（3，120）；
（3）直线OC解析式：y＝40x
当y＝180时，
即客车到达目的地所用时间为小时．
23．（2023春•洪洞县校级期末）如图一次函数y＝kx+b的图象经过点A（0，6），并与直线相交于点B，与x轴相交于点C，其中点B的横坐标为3．
（1）求一次函数y＝kx+b的表达式；
（2）点Q为直线y＝kx+b上一动点，当点Q运动到何位置时，△OBQ的面积等于？请求出点Q的坐标；
（3）在y轴上是否存在点P，使△PAB是等腰三角形？若存在，请直接写出点P的坐标；若不存在，请说明理由．
【答案】（1）；
（2）Q（4.5，3）或（1.5，5）；
（3）存在，或或（0，2）或．
【解答】解：（1）∵一次函数与相交于点B，其中点B的横坐标为3，
∴，
则点B（3，4），
将点A（0，6）、B（3，4）的坐标代入一次函数表达式y＝kx+b中，得，
解得：，b＝6，
所以一次函数的表达式为；
（2）设点，则△OBQ的面积＝，
解得：m＝4.5或1.5，
故点Q（4.5，3）或（1.5，5）；
（3）设点P（0，m），而点A、B的坐标分别为：（0，6），（3，4），
则AB2＝13，AP2＝（m﹣6）2，BP2＝9+（m﹣4）2，
当AB＝AP时，13＝（m﹣6）2，解得：或；
当AB＝BP时，同理可得：m＝6（舍去）或2；
当BP＝AP时，同理可得：；
综上点P的坐标为：或或（0，2）或．