2023-2024学年江苏省南京市宁海五十中学数学九上期末检测模拟试题含答案

这是一份2023-2024学年江苏省南京市宁海五十中学数学九上期末检测模拟试题含答案，共8页。

学校_______ 年级_______ 姓名_______
注意事项
1．考试结束后，请将本试卷和答题卡一并交回．
2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．
3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．
4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．
5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．
一、选择题（每题4分，共48分）
1．若抛物线y＝x2+bx+c与x轴只有一个公共点，且过点A(m，n），B(m﹣8，n)，则n的值为（ ）
A．8B．12C．15D．16
2．若抛物线y＝x2+ax+b与x轴两个交点间的距离为4，称此抛物线为定弦抛物线．已知某定弦抛物线的对称轴为直线x＝2，将此抛物线向左平移2个单位，再向上平移3个单位，得到的抛物线过点（ ）
A．（1，0）B．（1，8）C．（1，﹣1）D．（1，﹣6）
3．如图，平行于BC的直线DE把△ABC分成面积相等的两部分，则的值为（ ）
A．1B．C．-1D．+1
4．将二次函数的图象先向左平移1个单位，再向下平移2个单位，所得图象对应的函数表达式是（ ）
A．B．
C．D．
5．用配方法解方程配方正确的是（ ）
A．B．C．D．
6．要使方程是关于x的一元二次方程，则（ ）
A．a≠0B．a≠3
C．a≠3且b≠-1D．a≠3且b≠-1且c≠0
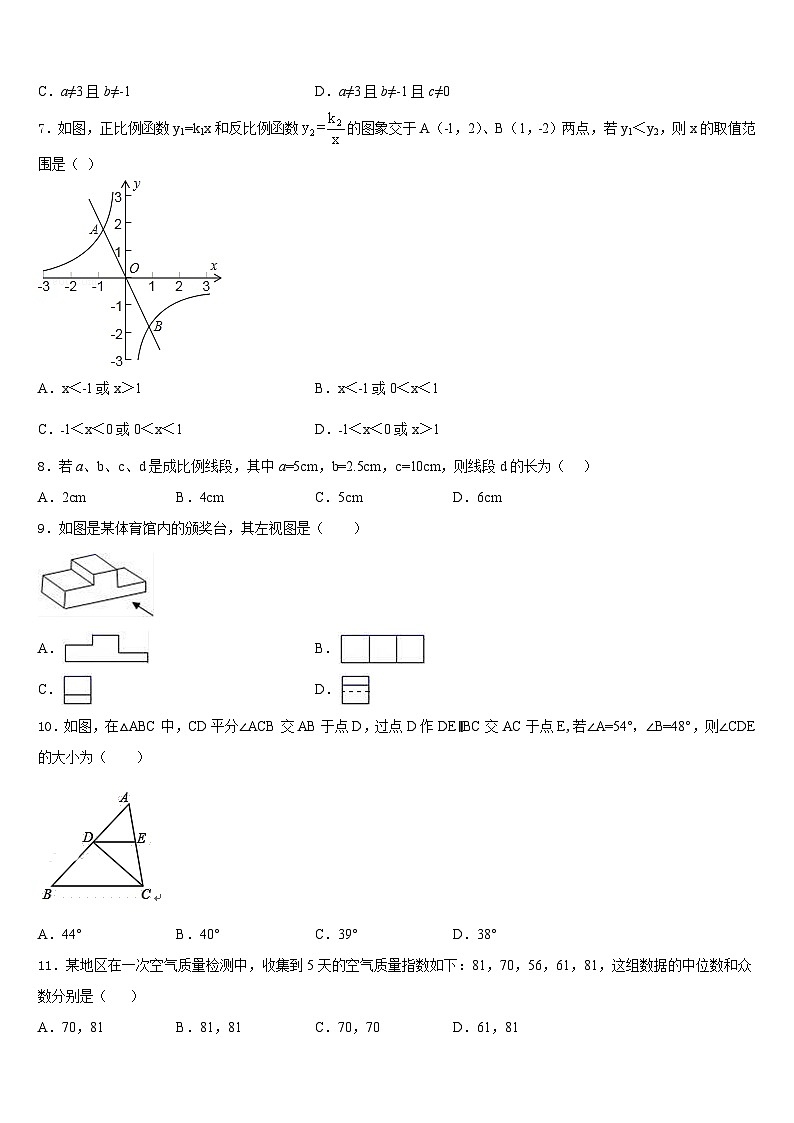
7．如图，正比例函数y1=k1x和反比例函数的图象交于A（﹣1，2）、B（1，﹣2）两点，若y1＜y2，则x的取值范围是（ ）
A．x＜﹣1或x＞1B．x＜﹣1或0＜x＜1
C．﹣1＜x＜0或0＜x＜1D．﹣1＜x＜0或x＞1
8．若a、b、c、d是成比例线段，其中a=5cm，b=2.5cm，c=10cm，则线段d的长为（ ）
A．2cmB．4cmC．5cmD．6cm
9．如图是某体育馆内的颁奖台，其左视图是（ ）
A．B．
C．D．
10．如图，在△ABC中，CD平分∠ACB交AB于点D，过点D作DE∥BC交AC于点E,若∠A=54°，∠B=48°，则∠CDE的大小为（ ）
A．44°B．40°C．39°D．38°
11．某地区在一次空气质量检测中，收集到5天的空气质量指数如下：81，70，56，61，81，这组数据的中位数和众数分别是（ ）
A．70，81B．81，81C．70，70D．61，81
12．为测量如图所示的斜坡垫的倾斜度，小明画出了斜坡垫的侧面示意图，测得的数据有：，则该斜坡垫的倾斜角 的正弦值是（ ）
A．B．C．D．
二、填空题（每题4分，共24分）
13．如图，矩形的对角线、相交于点，AB与BC的比是黄金比，过点C作CE∥BD，过点D作DE∥AC，DE、交于点，连接AE，则tan∠DAE的值为___________.（不取近似值）
14．如图，，，若，则_________ ．
15．微信给甲、乙、丙三人，若微信的顺序是任意的，则第一个微信给甲的概率为_____．
16．设、是关于的方程的两个根，则__________．
17．已知反比例函数y＝的图象位于第一、第三象限，则k的取值范围是_____．
18．如图，河的两岸、互相平行，点、、是河岸上的三点，点是河岸上一个建筑物，在处测得，在处测得，若米，则河两岸之间的距离约为______米（，结果精确到0.1米）（必要可用参考数据：）
三、解答题（共78分）
19．（8分）如图，已知反比例函数（k1＞0）与一次函数相交于A、B两点，AC⊥x轴于点C. 若△OAC的面积为1，且tan∠AOC＝2 .
（1）求出反比例函数与一次函数的解析式；
（2）请直接写出B点的坐标，并指出当x为何值时，反比例函数y1的值大于一次函数y2的值.
20．（8分）已知抛物线．
（1）当x为何值时，y随x的增大而减小；
（2）将该抛物线向右平移2个单位，再向上平移2个单位，请直接写出平移后的抛物线表达式．
21．（8分）如图，△ABC内接于⊙O，AB=AC=10，BC=12，点E是弧BC的中点.
(1)过点E作BC的平行线交AB的延长线于点D，求证：DE是⊙O的切线.
(2)点F是弧AC的中点，求EF的长.
22．（10分）瑞安市曹村镇“八百年灯会”成为温州“申遗”的宝贵项目．某公司生产了一种纪念花灯，每件纪念花灯制造成本为18元．设销售单价x（元），每日销售量y（件）每日的利润w（元）．在试销过程中，每日销售量y（件）、每日的利润w（元）与销售单价x（元）之间存在一定的关系，其几组对应量如下表所示：
（1）根据表中数据的规律，分别写出毎日销售量y（件），每日的利润w（元）关于销售单价x（元）之间的函数表达式．（利润＝（销售单价﹣成本单价）×销售件数）．
（2）当销售单价为多少元时，公司每日能够获得最大利润？最大利润是多少？
（3）根据物价局规定，这种纪念品的销售单价不得高于32元，如果公司要获得每日不低于350元的利润，那么制造这种纪念花灯每日的最低制造成本需要多少元？
23．（10分）综合与探究
如图，已知抛物线与轴交于，两点，与轴交于点，对称轴为直线，顶点为.
(1)求抛物线的解析式及点坐标；
(2)在直线上是否存在一点，使点到点的距离与到点的距离之和最小？若存在，求出点的坐标；若不存在，请说明理由.
(3)在轴上取一动点，，过点作轴的垂线，分别交抛物线，，于点，，.
①判断线段与的数量关系，并说明理由
②连接，，，当为何值时，四边形的面积最大？最大值为多少？
24．（10分）如图，是⊙的直径，是⊙的切线，点为切点，与⊙交于点，点是的中点，连结．
（1）求证：是⊙的切线；
（2）若，，求阴影部分的面积．
25．（12分）解方程：x2+11x+9＝1．
26．（12分）小明代表学校参加“我和我的祖国”主题宣传教育活动，该活动分为两个阶段，第一阶段有“歌曲演唱”、“书法展示”、“器乐独奏”3个项目（依次用、、表示），第二阶段有“故事演讲”、“诗歌朗诵”2个项目（依次用、表示），参加人员在每个阶段各随机抽取一个项目完成.
（1）用画树状图或列表的方法，列出小明参加项目的所有等可能的结果；
（2）求小明恰好抽中、两个项目的概率.
参考答案
一、选择题（每题4分，共48分）
1、D
2、A
3、C
4、B
5、A
6、B
7、D
8、C
9、D
10、C
11、A
12、A
二、填空题（每题4分，共24分）
13、
14、1
15、
16、1
17、.
18、54.6
三、解答题（共78分）
19、（1）；；（2）B点的坐标为（－2，－1）；当0＜x＜1和x＜－2时，y1＞y2.
20、（1）；（2）．
21、（1）见解析；（2）
22、（1）y＝﹣2x+100，w＝﹣2x2+136x﹣1800；（2）当销售单价为34元时，每日能获得最大利润，最大利润是1元；（3）制造这种纪念花灯每日的最低制造成本需要648元．
23、 (1)，点坐标为；(2)点的坐标为；(3)①；②当为-2时，四边形的面积最大，最大值为4.
24、（1）见解析；（2）．
25、x1＝﹣1，x2＝﹣2
26、（1）见解析；（2） .
（元）
19
20
21
30
（件）
62
60
58
40