
2023-2024学年广西壮族自治区河池市凤山县九上数学期末学业质量监测试题含答案
展开这是一份2023-2024学年广西壮族自治区河池市凤山县九上数学期末学业质量监测试题含答案,共8页。试卷主要包含了已知点等内容,欢迎下载使用。
学校_______ 年级_______ 姓名_______
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题(每题4分,共48分)
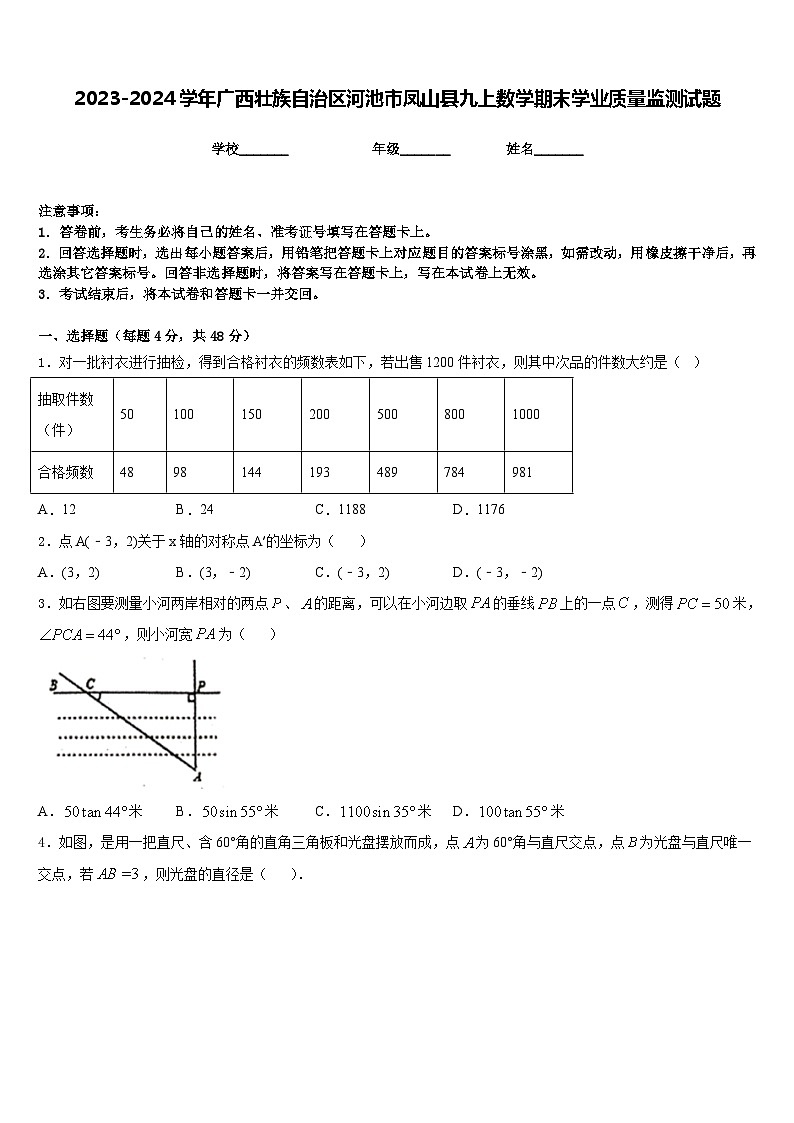
1.对一批衬衣进行抽检,得到合格衬衣的频数表如下,若出售1200件衬衣,则其中次品的件数大约是( )
A.12B.24C.1188D.1176
2.点A(﹣3,2)关于x轴的对称点A′的坐标为( )
A.(3,2)B.(3,﹣2)C.(﹣3,2)D.(﹣3,﹣2)
3.如右图要测量小河两岸相对的两点、的距离,可以在小河边取的垂线上的一点,测得米,,则小河宽为( )
A.米B.米C.米D.米
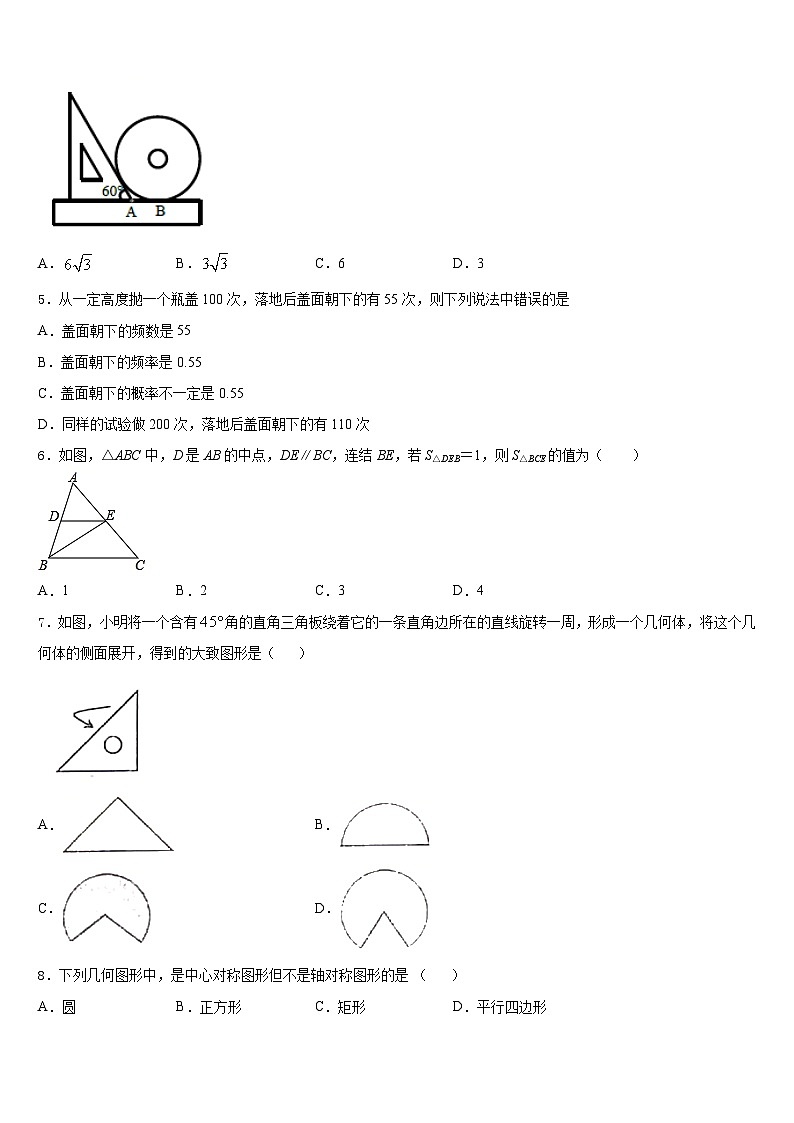
4.如图,是用一把直尺、含60°角的直角三角板和光盘摆放而成,点为60°角与直尺交点,点为光盘与直尺唯一交点,若,则光盘的直径是( ).
A.B.C.6D.3
5.从一定高度抛一个瓶盖100次,落地后盖面朝下的有55次,则下列说法中错误的是
A.盖面朝下的频数是55
B.盖面朝下的频率是0.55
C.盖面朝下的概率不一定是0.55
D.同样的试验做200次,落地后盖面朝下的有110次
6.如图,△ABC中,D是AB的中点,DE∥BC,连结BE,若S△DEB=1,则S△BCE的值为( )
A.1B.2C.3D.4
7.如图,小明将一个含有角的直角三角板绕着它的一条直角边所在的直线旋转一周,形成一个几何体,将这个几何体的侧面展开,得到的大致图形是( )
A.B.
C.D.
8.下列几何图形中,是中心对称图形但不是轴对称图形的是 ( )
A.圆B.正方形C.矩形D.平行四边形
9.已知点(3,﹣4)在反比例函数的图象上,则下列各点也在该反比例函数图象上的是( )
A.(3,4)B.(﹣3,﹣4)C.(﹣2,6)D.(2,6)
10.若关于x的一元二次方程kx2﹣2x+1=0有两个不相等的实数根,则实数k的取值范围是( )
A.k>1B.k<1C.k>1且k≠0D.k<1且k≠0
11.若关于x的一元二次方程有实数根,则实数k的取值范围为
A.,且B.,且
C.D.
12.如图,已知在△ABC纸板中,AC=4,BC=8,AB=11,P是BC上一点,沿过点P的直线剪下一个与△ABC相似的小三角形纸板,如果有4种不同的剪法,那么CP长的取值范围是( )
A.0<CP≤1B.0<CP≤2C.1≤CP<8D.2≤CP<8
二、填空题(每题4分,共24分)
13.某一时刻身高160cm的小王在太阳光下的影长为80cm,此时他身旁的旗杆影长10m,则旗杆高为______.
14.在中,,点、分别在边、上,,(如图),沿直线翻折,翻折后的点落在内部的点,直线与边相交于点,如果,那么__________.
15.如图,从甲楼底部A处测得乙楼顶部C处的仰角是30°,从甲楼顶部B处测得乙楼底部D处的俯角是45°,已知甲楼的高AB是120m,则乙楼的高CD是_____m(结果保留根号)
16.如图,△ABC内接于⊙O,∠ACB=35º,则∠OAB= º.
17.如图,在中,,,,将绕点逆时针旋转得到,连接,则的长为__________.
18.已知圆锥的底面半径为3,母线长为7,则圆锥的侧面积是_____.
三、解答题(共78分)
19.(8分)如图,AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E,已知AB=2DE,∠E=18°,求∠AOC的度数.
20.(8分)阅读下面材料,完成(1)﹣(3)题
数学课上,老师出示了这样一道题:如图,四边形ABCD,AD∥BC,AB=AD,E为对角线AC上一点,∠BEC=∠BAD=2∠DEC,探究AB与BC的数量关系.
某学习小组的同学经过思考,交流了自己的想法:
小柏:“通过观察和度量,发现∠ACB=∠ABE”;
小源:“通过观察和度量,AE和BE存在一定的数量关系”;
小亮:“通过构造三角形全等,再经过进一步推理,就可以得到线段AB与BC的数量关系”.
……
老师:“保留原题条件,如图2, AC上存在点F,使DF=CF=AE,连接DF并延长交BC于点G,求的值”.
(1)求证:∠ACB=∠ABE;
(2)探究线段AB与BC的数量关系,并证明;
(3)若DF=CF=AE,求的值(用含k的代数式表示).
21.(8分)在的方格纸中,的三个顶点都在格点上.
在图1中画出线段BD,使,其中D是格点;
在图2中画出线段BE,使,其中E是格点.
22.(10分)如图,在中,,.
(1)在边上求作一点,使得.(要求:尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,求证:为线段的黄金分割点.
23.(10分)如图,是圆的直径,点在圆上,分别连接、,过点作直线,使.求证:直线与圆相切.
24.(10分)某小型工厂9月份生产的、两种产品数量分别为200件和100件,、两种产品出厂单价之比为2:1,由于订单的增加,工厂提高了、两种产品的生产数量和出厂单价,10月份产品生产数量的增长率和产品出厂单价的增长率相等,产品生产数量的增长率是产品生产数量的增长率的一半,产品出厂单价的增长率是产品出厂单价的增长率的2倍,设产品生产数量的增长率为(),若10月份该工厂的总收入增加了,求的值.
25.(12分)已知直线与是的直径,于点.
(1)如图①,当直线与相切于点时,若,求的大小;
(2)如图②,当直线与相交于点时,若,求的大小.
26.(12分)已知抛物线.
(1)当x为何值时,y随x的增大而减小;
(2)将该抛物线向右平移2个单位,再向上平移2个单位,请直接写出平移后的抛物线表达式.
参考答案
一、选择题(每题4分,共48分)
1、B
2、D
3、A
4、A
5、D
6、B
7、C
8、D
9、C
10、D
11、A
12、B
二、填空题(每题4分,共24分)
13、20m
14、
15、40
16、55
17、1
18、21π.
三、解答题(共78分)
19、54°.
20、(1)见解析;(2)CB=2AB;(3)
21、(1)画图见解析;(2)画图见解析.
22、(1)见解析;(2)证明见解析.
23、见解析
24、5%
25、(1)30°;(2)18°
26、(1);(2).
抽取件数(件)
50
100
150
200
500
800
1000
合格频数
48
98
144
193
489
784
981
相关试卷
这是一份2023-2024学年林芝九上数学期末学业质量监测模拟试题含答案,共7页。试卷主要包含了的倒数是,点P,关于的一元二次方程的根的情况是等内容,欢迎下载使用。
这是一份2023-2024学年广西壮族自治区河池市罗城仫佬族自治县数学九上期末学业质量监测试题含答案,共7页。试卷主要包含了某反比例函数的图象经过点等内容,欢迎下载使用。
这是一份2023-2024学年广西河池市环江县数学九上期末学业质量监测模拟试题含答案,共8页。试卷主要包含了一元二次方程有实数解的条件,抛物线如图所示,给出以下结论等内容,欢迎下载使用。












