2023-2024学年山东省青岛西海岸新区第四中学九年级数学第一学期期末学业质量监测试题含答案

这是一份2023-2024学年山东省青岛西海岸新区第四中学九年级数学第一学期期末学业质量监测试题含答案，共8页。试卷主要包含了考生必须保证答题卡的整洁，关于x的一元二次方程等内容，欢迎下载使用。
学校_______ 年级_______ 姓名_______
注意事项：
1．答卷前，考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用2B铅笔将试卷类型（B）填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。
2．作答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。答案不能答在试题卷上。
3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。不按以上要求作答无效。
4．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。
一、选择题（每题4分，共48分）
1．如图，已知，M，N分别为锐角∠AOB的边OA，OB上的点，ON=6，把△OMN沿MN折叠，点O落在点C处，MC与OB交于点P，若MN=MP=5，则PN=( )
A．2B．3C．D．
2．方程是关于的一元二次方程，则的值不能是（ ）
A．0B．C．D．
3．如图，将一副三角板如图放置，如果，那么点到的距离为( )
A．B．C．D．
4．如图，小明利用测角仪和旗杆的拉绳测量学校旗杆的高度．如图，旗杆PA的高度与拉绳PB的长度相等．小明将PB拉到PB′的位置，测得∠PB′C＝α(B′C为水平线)，测角仪B′D的高度为1m，则旗杆PA的高度为( )
A．mB．mC． mD． m
5．二次函数y=ax2+bx+c（a，b，c为常数且a≠0）的图象如图所示，则一次函数y=ax+b与反比例函数的图象可能是
A．B．C．D．
6．下列图形中，既是轴对称图形，又是中心对称图形的是（ ）
A．B．
C．D．
7．分别以等边三角形的三个顶点为圆心，以边长为半径画弧，得到封闭图形就是莱洛三角形，如图，已知等边，，则该莱洛三角形的面积为（ ）
A．B．C．D．
8．关于x的一元二次方程（m﹣1）x2+x+m2﹣1＝0的一个根为0，则m为（ ）
A．0B．1C．﹣1D．1或﹣1
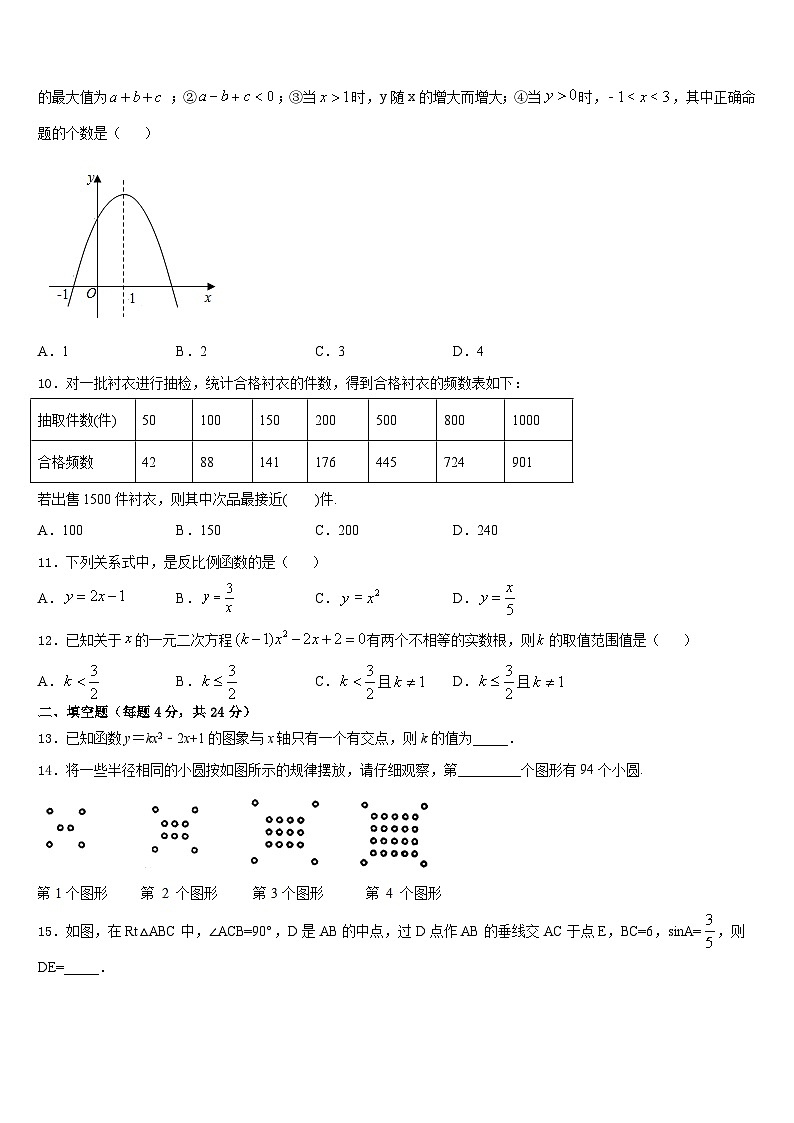
9．如图，若二次函数的图象的对称轴为，与x轴的一个交点为，则：①二次函数的最大值为 ；②；③当时，y随x的增大而增大；④当时，，其中正确命题的个数是（ ）
A．1B．2C．3D．4
10．对一批衬衣进行抽检，统计合格衬衣的件数，得到合格衬衣的频数表如下：
若出售1500件衬衣，则其中次品最接近( )件.
A．100B．150C．200D．240
11．下列关系式中，是反比例函数的是（ ）
A．B．C．D．
12．已知关于的一元二次方程有两个不相等的实数根，则的取值范围值是（ ）
A．B．C．且D．且
二、填空题（每题4分，共24分）
13．已知函数y＝kx2﹣2x+1的图象与x轴只有一个有交点，则k的值为_____．
14．将一些半径相同的小圆按如图所示的规律摆放，请仔细观察，第_________个图形有94个小圆.
15．如图，在Rt△ABC中，∠ACB=90°，D是AB的中点，过D点作AB的垂线交AC于点E，BC=6，sinA=，则DE=_____．
16．如图，在网格中，小正方形的边长均为1，点A、B、O都在格点上，则∠OAB的正弦值是_____．
17．已知两个二次函数的图像如图所示，那么 a1________a2（填“＞”、“＝”或“＜”）．
18．为准备体育中考，甲、乙两名学生各进行了10次1分钟跳绳的测试，已知两名学生10次1分钟跳绳的平均成绩均为160个，甲的方差是80（个），乙的方差是100（个）.则这10次1分钟跳绳测试成绩比较稳定的学生是________ （填“甲”或“乙”）.
三、解答题（共78分）
19．（8分）某商场经营某种品牌的玩具，购进时的单价是30元，根据市场调查：在一段时间内，销售单价是40元时，销售量是600件，而销售单价每涨1元，就会少售出10件玩具．
（1）不妨设该种品牌玩具的销售单价为x元（x＞40），请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元，并把结果填写在表格中：
（2）在（1）问条件下，若商场获得了10000元销售利润，求该玩具销售单价x应定为多少元．
（3）在（1）问条件下，若玩具厂规定该品牌玩具销售单价不低于44元，且商场要完成不少于540件的销售任务，求商场销售该品牌玩具获得的最大利润是多少？
20．（8分）在平面直角坐标系中，已知抛物线y＝x2+kx+c的图象经过点C（0，1），当x＝2时，函数有最小值．
（1）求抛物线的解析式；
（2）直线l⊥y轴，垂足坐标为（0，﹣1），抛物线的对称轴与直线l交于点A．在x轴上有一点B，且AB＝，试在直线l上求异于点A的一点Q，使点Q在△ABC的外接圆上；
（3）点P（a，b）为抛物线上一动点，点M为坐标系中一定点，若点P到直线l的距离始终等于线段PM的长，求定点M的坐标．
21．（8分）已知关于x的一元二次方程.
（1）求证：方程有两个不相等的实数根；
（2）如果方程的两实根为，，且，求m的值．
22．（10分）已知抛物线y＝kx2+（1﹣2k）x+1﹣3k与x轴有两个不同的交点A、B．
（1）求k的取值范围；
（2）证明该抛物线一定经过非坐标轴上的一点M，并求出点M的坐标；
（3）当＜k≤8时，由（2）求出的点M和点A，B构成的△ABM的面积是否有最值？若有，求出该最值及相对应的k值．
23．（10分）在平面直角坐标系中的位置如图所示.
在图中画出关于轴对称的图形，并写出顶点的坐标；
将向下平移个单位长度，再向左平移个单位长度得到，画出平移后的，并写出顶点的坐标.
24．（10分）如图，把一个木制正方体的表面涂上颜色，然后将正方体分割成64个大小相同的小正方体．从这些小正方体中任意取出一个，求取出的小正方体：
（1）三面涂有颜色的概率；
（2）两面涂有颜色的概率；
（3）各个面都没有颜色的概率．
25．（12分）如图，在Rt△ABC中，∠C＝90°，BC＝5，AC＝12，求∠A的正弦值、余弦值和正切值．
26．（12分）我们不妨约定：如图①，若点D在△ABC的边AB上，且满足∠ACD=∠B（或∠BCD=∠A），则称满足这样条件的点为△ABC边AB上的“理想点”．
（1）如图①，若点D是△ABC的边AB的中点，AC=，AB=4.试判断点D是不是△ABC边AB上的“理想点”，并说明理由．
（2）如图②，在⊙O中，AB为直径，且AB=5，AC=4.若点D是△ABC边AB上的“理想点”，求CD的长．
（3）如图③，已知平面直角坐标系中，点A(0,2),B(0,-3),C为x轴正半轴上一点，且满足∠ACB=45°，在y轴上是否存在一点D，使点A是B，C，D三点围成的三角形的“理想点”，若存在，请求出点D的坐标；若不存在，请说明理由．
参考答案
一、选择题（每题4分，共48分）
1、D
2、C
3、B
4、A
5、C
6、C
7、D
8、C
9、B
10、B
11、B
12、C
二、填空题（每题4分，共24分）
13、0或1．
14、9.
15、
16、
17、
18、甲
三、解答题（共78分）
19、 (1) 1000﹣x，﹣10x2+1300x﹣1；（2）50元或80元；（3）8640元.
20、（1）y＝x2﹣x+1； （2）Q（1，﹣1）；（3）M（2，1）
21、（1）证明见解析（1）1或1
22、（1）且；（2）见解析，M(3,4) ；（3）△ABM的面积有最大值，
23、（1）作图见解析，；（2）作图见解析，
24、（1）；（2）；（3）
25、sinA=，csA=，tanA=．
26、（1）是，理由见解析；（2）；（3）D（0,42）或D（0,6）
抽取件数(件)
50
100
150
200
500
800
1000
合格频数
42
88
141
176
445
724
901
销售单价（元）
x
销售量y（件）

销售玩具获得利润w（元）