浙江省杭州市高桥2023-2024学年九年级数学第一学期期末达标检测试题含答案

这是一份浙江省杭州市高桥2023-2024学年九年级数学第一学期期末达标检测试题含答案，共8页。试卷主要包含了考生必须保证答题卡的整洁，如图，，若，则的长是等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
考生请注意：
1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。
2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。
3．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1．方程x2+4x+4＝0的根的情况是（ ）
A．有两个不相等的实数根B．有两个相等的实数根
C．有一个实数根D．没有实数根
2．已知a、b、c、d是比例线段．a=2、b=3、d=1．那么c等于（ ）
A．9B．4C．1D．12
3．如图是二次函数图象的一部分，其对称轴是，且过点，下列说法：①；②；③；④若是抛物线上两点，则，其中说法正确的是（ ）
A．①②B．②③C．①②④D．②③④
4．如图，四边形ABCD内接于，如果它的一个外角∠DCE=64°，那么∠BOD=（ ）
A．128°B．100°C．64°D．32°
5．从这七个数中随机抽取一个数记为，则的值是不等式组的解，但不是方程的实数解的概率为（ ）．
A．B．C．D．
6．要制作两个形状相同的三角形框架，其中一个三角形的三边长分别为5，6，9，另一个三角形的最长边长为4.5，则它的最短边长是（ ）
A．B．C．D．
7．在下列四个图案中，既是轴对称图形，又是中心对称图形的是( )
A．B．C．D．
8．向上发射一枚炮弹，经秒后的高度为，且时间与高度的关系式为，若此时炮弹在第秒与第秒时的高度相等，则在下列哪一个时间的高度是最高的（ ）
A．第秒B．第秒C．第秒D．第秒
9．如图，AB是⊙O的弦，OD⊥AB于D交⊙O于E，则下列说法错误的是( )
A．AD=BDB．∠ACB=∠AOEC．弧AE=弧BED．OD=DE
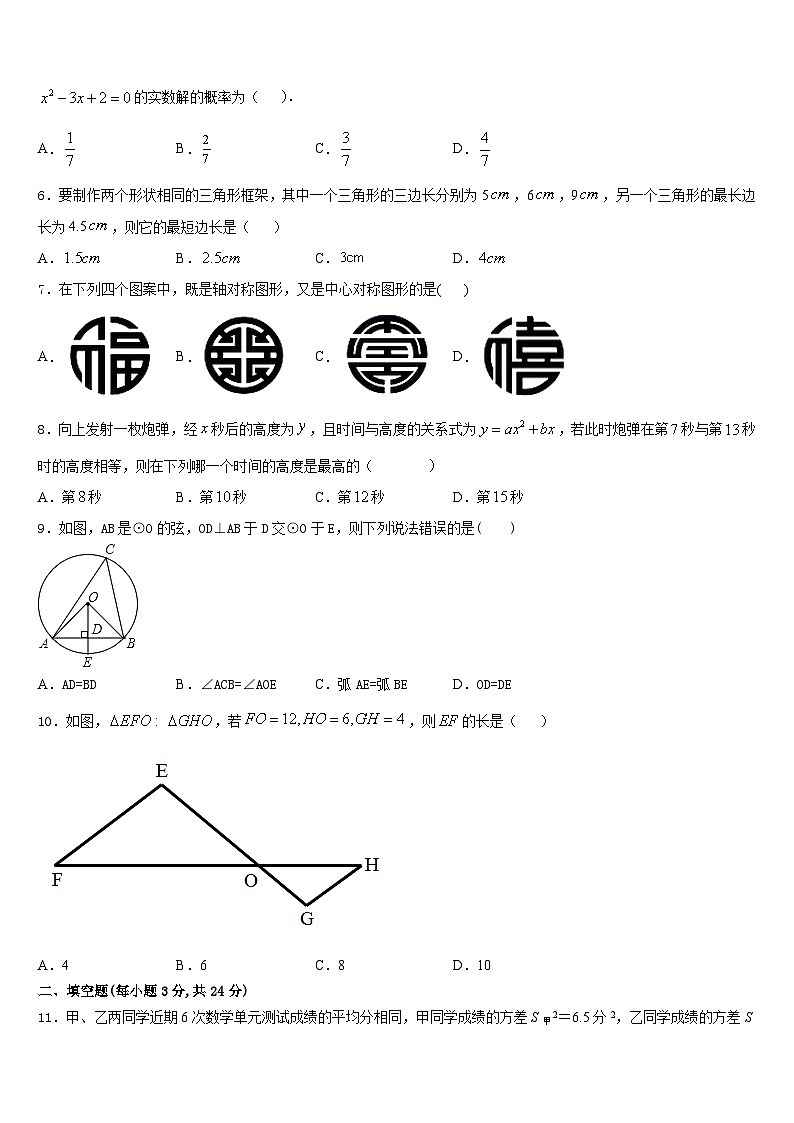
10．如图，，若，则的长是（ ）
A．4B．6C．8D．10
二、填空题(每小题3分,共24分)
11．甲、乙两同学近期6次数学单元测试成绩的平均分相同，甲同学成绩的方差S甲2＝6.5分2，乙同学成绩的方差S乙2＝3.1分2，则他们的数学测试成绩较稳定的是____（填“甲”或“乙”）．
12．菱形有一个内角为60°，较短的对角线长为6，则它的面积为_____．
13．一个密码箱的密码，每个数位上的数都是从0到9的自然数，若要使一次拨对的概率小于，则密码的位数至少要设置___位．
14．掷一枚硬币三次，正面都朝上的概率是__________．
15．为准备体育中考，甲、乙两名学生各进行了10次1分钟跳绳的测试，已知两名学生10次1分钟跳绳的平均成绩均为160个，甲的方差是80（个），乙的方差是100（个）.则这10次1分钟跳绳测试成绩比较稳定的学生是________ （填“甲”或“乙”）.
16．如图，点的坐标为，过点作轴的垂线交过原点与轴夹角为的直线于点，以原点为圆心，的长为半径画弧交轴正半轴于点；再过点作轴的垂线交直线于点，以原点为圆心，以的长为半径画弧交轴正半轴于点……按此做法进行下去，则点的坐标是_____．
17．如图所示的网格是正方形网格，线段AB绕点A顺时针旋转α（0°＜α＜180°）后与⊙O相切，则α的值为_____．
18．如图，在中，点是边的中点，⊙经过、、三点，交于点，是⊙的直径，是上的一个点，且，则___________．
三、解答题(共66分)
19．（10分）如图，坡AB的坡比为1：2.4，坡长AB=130米，坡AB的高为BT．在坡AB的正面有一栋建筑物CH，点H、A、T在同一条地平线MN上．
（1）试问坡AB的高BT为多少米？
（2）若某人在坡AB的坡脚A处和中点D处，观测到建筑物顶部C处的仰角分别为60°和30°，试求建筑物的高度CH．（精确到米，≈1.73，≈1.41）
20．（6分）如图，抛物线y1＝a（x﹣1）2+4与x轴交于A（﹣1，0）．
（1）求该抛物线所表示的二次函数的表达式；
（2）一次函数y2＝x+1的图象与抛物线相交于A，C两点，过点C作CB垂直于x轴于点B，求△ABC的面积．
21．（6分）如图，AB为⊙O的直径，C为⊙O上一点，D为的中点．过点D作直线AC的垂线，垂足为E，连接OD．
（1）求证：∠A=∠DOB；
（2）DE与⊙O有怎样的位置关系？请说明理由．
22．（8分）如图所示，在中，点在边上，联结，，交边于点，交延长线于点，且.
（1）求证：；
（2）求证：.
23．（8分）解方程
（1）（x+1）2﹣25＝0
（2）x2﹣4x﹣2＝0
24．（8分）如图所示，在矩形OABC中，OA=5，AB=4，点D为边AB上一点，将△BCD沿直线CD折叠，使点B恰好落在OA边上的点E处，分别以OC，OA所在的直线为x轴，y轴建立平面直角坐标系．
（1）求OE的长．
（2）求经过O，D，C三点的抛物线的解析式．
（3）一动点P从点C出发，沿CB以每秒2个单位长的速度向点B运动，同时动点Q从E点出发，沿EC以每秒1个单位长的速度向点C运动，当点P到达点B时，两点同时停止运动．设运动时间为t秒，当t为何值时，DP=DQ．
（4）若点N在（2）中的抛物线的对称轴上，点M在抛物线上，是否存在这样的点M与点N，使得以M，N，C，E为顶点的四边形是平行四边形？若存在，直接写出M点的坐标；若不存在，请说明理由．
25．（10分）如图，在矩形ABCD中，AB=10，动点E、F分别在边AB、AD上，且AF=AE．将△AEF绕点E顺时针旋转10°得到△A'EF'，设AE=x，△A'EF'与矩形ABCD重叠部分面积为S，S的最大值为1．
（1）求AD的长；
（2）求S关于x的函数解析式，并写出自变量x的取值范围．
26．（10分）（1）解方程
（2）计算：
参考答案
一、选择题(每小题3分,共30分)
1、B
2、B
3、A
4、A
5、B
6、B
7、B
8、B
9、D
10、C
二、填空题(每小题3分,共24分)
11、乙
12、18
13、1．
14、
15、甲
16、
17、60°或120 °
18、1
三、解答题(共66分)
19、（1）坡AB的高BT为50米；（2）建筑物高度为89米
20、（1）y1＝﹣（x﹣1）2+4；（2）.
21、（1）见解析；（2）相切，理由见解析
22、（1）见解析；（2）见解析.
23、（1）x1＝4，x2＝﹣6；（2）x1＝2+，x2＝2﹣
24、（1）3；（2）；（3）t=；（1）存在，M点的坐标为（2,16）或（-6,16）或
25、（1）；（2）
26、（1），；（2）