周口市重点中学2023-2024学年九年级数学第一学期期末学业质量监测模拟试题含答案

这是一份周口市重点中学2023-2024学年九年级数学第一学期期末学业质量监测模拟试题含答案，共8页。试卷主要包含了在中， ，则等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
注意事项
1．考试结束后，请将本试卷和答题卡一并交回．
2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．
3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．
4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．
5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．
一、选择题(每小题3分,共30分)
1．如图，在正方形ABCD中，G为CD边中点，连接AG并延长，分别交对角线BD于点F，交BC边延长线于点E．若FG＝2，则AE的长度为( )
A．6B．8
C．10D．12
2．如图所示，抛物线y＝ax2+bx+c(a≠0)的对称轴为直线x＝1，与y轴的一个交点坐标为(0，3)，其部分图象如图所示，下列结论：①abc＜0；②4a+c＞0；③方程ax2+bx+c＝3的两个根是x1＝0，x2＝2；④方程ax2+bx+c＝0有一个实根大于2；⑤当x＜0时，y随x增大而增大．其中结论正确的个数是（ ）
A．4个B．3个C．2个D．1个
3．下列多边形一定相似的是（ ）
A．两个平行四边形B．两个矩形
C．两个菱形D．两个正方形
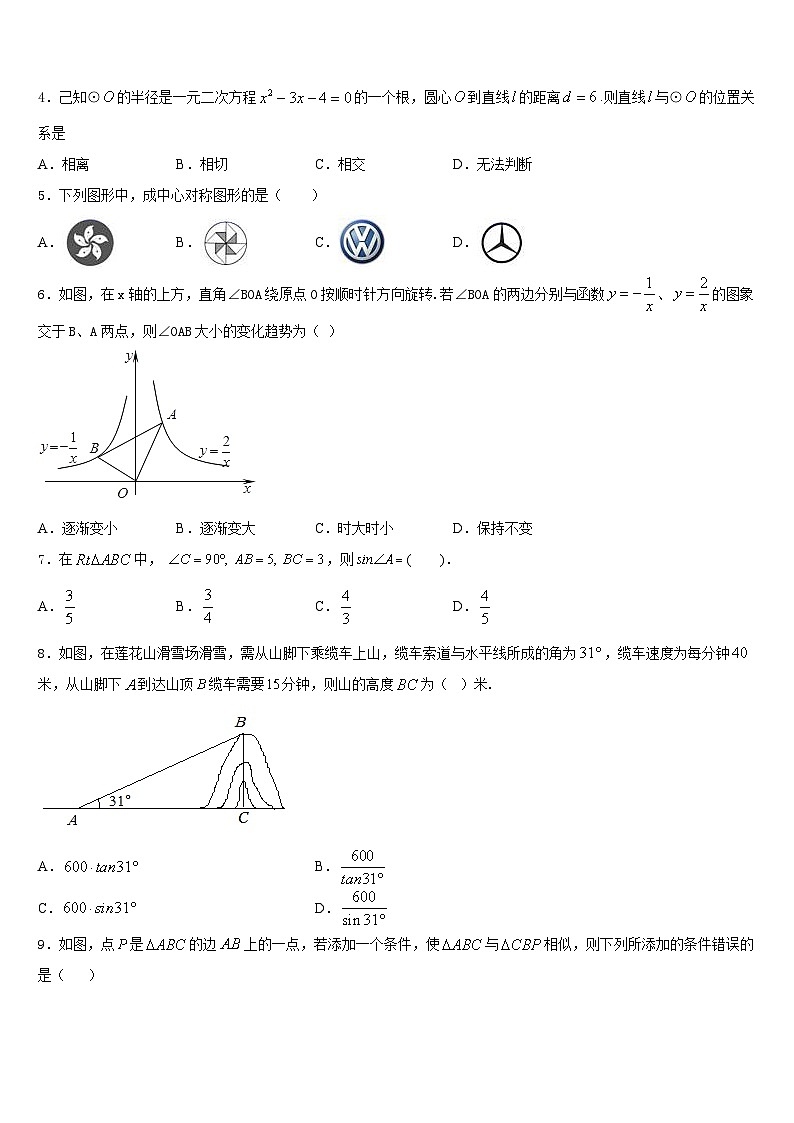
4．己知⊙的半径是一元二次方程的一个根，圆心到直线的距离.则直线与⊙的位置关系是
A．相离B．相切C．相交D．无法判断
5．下列图形中，成中心对称图形的是（ ）
A．B．C．D．
6．如图，在x轴的上方，直角∠BOA绕原点O按顺时针方向旋转.若∠BOA的两边分别与函数、的图象交于B、A两点，则∠OAB大小的变化趋势为（ ）
A．逐渐变小B．逐渐变大C．时大时小D．保持不变
7．在中， ，则( )．
A．B．C．D．
8．如图，在莲花山滑雪场滑雪，需从山脚下乘缆车上山，缆车索道与水平线所成的角为，缆车速度为每分钟米，从山脚下到达山顶缆车需要分钟，则山的高度为（ ）米.
A．B．
C．D．
9．如图，点是的边上的一点，若添加一个条件，使与相似，则下列所添加的条件错误的是（ ）
A．B．C．D．
10．下列光线所形成的投影不是中心投影的是（ ）
A．太阳光线B．台灯的光线C．手电筒的光线D．路灯的光线
二、填空题(每小题3分,共24分)
11．直线y＝2被抛物线y＝x2﹣3x+2截得的线段长为_____．
12．已 知二次函数 y =ax2－bx＋2(a ≠0) 图象的顶点在第二象限，且过点（1，0），则a的取值范围是 _________；若a＋b 的值为非零整数，则 b 的值为 _________．
13．如图，在△ABC中，AC：BC：AB＝3：4：5，⊙O沿着△ABC的内部边缘滚动一圈，若⊙O的半径为1，且圆心O运动的路径长为18，则△ABC的周长为_____．
14．如图，在扇形AOB中，∠AOB=90°，点C为OA的中点，CE⊥OA交于点E，以点O为圆心，OC的长为半径作交OB于点D，若OA=2，则阴影部分的面积为 .
15．如图，菱形ABCD的边AD与x轴平行，A、B两点的横坐标分别为1和3，反比例函数y＝的图象经过A、B两点，则菱形ABCD的面积是_____；
16．在中，，，，圆在内自由移动.若的半径为1，则圆心在内所能到达的区域的面积为______.
17．在一个不透明的袋子中有个红球、个绿球和个白球，这些球除颜色外都相同，摇匀后从袋子中任意摸出一个球，摸出_______颜色的球的可能性最大.
18．若有一组数据为8、4、5、2、1，则这组数据的中位数为__________．
三、解答题(共66分)
19．（10分）（1）用配方法解方程：；
（2）用公式法解方程：.
20．（6分）综合与实践：
如图，已知 中,．
（1）实践与操作： 作 的外接圆，连结 ，并在图中标明相应字母；（尺规作图，保留作图痕迹， 不写作法）
（2）猜想与证明： 若，求扇形的面积.
21．（6分）已知抛物线y＝x2﹣2x﹣3与x轴交于点A、B，与y轴交于点C，点D为OC中点，点P在抛物线上．
（1）直接写出A、B、C、D坐标；
（2）点P在第四象限，过点P作PE⊥x轴，垂足为E，PE交BC、BD于G、H，是否存在这样的点P，使PG＝GH＝HE？若存在，求出点P坐标；若不存在，请说明理由．
（3）若直线y＝x+t与抛物线y＝x2﹣2x﹣3在x轴下方有两个交点，直接写出t的取值范围．
22．（8分）已知，在△ABC中，∠BAC=90°，∠ABC=45°，点D为直线BC上一动点（点D不与点B，C重合）．以AD为边做正方形ADEF，连接CF
（1）如图1，当点D在线段BC上时．求证CF+CD=BC；
（2）如图2，当点D在线段BC的延长线上时，其他条件不变，请直接写出CF，BC，CD三条线段之间的关系；
（3）如图3，当点D在线段BC的反向延长线上时，且点A，F分别在直线BC的两侧，其他条件不变；
①请直接写出CF，BC，CD三条线段之间的关系；
②若正方形ADEF的边长为，对角线AE，DF相交于点O，连接OC．求OC的长度．
23．（8分）如图，是的直径，点在上，平分，是的切线，与相交于点，与相交于点，连接．

（1）求证：；
（2）若，，求的长．
24．（8分）如图，在一条河流的两岸分别有A、B、C、D四棵景观树，已知AB//CD，某数学活动小组测得∠DAB=45°，∠CBE=73°，AB=10m，CD=30m，请计算这条河的宽度(参考数值：，，)
25．（10分）如图，建筑物AB的高为6cm，在其正东方向有个通信塔CD，在它们之间的地面点M（B，M，D三点在一条直线上）处测得建筑物顶端A、塔项C的仰角分别为37°和60°，在A处测得塔顶C的仰角为30°，则通信塔CD的高度．（sin37°≈0.60，cs37°≈0.80，tan37°≈0.75，=1.73，精确到0.1m）
26．（10分）如图，△ABC的中线AD、BE、CF相交于点G，H、I分别是BG、CG的中点．
（1）求证：四边形EFHI是平行四边形；
（2）①当AD与BC满足条件 时，四边形EFHI是矩形；
②当AG与BC满足条件 时，四边形EFHI是菱形．
参考答案
一、选择题(每小题3分,共30分)
1、D
2、A
3、D
4、A
5、B
6、D
7、A
8、C
9、D
10、A
二、填空题(每小题3分,共24分)
11、1
12、
13、4
14、.
15、
16、24
17、白
18、4
三、解答题(共66分)
19、（1）；；（2）；
20、（1）答案见解析；（2）
21、（1）A(﹣1，0)，B(3，0)，C(0，﹣3)，D(0，﹣)；（2）存在，(，﹣)；（3）﹣＜t＜﹣1
22、（1）证明见解析；（1）CF﹣CD=BC；（3）①CD﹣CF=BC；②1．
23、（1）见解析；（2）
24、m
25、通信塔CD的高度约为15.9cm．
26、（1）证明见解析；（2）①AD⊥BC；②2AD=3BC