中职数学高教版（2021）基础模块下册9.5 柱、锥、球及简单组合体获奖备课教学课件ppt

这是一份中职数学高教版（2021）基础模块下册9.5 柱、锥、球及简单组合体获奖备课教学课件ppt，文件包含高教版2021中职数学基础模块下册95柱锥球及简单组合体1课件PPTppt、高教版2021中职数学基础模块下册95柱锥球及简单组合体1教案doc、高教版2021中职数学基础模块下册教学大纲定稿pdf等3份课件配套教学资源，其中PPT共34页， 欢迎下载使用。

9．5　柱、锥、球及简单组合体
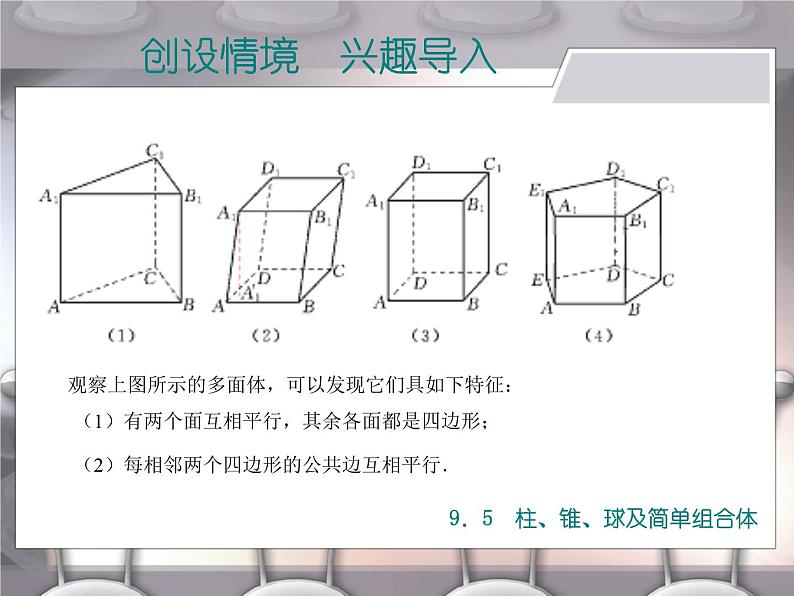
观察上图所示的多面体，可以发现它们具如下特征：
（1）有两个面互相平行，其余各面都是四边形；
（2）每相邻两个四边形的公共边互相平行．
有两个面互相平行，其余每相邻两个面的交线都互相平行的多面体
叫做棱柱,互相平行的两个面，叫做棱柱的底面，其余各面叫做棱柱的
侧面．相邻两个侧面的公共边叫做棱柱的侧棱．两个底面间的距离，
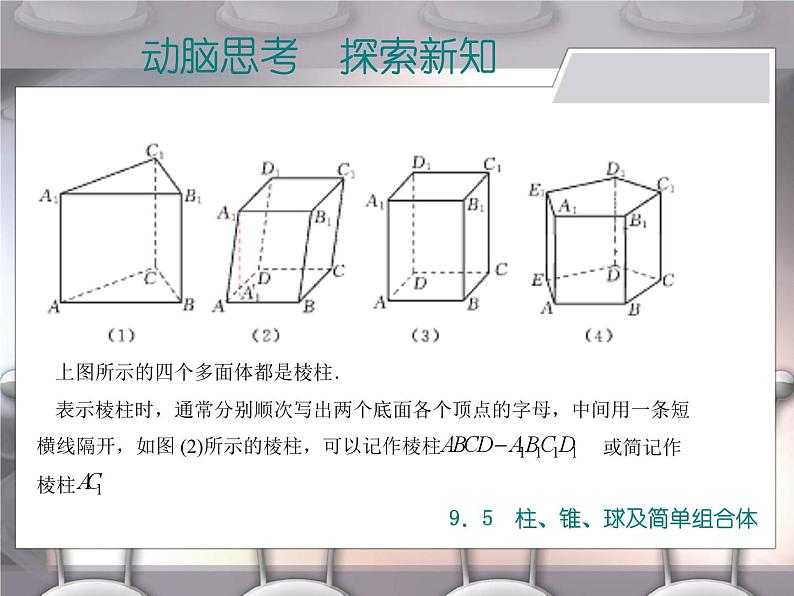
上图所示的四个多面体都是棱柱．
表示棱柱时，通常分别顺次写出两个底面各个顶点的字母，中间用一条短
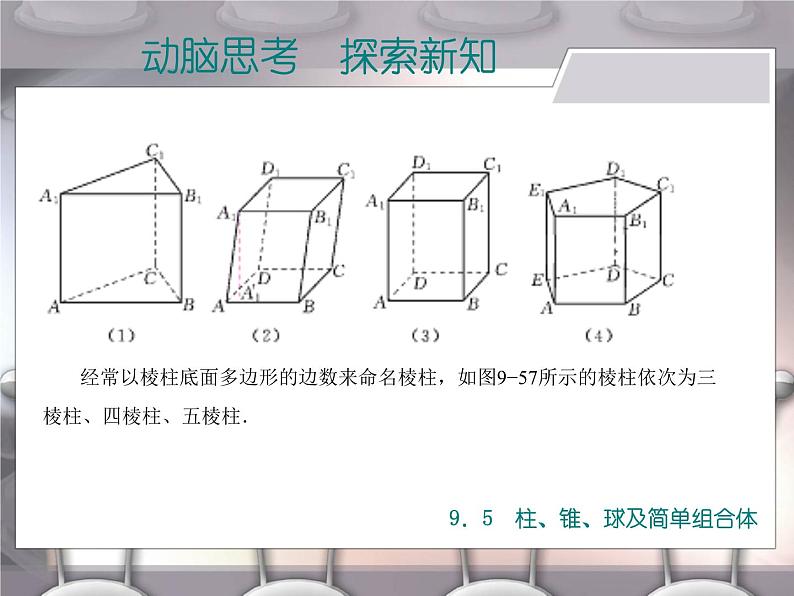
经常以棱柱底面多边形的边数来命名棱柱，如图9−57所示的棱柱依次为三
棱柱、四棱柱、五棱柱．
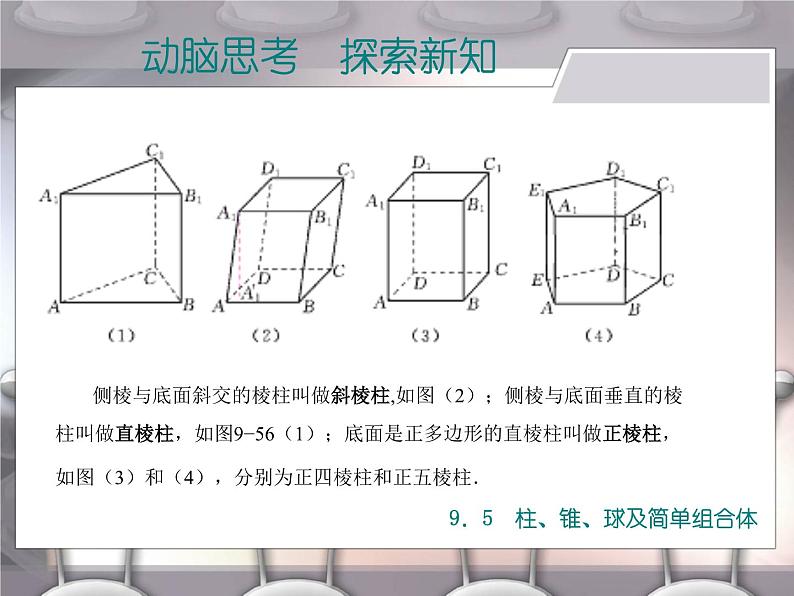
侧棱与底面斜交的棱柱叫做斜棱柱,如图（2）；侧棱与底面垂直的棱
柱叫做直棱柱，如图9−56（1）；底面是正多边形的直棱柱叫做正棱柱，
如图（3）和（4），分别为正四棱柱和正五棱柱．
（1）侧棱垂直于底面，各侧棱长都相等，并且等于正棱柱的高；
（2）两个底面中心的连线是正棱柱的高．
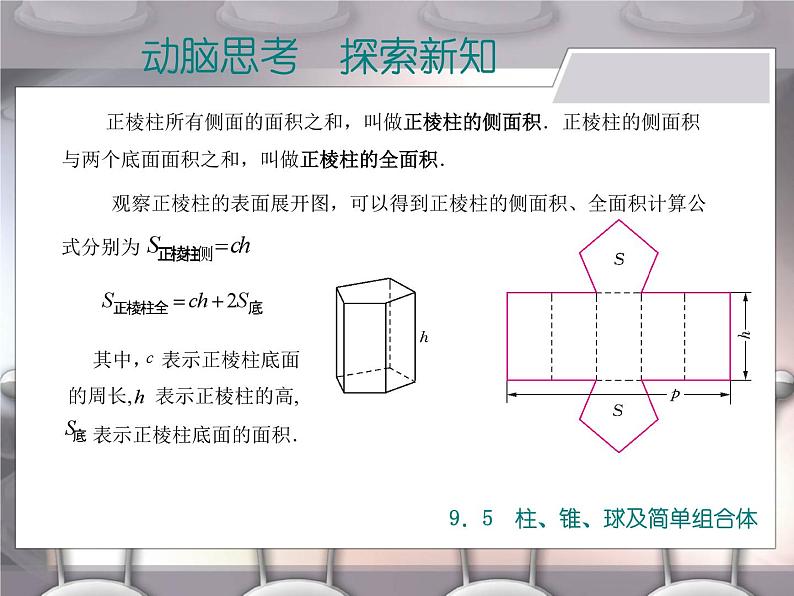
正棱柱所有侧面的面积之和，叫做正棱柱的侧面积．正棱柱的侧面积
与两个底面面积之和，叫做正棱柱的全面积．
观察正棱柱的表面展开图，可以得到正棱柱的侧面积、全面积计算公
正棱柱的体积计算公式为
例 1　已知一个正三棱柱的底面边长为4 cm，高为5 cm，求这个正三
棱柱的侧面积和体积．
解 正三棱锥的侧面积为
利用几何画板可以方便地作出棱柱的直观图形．方法是：首先选中所以绘制棱柱的名称（左图），然后选择合适的位置，点击并拖动，即可得到棱柱的直观图形（右图），最后再标注字母．
观察如图所示的多面体，可以发现它们具如下特征：有一个面是多边形，
其余各面都是三角形，并且这些三角形有一个公共顶点．
底面是正多边形，其余各面是全等的等腰三角形矩形的棱锥叫做正棱锥．图中（1）、（2）分别表示正三棱锥、正四棱锥．
（1）各侧棱的长相等；
（2）各侧面都是全等的等腰三角形．各等腰三角形底边上的高都叫做正
（3）顶点到底面中心的连线垂直与底面，是正棱锥的高；
（4）正棱锥的高、斜高与斜高在底面的射影组成一个直角三角形；
（5）正棱锥的高、侧棱与侧棱在底面的射影也组成一个直角三角形．
观察正棱锥的表面展开图，可以得到正棱锥的侧面积、全面积（表面
准备好同底等高的正三棱锥与正三棱柱形容器，将正三棱锥容器中装满沙
子，然后倒入正三棱柱形状的容器中，发现：连续倒三次正好将正三棱柱容
实验表明，对于同底等高的棱锥与棱柱，棱锥的体积是棱柱体积
例 2　如图，正三棱锥P-ABC中，点O是底面中心，
PO＝12 cm，斜高PD＝13 cm．求它的侧面积、体积
解　在正三棱锥P-ABC中，高PO＝12 cm，斜高PD＝13 cm．
在直角三角形PBD中，
1. 设正三棱柱的高为6，底面边长为4，求它的侧面积、全面积及体积.
2. 正四棱锥的高是a，底面的边长是2a，求它的全面积与体积.
设正三棱柱的高为6，底面边长为4，求它的侧面积、全面积及体积．