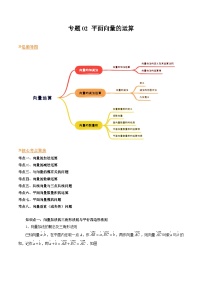
【寒假作业】高中数学 高一寒假巩固提升训练 专题09+简单几何体的表面积与体积(七大考点)-练习
展开思维导图
核心考点聚焦
考点一:棱柱、棱锥、棱台的表面积
考点二:棱柱、棱锥、棱台的体积
考点三:圆柱、圆锥、圆台的表面积
考点四:圆柱、圆锥、圆台的体积
考点五:球的表面积与体积(外接球)
考点六:球的表面积与体积(内切球)
考点七:球的表面积与体积(棱切球)
知识点一、棱柱、棱锥、棱台的表面积
棱柱、棱锥、棱台是多面体,它们的各个面均是平面多边形,它们的表面积就是各个面的面积之和.计算时要分清面的形状,准确算出每个面的面积再求和.棱柱、棱锥、棱台底面与侧面的形状如下表:
知识点诠释:
求多面体的表面积时,只需将它们沿着若干条棱剪开后展开成平面图形,利用平面图形求多面体的表面积.
知识点二、圆柱、圆锥、圆台的表面积
圆柱、圆锥、圆台是旋转体,它们的底面是圆面,易求面积,而它们的侧面是曲面,应把它们的侧面展开为平面图形,再去求其面积.
1、圆柱的表面积
(1)圆柱的侧面积:圆柱的侧面展开图是一个矩形,如下图,圆柱的底面半径为r,母线长,那么这个矩形的长等于圆柱底面周长C=2πr,宽等于圆柱侧面的母线长(也是高),由此可得S圆柱侧=C=2πr.
(2)圆柱的表面积:.
2、圆锥的表面积
(1)圆锥的侧面积:如下图(1)所示,圆锥的侧面展开图是一个扇形,如果圆锥的底面半径为r,母线长为,那么这个扇形的弧长等于圆锥底面周长C=πr,半径等于圆锥侧面的母线长为,由此可得它的侧面积是.
(2)圆锥的表面积:S圆锥表.
3、圆台的表面积
(1)圆台的侧面积:如上图(2)所示,圆台的侧面展开图是一个扇环.如果圆台的上、下底面半径分别为r'、r,母线长为,那么这个扇形的面积为,即圆台的侧面积为S圆台侧=.
(2)圆台的表面积:.
知识点诠释:
求旋转体的表面积时,可从旋转体的生成过程及其几何特征入手,将其展开后求表面积,但要搞清它们的底面半径、母线长与对应的侧面展开图中的边长之间的关系.
知识点三、柱体、锥体、台体的体积
1、柱体的体积公式
棱柱的体积:棱柱的体积等于它的底面积S和高h的乘积,即V棱柱=Sh.
圆柱的体积:底面半径是r,高是h的圆柱的体积是V圆柱=Sh=πr2h.
综上,柱体的体积公式为V=Sh.
2、锥体的体积公式
棱锥的体积:如果任意棱锥的底面积是S,高是h,那么它的体积.
圆锥的体积:如果圆锥的底面积是S,高是h,那么它的体积;如果底面积半径是r,用πr2表示S,则.
综上,锥体的体积公式为.
3、台体的体积公式
棱台的体积:如果棱台的上、下底面的面积分别为S'、S,高是h,那么它的体积是.
圆台的体积:如果圆台的上、下底面半径分别是r'、r,高是h,那么它的体积是
.
综上,台体的体积公式为.
知识点四、球的表面积和体积
1、球的表面积
(1)球面不能展开成平面,要用其他方法求它的面积.
(2)球的表面积
设球的半径为R,则球的表面积公式S球=4πR2.
即球面面积等于它的大圆面积的四倍.
2、球的体积
设球的半径为R,它的体积只与半径R有关,是以R为自变量的函数.
球的体积公式为.
1、正方体的内切球
球与正方体的六个面都相切,称球为正方体的内切球,此时球的半径为r1=a2,过在一个平面上的四个切点作截面如图(1).
2、球与正方体的各条棱相切
球与正方体的各条棱相切于各棱的中点,过球心作正方体的对角面有r2=2a2,如图(2).
3、长方体的外接球
长方体的八个顶点都在球面上,称球为长方体的外接球,根据球的定义可知,长方体的体对角线是球的直径,若长方体过同一顶点的三条棱长为a,b,c,则过球心作长方体的对角面有球的半径为r3=a2+b2+c22,如图(3).
4、正方体的外接球
正方体棱长a与外接球半径R的关系为2R=eq \r(3)a.
5、正四面体的外接球
正四面体的棱长a与外接球半径R的关系为:2R=eq \f(\r(6),2)a.
6、有关球的截面问题
常画出过球心的截面圆,将问题转化为平面中圆的有关问题解决.
考点剖析
考点一:棱柱、棱锥、棱台的表面积
例1.(2024·高一课时练习)如图,已知正三棱柱ABC-A1B1C1的底面边长是2,D,E是CC1,BC的中点,AE=DE.求:
(1)正三棱柱ABC-A1B1C1的侧棱长;
(2)正三棱柱ABC-A1B1C1的表面积.
例2.(2024·全国·高一课堂例题)如图,正四棱锥的底面边长为4,顶点S到底面中心O的距离为4,求它的表面积.
例3.(2024·全国·高一随堂练习)正六棱锥被过棱锥高的中点且平行于底的平面所截,得到正六棱台和较小的棱锥.
(1)求大棱锥、小棱锥、棱台的侧面积之比;
(2)若大棱锥的侧棱长为,小棱锥的底面边长为,求截得的棱台的侧面积与全面积.
变式1.(2024·高一课时练习)如图所示,正六棱锥被过棱锥高PO的中点且平行于底面的平面所截,得到正六棱台和较小的棱锥.
(1)求大棱锥,小棱锥,棱台的侧面面积之比;
(2)若大棱锥PO的侧棱长为12cm,小棱锥的底面边长为4cm,求截得的棱台的侧面面积和表面积.
考点二:棱柱、棱锥、棱台的体积
例4.(2024·高一课时练习)已知正六棱柱最长的对角线长为13cm,其一个侧面的面积为,求棱柱的体积.
例5.(2024·上海虹口·高二校考)已知长方体中,,求:
(1)长方体表面积;
(2)三棱锥的体积.
例6.(2024·福建厦门·高一福建省厦门第二中学校考阶段练习)如图所示,正六棱锥的底面边长为4,H是的中点,O为底面中心,.
(1)求出正六棱锥的高,斜高,侧棱长;
(2)求六棱锥的表面积和体积.
变式2.(2024·陕西榆林·高一校考)已知正四棱台,上底面边长为2,下底面边长为4,高为1.求
(1)该四棱台的侧棱长
(2)该四棱台的体积
变式3.(2024·江西·高二江西师大附中校考阶段练习)如图,在正四棱台中,上底面边长为1,下底面边长为3,侧棱长为2.
(1)求此正四棱台的侧面积;
(2)求此正四棱台的体积.
考点三:圆柱、圆锥、圆台的表面积
例7.(2024·西藏拉萨·统考一模)若一个圆锥的轴截面是一个腰长为,底边上的高为1的等腰三角形,则该圆锥的侧面积为( )
A.B.
C.D.
例8.(2024·福建漳州·高一校联考)已知圆台的上、下底面面积分别为和,高为,则圆台的侧面积为( )
A. B.C.D.
例9.(2024·广东佛山·高一罗定邦中学校联考阶段练习)如图,已知圆锥的底面半径,高,过上一点作平行于底面的截面,以该截面为底面挖去一个圆柱.
(1)若圆柱的底面半径,求剩余部分体积;
(2)试求圆柱侧面积的最大值.
变式4.(2024·安徽·高一安徽师范大学附属中学校考阶段练习)已知一个圆锥的底面半径为2,母线长为4.
(1)求圆锥的侧面展开图的扇形的圆心角;
(2)如图,若圆锥中内接一个高为的圆柱,求该圆柱的侧面积.
变式5.(2024·高一课时练习)如下图,一个圆台形花盆盆口直径为20 cm,盆底直径为15 cm, 底部渗水圆孔直径为1.5 cm,盆壁长为15 cm.为了美化花盆的外观,需要涂油漆.已知每平方米用100毫升油漆,涂100个这样的花盆需要多少毫升油漆?(π取3.14,结果精确到1毫升)
考点四:圆柱、圆锥、圆台的体积
例10.(2024·上海长宁·高二上海市复旦中学校考)如图,高与底面直径相等的圆锥内有一个内接圆柱,当圆柱的侧面积最大时,圆锥与圆柱的体积之比为 .
例11.(2024·广东广州·高一广州市第六十五中学校考阶段练习)圆台的上、下底面半径分别是,,且圆台的母线长为5,则该圆台的体积是 .
例12.(2024·高一课时练习)圆锥的高扩大到原来的倍,底面半径缩短到原来的,则圆锥变化后的体积与原体积的比值为 .
变式6.(2024·上海浦东新·高二校考期末)圆台的轴截面上、下底边长分别为和,母线长为,则圆台的体积是 .
考点五:球的表面积与体积(外接球)
例13.(2024·陕西榆林·高二统考期末)如图,在长方体中,四边形是边长为1的正方形,,则该长方体的外接球表面积是( )
A.B.C.D.
例14.(2024·江苏南京·统考二模)直角三角形中,斜边长为2,绕直角边所在直线旋转一周形成一个几何体.若该几何体外接球表面积为,则长为( )
A.B.1C.D.
例15.(2024·广东·统考一模)如图,在直三棱柱的侧面展开图中,,是线段的三等分点,且.若该三棱柱的外接球的表面积为,则( )
A.B.C.D.
变式7.(2024·江苏南京·高三校联考阶段练习)已知直三棱柱的顶点都在球上,且,,,则此直三棱柱的外接球的表面积是( )
A.B.C.D.
变式8.(2024·安徽阜阳·高二校考阶段练习)某正方体的外接球体积,则此正方体的棱长为( )
A.6B.3C.D.
考点六:球的表面积与体积(内切球)
例16.(2024·湖南·高一校联考期末)已知圆锥的底面半径为,其侧面展开图为一个半圆,则该圆锥的内切球(球与圆锥的底面和侧面均相切)的表面积为 .
例17.(2024·高一单元测试)一个正四面体表面积为,其内切球表面积为S2.则= .
例18.(2024·四川南充·高二四川省阆中东风中学校校考阶段练习)如图所示是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等,相传这个图形表达了阿基米德最引以为自豪的发现.我们来重温这个伟大发现,圆柱的表面积与球的表面积之比为( )
A.B.C.D.
变式9.(2024·广东肇庆·高一校考阶段练习)棱长为2的正方体的内切球的球心为,则球的体积为( )
A.B.C.D.
变式10.(2024·山西太原·高一校考阶段练习)已知正方体的内切球(球与正方体的六个面都相切)的体积是,则该正方体的体积为( )
A.4B.16C.8D.64
考点七:球的表面积与体积(棱切球)
例19.(2024·江西宜春·高三奉新县第一中学校考阶段练习)已知正方体的棱长为2,则与正方体的各棱都相切的球的表面积是 .
例20.(2024·山西朔州·高一校考阶段练习)正四面体的内切球、棱切球(与各条棱均相切的球)及外接球的半径之比为 .
例21.(2024·云南·高三云南师大附中校考阶段练习)在棱长为的正方体中,与其各棱都相切的球的表面积是( )
A.B.C.D.
过关检测
一、单选题
1.(2024·四川南充·统考模拟预测)已知一个圆锥的表面积为,其侧面展开图是一个圆心角为的扇形,则该圆锥的体积为( )
A.B.C.D.
2.(2024·陕西咸阳·高三陕西咸阳中学校考阶段练习)如图是一个实心金属几何体的直观图,它的中间部分是高为的圆柱,上、下两端均是半径为2的半球,若将该实心金属几何体在熔炉中高温熔化(不考虑过程中的原料损失),熔成一个实心球,则该球的直径为( )
A.B.C.D.
3.(2024·全国·模拟预测)已知正三棱台的上、下底面边长分别为4和6,斜高为1,则该正三棱台的体积为( )
A.B.C.D.
4.(2024·安徽·高三校联考阶段练习)已知圆台的上、下底面的半径分别为1,3,其表面积为,则该圆台的体积为( )
A.B.C.D.
5.(2024·黑龙江·校联考模拟预测)若正四棱柱与以正方形的外接圆为底面的圆柱的体积相同,则正四棱柱与该圆柱的侧面积之比为( )
A.B.C.D.
6.(2024·新疆阿克苏·高一校考阶段练习)已知棱长为2的正方体的体积与球的体积相等,则球的半径为( )
A.B.C.D.
7.(2024·全国·模拟预测)某几何体为棱柱或棱锥,且每个面均为边长是2的正三角形或正方形,给出下面4个值:①;②24;③;④.则该几何体的表面积可能是其中的( )
A.①②③B.①③④C.①②④D.①②③④
8.(2024·全国·高一随堂练习)如图,已知正六棱柱的最大对角面的面积为,互相平行的两个侧面的距离为2m,则这个六棱柱的体积为( )
A.B.C.D.以上都不对
二、多选题
9.(2024·全国·模拟预测)已知圆锥的底面圆的半径与球的半径相等,且圆锥,与球的表面积相等,则( )
A.圆锥的母线与底面所成角的余弦值为
B.圆锥的高与母线长之比为
C.圆锥的侧面积与底面积之比为3
D.球的体积与圆锥的体积之比为
10.(2024·广东惠州·高三统考阶段练习)某班级到一工厂参加社会实践劳动,加工出如图所示的圆台,在轴截面中,,且,则( )
A.该圆台的高为1cmB.该圆台轴截面面积为
C.该圆台的侧面积为D.该圆台的体积为
11.(2024·辽宁大连·高一辽师大附中校考阶段练习)一个圆柱和一个圆锥的底面直径和它们的高都与一个球的直径2R相等,下列结论正确的是( )
A.圆柱的侧面积与球的表面积相等
B.圆锥的侧面展开图的圆心角为
C.圆柱的表面积为
D.圆柱的体积等于球与圆锥的体积之和
12.(2024·湖南·高三雅礼中学校联考阶段练习)若某正方体的棱长为,则( )
A.该正方体的体积为5B.该正方体的内切球的体积为
C.该正方体的表面积为30D.该正方体的外接球的表面积为
三、填空题
13.(2024·江西·高一统考)已知正三棱锥的内切球半径为l,若底面边长为,则该棱锥体积为 .
14.(2024·广东·高三执信中学校联考)“升”是我国古代测量粮食的一种容器,在“升”装满后用手指成筷子沿升口刮平,这叫“平升”,如图所示的“升”,从内部测量,其上、下底面均为正方形,边长分别为和,侧面是全等的等腰梯形,梯形的高为,那么这个“升”的“平升”可以装 mL的粮食.(结果保留整数)
15.(2024·河南郑州·高一郑州中学校考期末)已知圆锥的表面积为,它的侧面展开图是一个半圆,则此圆锥的体积为 .
16.(2024·江西南昌·高三江西师大附中校考)已知三棱锥的四个顶点都在球的球面上,且,,,则球的表面积是 .
四、解答题
17.(2024·新疆阿克苏·高一校考阶段练习)正四棱锥的底面边长为4,高为1,求:
(1)求棱锥的体积和侧棱长;
(2)求棱锥的表面积.
18.(2024·上海浦东新·高二上海市洋泾中学校考)某种“笼具”由内、外两层组成,无下底面,内层和外层分别是一个圆锥和一个圆柱,其中圆柱与圆锥的底面周长相等,圆柱有上底面,已知圆柱的底面周长为,高为,圆锥的母线长为.
(1)求这种“笼具”的体积(结果精确到);
(2)现要使用一种纱网材料制作50个“笼具”,该材料的造价为每平方米8元,共需多少元?(结果精确到1元)
19.(2024·河北石家庄·高一校考)如图,在棱长为1的正方体中,、分别是棱、的中点.
(1)求四边形的周长;
(2)求多面体的体积.
20.(2024·内蒙古呼和浩特·高二呼市二中校考)如图,一个几何体是由一个正三棱柱内挖去一个倒圆锥组成,该三棱柱的底面正三角形的边长为2,高为4.圆锥的底面内切于该三棱柱的上底面,顶点在三棱柱下底面的中心处.
(1)求该几何体的体积;
(2)求该几何体的表面积.
项目
名称
底面
侧面
棱柱
平面多边形
平行四边形
面积=底·高
棱锥
平面多边形
三角形
面积=·底·高
棱台
平面多边形
梯形
面积=·(上底+下底)·高
【寒假作业】苏教版2019 高中数学 高二寒假巩固提升训练 复习专题09+数列求和6种常见考法归类-练习.zip: 这是一份【寒假作业】苏教版2019 高中数学 高二寒假巩固提升训练 复习专题09+数列求和6种常见考法归类-练习.zip,文件包含寒假作业苏教版2019高中数学高二寒假巩固提升训练专题09数列求和6种常见考法归类原卷版docx、寒假作业苏教版2019高中数学高二寒假巩固提升训练专题09数列求和6种常见考法归类解析版docx等2份试卷配套教学资源,其中试卷共93页, 欢迎下载使用。
【寒假作业】沪教版2020 高中数学 高二寒假巩固提升训练 专题09+双曲线(四大核心考点六种题型)-练习.zip: 这是一份【寒假作业】沪教版2020 高中数学 高二寒假巩固提升训练 专题09+双曲线(四大核心考点六种题型)-练习.zip,文件包含寒假作业沪教版2020高中数学高二寒假巩固提升训练专题09双曲线四大核心考点六种题型原卷版docx、寒假作业沪教版2020高中数学高二寒假巩固提升训练专题09双曲线四大核心考点六种题型解析版docx等2份试卷配套教学资源,其中试卷共39页, 欢迎下载使用。
【寒假作业】高中数学 高一寒假巩固提升训练 专题07+基本立体图形+(四大考点)-练习: 这是一份【寒假作业】高中数学 高一寒假巩固提升训练 专题07+基本立体图形+(四大考点)-练习,文件包含寒假作业高中数学高一寒假巩固提升训练专题07基本立体图形四大考点原卷版docx、寒假作业高中数学高一寒假巩固提升训练专题07基本立体图形四大考点解析版docx等2份试卷配套教学资源,其中试卷共38页, 欢迎下载使用。