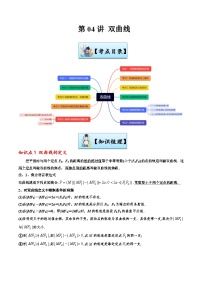
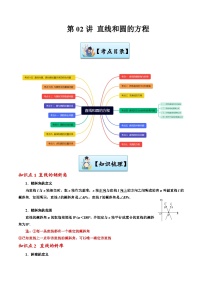
第03讲 椭圆-【寒假讲义】高二数学寒假讲义练习（新人教A专用）

这是一份第03讲 椭圆-【寒假讲义】高二数学寒假讲义练习（新人教A专用），文件包含第03讲椭圆-寒假衔接讲义高二数学寒假讲义练习新人教A专用教师卷docx、第03讲椭圆-寒假衔接讲义高二数学寒假讲义练习新人教A专用学生卷docx等2份试卷配套教学资源，其中试卷共99页， 欢迎下载使用。


【知识梳理】
知识点1 椭圆的定义
平面内与两个定点F1，F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆．这两个定点叫做椭圆的焦点，两焦点间的距离叫做椭圆的焦距．
注：在椭圆的定义中必须要注意以下两个问题
(1)定义中到两定点的距离之和是常数，而不能是变量．
(2)常数(2a)必须大于两定点间的距离，否则轨迹不是椭圆．
①若，M的轨迹为线段；
②若，M的轨迹无图形
知识点2 椭圆的标准方程及简单几何性质
注：1、椭圆的标准方程的特征
①几何特征：椭圆的中心在坐标原点，焦点在x轴或y轴上．
②代数特征：方程右边为1，左边是关于eq \f(x,a)与eq \f(y,b)eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(y,a)与\f(x,b)))的平方和，并且分母为不相等的正值．
③给出椭圆方程(，,),判断该方程所表示的椭圆的焦点位置的方法是:椭圆的焦点在轴上⇔标准方程中项的分母较大;椭圆的焦点在轴上⇔标准方程中项的分母较大,这是判断椭圆焦点所在坐标轴的重要方法.可简记作:焦点位置看大小,焦点跟着大的跑.（x2项和y2项谁的分母大，焦点就在谁的轴上．）
2、椭圆的简单几何性质
(1)椭圆的焦点一定在它的长轴上．
(2)椭圆上到中心的距离最小的点是短轴的两个端点，到中心的距离最大的点是长轴的两个端点．
(3)椭圆上到焦点的距离最大和最小的点分别是长轴的两个端点，最大值为a＋c，最小值为a－c.
(4)椭圆有四个顶点、两个焦点，共六个特殊点，研究椭圆时一定要注意这六个特殊点的位置．
(5)已知椭圆的四个顶点，可以使用几何作图找出其焦点，方法是：以短轴的端点为圆心，a为半径作弧交长轴于两点，这两点就是该椭圆的焦点．
(6)椭圆的离心率e的大小反映椭圆的扁平程度，e越大，椭圆越扁；e越小，椭圆越圆．
拓展：用离心率e＝eq \f(c,a)来刻画椭圆的扁平程度．
如图所示，在Rt△BF2O中，cs∠BF2O＝eq \f(c,a)，记e＝eq \f(c,a)，则0(7)常用椭圆方程的设法
①与椭圆共焦点的椭圆方程可设为：
②有相同离心率：（，焦点在轴上）或（，焦点在轴上）
知识点3 椭圆的焦点三角形
椭圆上的一点与两焦点所构成的三角形称为焦点三角形．解决焦点三角形问题常利用椭圆的定义和正弦定理、余弦定理．
以椭圆eq \f(x2,a2)＋eq \f(y2,b2)＝1(a>b>0)上一点P(x0，y0)(y0≠0)和焦点F1(－c,0)，F2(c,0)为顶点的△PF1F2中，若∠F1PF2＝θ，则
(1)椭圆的定义：|PF1|＋|PF2|＝2a.
(2)余弦定理：4c2＝|PF1|2＋|PF2|2－2|PF1||PF2|·cs θ.
(3)面积公式：S△PF1F2＝eq \f(1,2)|PF1||PF2|·sin θ，当|y0|＝b，即P为短轴端点时，S△PF1F2取最大值，为bc.
重要结论：S△PF1F2=
推导过程：由余弦定理得|F1F2|2=|PF1|2＋|PF2|2－2|PF1||PF2|·cs θ得
由三角形的面积公式可得
S△PF1F2=
=
注：S△PF1F2===（是三角形内切圆的半径）
(4)焦点三角形的周长为2(a＋c)．
(5)在椭圆C：eq \f(x2,a2)＋eq \f(y2,b2)＝1(a>b>0)中,F1，F2是椭圆的两个焦点，P是椭圆上任意的一点，当点P在短轴端点时，最大.
知识点4 点与椭圆的位置关系
点P(x0，y0)与椭圆eq \f(x2,a2)＋eq \f(y2,b2)＝1(a>b>0)的位置关系：
点P在椭圆上⇔eq \f(x\\al(2,0),a2)＋eq \f(y\\al(2,0),b2)＝1；点P在椭圆内部⇔eq \f(x\\al(2,0),a2)＋eq \f(y\\al(2,0),b2)<1；点P在椭圆外部⇔eq \f(x\\al(2,0),a2)＋eq \f(y\\al(2,0),b2)>1.
知识点5 直线与椭圆的位置关系
直线y＝kx＋m与椭圆eq \f(x2,a2)＋eq \f(y2,b2)＝1(a>b>0)的位置关系，判断方法：
联立eq \b\lc\{\rc\ (\a\vs4\al\c1(y＝kx＋m，,\f(x2,a2)＋\f(y2,b2)＝1，))消y得一元二次方程．
当Δ>0时，方程有两解，直线与椭圆相交；
当Δ＝0时，方程有一解，直线与椭圆相切；
当Δ<0时，方程无解，直线与椭圆相离．
知识点6 直线与椭圆相交的弦长公式
1．定义：连接椭圆上两个点的线段称为椭圆的弦．
2．求弦长的方法
(1)交点法：将直线的方程与椭圆的方程联立，求出两交点的坐标，然后运用两点间的距离公式来求．
(2)根与系数的关系法：
如果直线的斜率为k，被椭圆截得弦AB两端点坐标分别为(x1，y1)，(x2，y2)，则弦长公式为：
|AB|＝eq \r(1＋k2)·eq \r(x1＋x22－4x1x2)＝ eq \r(1＋\f(1,k2))·eq \r(y1＋y22－4y1y2).
知识点7 与中点弦有关的问题
1．已知弦是椭圆（）的一条弦，中点坐标为，则的斜率为，运用点差法求的斜率，设，；、都在椭圆上，
两式相减得：，
即 ，故
2.弦的斜率与弦中心和椭圆中心的连线的斜率之积为定值：
【考点剖析】
考点一 求椭圆的标准方程
1．【多选】（2023春·黑龙江哈尔滨·高二哈尔滨德强学校校考阶段练习）若椭圆的一个焦点坐标为，则下列结论中正确的是（ ）
A．B．的长轴长为C．的短轴长为D．的离心率为
2．（2023春·吉林·高二统考期中）过点且与椭圆有相同焦点的椭圆方程为（ ）
A．B．
C．D．
3．（2023春·山西晋城·高二晋城市第二中学校校考阶段练习）已知直线经过焦点在坐标轴上的椭圆的两个顶点，则该椭圆的方程为（ ）
A．B．
C．D．
4．（2023春·上海浦东新·高二上海市建平中学校考阶段练习）椭圆的一个焦点坐标为，且短轴长是长轴长的，则椭圆的标准方程是____．
5．（2023春·天津·高二天津市宁河区芦台第一中学校联考期中）已知，是椭圆的焦点，过且垂直于轴的直线交椭圆于，两点，且，则椭圆的方程为（ ）
A．B．
C．D．
6．（2023·全国·高二假期作业）已知椭圆C：（）的长轴为4，直线与椭圆C相交于A、B两点，若线段的中点为，则椭圆C的方程为（ ）
A．B．C．D．
7．（2023春·重庆万州·高二重庆市万州第二高级中学校考阶段练习）已知椭圆的左､右焦点分别为，过坐标原点的直线交E于P，Q两点，且，且，则E的标准方程为（ ）
A．B．C．D．
考点二 点与椭圆的位置关系
8．（2023·全国·高二假期作业）已知椭圆，则下列各点不在椭圆内部的是（ ）
A．B．
C．D．
9．（2023秋·四川内江·高二四川省资中县第二中学校考阶段练习）点在椭圆的外部，则a的取值范围是（ ）
A．B．
C．D．
10．（2023春·黑龙江绥化·高二校考期末）若直线与：没有交点，则过点的直线与椭圆的交点个数是（ ）
A．至多为B．C．D．
考点三 椭圆的定义及其应用
（一）根据椭圆的方程求参数的范围
11．【多选】（2023春·湖南怀化·高二校考期中）已知方程表示的曲线为，则下列四个结论中正确的是（ ）
A．当或时，曲线是双曲线
B．当时，曲线是椭圆
C．若曲线是焦点在轴上的椭圆，则
D．若曲线是焦点在轴上的椭圆，则
12．（2023春·辽宁大连·高二大连市第二十三中学校联考期中）若方程表示焦点在轴上的椭圆，则实数的取值范围是______．
13．（2023春·河南信阳·高二统考期中）若方程表示焦点在轴上的椭圆，则（ ）
A．，B．，
C．，D．，
14．【多选】（2023春·山东德州·高二统考期中）已知曲线C的方程为（且），则（ ）
A．若曲线C表示圆，则
B．若曲线C表示焦点在x轴上的椭圆，则m的取值范围为
C．若曲线C表示焦点在轴上的椭圆，则m的取值范围为
D．若曲线C表示焦点在轴上的双曲线，则m的取值范围为
椭圆的焦点三角形问题
15．（2023春·陕西西安·高二校考阶段练习）已知椭圆上一点到椭圆一个焦点的距离是7，则点到另一个焦点的距离为（ ）
A．5B．3C．2D．7
16．（2023春·广东深圳·高二校考阶段练习）椭圆的左、右焦点分别为、，过右焦点作直线交椭圆C于A、B两点，若，则__________．
17．（2023春·北京·高二北京市师达中学校考阶段练习）椭圆的两个焦点为，且是椭圆上的一点，则三角形的周长是（ ）
A．1B．C．D．
18．（2023春·福建福州·高二校考期中）已知F是椭圆C：的左焦点，M是椭圆C上任意一点，Q是圆E：上任意一点，则的最小值_________.
19．【多选】（2023春·山东·高二沂水县第一中学校联考期末）已知椭圆C：的左、右焦点分别为，，P为椭圆C上的一个动点，则（ ）
A．
B．
C．内切圆半径的最大值是
D．的最小值是
20．【多选】（2023春·黑龙江哈尔滨·高二哈尔滨市第六中学校校考期中）已知椭圆的左､右焦点分别为，点为椭圆的一个动点，点，则下列结论正确的是（ ）
A．存在点，使得
B．的面积最大值为
C．点到直线距离的最大值为
D．的最大值为7
考点四 求椭圆的离心率
求椭圆的离心率
21．（2023春·吉林长春·高二校考期中）设分别是椭圆的左、右焦点，若椭圆上存在点，使且，则椭圆的离心率为（ ）
A．B．C．D．
22．（2023春·四川资阳·高二四川省安岳中学校考阶段练习）设椭圆 的上顶点为A，左，右焦点分别为，连接并延长交椭圆于点，若，则该椭圆的离心率为________.
23．（2023春·四川乐山·高二校考期中）已知分别是椭圆的左右焦点，是以坐标原点为圆心，以为半径的圆与该椭圆在y轴左侧的两个交点，且是等边三角形，则该椭圆的离心率为（ ）
A．B．C．D．
24．（2023春·辽宁·高二校联考阶段练习）已知椭圆C：的左右焦点分别为，，过点做倾斜角为的直线与椭圆相交于A，B两点，若，则椭圆C的离心率e为（ ）
A．B．C．D．
25．（2023·全国·高二假期作业）已知椭圆上存在两点关于直线对称，且线段中点的纵坐标为，则椭圆的离心率是（ ）
A．B．C．D．
求椭圆的离心率的取值范围
26．（2023春·江西上饶·高二江西省余干中学阶段练习）设､分别是椭圆的左､右焦点，为椭圆上的一点，若的最大值为，则椭圆的离心率的取值范围是_____
27．（2023春·黑龙江哈尔滨·高二哈九中校考阶段练习）已知是椭圆的右焦点，是的上顶点，直线与交于两点.若，到的距离不小于，则的离心率的取值范围是（ ）
A．B．C．D．
28．（2023春·山东枣庄·高二枣庄市第三中学校考期中）已知椭圆是椭圆上的点，是椭圆的左右焦点，若恒成立，则椭圆的离心率的取值范围是__________.
（三）由椭圆的离心率求参数（范围）
29．【多选】（2023春·重庆·高二校联考阶段练习）若椭圆的离心率为，则实数的取值可能是（ ）
A．10B．8C．5D．4
30．（2023·全国·高二假期作业）已知焦点在x轴上的椭圆的离心率为，则k的值为___________.
31．（2023·高二课时练习）已知椭圆的离心率，则实数m的取值范围是_____．
32．（2023春·新疆乌鲁木齐·高二乌鲁木齐市第70中校考期中）椭圆（）的左、右焦点分别是，，斜率为1的直线l过左焦点，交C于A，B两点，且的内切圆的面积是，若椭圆C的离心率的取值范围为，则线段AB的长度的取值范围是（ ）
A．B．C．D．
考点五 与椭圆有关的轨迹问题
33．（2023春·四川成都·高二树德中学校考期中）已知圆，圆，动圆M与圆外切，同时与圆内切，则动圆圆心M的轨迹方程为（ ）
A．B．
C．D．
34．（2023春·山西运城·高二校联考阶段练习）在平面直角坐标系中，已知圆：（圆心为），点，点Р在圆A上运动，设线段PB的垂直平分线和直线PA的交点为Q，则点Q的轨迹方程为（ ）
A．B．
C．D．
35．（2023春·四川成都·高二树德中学校考期中）已知的周长为20，且顶点，则顶点的轨迹方程是（ ）
A．B．C．D．
36．（2023春·湖北省直辖县级单位·高二校考期中）已知点、，动点满足：直线的斜率与直线的斜率之积为，则的取值范围为（ ）
A．B．C．D．
37．（2023春·四川巴中·高二四川省平昌中学校考阶段练习）设满足：，则点的轨迹为（ ）
A．圆B．椭圆C．椭圆或线段D．线段
考点六 直线与椭圆的位置关系
38．（2023春·山东滨州·高二校考期中）已知直线，椭圆，则直线与椭圆的位置关系是（ ）
A．相交B．相切C．相离D．无法确定
39．（2023春·四川成都·高二双流中学校考期中）若直线 与圆没有交点，则过点的直线与椭圆的交点的个数为（ ）
A．0或1B．2C．1D．0或1或2
40．（2023·高二单元测试）定义曲线为椭圆的“倒椭圆”，已知椭圆，它的倒椭圆为，过上任意一点做直线垂直轴于点，作直线垂直轴于点，则直线与椭圆的公共点个数为（ ）
A．0B．1
C．2D．与点的位置关系
41．（2023春·江苏无锡·高二统考期末）椭圆＝1的一个焦点为F，过原点O作直线（不经过焦点F）与椭圆交于A，B两点，若△ABF的面积是20，则直线AB的斜率为（ ）
A．B．C．D．
42．（2023春·河南安阳·高二校联考阶段练习）设椭圆的左焦点为F，上下顶点分别为A、B，直线AF的斜率为，并交椭圆于另一点C，则直线BC的斜率为（ ）
A．B．C．D．
考点七 弦长及中点弦问题
弦长问题
43．（2023·高二课时练习）一条过原点的直线与椭圆的一个交点为，则它被椭圆截得的弦长等于（ ）
A．3B．6C．D．
44．（2023·高二课时练习）直线y＝x+m与椭圆交于A，B两点，若弦长，则实数m的值为（ ）
A．B．±1C．D．±2
45．（2023·全国·高二专题练习）直线与椭圆相交两点，点是椭圆上的动点，则面积的最大值为（ ）
A．2B．C．D．3
46．（2023春·黑龙江哈尔滨·高二哈尔滨德强学校校考期中）已知斜率为1的直线l过椭圆的右焦点，交椭圆于A，B两点，则弦AB的长为（ ）
A．B．C．D．
47．（2023春·内蒙古赤峰·高二赤峰二中校考阶段练习）已知椭圆（）的左、右焦点分别为，，过的直线交椭圆于两点，若的最大值为10，则的值是（ ）
A．B．C．D．
（二）中点弦问题
48．（2023秋·福建厦门·高二厦门双十中学校考阶段练习）已知直线，椭圆．若直线l与椭圆C交于A，B两点，则线段AB的中点的坐标为（ ）
A．B．
C．D．
49．（2023春·内蒙古包头·高二包头一中校考期中）椭圆中，以点为中点的弦所在直线斜率为（ ）
A．1B．C．－1D．
50．（2023春·四川眉山·高二眉山中学校考期中）已知焦点在轴上的椭圆的一条弦所在的直线方程是，弦的中点坐标是，则椭圆的短轴长为（ ）
A．2B．4C．8D．16
51．（2023春·河南许昌·高二校考期中）已知过椭圆左焦点F且与长轴垂直的弦长为，过点且斜率为-1的直线与相交于两点，若恰好是的中点，则椭圆上一点到的距离的最大值为（ ）
A．6B．C．D．
52．（2023春·湖北襄阳·高二襄阳市第一中学校考阶段练习）已知椭圆（）的一条弦所在的直线方程是，弦的中点坐标是，则椭圆的离心率是（ ）
A．B．C．D．
53．（2023春·安徽芜湖·高二芜湖一中校考期中）已知椭圆的右焦点为，过作直线交椭圆于A、B陃点，若弦中点坐标为，则椭圆的方程为（ ）
A．B．
C．D．
考点八 求椭圆的参数或范围问题
54．（2023·全国·高二假期作业）已知椭圆上存在关于直线对称的点，则实数m的取值范围为（ ）
A．B．C．D．
55．（2023秋·江苏南京·高二南京市中华中学校考开学考试）椭圆C：的左右顶点分别为，点P在C上且直线斜率的取值范围是，那么直线斜率的取值范围是
A．B．C．D．
56．（2023秋·四川成都·高二校联考开学考试）已知椭圆，过定点的直线l与椭圆交于不同的两点A、B，O为坐标原点，若为锐角，则直线l的斜率k的取值范围为（ ）．
A．B．
C．D．
57．（2023春·黑龙江哈尔滨·高二哈师大附中校考阶段练习）已知椭圆：的左、右焦点分别为、，若上存在无数个点，满足：，则的取值范围为（ ）
A． B． C． D．
58．（2023春·四川·高二四川省科学城第一中学校考期中）已知椭圆的短轴长为，焦距为，、分别是椭圆的左、右焦点，若点为上的任意一点，则 的取值范围为（ ）
A．[1，7]B．[1，28]C．D．
考点九 求椭圆的最值问题
59．（2023春·海南·高二校考阶段练习）椭圆上的点到直线：的距离的最小值为（ ）
A．B．C．D．
60．（2023春·浙江杭州·高二杭州四中校考期中）设P是椭圆上的任一点，EF为圆的任一条直径，则的最大值为__________．
61．（2023春·江苏淮安·高二江苏省清江中学校考阶段练习）设椭圆的左､右焦点为､，是椭圆上的动点，则下列结论正确的是（ ）
A．离心率 B．的最大值为3
C．△面积的最大值为D．的最小值为2
62．（2023·高二课时练习）已知椭圆C：上的动点P到右焦点距离的最小值为，则（ ）
A．1B．C．D．
63．（2023秋·四川绵阳·高二四川省绵阳南山中学校考开学考试）已知，，分别是椭圆的左右焦点，点Q是C上一点，延长至点P，连接，若线段的垂直平分线恰过点Q，则面积的最大值为（ ）
A．4B．2C．3D．
考点十 椭圆的定点、定值问题
64．（2023春·江苏泰州·高二统考期中）已知椭圆，点为直线上一动点，过点向椭圆作两条切线、，、为切点，则直线过定点_______．
65．（2023春·湖北恩施·高二校考阶段练习）已知分别是双曲线的左、右焦点，点A是C的左顶点，，C的离心率为2.
(1)求C的方程；
(2)直线l与C交于M，N两点（M，N异于双曲线C的左、右顶点），若以为直径的圆经过点A，求证：直线l恒过定点.
66．（2023春·四川资阳·高二校考期中）已知椭圆 离心率， 过椭圆中心的直线交椭圆于两点 (在第一象限)， 过作轴垂线交椭圆于点， 过作直线垂直交椭圆于点， 连接交于点， 则_______________．
67．（2023春·广东深圳·高二校考阶段练习）已知椭圆上一点P到两个焦点的距离之和为4，离心率为．
(1)求椭圆C的方程；
(2)过点的直线与椭圆交于A、B两点，为左焦点，记直线的斜率为，直线的斜率为，求证：．
68．（2023春·北京海淀·高二校考阶段练习）已知点为椭圆C：上一点，A、B分别为C的左、右顶点，且的面积为5．
(1)求C的标准方程；
(2)过点的直线l与C相交于点M，N（点M在x轴上方），AM，BN与y轴分别交于点G，H，记，分别为，（点O为坐标原点）的面积，证明：为定值．
考点十一 椭圆中的向量问题
69．（2023春·陕西咸阳·高二校考阶段练习）已知椭圆的右焦点为，离心率．
(1)求的方程；
(2)过点的直线与椭圆交于两点，若，求的方程．
70．（2023·全国·高二假期作业）设椭圆的右顶点为A，上顶点为B．已知椭圆的离心率为，．
(1)求椭圆的方程；
(2)设直线l：与椭圆交于P，Q两点，l与直线AB交于点M，且点P，M均在第四象限．若，求k的值．
71．（2023春·四川凉山·高二校考阶段练习）已知为椭圆的左､右焦点，点为椭圆上一点，且
(1)求椭圆的标准方程；
(2)若圆是以为直径的圆，直线与圆相切，并与椭圆交于不同的两点､，且，求的值
72．（2023·高二单元测试）已知椭圆的长轴长为，右焦点到直线的距离为.
(1)求椭圆的方程；
(2)若直线与椭圆交于，两点，椭圆上存在点，使得，求实数的值.
73．（2023春·河南鹤壁·高二河南省浚县第一中学校考阶段练习）已知椭圆的离心率为，短轴一个端点到右焦点的距离为2.
(1)求椭圆的标准方程；
(2)过点的直线交椭圆于两点，交轴于点，设，试判断是否为定值？请说明理由.
考点十二 椭圆的实际应用问题
74．（2023春·湖北·高二华中科技大学附属中学校联考期中）在一些山谷中有一种奇特的现象，在一处呼喊一声，在另一处会间隔听到两次呼喊，前一次是声音直接传到听者耳朵中，后一次是声音经过山壁反射后再传到听者耳朵中.假设有一片椭圆形状的空旷山谷，甲､乙两人分别站在椭圆的两个焦点处，甲呼喊一声，乙经过听到第一声，又过听到第二声，则该椭圆的离心率为（ ）
A．B．C．D．
75．（2023·高二课时练习）2021年2月10日，天问一号探测器顺利进入火星的椭圆环火轨道（将火星近似看成一个球体，球心为椭圆的一个焦点）．2月15日17时，天问一号探测器成功实施捕获轨道远火点（椭圆轨迹上距离火星表面最远的一点）平面机动，同时将近火点高度调整至约265km．若此时远火点距离约为11945km，火星半径约为3395km，则调整后天问一号的运行轨迹（环火轨道曲线）的焦距约为（ ）
A．11680kmB．5840kmC．19000kmD．9500km
76．（2023春·广东广州·高二广州市第九十七中学校考阶段练习）我国发射的第一颗人造地球卫星的运行轨道是以地球的中心（简称“地心”）为一个焦点的椭圆，已知它的近地点（离地面最近的点）距地面，远地点（离地面最远的点）距地面，是椭圆的长轴，地球半径为，则卫星运行的椭圆轨道的长轴的长为______．
考点十三 与椭圆有关的综合问题
77．【多选】（2023春·黑龙江·高二黑龙江实验中学校考期中）已知椭圆的左，右焦点分别为，，椭圆的上顶点和右顶点分别为，，若为椭圆上任意一点，且，关于坐标原点对称，则（ ）
A．
B．椭圆上存在无数个点，使得
C．直线和的斜率之积为
D．面积的最大值为
78．【多选】（2023春·福建·高二福建师大附中校考期末）已知椭圆的左､右两个端点分别为为椭圆上一动点，则下列说法正确的是（ ）
A．的周长为6
B．的最大面积为
C．存在点使得
D．的最大值为7
79．【多选】（2023春·吉林长春·高二校考期中）点分别为椭圆的左、右焦点且．点P为椭圆上任意一点，的面积的最大值是1，点M的坐标为，过点且斜率为k的直线L与椭圆C相交于A，B两点，则下列结论成立的是（ ）
A．椭圆的离心率
B．的值与k相关
C．的值为常数
D．的值为常数-1
【过关检测】
1．（2023秋·贵州遵义·高二统考期末）若直线过椭圆短轴端点和左顶点，则椭圆方程为（ ）
A．B．C．D．
2．（2023春·广东江门·高二统考期末）己知是椭圆的两个焦点，点在上，则的最大值为（ ）
A．36B．25C．20D．16
3．（2023春·河南·高二沈丘县第一高级中学校联考期末）已知椭圆的长轴长是短轴长的倍，左焦点、右顶点和下顶点分别为，坐标原点到直线的距离为，则 的面积为（ ）
A．B．4C．D．
4．（2023春·湖北·高二校联考期末）过椭圆左焦点作倾斜角为的直线，与椭圆交于、两点，其中为线段的中点，线段的长为，则椭圆的离心率为（ ）
A．B．C．D．
5．（2023春·河南郑州·高二统考期末）已知点是椭圆的左右焦点，椭圆上存在不同两点使得，则椭圆的离心率的取值范围是（ ）
A．B．C．D．
6．（2023春·福建福州·高二校联考期末）已知P是椭圆上的一点，是椭圆的两个焦点且，则的面积是（ ）
A．B．2C．D．1
7．【多选】（2023春·广东茂名·高二统考期末）已知曲线，下列说法正确的是（ ）
A．若，，则是两条直线
B．若，则是圆，其半径为
C．若，则是椭圆，其焦点在轴上
D．若，则是双曲线，其渐近线方程为
8．【多选】（2023·全国·高二假期作业）已知椭圆：内一点，直线与椭圆交于A，B两点，且M为线段AB的中点，则下列结论正确的是（ ）
A．椭圆的焦点坐标为、B．椭圆的长轴长为
C．直线的方程为D．
9．【多选】（2023春·江苏南京·高二校联考阶段练习）已知椭圆的左右焦点分别为，直线与椭圆交于两点，分别为椭圆的左右顶点，则下列命题正确的有（ ）
A．若直线的斜率为，直线的斜率，则
B．若有且仅有两个不同的实数使得为等腰直角三角形，则
C．取值范围为
D．周长的最大值为8
10．（2023秋·上海闵行·高二校考期末）若点和点分别为椭圆的中心和左焦点，点为椭圆上的任意一点，则的取值范围为_______．
11．（2023春·江苏苏州·高二苏州中学校考期末）已知椭圆方程为，且椭圆内有一条以点为中点的弦，则弦所在的直线的方程是__________.
12．（2023春·四川成都·高二树德中学校考期中）已知椭圆的左右顶点分别为A，B，点P为椭圆上异于A，B的任意一点．
(1)求直线PA与PB的斜率之积；
(2)任意过且与x轴不重合的直线交椭圆E于M，N两点，证明：以MN为直径的圆恒过点A．
13．（2023春·山东青岛·高二山东省青岛第五十八中学校考期中）已知，是椭圆M：的左右焦点．
(1)若C是椭圆上一点，求的最小值；
(2)直线与椭圆M交于A，B两点，O是坐标原点．椭圆M上存在点P使得四边形OAPB为平行四边形，求m的值．
14．（2023春·四川泸州·高二四川省泸县第一中学校考期末）已知椭圆的左右焦点分别为，抛物线与椭圆有相同的焦点，点P为抛物线与椭圆在第一象限的交点，且．
(1)求椭圆的方程；
(2)过F作两条斜率不为0且互相垂直的直线分别交椭圆于A，B和C，D，线段AB的中点为M，线段CD的中点为N，证明：直线过定点，并求出该定点的坐标．
15．（2023春·广西·高二校联考阶段练习）设动点到定点的距离和它到定直线的距离之比为，记动点的轨迹为曲线．
(1)求的方程；
(2)点，在曲线上且，点满足且，求直线的方程．
焦点的位置
焦点在x轴上
焦点在y轴上
图形
标准方程
eq \f(x2,a2)＋eq \f(y2,b2)＝1(a＞b＞0)
eq \f(y2,a2)＋eq \f(x2,b2)＝1(a＞b＞0)
范围
－a≤x≤a且－b≤y≤b
－b≤x≤b且－a≤y≤a
顶点
A1(－a,0)，A2(a,0),_ B1(0，－b)，B2(0，b)
A1(0，－a)，A2(0，a), B1(－b,0)，B2(b,0)
轴长
长轴长＝eq \a\vs4\al(2a)，短轴长＝eq \a\vs4\al(2b)
焦点
F1(－c,0)，F2(c,0)
F1(0，－c)，F2(0，c)
焦距
|F1F2|＝eq \a\vs4\al(2c)
对称性
对称轴x轴和y轴，对称中心(0,0)
离心率
e＝eq \f(c,a)(0