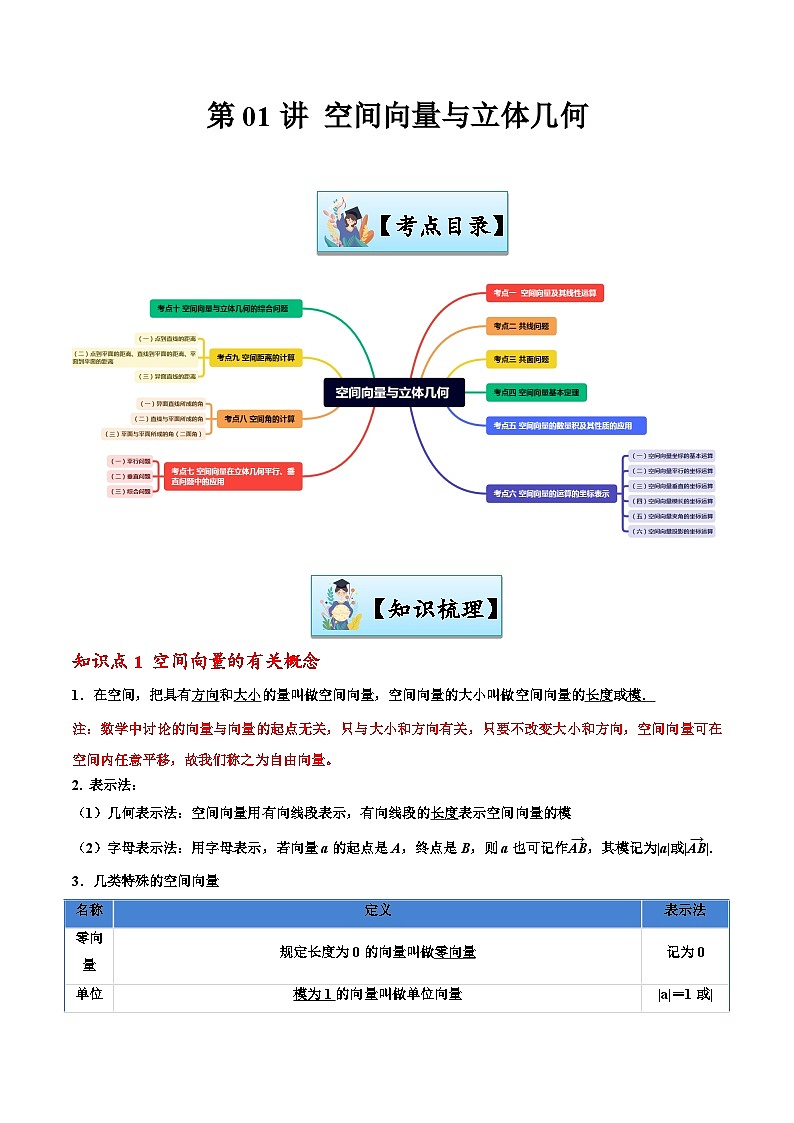
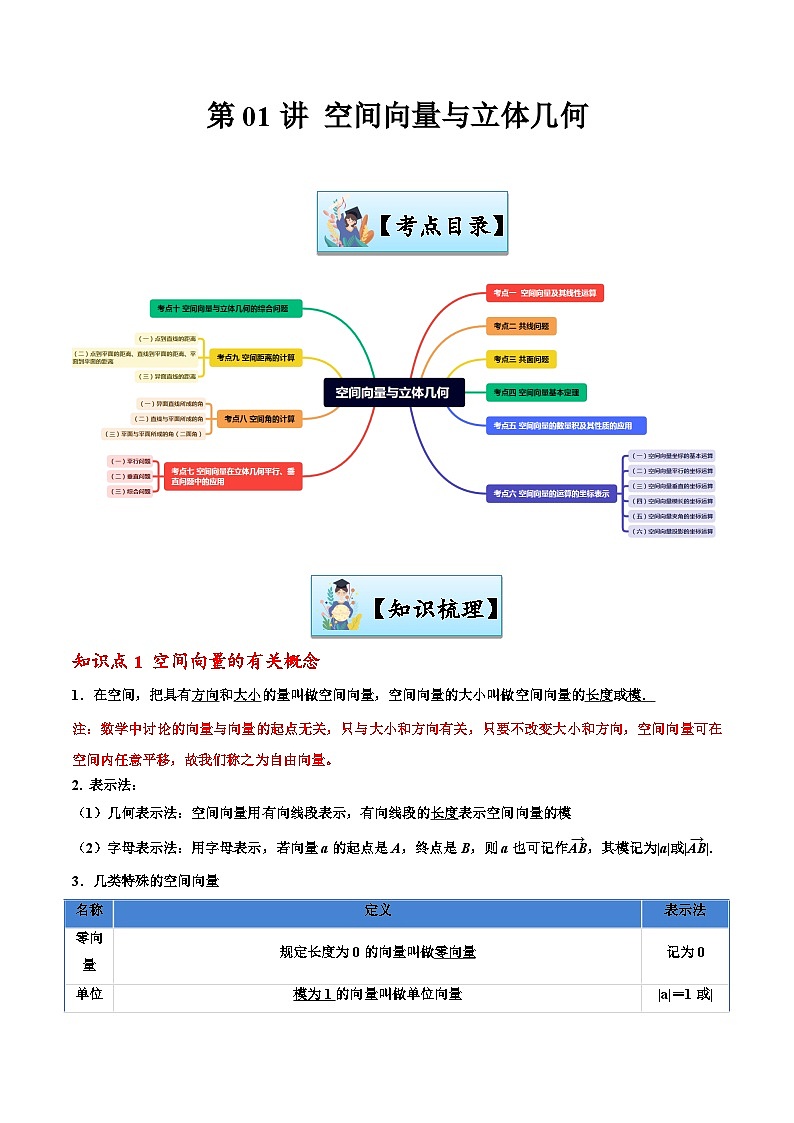
第01讲 空间向量与立体几何-【寒假讲义】高二数学寒假讲义练习（新人教A专用）

这是一份第01讲 空间向量与立体几何-【寒假讲义】高二数学寒假讲义练习（新人教A专用），文件包含第01讲空间向量与立体几何-寒假衔接讲义高二数学寒假讲义练习新人教A专用教师卷docx、第01讲空间向量与立体几何-寒假衔接讲义高二数学寒假讲义练习新人教A专用学生卷docx等2份试卷配套教学资源，其中试卷共131页， 欢迎下载使用。


【考点目录】
【知识梳理】
知识点1 空间向量的有关概念
1．在空间，把具有方向和大小的量叫做空间向量，空间向量的大小叫做空间向量的长度或模．
注：数学中讨论的向量与向量的起点无关，只与大小和方向有关，只要不改变大小和方向，空间向量可在空间内任意平移，故我们称之为自由向量。
2. 表示法：
（1）几何表示法：空间向量用有向线段表示，有向线段的长度表示空间向量的模
（2）字母表示法：用字母表示，若向量a的起点是A，终点是B，则a也可记作eq \(AB,\s\up6(→))，其模记为|a|或|eq \(AB,\s\up6(→))|.
3．几类特殊的空间向量
知识点2 空间向量的线性运算
（一）空间向量的加减运算
（二）空间向量的数乘运算
知识点3 共线向量与共面向量
1．共线向量与共面向量的区别
2.直线l的方向向量
如图O∈l，在直线l上取非零向量a，设P为l上的任意一点，则∃λ∈R使得eq \(OP,\s\up7(―→))＝λa.
定义：把与a平行的非零向量称为直线l的方向向量．
知识点4 空间向量的夹角
知识点5 空间向量的数量积运算
1．(1)空间向量的数量积
已知两个非零向量a，b，则|a||b|cs〈a，b〉叫做a，b的数量积，记作a·b，即a·b＝|a||b|·cs〈a，b〉．零向量与任意向量的数量积为0，即0·a＝0.
注：等于的长度与在的方向上的投影的乘积．
(2)运算律
2.投影向量及直线与平面所成的角
(1)如图①，在空间，向量a向向量b投影，由于它们是自由向量，因此可以先将它们平移到同一个平面α内，进而利用平面上向量的投影，得到与向量b共线的向量c，c＝|a|cs〈a，b〉eq \f(b,|b|)，向量c称为向量a在向量b上的投影向量．类似地，可以将向量a向直线l投影(如图②)．
(2)如图③，向量a向平面β投影，就是分别由向量a的起点A和终点B作平面β的垂线，垂足分别为A′，B′，得到向量eq \(A′B′,\s\up6(——→))，向量eq \(A′B′,\s\up6(——→))称为向量a在平面β上的投影向量．这时，向量a，eq \(A′B′,\s\up6(——→))的夹角就是向量a所在直线与平面β所成的角．
知识点6 空间向量数量积运算律及性质
1、数量乘积的运算律：
； ； ．
2、若，为非零向量，为单位向量，则有
；；
，，；；．
知识点7 空间向量基本定理
1．定理
如果三个向量a，b，c不共面，那么对任意一个空间向量p，存在唯一的有序实数组(x，y，z)，使得p=xa+yb+zc.其中{a，b，c}叫做空间的一个基底，a，b，c都叫做基向量．如果p=xa+yb+zc，则称xa+yb+zc为p在基底{a，b，c}下的分解式.
2．空间向量的正交分解
(1)单位正交基底：空间的一个基底中的三个基向量两两垂直，且长度都为1，常用{i，j，k}表示．
(2)正交分解：由空间向量基本定理可知，对空间中的任意向量a，均可以分解为三个向量xi，yj，zk，使a＝xi＋yj＋zk.像这样，把一个空间向量分解为三个两两垂直的向量，叫做把空间向量正交分解．
知识点8 空间向量基本定理应用
1、证明平行、共面问题
(1)对于空间任意两个向量a，b(b≠0)，a∥b的充要条件是存在实数λ，使a＝λb.
(2) 如果两个向量a，b不共线，那么向量p与向量a，b共面的充要条件是存在唯一的有序实数对(x，y)，使p＝xa＋yb.
(3)直线平行和点共线都可以转化为向量共线问题；点线共面可以转化为向量共面问题．
2、求夹角、证明垂直问题
(1)θ为a，b的夹角，则cs θ＝eq \f(a·b,|a||b|). (2)若a，b是非零向量，则a⊥b⇔a·b＝0.
3、求距离(长度)问题
eq \b\lc\|\rc\|(\a\vs4\al\c1(a))＝eq \r(a·a)( eq \b\lc\|\rc\|(\a\vs4\al\c1(\(AB,\s\up6(→))))＝eq \r(\(AB,\s\up6(→))·\(AB,\s\up6(→))) )．
知识点9 空间直角坐标系
1．空间直角坐标系
(1)空间直角坐标系：在空间选定一点O和一个单位正交基底{i，j，k}，以O为原点，分别以i，j，k的方向为正方向，以它们的长为单位长度建立三条数轴：x轴、y轴、z轴，它们都叫做坐标轴，这时我们就建立了一个空间直角坐标系Oxyz.
(2)相关概念：O叫做原点，i，j，k都叫做坐标向量，通过每两条坐标轴的平面叫做坐标平面，分别称为Oxy平面、Oyz平面、Ozx平面，它们把空间分成八个部分．
注意点：
(1)基向量：|i|＝|j|＝|k|＝1，i·j＝i·k＝j·k＝0.
(2)画空间直角坐标系Oxyz时，一般使∠xOy＝135°(或45°)，∠yOz＝90°.
(3)建立的坐标系均为右手直角坐标系．在空间直角坐标系中，让右手拇指指向x轴的正方向，食指指向y轴的正方向，如果中指指向z轴的正方向，则称这个坐标系为右手直角坐标系．
2．空间一点的坐标、向量的坐标
（1）空间点的坐标
在空间直角坐标系Oxyz中，i，j，k为坐标向量，对空间任意一点A，对应一个向量eq \(OA,\s\up6(→))，且点A的位置由向量eq \(OA,\s\up6(→))唯一确定，由空间向量基本定理，存在唯一的有序实数组(x，y，z)，使eq \(OA,\s\up6(→))＝xi＋yj＋zk.在单位正交基底{i，j，k}下与向量eq \(OA,\s\up6(→))对应的有序实数组(x，y，z)，叫做点A在空间直角坐标系中的坐标，记作A(x，y，z)，其中x叫做点A的横坐标，y叫做点A的纵坐标，z叫做点A的竖坐标．
注：空间直角坐标系中坐标轴、坐标平面上的点的坐标特点
（2）空间点的对称问题
①空间点的对称问题可类比平面直角坐标系中点的对称问题，要掌握对称点的变化规律，才能准确求解．
②对称点的问题常常采用“关于谁对称，谁保持不变，其余坐标相反”这个结论．
（3）空间向量的坐标
向量的坐标：在空间直角坐标系Oxyz中，给定向量a，作eq \(OA,\s\up6(→))＝a，由空间向量基本定理，存在唯一的有序实数组(x，y，z)，使a＝xi＋yj＋zk.有序实数组(x，y，z)叫做a在空间直角坐标系Oxyz中的坐标，可简记作a＝(x，y，z)．
知识点10 空间向量的坐标运算
1．空间向量的坐标运算法则
设向量a＝(a1，a2，a3)，b＝(b1，b2，b3)，λ∈R，那么
注意点：
(1)空间向量运算的坐标表示与平面向量的坐标表示完全一致．
(2)设A(x1，y1，z1)，B(x2，y2，z2)，则eq \(AB,\s\up6(→))＝(x2－x1，y2－y1，z2－z1)．即一个空间向量的坐标等于表示此向量的有向线段的终点坐标减去起点坐标．
(3)运用公式可以简化运算：(a±b)2＝a2±2a·b＋b2；(a＋b)·(a－b)＝a2－b2.
(4)向量线性运算的结果仍是向量，用坐标表示；数量积的结果为数量．
2．空间向量相关结论的坐标表示
设a＝(a1，a2，a3)，b＝(b1，b2，b3)，则有
(1)平行关系：当b≠0时，a∥b⇔a＝λb⇔a1＝λb1，a2＝λb2，a3＝λb3(λ∈R)；
(2)垂直关系：a⊥b⇔a·b＝0⇔a1b1＋a2b2＋a3b3＝0.
(3)|a|＝eq \r(a·a)＝eq \r(a\\al(2,1)＋a\\al(2,2)＋a\\al(2,3)).
(4)cs〈a，b〉＝eq \f(a·b,|a||b|)＝eq \f(a1b1＋a2b2＋a3b3,\r(a\\al(2,1)＋a\\al(2,2)＋a\\al(2,3))·\r(b\\al(2,1)＋b\\al(2,2)＋b\\al(2,3))).
3．空间两点间的距离公式
在空间直角坐标系中，设P1(x1，y1，z1)，P2(x2，y2，z2)．
(1)eq \(P1P2,\s\up7(――→))＝(x2－x1，y2－y1，z2－z1)．
(2)P1P2＝|eq \(P1P2,\s\up7(――→))|＝eq \r((x2－x1)2＋(y2－y1)2＋(z2－z1)2).
(3)若O(0,0,0)，P(x，y，z)，则|eq \(OP,\s\up6(→))|＝eq \r(x2＋y2＋z2).
知识点11 空间中点、直线和平面的向量表示
1．空间直线的向量表示式
设A是直线上一点，a是直线l的方向向量，在直线l上取eq \(AB,\s\up6(→))＝a，设P是直线l上任意一点，
(1)点P在直线l上的充要条件是存在实数t，使eq \(AP,\s\up6(→))＝ta，即eq \(AP,\s\up6(→))＝teq \(AB,\s\up6(→)).
(2)取定空间中的任意一点O，点P在直线l上的充要条件是存在实数t.使eq \(OP,\s\up6(→))＝eq \(OA,\s\up6(→))＋ta.
(3)取定空间中的任意一点O，点P在直线l上的充要条件是存在实数t，使eq \(OP,\s\up6(→))＝eq \(OA,\s\up6(→))＋teq \(AB,\s\up6(→)).
2．空间平面的向量表示式
①如图，设两条直线相交于点O，它们的方向向量分别为a和b，P为平面α内任意一点，由平面向量基本定理可知，存在唯一的有序实数对(x，y)，使得eq \(OP,\s\up6(→))＝xa＋yb.
②如图，取定空间任意一点O，空间一点P位于平面ABC内的充要条件是存在实数x，y，使eq \(OP,\s\up6(→))＝eq \(OA,\s\up6(→))＋xeq \(AB,\s\up6(→))＋yeq \(AC,\s\up6(→)).我们把这个式子称为空间平面ABC的向量表示式．
③由此可知，空间中任意平面由空间一点及两个不共线向量唯一确定．
如图，直线l⊥α，取直线l的方向向量a，我们称向量a为平面α的法向量．给定一个点A和一个向量a，那么过点A，且以向量a为法向量的平面完全确定，可以表示为集合{P|a·eq \(AP,\s\up6(→))＝0}．
知识点12 空间平行、垂直关系的向量表示
知识点13 空间距离及向量求法
知识点14 空间角及向量求法
【考点剖析】
考点一 空间向量及其线性运算
1．（2023·重庆·高二期末）在长方体中，（ ）
A．B．C．D．
【答案】D
【分析】根据向量的运算法则得到，带入化简得到答案.
【详解】在长方体中，易知，
所以.
故选：D.
2．（2023·湖南益阳·高二期末）在四面体中，为的中点，为棱上的点，且，则（ ）
A．B．
C．D．
【答案】A
【分析】利用空间向量加法运算，减法运算，数乘运算即可得到答案.
【详解】如图
故选：A
3．（2023·陕西商洛·高二期末（理））在平行六面体中，点在上，且，若，则（ ）
A．B．1C．D．
【答案】C
【分析】根据空间向量的加法、减法、数乘运算即可求解.
【详解】
如图，
,
所以，
所以，
故选:C.
4．（2023·福建师大附中高二期末）如图所示，在平行六面体ABCD－A1B1C1D1中，M为A1C1与B1D1的交点.若，，，则下列向量中与相等的向量是（ ）.
A．B．
C．D．
【答案】A
【分析】根据空间向量线性运算的定义进行求解即可.
【详解】，
故选：A
考点二 共线问题
5．（2023·全国·高二期末）已知空间向量，，且，，，则一定共线的三点是（ ）
A．B．C．D．
【答案】C
【分析】根据向量共线判断三点共线即可．
【详解】解：
，
又与过同一点B，
∴ A、B、D三点共线．
故选：C．
6．（2023·山西吕梁·高二期末）在平行六面体中，点P在上，若，则（ ）
A．B．C．D．
【答案】C
【分析】利用空间向量基本定理，结合空间向量加法的法则进行求解即可.
【详解】因为，
，
所以有，因此，
故选：C
7．（2023·上海松江·高二期末）设是正三棱锥，是的重心，是上的一点，且，若，则为（ ）
A．B．
C．D．
【答案】A
【分析】如图所示,连接AG1交BC于点M，则M为BC中点,利用空间向量的运算法则求得，即得.
【详解】如图所示,连接AG1交BC于点M,则M为BC中点，
)=,
.
因为
所以=3(),
∴ .
则，
∴ ，，，
故选：A.
考点三 共面问题
8．【多选】（2023·广东江门·高二期末）若构成空间的一个基底，则下列向量共面的是（ ）
A．B．
C．D．
【答案】ABD
【分析】根据空间向量的共面定理判断即可.
【详解】A：，A是；
B: ，B是；
C：构成空间的一个基底，故无法用表示，C不是；
D：，D是；
故选：ABD
9．（2023·山东·巨野县第一中学高二期末）对于空间一点O和不共线三点A，B，C，且有，则（ ）
A．O，A，B，C四点共面B．P，A，B，C四点共面
C．O，P，B，C四点共面D．O，P，A，B，C五点共面
【答案】B
【分析】利用向量加减法，根据空间向量的加减法，可得三个向量共面，可得答案.
【详解】由，得，
即，故共面.
又因为三个向量有同一公共点，所以共面.
故选：B.
10．（2023·上海市建平中学高二期末）已知A､B､C､D､E是空间中的五个点，其中点A､B､C不共线，则“平面ABC”是“存在实数x､y，使得的（ ）
A．充分而不必要条件B．必要而不充分条件
C．充分必要条件D．既不充分也不必要条件
【答案】A
【分析】根据充分条件、必要条件的定义结合向量共面的判定定理即可得出答案.
【详解】若平面ABC，则共面，故存在实数x､y，使得.
若存在实数x､y，使得，则，，共面
则平面ABC或平面ABC.
所以“平面ABC”是“存在实数x､y，使得的充分而不必要条件.
故选：A.
11．（2023·福建厦门·高二期末）已知是空间的一个基底，，，，若四点共面．则实数的值为（ ）
A．B．C．D．
【答案】A
【分析】由共面定理列式得，再根据对应系数相等计算.
【详解】因为四点共面，设存在有序数对使得，则，即，所以得.
故选：A
12．（2023·江西·临川一中高二期末（理））已知空间向量，，，若，，共面，则m＋2t＝（ ）
A．－1B．0C．1D．－6
【答案】D
【分析】根据向量共面列方程，化简求得.
【详解】，所以不共线，
由于，，共面，
所以存在，使，
即，
，
，
，，
即.
故选：D
13．（2023·全国·高二期末）已知，，，若P，A，B，C四点共面，则λ=___________.
【答案】
【分析】由已知可得共面，根据共面向量的基本定理，即可求解.
【详解】由P，A，B，C四点共面，可得共面，
，
，解得.
故答案为：
考点四 空间向量基本定理
14．（2023·重庆长寿·高二期末）如图，在斜棱柱中，AC与BD的交点为点M，，，，则（ ）
A．B．
C．D．
【答案】A
【分析】根据空间向量的线性运算用表示出即可得．
【详解】-＝，
.
故选：A．
15．（2023·天津市第九十五中学益中学校高二期末）在四棱锥中，底面ABCD是正方形，E为PD中点，若，，，则（ ）
A．B．
C．D．
【答案】C
【分析】根据向量线性运算法则计算即可.
【详解】
．
故选：C．
16．（2023·河南郑州·高二期末（理））已知三棱锥O—ABC，点M，N分别为线段AB，OC的中点，且，，，用，，表示，则等于（ ）
A．B．C．D．
【答案】A
【分析】利用空间向量基本定理进行计算.
【详解】.
故选：A
17．（2023·江苏无锡·高二期末）定义：设是空间的一个基底，若向量，则称有序实数组为向量在基底下的坐标．已知是空间的单位正交基底， 是空间的另一个基底，若向量在基底下的坐标为．
(1)求向量在基底下的坐标；
(2)求向量在基底下的模．
【答案】(1)
(2)
【分析】（1）根据向量在基底下的坐标为，得出向量在基底下的坐标；
（2）根据向量在基底下的坐标直接计算模即可．
(1)
因为向量在基底下的坐标为，
则 ，
所以向量在基底下的坐标为.
(2)
因为向量在基底下的坐标为，
所以向量在基底下的模为.
考点五 空间向量的数量积及其性质的应用
18．（2023·广西钦州·高二期末（理））如图，正四棱柱是由四个棱长为1的小正方体组成的，是它的一条侧棱，是它的上底面上其余的八个点，则集合的元素个数（ ）
A．1B．2C．4D．8
【答案】A
【分析】用空间直角坐标系看正四棱柱，根据向量数量积进行计算即可.
【详解】建立空间直角坐标系，为原点，正四棱柱的三个边的方向分别为轴、轴和轴，
如右图示
，，设，
则AB⃑⋅APi⃑=0,0,1·xpi,ypi,zpi=zpi=1
所以集合，元素个数为1.
故选：A.
19．（2023·福建省华安县第一中学高二期末）三棱锥中，，，，则______．
【答案】-2
【分析】根据向量的减法运算，结合数量积的运算，可求得答案.
【详解】由题意得，故，

,
故答案为：-2
20．（2023·河南焦作·高二期末（理））已知在四面体ABCD中，，，则______．
【答案】24
【分析】由线段的空间关系有，应用向量数量积的运算律及已知条件即可求.
【详解】由题设，可得如下四面体示意图，
则，
又，，
所以.
故答案为：24
21．（2023·河南新乡·高二期末（理））已知空间向量，，，则（ ）
A．B．C．D．
【答案】A
【分析】根据向量的数量积的运算公式，求得，结合，即可求解.
【详解】由题意，空间向量，，，
可得，
则.
故选：A.
22．（2023·北京昌平·高二期末）已知正三棱锥的底面的边长为2，M是空间中任意一点，则的最小值为（ ）
A．B．C．D．
【答案】A
【分析】利用转化法求向量数量积的最值即可.
【详解】解：设中点为,连接,设中点为,则
,
当与重合时，取最小值0.此时有最小值，
故选：A
23．（2023·江苏省扬州市教育局高二期末）如图，平行六面体的底面是边长为1的正方形，且，，则线段的长为（ ）
A．B．C．D．
【答案】B
【分析】先以为基底表示空间向量，再利用数量积运算律求解.
【详解】解：，
，
，
，
所以，
故选：B
24．（2023·江苏宿迁·高二期末）四面体中，，则（ ）
A．B．C．D．
【答案】C
【分析】根据空间向量数量积的运算律及定义计算可得；
【详解】解：因为，，所以
所以，
所以，又，所以，
所以，因为，所以；
故选：C
25．（2023·福建厦门·高二期末）在四面体OABC中，，，，则与AC所成角的大小为（ ）
A．30°B．60°C．120°D．150°
【答案】B
【分析】以为空间的一个基底，求出空间向量求的夹角即可判断作答.
【详解】在四面体OABC中，不共面，则，令，
依题意，，
设与AC所成角的大小为，则，而，解得，
所以与AC所成角的大小为.
故选：B
26．（2023·全国·高二期末）已知，，，，点在直线上运动，当取最小值时，点的坐标是______
【答案】
【分析】先利用向量共线定理设出Q点坐标，再利用向量的数量积运算得到关于的函数式，利用二次函数求最值即可得到答案.
【详解】因为点在直线上运动，所以存在，使得，
因为，所以，所以点的坐标为.
所以，，
所以，
所以当时，取最小值，此时点的坐标为.
故答案为：.
27．【多选】（2023·湖北黄冈·高二期末）棱长为2的正方体的侧面(含边界)内有一动点，则（ ）
A．若，则
B．若，则
C．若，则
D．若，则存在非零向量使
【答案】BCD
【分析】对于每一个选项中所出现的向量用基底表示，然后通过分析或计算数量积就可以对每一个选项进行判断.
【详解】对于A，，
则
，
从而可知点在线段上，由于不垂直侧面，故不成立，所以A错误；
对于B，易证，，从而可知平面，
由，可知点在线段上，因此，所以，B正确；
对于C，
，故C正确；
对于D，设，
所以
，得，从而可知不会是零向量，故D正确.
故选：BCD
考点六 空间向量的运算的坐标表示
空间向量坐标的基本运算
28．（2023·内蒙古乌兰察布·高二期末（理））已知向量，则（ ）
A．B．C．D．
【答案】B
【分析】根据向量加减法运算的坐标表示即可得到结果
【详解】
故选：B.
29．（2023·重庆九龙坡·高二期末）在空间直角坐标系中，若，，则点B的坐标为（ ）
A．（3，1，﹣2）B．（-3，1，2）C．（-3，1，-2）D．（3，-1，2）
【答案】C
【分析】利用点的坐标表示向量坐标，即可求解.
【详解】设，，
，
所以，，，解得：，，，
即.
故选：C
30．（2023·福建宁德·高二期末）已知，，，则的坐标为______．
【答案】
【分析】由向量的坐标表示可得，再根据向量坐标的线性运算求的坐标.
【详解】由题设，，
所以.
故答案为：
31．（2023·陕西·绥德中学高二期末（理））若, ,则与同方向的单位向量是_______.
【答案】
【分析】先由已知求出的坐标，再除以可得答案
【详解】因为,，
所以
所以与同方向的单位向量为，
故答案为：
32．【多选】（2023·福建三明·高二期末）已知正方体的棱长为2，建立如图所示的空间直角坐标系，则（ ）
A．点的坐标为（2，0，2） B．
C．的中点坐标为（1，1，1） D．点关于y轴的对称点为（－2，2，－2）
【答案】BCD
【分析】根据空间直角坐标系，可求点的坐标，由此判断A;求出的坐标，可判断B;
利用中点坐标公式求得的中点坐标，可判断C;根据空间点关于坐标轴的对称点的特点可判断D.
【详解】根据题意可知点的坐标为，故A错误；
由空间直角坐标系可知： ,故B正确；
由空间直角坐标系可知：,故的中点坐标为（1，1，1），故C正确；
点坐标为，关于于y轴的对称点为（－2，2，－2），故D正确，
故选：BCD
空间向量平行的坐标运算
33．（2023·河南焦作·高二期末（理））已知向量，，且，则的值为（ ）
A．B．C．或D．或
【答案】C
【分析】根据空间向量平行的性质得，代入数值解方程组即可.
【详解】因为，所以，所以，
所以，解得或.
故选：C.
34．（2023·浙江·杭州四中高二期末）已知向量，，且与互相平行，则（ ）
A．B．C．D．
【答案】D
【分析】由空间向量共线的坐标表示求解
【详解】，，
则，解得，
故选：D
35．（2023·北京昌平·高二期末）已知是直线的方向向量，是直线的方向向量．若直线，则________．
【答案】
【分析】由，则，从而可得出的值，得出答案.
【详解】由，则
由，
则，解得
所以
故答案为：
36．（2023·重庆长寿·高二期末）已知是直线l的方向向量，为平面的法向量，若，则y的值为（ ）
A．B．
C．D．4
【答案】D
【分析】根据得，计算得解.
【详解】因为，所以，所以，计算得.
故选：D.
空间向量垂直的坐标运算
37．（2023·广东广州·高二期末）已知向量，，若，则实数m的值是___________.
【答案】
【分析】结合已知条件和空间向量的数量积的坐标公式即可求解.
【详解】因为，
所以，解得.
故答案为：.
38．【多选】（2023·福建福州·高二期末）已知空间向量，且，则 （ ）
A．B．C．D．
【答案】AC
【分析】根据空间向量，可由，解得答案.
【详解】由可得：，
即 ，解得 ，
又|b⃑|=(−2)2+1+22=3，
故选：AC.
39．（2023·河北保定·高二期末）已知，，若，则实数______．
【答案】2
【分析】由向量垂直的坐标公式得出实数.
【详解】解析：∵，，∴=，
∵，
故答案为：
40．（2023·黑龙江·哈尔滨工业大学附属中学校高二期末（文））已知向量a→=(1，1，k)，b→=(−1，0，−1)，c→=(0，2，1)，且向量与互相垂直，则的值是（ ）
A．B．C．D．
【答案】D
【分析】根据向量的坐标运算和向量垂直数量积为0可解.
【详解】解：根据题意，易得a→−2b→=(1， 1， k)−2(−1， 0， −1)=(3， 1， k+2)，
∵ 与两向量互相垂直，∴ 0+2+k+2=0，解得.
故选：D
空间向量模长的坐标运算
41．（2023·湖北·黄石市有色第一中学高二期末）若点，，点在轴上，且则______.
【答案】
【解析】设出D的坐标，求出的坐标，根据向量的垂直关系求出答案即可.
【详解】因为点在轴上，可设D（0,0，m）
故
因为，所以，解得：m=6.
故.
故答案为：
42．（2023·天津市滨海新区塘沽第一中学高二期末）已知向量，，若与垂直，则___________.
【答案】
【分析】根据与垂直，可知，根据空间向量的数量积运算可求出的值，结合向量坐标求向量模的求法，即可得出结果.
【详解】解：与垂直，，
则，解得：，
，
则，
.
故答案为：.
43．（2023·江苏·南京市大厂高级中学高二期末）向量，，，且，，则______.
【答案】
【分析】利用向量平行、垂直的坐标表示求出x，y，再利用坐标求出向量的模作答.
【详解】因，，而，则有，解得，即
又，且，则有，解得，即，
于是得，，
所以.
故答案为：
44．（2023·江苏·沭阳如东中学高二期末）已知，则的最小值（ ）
A．B．C．D．
【答案】B
【分析】根据空间向量模长的坐标求解，结合二次函数的最小值，即可求得结果.
【详解】由题可知，，
故，
即的最小值.
故选：B.
空间向量夹角的坐标运算
45．（2023·吉林辽源·高二期末）已知空间向量，是单位向量，，则向量与的夹角为______.
【答案】
【分析】根据空间向量的几何意义求出向量的模，利用数量积的定义计算即可得出夹角.
【详解】，，
因为，
所以，
所以，
由，得向量与的夹角为.
故答案为：
46．（2023·全国·高二期末）若向量，，，夹角为钝角，则的取值范围是______.
【答案】
【解析】根据向量与的夹角为钝角，则·<0，求得λ的范围，在将与共线且反向的情况排除即可.
【详解】∵向量与的夹角为钝角，
∴·＝
解得.
当与共线时，设＝k (k<0)，
可得，
解得，
即当时，向量与共线且反向，
此时·<0，但与的夹角不是钝角.
综上：λ的取值范围是.
故答案为：
47．（2023·江苏淮安·高二期末）如图，在四棱锥P－ABCD中，底面ABCD为正方形，PA⊥平面ABCD，，M为PC上一动点，，若∠BMD为钝角，则实数t可能为（ ）
A．B．C．D．
【答案】D
【分析】建立空间直角坐标系，利用即可求解.
【详解】分别以、、为轴，轴，轴建立空间直角坐标系，如图所示，
设， ，故，,，,
由可知，，即，
又因为为钝角，所以，
由,,可知，，
，整理得，
解得，
故选：D.
48．（2023·广东江门·高二期末）若两个单位向量与向量的夹角都等于，则__________.
【答案】
【分析】根据已知可得，，利用完全平方公式求得，再根据即可求得答案.
【详解】因为两个单位向量与向量的夹角都等于，
，，，
，，
又，则，
，即，
，
.
故答案为：.
空间向量投影的坐标运算
49．（2023·上海金山·高二期末）在空间直角坐标系 中，已知向量，则 在轴上的投影向量为________.
【答案】
【分析】根据向量坐标意义及投影的定义得解.
【详解】因为向量，所以 在轴上的投影向量为.
故答案为:
50．（2023·天津天津·高二期末）已知空间向量，，则向量在向量上的投影向量的坐标是__________．
【答案】
【分析】根据投影向量概念求解即可.
【详解】因为空间向量，，
所以，，
所以向量在向量上的投影向量为：
，
故答案为：.
51．（2023·广东惠州·高二期末）已知，，则在上的投影向量为（ ）
A．1B．C．D．
【答案】C
【分析】根据题意得，进而根据投影向量的概念求解即可.
【详解】解：因为，，所以，
所以，
所以在上的投影向量为
故选：C
考点七 空间向量在立体几何平行、垂直问题中的应用
平行问题
52．（2023·黑龙江·哈尔滨工业大学附属中学校高二期末（文））如图，已知四棱锥的底面是矩形，平面分别是棱的中点．
(1)求证：∥平面；
(2)求平面与平面夹角的大小．
【答案】(1)证明见详解；
(2)
【分析】（1）如图建立空间直角坐标系，求出平面的法向量，然后与法向量垂直可证；（2）分别求出两个平面的法向量再根据平面与平面夹角公式可求得.
【详解】（1）
如图建系，
设平面的法向量为
所以不妨取
又
又平面，∥平面；
（2）由（1）知：,
设平面的法向量为，平面的法向量
所以不妨取
同理不妨取
设平面与平面夹角为
所以
53．（2023·安徽滁州·高二期末）如图，在多面体ABCDEF中，AD⊥平面ABC，AD//BE//CF，且AD＝1，BE＝5，CF＝3，△ABC是边长为2的正三角形，G是AB的中点．
(1)求证：CG//平面DEF；
(2)求二面角的余弦值．
【答案】(1)见解析
(2)
【分析】（1）以B为坐标原点，BA所在直线为x轴，在平面ABC中，过B作AB的垂线为y轴，BE所在直线为z轴，建立空间直角坐标系，利用向量法能证明 CG//平面DEF；
（2）求出平面DEF的法向量和平面ADF的法向量，利用向量法能求出二面角的余弦值．
（1）
证明：以B为坐标原点，BA所在直线为x轴，在平面ABC中，过B作AB的垂线为y轴，BE所在直线为z轴，建立空间直角坐标系，
则，
，
设平面DEF的法向量，
则，取x＝2，得，
∵0，所以，
又平面DEF，∴CG//平面DEF；
（2）
解：平面DEF的法向量，
，，
设平面ADF的法向量，
则，取b＝1，得，
则，
有图可知二面角为钝二面角，
所以二面角的余弦值为.
垂直问题
54．（2023·安徽省宿州市第二中学高二期末）如图，边长为2的等边所在的平面垂直于矩形ABCD所在的平面，，M为BC的中点.
(1)证明：；
(2)求平面PAM与平面ABCD的夹角的大小；
(3)求点D到平面AMP的距离.
【答案】(1)证明见解析
(2)
(3)
【分析】（1）以为原点，为轴，为轴，过作平面的垂线为轴，建立空间直角坐标系，利用向量法能证明；
（2）求出平面的法向量和平面的法向量，利用向量法能求出平面与平面夹角的大小；
（3）求出平面的法向量，利用向量法能求出点到平面的距离．
【详解】（1）证明：等边所在的平面垂直于矩形ABCD所在的平面，
以D点为原点，分别以直线DA，DC为x轴、y轴，过D作平面ABCD的垂线为z轴，
建立如图所示的空间直角坐标系，（其他建系方法按步骤给分）
依题意，可得，，，，
，，
，
即，；
（2）解：设为平面PAM的法向量，
则，即，
取，得，
取，显然为平面ABCD的一个法向量，
⟨⟩，
故平面PAM与平面ABCD的夹角的大小为；
（3）解：设点D到平面AMP的距离为d，
由可知与平面PAM垂直，
则，
即点D到平面AMP的距离为
55．（2023·福建福州·高二期末）如图，在正四棱柱中，已知，，E，F分别为，上的点，且．
(1)求证：平面ACF：
(2)求点B到平面ACF的距离．
【答案】(1)证明见详解.
(2).
【分析】（1）以为坐标原点，为轴，为轴，为轴建立空间直角坐标系通过证明与平面的一个法向量重合来证明平面.
（2）利用点面距离公式即可计算出点到平面的距离.
【详解】（1）以为坐标原点，为轴，为轴，为轴建立空间直角坐标系，如下图所示：
则,
设面的一个法向量为，，
可得，即，不妨令则,
平面.
（2），则点到平面的距离为.
56．（2023·湖北恩施·高二期末）在三棱台ABC－A1B1C1中，C1C⊥平面ABC，AB⊥BC，且AB=BC=C1C=2A1B1，O为AC的中点，P是C1C的中点.
(1)证明：平面A1BC⊥平面POB；
(2)求二面角B1－A1B－C的余弦值.
【答案】(1)证明见解析
(2)
【分析】（1）先证明BO⊥AC，以O为坐标原点，以，，的方向分别为x，y，z轴的正方向，建立空间直角坐标系，利用空间向量可得，即可证明；
（2）利用空间向量，分别求解平面A1B1B和平面A1BC的法向量，即可求解二面角B1－A1B－C的余弦值.
(1)
证明：连接A1O设A1B1=1，则AB=BC=C1C=2，AC=，A1C1=
因为C1C⊥平面ABC，O为AC的中点，所以A1O⊥平面ABC,
因为AB=BC，所以BO⊥AC.
以O为坐标原点，以，，的方向分别为x，y，z轴的正方向，建立如图所示的空间直角坐标系O－，
则A(0，－，0)，B(，0，0)，C(0，，0)，(0，0，2)，(，，2)，(0，，2)，P(0，，1).
因为，
所以，
所以A1C⊥OB，A1C⊥OP.
因为，所以A1C⊥平面POB..
因为平面A1BC，
所以平面A1BC⊥平面POB.
(2)
解：由（1）知,
设平面A1B1B的法向量为,
则,令，但,
设平面A1BC的法向量为,
则,令，得,
因为，且二面角为锐角，
所以的余弦值为.
综合问题
57．（2023·浙江·杭州四中高二期末）已知平面法向量为，直线的方向向量为，则（ ）
A．与平行B．与垂直
C．与相交但不垂直D．以上都不对
【答案】B
【分析】利用向量共线判断出为平面的一个法向量，即可判断.
【详解】因为，，
所以，
所以与垂直.
故选：B
58．【多选】（2023·广东深圳·高二期末）直三棱柱中，分别为，的中点，点是棱上一动点，则（ ）
A．对于棱上任意点，有
B．棱上存在点，使得面
C．对于棱上任意点，有面
D．棱上存在点，使得
【答案】AD
【分析】对于A，连接，证明平面即可；对于B，建立空间直角坐标系，判断MN与BN是否可能垂直即可；对于C、D，当N是AC中点时，MN∥DE，即可判断.
【详解】A选项：
连接，由题可知四边形是正方形，则，
由题知平面平面，平面平面，，平面ABC，
∴平面，又，∴，
又，平面，∴平面，
∵平面，∴.
故A正确；
B选项：
如图建立空间直角坐标系，设AC＝BC＝＝2，
则，，，，，设，，则，，
若BN⊥MN，则，即，方程无实数根，即BN与MN不垂直，则不存在点N，使得平面，B错误；
C选项：
当N是AC中点时，MN∥，∥DE，∴MN∥平面；
当N不是AC中点时，MN和B1C相交，若∥平面，结合∥平面可知平面∥平面，这显然与图形不符(与AC相交)，故此时与平面不平行；故C错误；
D选项：
由C项可知，N为AC中点满足题意，故D正确.
故选：AD.
59．（2023·北京房山·高二期末）如图，正方体中，是的中点，则下列说法正确的是（ ）
A．直线与直线垂直，直线平面
B．直线与直线平行，直线平面
C．直线与直线异面，直线平面
D．直线与直线相交，直线平面
【答案】A
【分析】根据空间的平行和垂直关系进行判定.
【详解】连接；由正方体的性质可知，是的中点，所以直线与直线垂直；
由正方体的性质可知，所以平面平面，
又平面，所以直线平面，故A正确；

以为原点，建立如图坐标系，设正方体棱长为1，
显然直线与直线不平行，故B不正确；
直线与直线异面正确，，，所以直线与平面不垂直，故C不正确；
直线与直线异面，不相交，故D不正确；
故选：A.
考点八 空间角的计算
异面直线所成的角
60．（2023·广东江门·高二期末）在直三棱柱中，分別是的中点，，则与所成角的正弦值是（ ）
A．B．C．D．
【答案】C
【分析】建立空间直角坐标系，利用向量法求得所成角的余弦值，从而求得所求.
【详解】根据题意易知两两相互垂直，
由此建立如图所示空间直角坐标系，不妨设，
则
故，，
设所成角为，，
则，
所以，即与所成角的正弦值是.
故选：C.
61．（2023·贵州六盘水·高二期末（理））如图是正方体的平面展开图，则在这个正方体中：
①BM与ED平行
②BM与CE垂直
③CE与平面ABCD所成角的正切值为
④CN与BM所成角为
以上四个命题中，正确命题的序号是（ ）
A．①②B．②③C．②④D．③④
【答案】C
【分析】根据展开图还原正方体，设其棱长为1，建立空间直角坐标系，即可判断异面直线的位置关系，计算出夹角，以及CE与平面ABCD所成角的正弦值，进而求出正切值.
【详解】解：根据平面展开图，还原正方体，并建立空间直角坐标系，如下图所示，
设正方体棱长为1，则，，，，，，
①BM与ED平行，由图可看出BM与ED不平行，错误；
②BM与CE垂直，，
，即，正确；
③CE与平面ABCD所成角的正切值为，
由图可知为平面ABCD的一个法向量，且，
设CE与平面ABCD所成的角为，
则，
，
，错误；
④CN与BM所成角为，
设CN与BM所成角为，
，，
，
，正确；
故选：C.
62．（2023·黑龙江·双鸭山一中高二期末）如图，在四棱锥中，底面为等腰梯形，，，面，，点为线段中点
(1)求证：面；
(2)求异面直线与所成角的大小.
【答案】(1)证明见解析
(2)
【分析】（1）建立直角坐标系，求出平面的法向量，若与平面的法向量的数量积为0，则可证明；
（2）求异面直线所成的角的大小可以根据数量积的计算公式，即可求解.
（1）
证明：
由面建立如图所示的直角坐标系，以A点为坐标原点，分别以，垂直于AD以及为方向建立轴，如图所示:
由底面是等腰梯形以及可知：，，
，
又由点为线段中点，可知
，，
设为平面的法向量，故可知：
，解得
令，可知平面的法向量一个法向量为：
根据线面平行的向量法判断法则可知面
（2）
解：由题意得：由（1）分析可知，
可知向量互相垂直，故异面直线与所成角的大小为
直线与平面所成的角
63．【多选】（2023·山东·巨野县第一中学高二期末）已知在直三棱柱中，底面是一个等腰直角三角形，且，E、F、G、M分别为的中点．则（ ）
A．与平面夹角余弦值为B．与所成角为
C．平面EFBD．平面⊥平面
【答案】BCD
【分析】建系，利用坐标法，根据线面角，线线角的向量求法可判断AB，根据线面平行的判定定理可判断C，利用线面垂直的判定定理先证平面，可得，再证平面，然后根据面面垂直的判定定理即得．
【详解】如图1，建立空间之间坐标系，设，则有：
，
∴，，，，，
设平面ACC1A1的法向量为
则有，令x＝1，则，
则，
∴与平面夹角的正弦值为，则余弦值为，A错误；
∵，
∴AB1与BC1所成角的余弦值为，则夹角为，B正确；
如图2：连接，设，连接OF，
E、M分别为的中点，则且，
∴为平行四边形，则O为的中点，
又∵F为的中点，则，
平面EFB，平面EFB，
∴平面EFB，C正确；
由题可知平面即为平面，
由题意可得：，
又，平面，
∴平面，
平面，则，
又∵为正方形，则，
又，平面，
所以平面，平面，
∴平面⊥平面，即平面⊥平面，D正确.
故选：BCD．
64．（2023·河南南阳·高二期末（理））如图，四边形为直角梯形，且，为正方形，且平面平面，，，，则______，直线与平面所成角的正弦值为______．
【答案】 . .
【分析】以点为坐标原点，，，所在直线分别为轴，轴，轴建立空间直角坐标系,根据空间向量的线性运算求得向量的坐标，由此求得，由线面角的空间向量求解方法求得答案.
【详解】解：以点为坐标原点，，，所在直线分别为轴，轴，轴建立空间直角坐标系（如下图所示）．
由题意可知，，，．
因为，，所以，故．
设平面的法向量为，则，令，得．
因为，所以直线与平面所成角的正弦值为．
故答案为：；.
65．（2023·福建省仙游县度尾中学高二期末）如图，在三棱锥中，是正三角形，，是的中点．
(1)证明：；
(2)求直线与平面所成角的正弦值．
【答案】(1)证明见解析
(2)
【分析】（1）先由三线合一得到，再由中位线定理可得，从而利用线面垂直的判定定理证得面，由此可得；
（2）建立空间直角坐标系，利用及空间两点距离公式求得，从而求得平面的法向量，由此利用向量法即可求得直线与平面所成角的正弦值．
【详解】（1）取的中点，连接，
因为是正三角形，所以，
因为是的中点，所以，
因为所以，
又面，所以面，
又因为面，所以.
.
（2）以为轴､轴，过作轴⊥底面，建立如图空间直角坐标系，
则，
记，又，则，
因为，解得，则，
由易得直线的一个方向向量为，
设平面的法向量为，，
则，令，则平面的一个法向量为，
记直线与平面所成角为，那么.
66．（2023·甘肃·测试·编辑教研五高二期末（理））如图，在直三棱柱中，，，，点，分别在棱，上，且，，为棱的中点.
(1)求证：；
(2)求直线与平面所成角的正弦值.
【答案】(1)证明见解析
(2)
【分析】（1）以为原点，分别以，，的方向为轴、轴、轴的正方向建系，可得点、、、的坐标，进而可得、的坐标，利用数量积公式，即可得证；
（2）求得的坐标和平面的法向量，利用线面角的夹角公式，即可求得结果.
【详解】（1）证明：依题意，以为原点，分别以，，的方向为轴、轴、轴的正方向建立空间直角坐标系，如图所示，
可得，，，，，，，，，
依题意，，，
所以，
所以；
（2）由（1）知，，
设为平面的法向量，
则，即，不妨设，可得，
又，设与平面所成角为，
所以，
直线与平面所成角的正弦值为.
67．（2023·四川绵阳·高二期末（理））如图，在四棱锥中，底面，，，，，为棱的中点，是线段上一动点.
(1)求证：平面平面；
(2)若直线与平面所成角的正弦值为时，求二面角的余弦值.
【答案】(1)证明见解析
(2)
【分析】（1）证明出平面，利用面面垂直的判定定理可证得结论成立；
（2）以点为坐标原点，、、所在直线分别为、、轴建立空间直角坐标系，设，其中，利用已知条件求出的值，然后利用空间向量法可求得二面角的余弦值.
【详解】（1）证明：因为，，则，
平面，平面，，
，、平面，平面，
平面，因此，平面平面.
（2）解：因为底面，，
以点为坐标原点，、、所在直线分别为、、轴建立如下图所示的空间直角坐标系，
则、、、、、，
设，，其中，
易知平面的一个法向量为，
由已知可得，解得，
所以，为的中点，即，
设平面的法向量为，，，
则，取，可得，
易知平面的一个法向量为，
所以，，
由图可知，二面角的平面角为钝角，
故二面角的余弦值为.
平面与平面所成的角（二面角）
68．（2023·青海玉树·高二期末（理））如图,在四棱锥中,平面,,正方形的对角线交于点O．
(1)求证:平面PAC;
(2)求二面角的余弦值．
【答案】(1)证明见解析;
(2)
【分析】(1)由于平面,则,由正方形,则,根据线面平行判定定理即可证明线面垂直;
(2)根据题意建立合适的空间直角坐标系,设,找到点的坐标,求出,再求出平面的法向量,根据题中条件,找到平面法向量,求出法向量夹角的余弦值的绝对值,根据图像判断二面角大小的范围,即可求出其余弦值.
【详解】（1）解:由题知平面,
,
正方形,
,
平面,平面,
平面.
（2）由题知平面,为正方形,
以为坐标原点,方向为轴,方向为轴, 方向为轴建立空间直角坐标系如图所示:
不妨设,,
,
,
记平面法向量为,
,
即,
不妨取,则,
平面,
平面法向量为,
,
由图可知二面角的大小为钝角,
故二面角的余弦值为.
69．（2023·云南曲靖·高二期末）如图所示，⊥平面，四边形为矩形，，.
(1)求证：∥平面；
(2)求平面与平面所成锐二面角的余弦值.
【答案】(1)证明见解析
(2)
【分析】（1）由面面平行判断定理证平面BFC平面ADE，再证∥平面即可；
（2）建立空间直角坐标系如图，由向量法即可求
【详解】（1）证明：四边形为矩形，∴，又，平面，平面ADE，故平面ADE，平面ADE，
又平面BFC，∴平面BFC平面ADE，
∵平面BFC，∴∥平面；
（2）建立空间直角坐标系如图，则，
设平面CDF的法向量为，则，取得，
平面的法向量为，设平面与平面所成锐二面角为，则，
故平面与平面所成锐二面角的余弦值为
70．（2023·广东中山·高二期末）如图，在四棱锥中，底面四边形为直角梯形，，，，，，.
(1)求证：平面平面；
(2)求平面和平面的夹角大小.
【答案】(1)证明见解析；
(2).
【分析】（1）根据线面垂直的判定定理，结合面面垂直的判定定理进行证明即可；
（2）建立空间直角坐标系，利用空间平面向量夹角公式
【详解】（1）如图，过作于.由题意可知，在直角梯形中，，，，所以，.
又，，所以，所以.
因为，又，面，
所以面.
因为面，所以面面；
（2）由（1）可知，，，两两垂直，故可以点为坐标原点，以，，分别为x，y，z轴建立如图所示的空间直角坐标系.
易知，，，，
则，，，
设平面的法向量为，则
令，则，，即，
设平面的法向量为，则
令，则，，即，
所以，即平面和平面的夹角为.
71．（2023·浙江省杭州第九中学高二期末）如图，在三棱锥中，，，为的中点.
(1)证明：平面；
(2)若点在棱上，，且二面角为30°，求的值.
【答案】(1)证明过程见详解
(2)
【分析】（1）由已知可得，求解三角形可得，再由直线与平面垂直的判定可得平面.
（2）以点为原点，分别以所在直线为 轴建立空间直角坐标系,由得到的坐标，进而求出平面的法向量，再由二面角为30°列式求出的值.
（1）
证明：连接 ，且为的中点 且
又 且

又 平面
（2）
如图，以点为原点，分别以所在直线为 轴建立空间直角坐标系.
则,
，点在棱上
设平面的法向量
则 即
令，则
取平面的法向量
二面角为30°
解得或（舍）
故：
考点九 空间距离的计算
点到直线的距离
72．（2023·吉林白山·高二期末）已知，，，则点C到直线AB的距离为（ ）
A．3B．C．D．
【答案】D
【分析】应用空间向量的坐标运算求在上投影长及的模长，再应用勾股定理求点C到直线AB的距离.
【详解】因为，，所以．
设点C到直线AB的距离为d，则
故选：D
73．（2023·安徽省宿州市第二中学高二期末）已知直线经过点，且是的方向向量，则点到的距离为（ ）
A．B．C．D．
【答案】C
【分析】由空间向量夹角的坐标表示求，再根据点到直线距离为即可求结果.
【详解】由题设，则，
所以，而，
故到l的距离为.
故选：C
74．（2023·青海海东·高二期末（理））在正方体中，分别是线段的中点，则点到直线的距离是（ ）
A．B．C．D．
【答案】A
【分析】以为坐标原点，分别以的方向为轴的正方向，建立空间直角坐标系，然后，列出计算公式进行求解即可
【详解】
如图，以为坐标原点，分别以的方向为轴的正方向，建立空间直角坐标系.因为，所以，所以，则点到直线的距离
故选：A
点到平面的距离、直线到平面的距离、平面到平面的距离
75．（2023·上海市奉贤中学高二期末）经过原点的平面的一个法向量为，点坐标为，则点到平面的距离为______.
【答案】
【分析】使用空间向量法求点到平面的距离,点到平面的距离可视为在上的投影大小.
【详解】设坐标原点为,则,点到平面的距离可视为在上的投影大小,
故.
故答案为：
76．（2023·青海·海南藏族自治州高级中学高二期末（理））设正方体的棱长为，则点到平面的距离是（ ）
A．B．C．D．
【答案】D
【分析】建立空间直角坐标系，根据空间向量所学点到面的距离公式求解即可.
【详解】建立如下图所示空间直角坐标系，以为坐标原点，
所在直线为轴，所在直线为轴，所在直线为轴.
因为正方体的边长为4，所以，，，，
，所以，，，
设平面的法向量，所以，，
即，设，所以，，即，
设点到平面的距离为，所以，
故选：D.
77．（2023·江苏·南京师大附中高二期末）在矩形ABCD中，，点E是线段AD的中点，将△ABE沿BE折起到△PBE位置（如图），点F是线段CP的中点．
(1)求证：DF∥平面PBE：
(2)若二面角的大小为，求点A到平面PCD的距离．
【答案】(1)证明见解析；
(2).
【分析】（1）利用线面平行的判定定理即得；
（2）由题建立空间直角坐标系，利用点到平面的距离的向量求法即得.
（1）
设PB的中点为G点，连接GF和GE，
因为点G、点F分别为PB和PC的中点，
所以且，又且，
所以且，
所以四边形GFDE为平行四边形，
所以，又GE平面PBE，DF平面PBE，
所以DF∥平面PBE；
（2）
由二面角的大小为可知，平面平面，
取BE得中点O，连接，则，平面，
如图建立空间直角坐标系，
则，，
所以，
设平面PCD的法向量为，
则，
令则，又，
所以点A到平面PCD的距离为.
78．（2023·浙江省杭州第九中学高二期末）若两平行平面、分别经过坐标原点O和点，且两平面的一个法向量为，则两平面间的距离是______．
【答案】
【分析】根据给定条件，结合平行平面距离的意义，利用空间向量计算作答.
【详解】依题意，平行平面间的距离即为点O到平面的距离，
而，所以平行平面、间的距离.
故答案为：
异面直线的距离
79．（2023·福建·厦门外国语学校高二期末）如图，在正方体中，AB＝1，M，N分别是棱AB，的中点，E是BD的中点，则异面直线，EN间的距离为______.
【答案】
【分析】建立空间直角坐标系，表示出，求出同时垂直于的，再通过公式求距离即可.
【详解】
以为原点，的方向为轴建立空间直角坐标系，易知，
，设同时垂直于，由，令，得，
又，则异面直线，EN间的距离为.
故答案为：.
80．（2023·浙江宁波·高二期末）如图，正四棱锥的棱长均为2，点E为侧棱PD的中点．若点M，N分别为直线AB，CE上的动点，则MN的最小值为______．
【答案】
【分析】根据题意，先建立空间直角坐标系，然后写出相关点的坐标，再写出相关的向量，然后根据点分别为直线上写出点的坐标，这样就得到，然后根据的取值范围而确定
【详解】
建立如图所示的空间直角坐标系，则有：
，，，，，
可得：
设，且
则有：，
可得：
则有：
故
则当且仅当时，
故答案为：
81．（2023·全国·高二期末）在如图所示实验装置中，正方形框架的边长都是1，且平面平面，活动弹子分别在正方形对角线，上移动，则长度的最小值是___________．
【答案】
【分析】将问题转化为异面直线与之间距离的求解问题，以为原点建立空间直角坐标系，根据异面直线间距离的空间向量求法可求得结果.
【详解】是异面直线，上两点，的最小值即为两条异面直线间距离.
平面平面，，平面平面，
平面，又，则以为坐标原点可建立如图所示的空间直角坐标系，
则，，，，
，，，
设异面直线，的公垂向量，
则，令，则，，，
，即的最小值为.
故答案为：.
考点十 空间向量与立体几何的综合问题
82．【多选】（2023·广东茂名·高二期末）（多选）如图，在长方体中，，，是侧面的中心，是底面的中心，以为坐标原点，、、所在直线分别为、、轴建立空间直角坐标系，则（ ）
A．是单位向量
B．三棱锥外接球的表面积为
C．直线与所成角的余弦值为
D．平面
【答案】ABD
【分析】求出，可判断A选项的正误；求出长方体的外接球半径，结合球体的表面积公式可判断B选项的正误；利用空间向量法可判断C选项的正误；利用线面平行的判定定理可判断D选项的正误.
【详解】对于A选项，、，则，A对；
对于B选项，长方体的外接球半径为，
所以，三棱锥外接球和长方体的外接球为同一球，
该球的表面积为，B对；
对于C选项，、，，，
，C错；
对于D选项，，，则，所以，，
平面，平面，故平面，D对.
故选：ABD.
83．【多选】（2023·辽宁辽阳·高二期末）在空间直角坐标系中，，则（ ）
A．
B．点B到平面的距离是2
C．异面直线与所成角的余弦值
D．点O到直线的距离是
【答案】BD
【分析】由已知，选项A，可以通过三点的坐标，直接计算即可验证；选项B，可先求解平面的法向量，然后再利用点到平面距离公式即可求解；选项C，分别表示出异面直线与的方向向量，然后利用向量数量积计算夹角即可；选项D，先计算在上的投影，然后再计算点到直线的距离.
【详解】因为，所以，A错误．
在空间直角坐标系中，结合A与C两点的坐标可知y轴与平面垂直，所以为平面的一个法向量，则点B到平面的距离是，B正确．
因为，所以异面直线与所成角的余弦值为，C错误．
因为，所以，所以点O到直线的距离是．D正确．
故选：BD.
84．【多选】（2023·江苏南通·高二期末）在平行六面体中，，，点在线段上，则（ ）
A．
B．到和的距离相等
C．与所成角的余弦值最小为
D．与平面所成角的正弦值最大为
【答案】BCD
【分析】由结合推出面，得出矛盾，即可判断A选项；由为线段的垂直平分线 ，且，即可判断B选项；由异面直线夹角的求法即可判断C选项；由线面角的求法即可判断D选项．
【详解】
对于A，若，易得四边形为菱形，则，又，面，
可知面，则面，显然矛盾，故A错误；
对于B，其中 点在线段 上， 平分 ，且 为线段的垂直平分线 ，又，
可知 上所有点到 与 的距离相等，故 B 正确 ；
对于C，设平行六面体 的边长为 ，易得 ，其中 ，
可得 ，又，
则与所成角即为，当 点运动到 点处时，此时 最小，即 与 所成角的余弦值最小，
，故 C 正确；
易得当 点运动到 点处时，此时 与平面 所成角最大，即正弦值最大，
又
，则，又，，面，则面，
作，垂足为，则，又面且相交，则面，则即为与平面所成角，
则有 ，故正弦值最大为 ， D 正确．
故选：BCD.
【过关检测】
一、单选题
1．（2023·江苏扬州·高二期中）如图，在平行六面体中，为和的交点，若，，，则下列式子中与相等的是（ ）
A．B．C．D．
【答案】A
【分析】根据空间向量的加减运算，表示出向量，即得答案.
【详解】
,
故选;A
2．（2023·河北·石家庄二十三中高二阶段练习）设直线、的方向向量分别为，，能得到的是（ ）
A．，B．，
C．，D．，
【答案】B
【分析】利用向量垂直的坐标表示，逐一验证各选项中的两个向量即可判断作答.
【详解】对于A，因，，则，A不能；
对于B，因，，则，B能；
对于C，因，，则，C不能；
对于D，因，，则，则D不能.
故选：B
3．（2023·全国·高二专题练习）如图所示，空间四边形ABCD中，点G为的重心，E，F，H分别为边CD，AD和BC的中点，则的化简结果为（ ）
A．B．C．D．
【答案】A
【分析】根据向量的加法运算进行求解.
【详解】∵点G为的重心，
∴
又
∴，
从而
故选：A.
4．（2023·全国·高考真题（理））在正方体中，P为的中点，则直线与所成的角为（ ）
A．B．C．D．
【答案】D
【分析】平移直线至，将直线与所成的角转化为与所成的角，解三角形即可.
【详解】
如图，连接，因为∥，
所以或其补角为直线与所成的角，
因为平面，所以，又，，
所以平面，所以，
设正方体棱长为2，则，
，所以.
故选：D
5．（2023·湖北·武汉市第十七中学高二期中）在正四面体中，点E在棱AB上，满足，点F为线段AC上的动点，则（ ）
A．存在某个位置，使得
B．存在某个位置，使得
C．存在某个位置，使得直线DE与平面DBF所成角的正弦值为
D．存在某个位置，使得平面DEF与平面DAC夹角的余弦值为
【答案】C
【分析】设正四面体的底面中心为点，连接，则平面，以点为坐标原点，、所在直线分别为、轴建立空间直角坐标系，设正四面体的棱长为，然后利用空间向量法逐一分析求解可得结果.
【详解】如下图所示，设正四面体的底面中心为点，连接，则平面，
以点为坐标原点，、所在直线分别为、轴建立空间直角坐标系，
设正四面体的棱长为，
则，，，，，
设，其中，
对于A，若存在某个位置使得，，，
所以，解得，不满足题意，故A错误；
对于B，若存在某个位置使得，，，
则，该方程无解，故B错误；
对于C，设平面的一个法向量为，
，，
由，令，则，
若存在某个位置，使得直线DE与平面DBF所成角的正弦值为，又，
则，
整理得，解得或（舍去），
所以存在，即为的中点，满足题意，故C正确；
对于D，设平面的一个法向量为，
又，，
由，取，得，
设平面的一个法向量为，
，，
由，取，则，
若存在某个位置，使得平面DEF与平面DAC夹角的余弦值为，
则，
整理得，易得，所以该方程无解，故D错误.
故选：C.
二、多选题
6．（2023·广东·普宁市华侨中学高二阶段练习）如图所示，平行六面体中，，以顶点A为端点的三条棱长都为1，且，则下列结论正确的是（ ）
A．B．平面
C．与平面ABCD所成角的余弦值为D．四棱锥的体积为
【答案】ABC
【分析】A.记，，，利用向量法求解判断；B.连接AC，BD，设，连接，，利用线面平行的判定定理判断；C.过点作平面ABCD于点M，得到与平面ABCD所成的角为求解判断；D.由求解判断.
【详解】解：如图所示：
记，，，则，，
∴．
对于A选项，，∴，即，故A选项正确；
对于B选项，连接AC，BD，设，连接，，则由平行六面体可知 ，∴四边形是平行四边形，∴．又平面，平面，∴平面，故B选项正确；
对于C选项，过点作平面ABCD于点M，易知点M在线段AC上，所以与平面ABCD所成的角为．过点M作于点N，连接，MN，则．在中，，，∴．在RtAMN中，，，∴，∴，故C选项正确；
对于D选项，易得在中，，因为平面ABCD，所以，故D选项错误，
故选：ABC．
7．（2023·全国·高二专题练习）已知直三棱柱中，，，O为的中点.点P满足，其中，则（ ）
A．对时，都有
B．当时，直线与所成的角是30°
C．当时，直线与平面所成的角的正切值
D．当时，直线与相交于一点Q，则
【答案】ACD
【分析】建立空间直角坐标系，利用空间向量的垂直关系证明，可判断A；
先计算出夹角的余弦值，然后进行判断，可判断B；
先计算出与平面一个法向量夹角的余弦值，然后即可求解出线面角的正弦值，由此可计算出线面角的正切值，可判断C；
利用中位线对应的平行关系以及线段长度关系进行说明，可判断D.
【详解】以为轴，建立如图所示空间直角坐标系，设，

其中，
因为，所以，
A.因为，
所以，所以，故正确；
B.当时，，所以，
所以直线与所成的角不是，故错误；
C. 当时，，取平面的一个法向量为，
所以，设直线与平面所成的角为，
所以，所以，故正确；
D. 当时，如图所示，为中点，为中点，连接，
所以，所以，故正确；
故选：ACD.
三、填空题
8．（2023·重庆·四川外国语大学附属外国语学校高二阶段练习）在平行六面体中，用向量，，表示______．
【答案】
【分析】由空间向量的加法和减法运算法则即可求解.
【详解】解：，
故答案为：.
9．（2023·江西南昌·高二期末（理））已知正四面体ABCD中，E，F分别是线段BC，AD的中点，点G是线段CD上靠近D的四等分点，则直线EF与AG所成角的余弦值为______．
【答案】
【分析】建立空间直角坐标系，令正四面体的棱长为，即可求出点的坐标，从而求出异面直线所成角的余弦值；
【详解】解：如图建立空间直角坐标系，令正四面体的棱长为，则，所以，所以，所以，，，，，设，因为，所以，所以，所以，，设直线与所成角为，则
故答案为：
四、解答题
10．（2023·全国·高二课时练习）如图，在三棱柱中，平面，，，点为的中点.
（1）求证：平面；
（2）求点到平面的距离.
【答案】（1）证明见解析；（2）.
【分析】（1）根据平面得，再根据几何关系得，进而可证明平面.
（2）由（1）知，，，以为原点建立空间直角坐标系，利用坐标法求解即可得答案.
【详解】解：（1）证明：因为平面，平面，
所以.
在中，，，，
所以.
所以.
因为，，平面，
所以平面.
（2）由（1）知，，，，
如图，以为原点建立空间直角坐标系.
则，，，.
，.
设平面的法向量为，
则即
令，则，，
所以.
又因为，
故点到平面的距离
.
11．（2023·辽宁实验中学高二阶段练习）如图，在平行六面体中，，，，点为线段中点．
(1)求；
(2)求直线与所成角的余弦值．
【答案】(1)
(2)
【分析】(1)首先设，，，得到，再平方即可得到答案；
(2) 由，得，代入计算即可.
（1）
因为在平行六面体中，点在线段上，且满足．
设，，，这三个向量不共面，构成空间的一个基底．
所以．
，
，
．
（2）
由（1）知，，
，，
，
直线与所成角的余弦值为．
12．（2023·广东·顺德一中高二阶段练习）如图，在三棱柱中，平面，分别为的中点，，.
（1）求证：平面；
（2）求二面角的余弦值；
【答案】（1）证明见解析；（2）.
【分析】（1）通过证明，得线面垂直；
（2）建立空间之间坐标系，利用法向量的夹角的余弦值得二面角的余弦值.
【详解】（1）在三棱柱中，
平面，
故四边形为矩形.
又分别为的中点，
，
又，
，
平面，平面
平面.
（2）由（1）知，
由平面，
平面.
如图建立空间直角坐称系.
由题意得，
，
设平面的法向量为，
，
，
令，则，
所以平面的法向量，
又平面的法向量为，
.
所以二面角的余弦值为.
13．（2023·天津·静海一中高二阶段练习）如图，平面，，，，，，，则
（1）求与所成角的余弦值；
（2）求直线与平面所成角的正弦值；
（3）求平面与平面的夹角的余弦值.
【答案】（1）；（2）；（3）.
【分析】（1）如图以为原点，建立空间直角坐标系，求出和的坐标，利用空间向量夹角公式计算即可求解；
（2）求平面的法向量，利用公式计算即可求解；
（3）求平面的法向量，利用空间向量夹角公式计算即可求解.
【详解】因为平面，，所以两两垂直，
以为原点，分别为轴的正方向，建立空间直角坐标系，
所以，，，，
（1），，
所以，
所以直线与所成角的余弦值为；
（2）设平面法向量，，，
则，令，则，
所以，，
设直线与平面所成角为，
则；
（3）设平面法向量，，，
则，令，则
所以，
，
因为平面与平面夹角是锐二面角，所以二面角的余弦值是.
名称
定义
表示法
零向量
规定长度为0的向量叫做零向量
记为0
单位向量
模为1的向量叫做单位向量
|a|＝1或|eq \(AB,\s\up7(―→))|＝1
相反向量
与向量a长度相等而方向相反的向量，叫做a的相反向量
记为－a
共线向量
如果表示若干空间向量的有向线段所在的直线互相平行或重合，那么这些向量叫做共线向量或平行向量．规定：零向量与任意向量平行，即对于任意向量a，都有0∥a
a∥b或eq \(AB,\s\up7(―→))∥eq \(CD,\s\up7(―→))
相等向量
方向相同且模相等的向量称为相等向量．在空间，同向且等长的有向线段表示同一向量或相等向量
a＝b或 eq \(AB,\s\up7(―→))＝eq \(CD,\s\up7(―→))
加法运算
三角形
法则
语言叙述
首尾顺次相接，首指向尾为和
图形叙述
平行四边形法则
语言叙述
共起点的两边为邻边作平行四边形，共起点对角线为和
图形叙述
减法运算
三角形
法则
语言叙述
共起点，连终点，方向指向被减向量
图形叙述
加法运算
交换律
a＋b＝b＋a
结合律
(a＋b)＋c＝a＋(b＋c)
定义
与平面向量一样，实数λ与空间向量a的乘积λa仍然是一个向量，称为空间向量的数乘
几何意义
λ>0
λa与向量a的方向相同
λa的长度是a的长度的|λ|倍
λ<0
λa与向量a的方向相反
λ＝0
λa＝0，其方向是任意的
运算律
结合律
λ(μa)＝(λμ)a
分配律
(λ＋μ)a＝λa＋μa，λ(a＋b)＝λa＋λb
共线(平行)向量
共面向量
定义
表示若干空间向量的有向线段所在的直线互相平行或重合，这些向量叫做共线向量或平行向量
注：规定：零向量与任意向量平行，即对任意向量a，都有0∥a.
平行于同一个平面的向量叫做共面向量
充要条件
共线向量定理：对于空间任意两个向量a，b(b≠0)，a∥b的充要条件是存在实数λ使a＝λb.
注：（1）存在唯一实数，使得；（2）存在唯一实数，使得，则．注意：不可丢掉，否则实数就不唯一．
共面向量定理：若两个向量a，b不共线，则向量p与向量a，b共面的充要条件是存在唯一的有序实数对(x，y)，使p＝xa＋yb.
对空间任一点O，eq \(OP,\s\up7(―→))＝xeq \(OA,\s\up7(―→))＋yeq \(OB,\s\up7(―→)) (x＋y＝1)．
1、空间一点P位于平面ABC内的充要条件：存在有序实数对(x，y),使eq \(AP,\s\up8(→))＝xeq \(AB,\s\up8(→))＋yeq \(AC,\s\up8(→))或对空间任意一点O，有eq \(OP,\s\up8(→))＝eq \(OA,\s\up8(→))＋xeq \(AB,\s\up8(→))＋yeq \(AC,\s\up8(→)).
2、空间中四点共面的充要条件是存在有序实数对，使得对空间中任意一点，都有
用途
共线向量定理的用途：
①判定两条直线平行；（进而证线面平行）
②证明三点共线。
注意：证明平行时，先从两直线上取有向线段表示两个向量，然后利用向量的线性运算证明向量共线，进而可以得到线线平行，这是证明平行问题的一种重要方法。证明三点共线问题，通常不用图形，直接利用向量的线性运算即可，但一定要注意所表示的向量必须有一个公共点。
共面向量定理的用途：
①证明四点共面
②线面平行（进而证面面平行）。
定义
如图，已知两个非零向量a，b，在空间任取一点O，作eq \(OA,\s\up6(→))＝a，eq \(OB,\s\up6(→))＝b，则∠AOB叫做向量a，b的夹角，记作〈a，b〉
范围
0≤〈a，b〉≤π
向量垂直
如果〈a，b〉＝eq \f(π,2)，那么向量a，b互相垂直，记作a⊥b
数乘向量与数量积的结合律
(λa)·b＝λ(a·b)，λ∈R
交换律
a·b＝b·a
分配律
a·(b＋c)＝a·b＋a·c
点的位置
x轴上
y轴上
z轴上
坐标的形式
(x,0,0)
(0，y,0)
(0,0，z)
点的位置
Oxy平面内
Oyz平面内
Ozx平面内
坐标的形式
(x，y,0)
(0，y，z)
(x,0，z)
向量运算
向量表示
坐标表示
加法
a＋b
(a1＋b1，a2＋b2，a3＋b3)
减法
a－b
(a1－b1，a2－b2，a3－b3)
数乘
λa
(λa1，λa2，λa3)
数量积
a·b
a1b1＋a2b2＋a3b3
设u1，u2分别是直线l1，l2的方向向量，n1，n2分别是平面α，β的法向量．
线线平行
l1∥l2⇔u1∥u2⇔∃λ∈R，使得u1＝λu2
注：此处不考虑线线重合的情况．但用向量方法证明线线平行时，必须说明两直线不重合
证明线线平行的两种思路：①用基向量表示出要证明的两条直线的方向向量，通过向量的线性运算，利用向量共线的充要条件证明．②建立空间直角坐标系，通过坐标运算，利用向量平行的坐标表示．
线面平行
l1∥α⇔u1⊥n1⇔u1·n1＝0
注：证明线面平行时，必须说明直线不在平面内；
(1)证明线面平行的关键看直线的方向向量与平面的法向量垂直．
(2)特别强调直线在平面外．
面面平行
α∥β⇔n1∥n2⇔∃λ∈R，使得n1＝λn2
注:证明面面平行时，必须说明两个平面不重合．
(1)利用空间向量证明面面平行，通常是证明两平面的法向量平行．
(2)将面面平行转化为线线平行然后用向量共线进行证明．
线线垂直
l1⊥l2⇔u1⊥u2⇔u1·u2＝0
(1)两直线垂直分为相交垂直和异面垂直，都可转化为两直线的方向向量相互垂直．
(2)基向量法证明两直线垂直即证直线的方向向量相互垂直，坐标法证明两直线垂直即证两直线方向向量的数量积为0.
线面垂直
l1⊥α⇔u1∥n1⇔∃λ∈R，使得u1＝λn1
（1）基向量法：选取基向量，用基向量表示直线所在的向量，证明直线所在向量与两个不共线向量的数量积均为零，从而证得结论．
（2）坐标法：建立空间直角坐标系，求出直线方向向量的坐标，证明直线的方向向量与两个不共线向量的数量积均为零，从而证得结论．
（3）法向量法：建立空间直角坐标系，求出直线方向向量的坐标以及平面法向量的坐标，然后说明直线方向向量与平面法向量共线，从而证得结论．
面面垂直
α⊥β⇔n1⊥n2⇔n1·n2＝0
(1)常规法：利用面面垂直的判定定理转化为线面垂直、线线垂直去证明．
(2)法向量法：证明两个平面的法向量互相垂直
分类
点到直线的距离
点到平面的距离
图形语言
文字语言
设u为直线l的单位方向向量，A∈l，Pl，eq \(AP,\s\up7(―→))＝a，向量eq \(AP,\s\up7(―→))在直线l上的投影向量为eq \(AQ,\s\up7(―→))
（eq \(AQ,\s\up7(―→))＝(a·u)u.），
则PQ＝eq \r(|eq \(AP,\s\up7(―→))|2－|eq \(AQ,\s\up7(―→))|2)＝eq \r(a2－a·u2)
设已知平面α的法向量为n，A∈α，Pα，向量eq \(AQ,\s\up7(―→))是向量eq \(AP,\s\up7(―→))在平面上的投影向量，
PQ＝eq \b\lc\|\rc\|(\a\vs4\al\c1(eq \(AP,\s\up7(―→))·\f(n,|n|)))＝eq \f(|eq \(AP,\s\up7(―→))·n|,|n|)
注：实质上，n是直线l的方向向量，点P到平面α的距离就是eq \(AP,\s\up6(→))在直线l上的投影向量eq \(QP,\s\up6(→))的长度．
角的分类
向量求法
范围
异面直线所成的角
设两异面直线所成的角为θ，两直线的方向向量分别为u，v，则
cs θ＝|cs〈u，v〉|＝eq \f(|u·v|,|u||v|)
两异面直线所成角的范围是eq \b\lc\(\rc\](\a\vs4\al\c1(0，\f(π,2)))
两异面直线所成的角与其方向向量的夹角是相等或互补的关系．
直线与平面所成的角
设直线l与平面α所成的角为θ，l的方向向量为u，平面α的法向量为n，则
sin θ＝|cs〈u，n〉|＝eq \f(|u·n|,|u||n|)
(1)线面角的范围为eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,2))).
(2)直线与平面所成的角等于其方向向量与平面法向量所成锐角的余角．
两平面的夹角
平面α与平面β相交，形成四个二面角，把不大于eq \f(π,2)的二面角称为这两个平面的夹角．设平面α与平面β的夹角为θ，两平面α，β的法向量分别为n1，n2，则cs θ＝|cs〈n1，n2〉|＝eq \f(|n1·n2|,|n1||n2|)
(1)两个平面的夹角的范围是eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,2)))
(2)两平面的夹角是两法向量的夹角或其补角．