


- 考点巩固卷05 指对幂函数(十一大考点)-备战2024年高考数学一轮复习高分突破(新高考通用) 试卷 1 次下载
- 考点巩固卷06 函数的图象与方程(十大考点)-备战2024年高考数学一轮复习高分突破(新高考通用) 试卷 1 次下载
- 考点巩固卷08 利用导数研究函数的单调性、极值和最值( 十一大考点)-备战2024年高考数学一轮复习高分突破(新高考通用) 试卷 1 次下载
- 考点巩固卷09 三角函数的运算(十大考点)-备战2024年高考数学一轮复习高分突破(新高考通用) 试卷 1 次下载
- 考点巩固卷10 三角函数的图象及性质(十一大考点)-备战2024年高考数学一轮复习高分突破(新高考通用) 试卷 1 次下载
考点巩固卷07 导数的概念、运算及其几何意义(八大考点)-备战2024年高考数学一轮复习高分突破(新高考通用)
展开考点01:导数的定义
1.设函数可导且在处的导数值为1,则______.
【答案】
【分析】根据给定条件,利用导数的定义直接计算作答.
【详解】依题意,,
所以.
故答案为:.
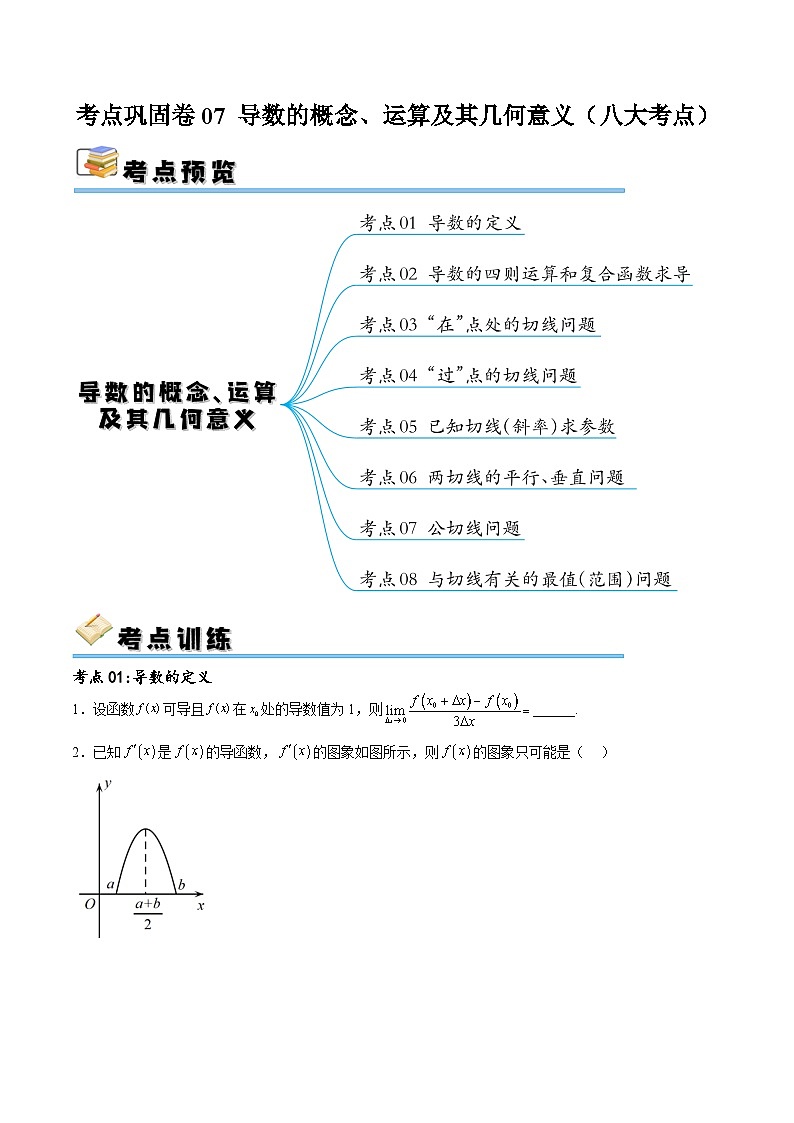
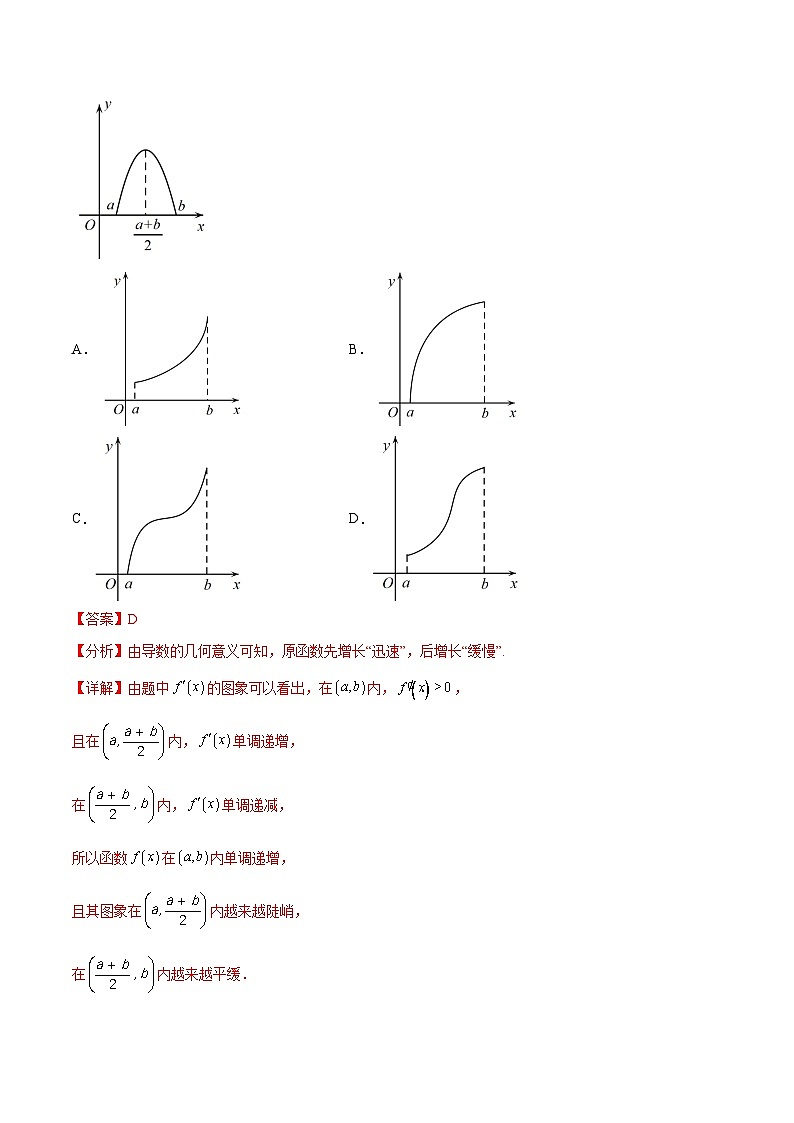
2.已知是的导函数,的图象如图所示,则的图象只可能是( )
A.B.
C.D.
【答案】D
【分析】由导数的几何意义可知,原函数先增长“迅速”,后增长“缓慢”.
【详解】由题中的图象可以看出,在内,,
且在内,单调递增,
在内,单调递减,
所以函数在内单调递增,
且其图象在内越来越陡峭,
在内越来越平缓.
故选:D.
3.若,则函数在处可导是函数在可导的( ).
A.充要条件B.充分非必要条件
C.必要非充分条件D.既非充分又非必要条件
【答案】C
【分析】利用定义法直接判断.
【详解】充分性:函数在处可导不能推出函数在可导.故充分性不满足;
必要性:因为函数在可导,,所以函数在可导.必要性满足.
故函数在处可导是函数在可导的必要非充分条件.
故选:C
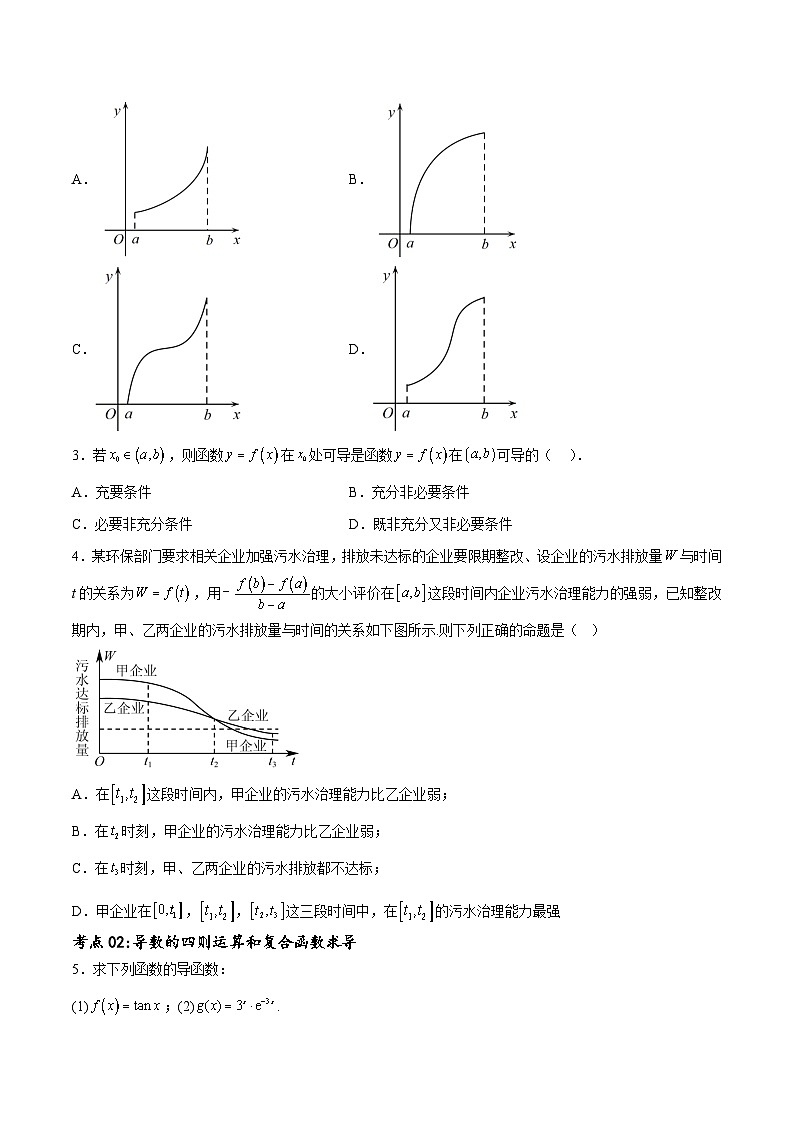
4.某环保部门要求相关企业加强污水治理,排放未达标的企业要限期整改、设企业的污水排放量与时间t的关系为,用的大小评价在这段时间内企业污水治理能力的强弱,已知整改期内,甲、乙两企业的污水排放量与时间的关系如下图所示.则下列正确的命题是( )
A.在这段时间内,甲企业的污水治理能力比乙企业弱;
B.在时刻,甲企业的污水治理能力比乙企业弱;
C.在时刻,甲、乙两企业的污水排放都不达标;
D.甲企业在,,这三段时间中,在的污水治理能力最强
【答案】D
【分析】根据题目中的数学模型建立关系,比较甲乙企业的污水治理能力.
【详解】设甲企业的污水排放量与时间t的关系为,乙企业的污水排放量与时间t的关系为.
对于A选项,在这段时间内,甲企业的污水治理能力,
乙企业的污水治理能力.由图可知,,
所以,即甲企业的污水治理能力比乙企业强,故A选项错误;
对于B选项,由图可知, 在时刻的切线斜率小于在时刻的切线斜率,
但两切线斜率均为负值,故在时刻甲企业的污水治理能力比乙企业强,故B选项错误;
对于C选项,在时刻,甲、乙两企业的污水排放都小于污水达标排放量,
故甲、乙两企业的污水排放都达标,故C选项错误;
对于D选项,由图可知,甲企业在,,这三段时间中,
在时的差值最大,所以在时的污水治理能力最强,故D选项正确,
故选:D.
考点02:导数的四则运算和复合函数求导
5.求下列函数的导函数:
(1);
(2).
【答案】(1)
(2)
【分析】(1)利用函数求导的除法法则运算即可;
(2)利用函数求导的乘法法则运算即可;
【详解】(1),
(2)
6.求下列函数的导数
(1);
(2).
【答案】(1);
(2).
【分析】(1)利用和的导数运算法则求导得解;
(2)利用商的导数运算法则求导得解.
【详解】(1)因为,则.
(2)由题得===-.
7.求下列函数的导数.
(1);
(2).
【答案】(1)
(2)
【分析】(1)根据简单复合函数的求导法则计算可得;
(2)根据导数的运算法则计算可得.
【详解】(1)因为,所以.
(2)因为,所以.
8.(多选)下列求导正确的是( )
A.B.
C. D.
【答案】BD
【分析】根据基本初等函数的导数的运算公式和导数的运算法则,逐项判定,即可求解.
【详解】由基本初等函数的导数的运算公式和导数的运算法则,可得:
对于A中,由,所以A错误;
对于B中,由,所以B正确;
对于C中,由,所以C错误;
对于D中,由,所以D正确.
故选:BD.
9.求下列函数的导函数
(1);
(2);
(3).
【答案】(1)
(2)
(3)
【分析】(1)根据基本初等函数导数公式和导数四则运算法则求解;
(2)设,利用复合函数求导法则求解;
(3)化简函数解析式,设,利用复合函数求导公式求解.
【详解】(1)因为,
所以;
(2)函数可看做函数和的复合函数,
由复合函数求导法则可得,
(3)可化为,
函数可看做函数和的复合函数,
由复合函数求导法则可得,
10.已知下列四个命题,其中正确的个数有( )
① , ② , ③ , ④.
A.0个B.1个
C.2个D.3个
【答案】A
【分析】根据求导公式及运算律,简单复合函数导数逐项求导验证即可
【详解】因为,所以①错,
因为,所以②错,
因为,所以③错.
因为,所以④错,
故选:A.
考点03:“在”点处的切线问题
11.已知函数的图像在点处的切线为l,若l与函数的图像也相切,切点为,则___________.
【答案】9
【分析】先求出,求出切线方程,进而求得,即可求解.
【详解】由题意得,则,
所以切线l的方程为,即.
所以,则,.
故答案为:9.
12.已知是实数,函数,若,则曲线在点处的切线方程是_________.
【答案】
【分析】求导后根据求得,再求得切点坐标和斜率,从而可求解.
【详解】函数的导数为,
,即为,
解得,即,
可得曲线在点处的切线斜率为3 ,切点为,
所以切线的方程为,即为.
故答案为:.
13.已知函数,则函数的图象在点处的切线斜率为( )
A.B.C.D.
【答案】A
【分析】对函数求导,将代入求出的值即可.
【详解】由题设,则,故,
故在点处的切线斜率为.
故选:A
14.直线是曲线在处的切线方程,则( )
A.B.C.D.
【答案】B
【分析】求导,利用切点处的导数值为切线斜率,进而把切点代入切线方程可求解.
【详解】由得,所以,
当时,,故切点为,由于切点在上,所以,故,
故选:B
15.曲线在点处的切线方程为______.
【答案】
【分析】根据求导公式和导数几何意义和直线方程的点斜式求法即可求解.
【详解】因为,
所以 ,
则,
又,
所以曲线在点处的切线方程为,
即.
故答案为:.
16.已知函数,其图象在点处的切线方程为,则它在点处的切线方程为_________.
【答案】
【分析】根据在处的切线方程为可得,且,根据的解析式和导数可求和,从而可求得结果.
【详解】∵在点处的切线方程为,
∴,且,
又,
∴,且,
∴点为,在处切线斜率为,
∴所求切线方程为,即.
故答案为:.
考点04:“过”点的切线问题
17.过点作曲线的切线,则切点的横坐标为_______________,这条切线在x轴上的截距为_______________.
【答案】
【分析】设出切点坐标为,利用导数的几何意义可得切线斜率为,再由两点间斜率公式可得,解得,即可求得切线方程,进而得出结果.
【详解】设切点坐标为,
因为,所以,
即,解得,
所以切线方程为,
可知该切线在x轴上的截距为.
故答案为:,
18.求过且与曲线相切的直线方程.
【答案】或.
【分析】设切点是,由求导可得,再利用导数的几何意义结合斜率公式可得,解得 或,进而可求切线斜率,再利用点斜式即可求解.
【详解】点不在曲线上,
点不是切点,设切点是,
由,可得,
,即 ,
解得 或,
切线的斜率或 ,
切线的方程是或 ,即或.
19.若直线为曲线的一条切线,则实数的值是__________.
【答案】
【分析】根据导数的几何意义、导数的运算公式以及切线方程的求法求解.
【详解】由,可得,
设切点为,则,
故切线方程为,即,
又因为切线为,所以,
解得,所以,
故答案为:.
20.(多选)过点且与曲线相切的直线方程为( )
A.B.
C.D.
【答案】BC
【分析】设出切点,利用导数的几何意义得出切线方程为,再利用条件得到方程,从而求出,进而可求出切线方程.
【详解】设切点为,因为,所以,故切线方程为,
又因为切线过点,所以,整理得,解得或,
当时,切线方程为,即,
当,切线方程为,即.
故选:BC.
21.已知函数,其导函数为,则曲线过点的切线方程为______.
【答案】或
【分析】设切点为,对函数进行求导,且代入可得,故可由点斜式得到切线方程,将代入即可求得或,即可求得切线方程
【详解】设切点为,由,得,
∴,得,∴,,
∴切点为,,
∴曲线在点M处的切线方程为①,
又∵该切线过点,∴,解得或.
将代入①得切线方程为;
将代入①得切线方程为,即.
∴曲线过点的切线方程为或.
故答案为:或
22.若曲线有两条过的切线,则a的范围是______.
【答案】
【分析】由题可将曲线有两条过的切线转化为函数图象与直线有两个交点.后利用导数研究单调性,画出大致图象,即可得答案.
【详解】设切线切点为,因,则切线方程为:.
因过,则,由题函数图象
与直线有两个交点.,
得在上单调递增,在上单调递减.
又,,.
据此可得大致图象如下.则由图可得,当时,曲线有两条过的切线.
故答案为:
考点05:已知切线(斜率)求参数
23.若曲线在点处的切线的斜率为2,则t的值为( )
A.–1B.C.0D.1
【答案】C
【分析】求导解方程即得解.
【详解】由题得,所以.
故选:C
24.已知函数曲线在点处的切线方程为,则a,b的值分别为________.
【答案】1,1
【分析】求出函数的导数,根据导数的几何意义列出相应方程组,即可求得答案.
【详解】由题意可得,.
由于直线的斜率为,且过点,
故,即,解得,
故答案为:1,1
25.已知函数,其中,若曲线在处的切线斜率为1,则的最小值为______.
【答案】/
【分析】根据导数的几何意义可得,再结合基本不等式运算求解.
【详解】因为的定义域为,且,
由题意可得:,
又因为,当且仅当时,等号成立,
所以的最小值为.
故答案为:.
26.若曲线在点处的切线与直线垂直,则的值为( )
A.B.C.D.1
【答案】A
【分析】运用导数几何意义及导数公式求得切线的斜率,结合两直线垂直进而求得a的值.
【详解】由题设,知处的切线的斜率为,
又因为,
所以,解得.
故选:A.
27.已知,为正实数,函数在处的切线斜率为,则的最小值为 ______ .
【答案】
【分析】利用导数的几何意义求得,再根据基本不等式,求最值.
【详解】函数,
所以
因为函数的图象在处的切线斜率为,
所以,
因为,为正实数,
所以,
当且仅当,即时等号成立,
所以的最小值为.
故答案为:.
28.若直线与曲线相切,则_________.
【答案】2
【分析】设切点为,由导数的几何意义可得,令,求导判断单调性,从而可解得.
【详解】设切点为,,则,解得.
令,则,
所以当时,,单调递减;当时,,单调递增.所以,
所以方程的根为.
故答案为:2
考点06:两切线的平行、垂直问题
29.函数在处的切线与直线平行,则实数( )
A.B.1C.D.
【答案】B
【分析】函数在切点处的导数即为切线的斜率,利用直线的平行得到斜率相等,即为关于的方程,可求出的值.
【详解】函数的导函数为 ,
函数在处的切线的导数即为切线的斜率为,
且切线与直线平行,
则有 ,可得 .
故选:B
30.设曲线在点处的切线与直线平行,则实数( )
A.B.
C.D.
【答案】C
【分析】根据导数求解,由两直线平行斜率相等即可求解.
【详解】由得,故,
由于点处的切线与直线平行,且直线的斜率为,所以,
故选:C
31.( 2023秋·江西吉安·高三统考期末)已知函数图像在点和点处的两条切线互相垂直,若,则实数a的范围是________.
【答案】
【分析】假设两切点坐标,得出对应的切线的斜率,分析题意可得,即可解得a的范围.
【详解】解:由题意,则
不妨设,点和点,两切线的斜率分别为,
∴,∴,
∴等价于,
等价于或
解得,或.故a的范围是.
故答案为:.
32.已知函数.若存在,,使得曲线在,处的切线互相垂直,则实数a的取值范围为________.
【答案】
【分析】将化为分段函数并求导,根据导数的几何意义得,即,再由推出,代入可求出结果.
【详解】,,
因为,且,
所以,,
所以,,所以,
所以,又,得,
所以,即.
故答案为:
考点07:公切线问题
33.已知曲线和曲线有唯一公共点,且这两条曲线在该公共点处有相同的切线l,则l的方程为________.
【答案】
【分析】设切点坐标为,根据导数的几何意义可得,即可求得,继而求出切点坐标以及切线斜率,即得答案.
【详解】设曲线和曲线在公共点处的切线相同,
则,
由题意知,
即,解得,
故切点为,切线斜率为,
所以切线方程为,即,
故答案为:
34.已知函数,若曲线与曲线存在公切线,则实数的最大值为__________.
【答案】/0.5
【分析】根据导数的几何意义,利用斜率等于切点处的导数,和切线相同即可判断.
【详解】,
假设两曲线在同一点处相切,
则,可得,即,
因为函数单调递增,且时,
所以,则,此时两曲线在处相切,
根据曲线的变化趋势,若继续增大,则两曲线相交于两点,不存在公切线,
所以的最大值为.
故答案为:.
35.已知函数,若曲线在处的切线也与曲线相切,则______.
【答案】
【分析】求出曲线的切线方程,设曲线的切点坐标为,求出切线斜率,切线方程后,利用两切线重合可得参数值.
【详解】由已知,,又,所以切线方程为,
又,设上切点坐标为,
则,,由得,,
所以,
故答案为:.
36.已知曲线在点处的切线与曲线在点处的切线相同,则( )
A.-1B.-2C.1D.2
【答案】B
【分析】利用导数的几何意义计算即可.
【详解】根据常用函数的导数可知:,,
则两函数在点和处的切线分别为:,化简得
由题意可得:,化简得.
故选:B
37.若直线是曲线的切线,也是曲线的切线,则( )
A.B.C.D.
【答案】D
【分析】设出两个切点坐标,根据导数的几何意义可得.将切点代入两条曲线,联立方程可分别求得,代入其中一条曲线即可求得的值,由此可求.
【详解】直线是曲线的切线,也是曲线的切线,
则两个切点都在直线上,设两个切点分别为
则两个曲线的导数分别为,
由导数的几何意义可知,则
且切点在各自曲线上,所以
则将代入可得
可得
由可得
代入中可知
所以,
所以.
故选:D.
38.若曲线与曲线存在公切线,则实数的最小值为( )
A.B.C.D.
【答案】A
【分析】求出函数的导函数,设公切线与切于点,与曲线切于点,,即可得到,则或,从而得到,在令,,利用导数求出函数的最小值,即可得解;
【详解】因为,,
所以,,
设公切线与切于点,与曲线切于点,,
所以,
所以,所以,所以或,
因为,所以,所以,
所以,
令,,
则,所以当时,当时,
所以在上单调递减,在上单调递增,
所以,所以实数的最小值为.
故选:A
考点08:与切线有关的最值(范围)问题
39.已知为函数图象上一点,则曲线在点处的切线的倾斜角的最小值为( )
A.B.C.D.0
【答案】A
【分析】由导数的几何意义可求出切线的斜率即为的范围,再根据斜率与倾斜角的关系即可求解.
【详解】因为,即曲线在点处的切线的斜率,
所以倾斜角,即倾斜角的最小值为.
故选:A.
40.若关于的不等式恒成立,则实数的取值范围是( )
A.B.C.D.
【答案】C
【分析】设,,求两个曲线公切线的斜率即可.
【详解】设,,依题意只需求公切线斜率即可.
,,设切点分别为,,
则切线方程为,即.
,即.
则,由①得,
代入②得:,则,
故公切线斜率为或,如图,.
故选:C.
41.已知,若点为曲线:与曲线:的交点,且两条曲线在点处的切线重合,则实数的最大值为( )
A.B.C.D.
【答案】B
【详解】设点的横坐标为,则由可得,,
又可得,,
所以,解得或(舍去),
由点为曲线:与曲线:的交点,
所以与为同一点,
所以,即,
令,
则,
令可得,
由知,当时,,当时,,
所以在上单调递增,在上单调递减,
所以,
故实数的最大值为.
故选:B
42.若曲线有两条过的切线,则的范围是____________.
【答案】
【分析】由题可将曲线有两条过的切线转化为函数图象与直线有两个交点,然后利用导数研究单调性,画出大致图象,即可得答案.
【详解】设切线切点为,,又,所以切线斜率为
因为,所以切线方程为:.
又切线过,则,即
则由题可知函数图象与直线有两个交点,
由得,由得
所以在上单调递增,在上单调递减.
又,又,,,.
据此可得大致图象如下.
则由图可得,当时,曲线有两条过的切线.
故答案为:.
43.若存在直线与曲线都相切,则的取值范围是( )
A.B.C.D.
【答案】D
【分析】先利用导数的几何意义求出两个曲线的公切线,建立方程消参得,构造函数,求导研究函数的单调性求值域,解关于a的一元二次不等式即可.
【详解】设该直线与相切于点,
因为,所以,所以,
所以该切线方程为,即.
设该直线与相切于点,
因为,所以,所以,
所以该切线方程为,即.
所以,
所以,
令,则,
所以当时,,当时,,
所以在和上单调递减;在和上单调递增.
又-1,所以,
所以,解得,
所以的取值范围为.
故选:D.
考点巩固卷21 双曲线方程及其性质(十一大考点)-备战2024年高考数学一轮复习高分突破(新高考通用): 这是一份考点巩固卷21 双曲线方程及其性质(十一大考点)-备战2024年高考数学一轮复习高分突破(新高考通用),文件包含考点巩固卷21双曲线方程及其性质十一大考点原卷版docx、考点巩固卷21双曲线方程及其性质十一大考点解析版docx等2份试卷配套教学资源,其中试卷共68页, 欢迎下载使用。
考点巩固卷20 椭圆方程及其性质(十大考点)-备战2024年高考数学一轮复习高分突破(新高考通用): 这是一份考点巩固卷20 椭圆方程及其性质(十大考点)-备战2024年高考数学一轮复习高分突破(新高考通用),文件包含考点巩固卷20椭圆方程及其性质十大考点原卷版docx、考点巩固卷20椭圆方程及其性质十大考点解析版docx等2份试卷配套教学资源,其中试卷共63页, 欢迎下载使用。
考点巩固卷18 空间向量与立体几何(九大考点)-备战2024年高考数学一轮复习高分突破(新高考通用): 这是一份考点巩固卷18 空间向量与立体几何(九大考点)-备战2024年高考数学一轮复习高分突破(新高考通用),文件包含考点巩固卷18空间向量与立体几何九大考点原卷版docx、考点巩固卷18空间向量与立体几何九大考点解析版docx等2份试卷配套教学资源,其中试卷共76页, 欢迎下载使用。












