2022-2023学年广东省广州市荔湾区高二下学期期末质量检测数学试题（含解析）

这是一份2022-2023学年广东省广州市荔湾区高二下学期期末质量检测数学试题（含解析），共23页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。

1.函数f(x)=x−cs x,f′(x0)=12,x0∈(0,3π2)，则x0等于
( )
A. 4π3B. 7π6C. 2π3D. π6
2.从2,4,6,8中任取3个数字，从1,3,5中任取2个数字，则一共可以组成五位数(没有重复数字)的个数是
( )
A. 720B. 1200C. 1440D. 1728
3.学校乒乓团体比赛采用5场3胜制(5场单打)，每支球队派3名运动员参赛，前3场比赛每名运动员各出场1次，其中第1、2位出场的运动员在后2场比赛中还将各出场1次，假设某球队派甲、乙、丙3名运动员参加比赛，则所有可能的出场情况的种数为
( )
A. 12B. 18C. 30D. 36
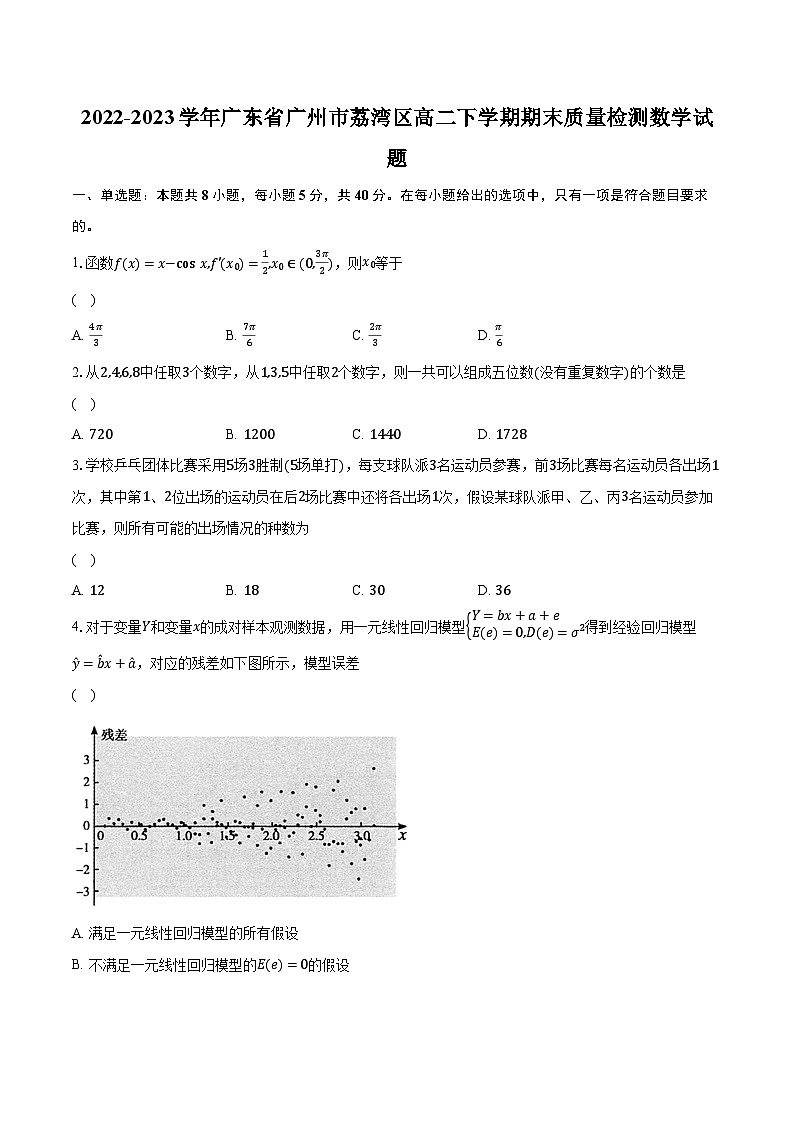
4.对于变量Y和变量x的成对样本观测数据，用一元线性回归模型Y=bx+a+eE(e)=0,D(e)=σ2得到经验回归模型y=bx+a，对应的残差如下图所示，模型误差
( )
A. 满足一元线性回归模型的所有假设
B. 不满足一元线性回归模型的E(e)=0的假设
C. 不满足一元线性回归模型的D(e)=σ2假设
D. 不满足一元线性回归模型的E(e)=0和D(e)=σ2的假设
5.已知函数fx=ax+1xa∈R，且满足f′−1=0，则
( )
A. 函数fx在x=1处有极大值B. 函数fx在区间−1,1上是减函数
C. 函数f′x有两个极值点D. 函数f′x在区间0,+∞上是增函数
6.“杨辉三角”是我国数学史上的一个伟大成就，是二项式系数在三角形中的一种几何排列．如图所示，去除所有为1的项，依此构成数列2,3,3,4,6,4,5,10,10,5,…，则此数列的前45项的和为
( )
A. 2026B. 2025C. 2024D. 2023
7.甲､乙､丙三人相互做传球训练，第1次由甲将球传出，每次传球时，传球者都等可能地将球传给另外两个人中的任何一人，则6次传球后球在甲手中的概率为( )
A. 1132B. 3196C. 516D. 1748
8.已知曲线y=x+ln x在点1,1处的切线与曲线y=ax2+(a+4)x+ln x−1只有一个公共点，则实数a的取值范围是
( )
A. a≥0B. a≥0或a=−1C. −1≤a≤0D. a≥−1
二、多选题：本题共4小题，共20分。在每小题给出的选项中，有多项符合题目要求。
9.已知二项式2 x−1 x6，则
( )
A. 展开式中x2的系数是−192B. 展开式中没有常数项
C. 展开式中各项系数之和为1D. 展开式中二项式系数最大的项是第3项
10.随机抽取7家超市，得到其广告支出x(万元)与销售额y(万元)数据如下，则
( )
A. 销售额与广告支出正相关
B. 销售额与广告支出的变化趋势相同，但广告支出超过10万元后，销售额增加幅度变缓
C. 销售额与广告支出线性相关越强，相关系数r越接近0
D. 要得到销售额的预测值，模型y=22.47+11.58lnx比模型y=1.55x+29.40更可靠
11.猜歌名游戏是根据歌曲的主旋律制成的铃声来猜歌名．某嘉宾参加猜歌名节目，猜对每首歌曲的歌名相互独立，猜对三首歌曲A,B,C歌名的概率及猜对时获得相应的公益基金分别是：猜对歌曲A的概率为0.8，可获公益基金1千元；猜对歌曲B的概率为0.5，可获公益基金2千元；猜对歌曲C的概率为0.5，可获公益基金3千元．规则如下：按照A,B,C的顺序猜，只有猜对当前歌曲的歌名才有资格猜下一首，记嘉宾获得的公益基金总额为X千元，则
( )
A. PX=3=0.4B. E2X+1=5.4
C. D2X+1=18.24D. 获得公益基金的期望值与猜歌顺序无关
12.已知函数f(x)=ex(2x−1)x−1，则
( )
A. 对任意x>1，有fx≥4e32恒成立
B. 当m<0时，函数y=fx−m有2个零点
C. 存在实数k，使得方程fx=kx有3个实数解
D. 若fa=fb(a三、填空题：本题共4小题，每小题5分，共20分。
13.已知随机变量X∼N170,52，则PX≤165等于 .(参考数据：P(μ−σ14.在5道试题中有3道代数题和2道几何题，每次从中随机抽出1道题，抽出的题不再放回．设事件A为“第1次抽到代数题”，事件B为“第2次抽到几何题”，则P(BA)= ．
15.用半径为R的圆形铁皮剪出一个顶点在圆心，圆心角为α的扇形，制成一个圆锥形容器．当该容器的容积最大时，扇形的圆心角α= ．
16.已知函数fx=xx−c2在x=2处有极小值，则c等于 ；若曲线y=fx有3条过点0,a的切线，则实数a的取值范围是 ．
四、解答题：本题共6小题，共70分。解答应写出文字说明，证明过程或演算步骤。
17.(本小题10分)
已知数列an的首项a1=23，且满足an+1=2anan+1．
(1)求数列an的通项公式；
(2)若1a1+1a2+1a3+⋯+1an<100，求满足条件的最大整数n．
18.(本小题12分)
某通信公司为了更好地满足消费者对流量的需求，推出了不同定价的流量包，经过一个月的统计，获取了容量为80万人的样本．同时为了进一步了解年龄因素是否对流量包价格有影响，统计了小于40岁和大于等于40岁两个年龄段人群的购买人数，收集数据整理如表所示．
表1
表2
(1)试根据这些数据建立购买总人数关于定价的经验回归方程，并估计定价为10元/月的流量包的购买人数；
(2)若把50元/月以下(不包括50元)的流量包称为低价流量包，50元/月以上(包括50元)的流量包称为高价流量包，根据以上数据完成列联表，依据α=0.05的独立性检验，判断年龄段和流量包价格是否有关联．附：
b=i=1nxi−xyi−yi=1nxi−x2，a=y−bx，χ2=nad−bc2a+bc+da+cb+d．
19.(本小题12分)
某流水线生产一批A 产品，按质量标准分为一等品､二等品､三等品，共三个等级．现从该批产品中随机抽取100件，其中一等品有80件，二等品有10件，三等品有10件．
(1)若根据产品等级，按分层随机抽样的方法从这100件产品中抽取10件，再从这10件产品中随机抽取3件，记这3件产品中一等品的数量为X，求X的分布列与数学期望；
(2)若将100件产品中各等级的频率视为概率，从流水线上任取5件产品，记这5件产品中一等品的数量为Y，求Y的数学期望与方差．
20.(本小题12分)
如图，在三棱柱ABC−A1B1C1中，点O为线段BC的中点，点E为线段AA1上一动点，AB=AC=AA1=1，∠A1AB=∠A1AC=60∘,AB⊥AC．

(1)若点E为线段AA1中点，求证：OE⊥平面BB1C1C；
(2)求直线BC1与平面EBC所成角的正弦值的最大值．
21.(本小题12分)
已知抛物线C:y2=2pxp>0的焦点为F，点A2,m在抛物线上，且满足AFAO= 32，其中O为坐标原点．
(1)求抛物线C的标准方程；
(2)直线l与抛物线C相交于M、N两点，以MN为直径的圆过点P1,2，作PD⊥MN，D为垂足．是否存在定点Q，使得DQ为定值？若存在，求出点Q的坐标；若不存在，请说明理由．
22.(本小题12分)
已知函数fx=axex−12(x+1)2,a∈R．
(1)讨论函数fx的单调性；
(2)当a>1时，令gx=lnx−12x2−1，求证：fx>gx
答案和解析
1.【答案】B
【解析】【分析】
本题考查基本初等函数的导数公式，属于基础题．
根据导数运算法则求导，然后列出等式，结合x0范围求解即可．
【解答】
解：函数 fx=x−csx ，则 f′x=1+sinx ，
所以 f′x0=1+sinx0=12 ，即 sinx0=−12 ，
又因为 x0∈0,3π2 ，所以 x0=7π6 ．
故选：B．
2.【答案】C
【解析】【分析】
本题考查排列与组合的综合应用，属于基础题．
可先选后排，共有 C43C32A55 种方法，计算即可．
【解答】
解：从 2,4,6,8 中任取3个数字有C43种方法，
从1,3,5中任取2个数字有C32种方法，
再把取出的5个数全排列共有 C43C32A55=1440种，
故一共可以组成1440个没有重复数字的五位数．
故选：C．
3.【答案】C
【解析】【分析】
本题考查简单的排列问题，属于基础题．
对比赛的场数进行分类讨论，确定每种情况下不同的出场情况的种数，结合分类加法计数原理可得结果．
【解答】
解：分以下几种情况讨论：
①若 3 场比赛结束，此时，不同的出场情况种数为 A33=6 种；
②若 4 场比赛结束，则第 4 场为第 1 或第 2 位运动员出场，
此时，不同的出场情况种数为 2A33=12 种；
③若 5 场比赛结束，则第4， 5 场为第 1 和第 2 位运动员各出场 1 次，
此时，不同的出场情况种数为 A22A33=12 种．
综上所述，不同的出场情况种数为 6+12+12=30 种．
故选：C．
4.【答案】C
【解析】【分析】
本题考查一元线性回归模型的有关概念，属于基础题．
根据一元线性回归模型 Y=bx+a+eE(e)=0,D(e)=σ2 有关概念即可判断．
【解答】
解：用一元线性回归模型 Y=bx+a+eE(e)=0,D(e)=σ2 得到经验回归模型 y=bx+a ，根据对应的残差图，残差点比较均匀地分布在x轴两侧，但残差点随着x的增大逐渐偏离x轴，所以模型误差满足一元线性回归模型的E(e)=0 的假设，但不满足 D(e)=σ2 的假设，
故选：C．
5.【答案】D
【解析】【分析】
本题考查利用导数判断已知函数的单调性及极值，属于中档题．
先由 f′−1=0 求出 a ，然后利用导数求出函数的单调区间和极值，再分析判断即可
【解答】
解： fx 的定义域为 (−∞,0)∪(0,+∞) ，
由 fx=ax+1xa∈R ，得 f′x=a−1x2a∈R ，
因为 f′−1=0 ，所以 f′−1=a−1=0 ，得 a=1 ，
所以 fx=x+1x ， f′x=1−1x2=x2−1x2 ，
由 f′x>0 ，得 x<−1 或 x>1 ，由 f′x<0 ，得 −1所以 fx 在 (−∞,−1) 和 (1,+∞) 上递增，在 (−1,0) 和 (0,1) 上递减，
所以 fx 在 x=−1 时取得极大值，在 x=1 时取得极小值，
所以AB错误，
令 gx=f′x=1−1x2 ，则 g′x=2x3 ( x≠0 )，
当 x<0 时， g′x<0 ，当 x>0 时， g′x>0 ，
所以 gx=f′x=1−1x2 在 (−∞,0) 上递减，在 (0,+∞) 上递增，无极值点，
所以C错误，D正确，
故选：D．
6.【答案】A
【解析】【分析】
本题考查杨辉三角，分组(并项)法求和，属于中档题．
根据“杨辉三角”的特点可知 n 次二项式的二项式系数对应“杨辉三角”中的第 n 行，从而得到第 n 行去掉所有为 1 的项的各项之和为： 2n−2 ；根据每一行去掉所有为 1 的项的数字个数成等差数列的特点可求得至第10 行结束，数列共有 45 项，则第 45 项为 C109=10 ，从而求和可得结果．
【解答】
解：由题意可知， n 次二项式的二项式系数对应“杨辉三角”中的第 n 行
则“杨辉三角”第 n 行各项之和为： 2n
∴第 n 行去掉所有为 1 的项的各项之和为： 2n−2
从第2 行开始每一行去掉所有为 1 的项的数字个数为： 1,2,3,4,⋅⋅⋅
则： 1+2+3+4+5+6+7+8+9=45 ，即至第10 行结束，数列共有 45 项
∴第 45 项为第10 行最后 1 个不为 1 的数，即为： C109=10
∴前 45 项的和为： 21−2+22−2+23−2+⋅⋅⋅+210−2=21−2101−2−2×10=2026
故选：A．
7.【答案】A
【解析】【分析】
本题考查全概率公式，等比数列的实际应用，属于中档题．
设 n 次传球后球在甲手中的概率为 pn ，求出 p1=0 ，根据题意求出数列 pn 的递推公式，求出 pn 的表达式，即可求得 p6 的值．
【解答】
解：设 n 次传球后球在甲手中的概率为 pn ，当 n=1 时， p1=0 ，
设 An= “ n 次传球后球在甲手中”，则 An+1=AnAn+1+AnAn+1 ，
则 P(An+1)=P(AnAn+1)+P(AnAn+1)=P(An)P(An+1∣An)+P(An)P(An+1∣An) ．
即 pn+1=pn×0+1−pn×12=121−pn ，
所以， pn+1−13=−12pn−13 ，且 p1−13=−13 ，
所以，数列 pn−13 是以 −13 为首项，以 −12 为公比的等比数列，
所以， pn−13=−13⋅−12n−1 ，所以， pn=131−−12n−1 ，
所以 6 次传球后球在甲手中的概率为 p6=13×1+132=1132 ．
故选：A
8.【答案】B
【解析】【分析】
本题考查利用导数研究公切线问题，属于较难题．
根据导数的几何意义求出曲线 y=x+lnx 的切线方程，要保证切线与曲线 y=ax2+a+4x+lnx−1 只有一个公共点，关键就是转化为 ax2+a+2x+lnx=0 有且只有一正解，从而构造函数，分类讨论，结合导数解决问题．
【解答】
解：由 y=x+lnx 得 y′=1+1x ，则 y′|x=1=2 ，
故曲线 y=x+lnx 在点 1,1 处的切线方程为 y−1=2(x−1) ，即 2x−y−1=0 ，
而切线 2x−y−1=0 与曲线 y=ax2+a+4x+lnx−1 只有一个公共点，
即 2x−1=ax2+a+4x+lnx−1 有且只有一正解，
即 ax2+a+2x+lnx=0 有且只有一正解，
令 g(x)=ax2+a+2x+lnx,(x>0) ，则 g′(x)=2ax+a+2+1x=2ax2+(a+2)x+1x=(2x+1)(ax+1)x ，
由于 x>0 ，故 2x+1>0 ，
当 a=0 时， g′(x)>0 ， g(x) 在 (0,+∞) 上单调递增，
且 g(x)=2x+lnx,(x>0) ， g(1e2)=2e2−2<0,g(1)=2>0 ，
即 g(x) 在 (0,+∞) 上存在唯一零点，即 ax2+a+2x+lnx=0 有且只有一正解；
当 a>0 时， g′(x)>0 ， g(x) 在 (0,+∞) 上单调递增，
由于 ax2+a+2x 的最小值为 −(a+2)24a<0 ，故当 x 趋向于0时， g(x) 可取到负值，
且 g(1)=2a+2>0 ，故 g(x) 在 (0,+∞) 上存在唯一零点，
即 ax2+a+2x+lnx=0 有且只有一正解；
当 a<0 时，当 00 ， g(x) 在 (0,−1a) 上单调递增，
当 x>−1a 时， g′(x)<0 ， g(x) 在 (−1a,+∞) 上单调递减，
故 g(x)max=g(−1a)=−1a−1+ln(−1a) ，
令 h(x)=lnx+x−1,(x>0) ，则 h(x) 在 (0,+∞) 上单调递增，且 h(1)=0 ，
此时要使 ax2+a+2x+lnx=0 有且只有一正解，故需 −1a−1+ln(−1a)=0,∴a=−1 ，
综合以上可知 a≥0 或 a=−1 ，
故选：B．
9.【答案】AC
【解析】【分析】
本题考查二项式定理，属于中档题．
先求得二项式2 x−1 x6的展开式的通项公式Tr+1=C6r26−r−1rx3−r，然后逐项判断．
【解答】
解：二项式2 x−1 x6的展开式的通项公式为Tr+1=C6r2 x6−r⋅−1 xr=C6r26−r−1rx3−r，
令3−r=2，得r=1，则T2=−C6125x2=−192x2，
所以展开式中x2的系数是−192，故A正确；
令3−r=0，得r=3，则T4=−C6323=−160，所以展开式中有常数项，故 B错误；
令x=1，得2 x−1 x6=1，故 C正确；
二项展开式中一共有七项，所以展开式中二项式系数最大的项是中间项即第4项，故D错误；
故选：AC．
10.【答案】ABD
【解析】【分析】
本题考查散点图和样本相关系数，属于中档题．
作出散点图，由散点图可判断ABD选项；根据线性相关系数与线性相关关系的强弱可判断C选项．
【解答】
解：对于A选项，作出散点图如下图所示：

由散点图可知，销售额与广告支出正相关，A对；
对于B选项，由散点图可知，销售额与广告支出的变化趋势相同，
但广告支出超过10万元后，销售额增加幅度变缓，B对；
对于C选项，销售额与广告支出线性相关越强，相关系数r的绝对值越接近1，C错；
对于D选项，由散点图可知，整体上y随着x的增大而增大，当x≥10时，销售额y增加幅度变缓，
所以，要得到销售额的预测值，模型y=22.47+11.58lnx比模型y=1.55x+29.40更可靠，D对．
故选：ABD．
11.【答案】BC
【解析】【分析】
本题考查离散型随机变量的期望和方差，属于中档题．
确定X的取值，求得每个值对应概率，可判断A；继而可求得期望和方差，根据期望和方差的性质可判断B，C；再求出按照A,C,B的顺序猜时的期望值，比较可判断D．
【解答】
解：由题意，可分别用A,B,C表示猜对三首歌曲A,B,C歌名的的事件，
则A,B,C相互独立，
按照A,B,C的顺序猜，则X的取值可能为0,1,3,6，
则PX=0=PA=0.2，PX=1=PAB=0.8×0.5=0.40，
P(X=3)=P(ABC)=0.8×0.5×0.5=0.2，
P(X=6)=P(ABC)=0.8×0.5×0.5=0.2，
则EX=0×0.2+1×0.4+3×0.2+6×0.2=2.2，
D(X)=(0−2.2)2×0.2+(1−2.2)2×0.4+(3−2.2)2×0.2+(6−2.2)2×0.2=4.56，
故E2X+1=2×2.2+1=5.4，D2X+1=4×4.56=18.24，
由此可知A错误；B正确，C正确；
假设按照A,C,B的顺序猜，设Y表示此时获得的公益基金总额
则PY=0=PA=0.2，PY=1=PAC=0.8×0.5=0.40，
P(Y=4)=P(ACB)=0.8×0.5×0.5=0.2，P(Y=6)=P(ABC)=0.8×0.5×0.5=0.2，
则EY=0×0.2+1×0.4+4×0.2+6×0.2=2.4，
与按照A,B,C的顺序猜的期望值不同，故 D错误，
故选：BC．
12.【答案】ACD
【解析】【分析】
本题综合考查导数的应用，涉及面较广，难度较大，解答时要注意判断函数值情况，并利用导数判断函数的单调性，从而作出函数图象，数形结合，解决问题．
判断函数值情况，利用导数判断函数单调性，作出函数图象，由此可判断A，B；数形结合，判断C；构造函数g(x)=f(x)−f(−x),(0【解答】
解：由fx=ex2x−1x−1可知定义域为{x|x≠1),
当x<12或x>1时，fx>0；当12又f′(x)=ex⋅2x−1x−1+ex⋅2(x−1)−(2x−1)(x−1)2=ex[2x−1x−1−1(x−1)2]=x(2x−3)ex(x−1)2，
令f′(x)>0，则x<0或x>32，令f​′(x)<0，则0即f(x)在(−∞,0),(32,+∞)上单调递增，在(0,1),(1,32)上单调递减，
故f(x)在x=0时取极大值f0=1，在x=32时取极小值f32=4e32；
当x从1的左侧趋近于1时，f(x)趋近于负无穷，当x从1的右侧趋近于1时，f(x)趋近于正无穷，当x→+∞时，f(x)增加的幅度越来越块，即图像较陡，
由此可作出函数f(x)的图象如图：

由图象可知，对任意x>1，有fx≥f32=4e32恒成立， A正确；
当m<0时，直线y=m与f(x)的图象将会有一个交点，
即函数y=fx−m有1个零点，B错误；
由图象，设l为f(x)的过原点且和x>1的部分图象相切的切线，斜率设为kl，
当直线y=kx的斜率k>kl时，即存在直线与f(x)的图象有3个交点，
即存在实数k，使得方程fx=kx有3个实数解，C正确；
由fa=fb(a设g(x)=f(x)−f(−x),(0故g(x)=f(x)−f(−x),(0即g(x)由于f(x)在(−∞,0)上单调递增，故a<−b,∴a+b<0， D正确，
故选：ACD．
13.【答案】0.15865
【解析】【分析】
本题考查正态分布，属于基础题．
根据正态分布的对称性，以及已知区间的概率，即可求得答案．
【解答】
解：由题意随机变量 X∼N170,52 ，
则 P165故 P(X⩽165)=12[1−P(165故答案为：0.15865
14.【答案】12
【解析】【分析】
本题考查条件概率的概念与计算，属于基础题．
先求得 P(A),P(AB) ，结合条件概率的计算公式，即可求解．
【解答】
解：由题意得， P(A)=35 ， P(AB)=35×24=310 ，
所以在第1次抽到代数题的条件下，第2次抽到几何题的概率为：
PB∣A=PABPA=31035=12 ．
15.【答案】2 63π
【解析】【分析】
本题考查导数在实际问题中的应用，圆锥的体积，属于中档题．
设圆锥底面半径为 r ，高为 h ，那么 V=13πr2h ，再根据 r2=R2−h2 ，代入得到 V=13πR2−h2h ，利用导数求得函数取最大值时， h 与R的关系 ，可得圆心角 α ．
【解答】
解：设圆锥的底面半径为 r ，高为 h ，容积为 V ，
可得r2+h2=R2 ，
因此 V=13πr2h=13πR2−h2h=−13πh3+13πR2h(0变量为h，则V′=−πh2+13πR2 ，令 V′=0 ，解得 h= 33R ，
当 00 ，
当 R>h> 33R 时， V′<0 ，
所以当 h= 33R 时容积最大，
把 h= 33R 代入 r2+h2=R2 ，得 r= 63R，
由 Rα=2πr ，得 α=2 63π ，
即圆心角为 α=2 63π 时容积最大，
故答案为： 2 63π．
16.【答案】2；0,6427
【解析】【分析】
本题考查利用导数根据极值点求参和已知切线求参数，属于较难题．
利用导数分析函数 fx 的单调性，分析可知 c>0 ，根据函数 fx 的极小值点可求得 c 的值；设切点为 t,tt−22 ，利用导数写出切线方程，将点 0,a 的坐标代入切线方程，可知方程 a=4t2−2t3 有三个不等的实根，设 gt=4t2−2t3 ，利用导数分析函数 gt 的单调性与极值，分析可知函数 y=a 与函数 gt 的图象有三个公共点，数形结合可得出实数 a 的取值范围．
【解答】
解：因为 fx=xx−c2 ，则 f′x=x−c2+2xx−c=x−c3x−c ，
由 f′x=0 可得 x=c 或 x=c3 ，且 c 与 c3 同号，
因为函数 fx=xx−c2 在 x=2 处有极小值，即函数 fx 的极小值点为正数，
则必有 c>0 ，此时， c3所以，函数 fx 的极小值点为 x=c ，故 c=2 ，则 fx=xx−22 ，
设切点为 t,tt−22 ，因为 f′x=x−23x−2 ，则 f′t=t−23t−2 ，
所以，切线方程为 y−tt−22=t−23t−2x−t ，
将点 0,a 的坐标代入切线方程可得 a=tt−22−tt−23t−2=4t2−2t3 ，
令 gt=4t2−2t3 ，则 g′t=8t−6t2 ，令 g′t=0 ，可得 t=0 或 t=43 ，列表如下：
由题意可知，函数 y=a 与函数 gt 的图象有三个公共点，如下图所示：

由图可知，当 0因此，实数 a 的取值范围是 0,6427 ．
故答案为： 2 ； 0,6427 ．
17.【答案】解：(1)因为 an+1=2anan+1 ， a1=23 ，
所以易知 an≠0 ，
取倒数得， 1an+1=an+12an=12+12an ，
即 1an+1−1=121an−1 ，
因为 a1=23 ，所以 1a1−1=12 ，
所以 1an−1≠0 ，
所以 1an+1−11an−1=12 为常数，
所以 1an−1 是以 12 为首项， 12 为公比的等比数列；
所以 1an−1=12n ，则 1an=12n+1 ，
所以 an=112n+1=2n2n+1 ，
即数列 an 的通项公式为 an=2n2n+1 ．
(2)因为 1an=12n+1 ，
所以 1a1+1a2+⋯+1an=n+121−12n1−12=n+1−12n ，
令 bn=n+1−12n ，
显然， bn 单调递增， bn=n+1−12n<100
因为 b99=100−1299<100 ， b100=101−12100>100 ，
所以 n≤99 ，
所以满足条件的最大整数n为 99 ．

【解析】本题考查等比数列的通项公式和前n项和公式，求数列的通项公式，数列的单调性，属于中档题．
(1)由已知得 1an+1−1=121an−1 ，再由等比数列的定义可得答案；
(2)由(1)求出 1an=12n+1 ，再由等比数列的求和公式可得 1a1+1a2+⋯+1an=n+1−12n ，令 bn=n+1−12n ，根据 bn 的单调性可得答案．
18.【答案】解：(1)由表格中的数据可得 x=20+30+50+604=40 ， y=30+27+13+104=20 ，
b=(20−40)×(30−20)+(30−40)×(27−20)+(50−40)×(13−20)+(60−40)×(10−20)(20−40)2+(30−40)2+(50−40)2+(60−40)2
=−0.54 ， a=y−bx=20+0.54×40=41.6 ，
所以， y 关于 x 的经验回归方程为 y=−0.54x+41.6 ，
当 x=10 时， y=−5.4+41.6=36.2 (万人)，
因此，估计定价为 10 元/月的流量包的购买人数为 36.2 万人．
(2)零假设 H0: 年龄段和流量包价格没有关联，
由题中数据完善 2×2 列联表如下表所示：
χ2=80×25×8−32×15240×40×57×23≈2.990<3.841=x0.05 ，
所以，依据小概率 α=0.05 的独立性检验，我们推断 H0 成立，
即认为年龄段和流量包价格没有关联．

【解析】本题考查经验回归方程，独立性检验，属于中档题．
(1)计算出 x 、 y 的值，将表格中的数据代入公式，求出 b 、 a 的值，可得出经验回归方程，将 x=10 代入经验回归方程，可得所求结果；
(2)完善 2×2 列联表，计算出 χ2 值，结合临界值表可得出结论．
19.【答案】解：(1)由题意可知抽取的10件产品中一等品有 8080+10+10×10=8 件，二等品有 1080+10+10×10=1 件，三等品有 1080+10+10×10=1 件，
所以 X 的可能取值为1，2，3，则
P(X=1)=C81C22C103=115 ，P(X=2)=C82C21C103=715 ，P(X=3)=C83C103=715 ，
所以 X 的分布列如下
所以 E(X)=1×115+2×715+3×715=125
(2)由题意得从这100件产品中取出1件是一等品的概率为 80100=45 ，
则由题意可知 Y∼B5,45 ，
所以 E(Y)=5×45=4,D(Y)=5×45×1−45=45

【解析】本题考查超几何分布的分布列和均值，二项分布的均值和方差，属于中档题．
(1)先根据分层随机抽样的定义，按比例求出所抽的10件产品中一等品､二等品､三等品的件数分别为8，1，1件，则 X 的可能取值为1，2，3，然后求出相应的概率，从而可求出 X 的分布列与数学期望；
(2)先求出取出是一等品的概率，则由题意可知 Y 服从二项分布，然后利用二项分布的期望和方差公式可求出 Y 的数学期望与方差．
20.【答案】解：(1)因为点 E 为线段 AA1 中点，故 AE=12AA1=12 ，
而 ∠A1AB=60∘ ，故 BE2=AE2+AB2−2AE×ABcs∠A1AB
=14+1−2×12×1×12=34 ，
故 BE= 32 ，则 AE2+BE2=(12)2+( 32)2=1=AB2 ，
则 BE⊥AE,∴BE⊥AA1 ，同理可得 CE= 32 ， CE⊥AA1 ，
又CE∩BE=E,CE,BE⊂ 平面 BEC ，故 AA1⊥ 平面 BEC ，
而OE⊂ 平面 BEC ，故 AA1⊥OE ，而 AA1//BB1,∴BB1⊥OE ；
由 BE= 32 ， CE= 32 ，得 BE=CE ，又点 O 为线段 BC 的中点，故 OE⊥BC ，
由 BB1∩BC=B,BB1,BC⊂ 平面 BB1C1C ，故 OE⊥ 平面 BB1C1C ．
(2)由(1)可知当点 E 为线段 AA1 中点时， AA1⊥ 平面 BEC ，又 AA1//BB1 ，
故 BB1⊥ 平面 BEC ，而 BC⊂ 平面 BEC ，则 BB1⊥BC ，
由于 AA1 的中点始终是存在的，故 BB1⊥BC 一定成立，故四边形 BCC1B1 为矩形，
如图，连接 EC1,BC1 ，

由(1)知OE⊥BC ，
由于 AB⊥AC ，故 BC= AB2+AC2= 2 ；
当E为 AA1 中点时，
结合(1)求得 AA1 到平面 BCC1B1 的距离为 ( 32)2−( 22)2=12 ，
设 C1 到平面 BEC 的距离为d，则 VC1−BEC=VE−BCC1=13×12× 2×1×12= 212 ，
即 13×S▵BEC×d= 212,∴13×12× 2×OE×d= 212 ，即 OE×d=12 ，
由于点 E 为线段 AA1 上一动点，故当 E 为线段 AA1 中点时，
即 OE⊥ 平面 BB1C1C 时， OE 最小为 12 ，此时d取最大值1，
故直线 BC1 与平面 EBC 所成角的正弦值的最大值为 dBC1=1 ( 2)2+12= 33 ．

【解析】本题考查线面垂直的判定，线面角的求解，属于较难题．
(1)利用线面垂直的判定定理即可证明结论；
(2)由题意说明四边形 BCC1B1 为矩形，由此根据三棱锥的等体积法可求出 C1 到平面 BEC 的距离的最大值，根据线面角的含义即可求得答案．
21.【答案】解：(1)抛物线 C 的准线方程为 x=−p2 ，由抛物线的定义可得 AF=2+p2 ，
将点 A 的坐标代入抛物线方程可得 m2=4p ，
所以， AO= 4+m2= 4+4p=2 1+p ，
所以， AFAO=2+p22 1+p= 32 ，因为 p>0 ，解得 p=2 ，
因此，抛物线 C 的标准方程为 y2=4x ．
(2)若直线 MN⊥y 轴，则直线 MN 与抛物线 C 只有一个公共点，不合乎题意，
设直线 MN 的方程为 x=ty+n ，设点 Mx1,y1 、Nx2,y2 ，
联立 x=ty+ny2=4x，可得 y2−4ty−4n=0， Δ=16t2+16n>0，则 n>−t2 ，
由韦达定理可得 y1+y2=4t， y1y2=−4n ，
PM=x1−1,y1−2=y12−44,y1−2 ， PN=x2−1,y2−2=y22−44,y2−2 ，
因为以 MN 为直径的圆过点 P1,2 ，则 PM⋅PN=0 ，
所以， 116y12−4y22−4+y1−2y2−2=0 ，
显然 y1≠2 且 y2≠2 ，所以， y1+2y2+2+16=0 ，
即 y1y2+2y1+y2+20=0 ，即 −4n+8t+20=0 ，可得 n=2t+5 ，
所以，直线 MN 的方程为 x=ty+2t+5=ty+2+5 ，
由 y+2=0 可得 y=−2 ， x=5 ，所以，直线 MN 过定点 E5,−2 ，
所以， |PE|= (1−5)2+(2+2)2=4 2 ，
因为 PD⊥MN ，当点 Q 为线段 PE 的中点时，即当点 Q 的坐标为 3,0 时，
DQ=12PE=2 2 为定值．
因此，存在定点 Q ，且当点 Q 的坐标为 3,0 时， DQ 为定值．

【解析】本题考查抛物线的方程，抛物线中的定点，定值问题，属于较难题．
(1)利用抛物线的定义结合两点间的距离公式可得出关于 p 的方程，解出 p 的值，即可得出抛物线 C 的标准方程；
(2)分析可知，直线 MN 不与 y 轴垂直，设直线 MN 的方程为 x=ty+n ，设点 Mx1,y1 、 Nx2,y2 ，将直线 MN 的方程与抛物线 C 的方程联立，利用韦达定理，根据已知条件得出 PM⋅PN=0 ，利用平面向量数量积的坐标运算可得出 n 、 t 所满足的关系式，求出直线 MN 所过定点 E 的坐标，利用直角三角形的几何性质可得出定点 Q 的坐标．
22.【答案】解：(1)由题意可知 fx 的定义域为 R ，
f′x=aex+axex−x+1=x+1aex−1 ，
当 a≤0 时， aex−1<0 ，
所以当 x>−1 时， f′x<0 ， fx 单调递减，当 x<−1 时， f′x>0 ， fx 单调递增；
当 a>0 时，令 f′x=0 ，解得 x1=−1 ， x2=−lna ，
①当 −lna=−1 ，即 a=e 时，
f′x≥0 恒成立，所以 fx 在 R 上单调递增，
②当 −lna<−1 ，即 a>e 时，
当 −lna−1 时， f′x>0 ， fx 单调递增，
③当 −lna>−1 ，即 0当 −1−lna 时， f′x>0 ， fx 单调递增，
综上所述，
当 a≤0 时， fx 在 −∞,−1 上单调递增，在 −1,+∞ 上单调递减，
当 a=e 时， fx 在 R 上单调递增，
当 a>e 时， fx 在 −∞,−lna ， −1,+∞ 上单调递增，在 −lna,−1 上单调递减，
当 0(2)令 H(x)=f(x)−g(x)=axex−12(x+1)2−ln x+12(x2−1)=axex−x−1−ln x ， x>0 ，
则 H′(x)=aex+axex−1−1x=(x+1)(axex−1)x ，
令 hx=axex−1 ， x>0 ，
因为 a>1 ，所以 h′x=aex+axex=aexx+1>0 恒成立， hx 单调递增，
又因为 h0=−1<0 ， h1=ae−1>0 ，所以存在 x=t∈0,1 使得 ht=0 ，
所以当 x∈0,t 时， hx<0 ，进而可得 H′x<0 ， Hx 单调递减，
当 x∈t,+∞ 时， hx>0 ，进而可得 H′x>0 ， Hx 单调递增，
因为 a>1 且 ht=atet−1=0 ，即 atet=1 ，
所以两边取对数可得 lnatet=lna+lnt+lnet=0 ，即 lnt+t=−lna<0 ，
所以 Hxmin=Ht=atet−t−1−lnt=atet−1−t+lnt>0 ，
所以 Hx>0 恒成立，即 fx>gx ．

【解析】本题考查导数的综合应用，属于难题．
(1)求导，导论 a 的范围，通过导函数的正负判断函数的单调性；
(2)构造函数 Hx=fx−gx ，探讨函数 Hx 在区间 0,+∞ 上的最小值即可．
超市
A
B
C
D
E
F
G
广告支出x(万元)
1
2
4
6
10
14
20
销售额y(万元)
19
32
44
40
52
53
54
定价x(元/月)
20
30
50
60
<40岁(万人)
10
15
7
8
≥40岁(万人)
20
12
6
2
购买总人数y(万人)
30
27
13
10
年龄段
流量包
合计
<50元
≥50元
<40岁
≥40岁
合计
α
0.1
0.05
0.01
0.005
0.001
xα
2.706
3.841
6.635
7.879
10.828
x
−∞,c3
c3
c3,c
c
c,+∞
f′x
+
0
−
0
+
fx
增
极大值
减
极小值
减
t
−∞,0
0
0,43
43
43,+∞
g′t
−
0
+
0
−
gt
减
极小值 0
增
极大值 6427
减
年龄段
流量包
合计
<50 元
≥50 元
<40 岁
25
15
40
≥40 岁
32
8
40
合计
57
23
80
X
1
2
3
P
115
715
715