2024届福建省优质校高三上学期12月阶段性检测数学试题含答案

这是一份2024届福建省优质校高三上学期12月阶段性检测数学试题含答案，共24页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
一、单选题
1．复数z1，z2在复平面内对应的点分别为（1，2），（0，-1），则z1z2＝（ ）
A．1+iB．2-iC．-2iD．-2-i
【答案】B
【分析】首先根据复数的几何意义求复数，再根据复数的乘法公式求解.
【详解】由复数的几何意义可知，，，
则.
故选：B
2．若集合，且，则集合可以是（ ）
A．B．C．D．
【答案】D
【解析】由得，由此可得答案．
【详解】解：∵，
∴，
又，
∴只有D选项符合，
故选：D．
3．双曲线E经过点，其渐近线方程为，则E的方程为（ ）
A．B．C．D．
【答案】D
【解析】由渐近线方程为，可设所求的双曲线方程为，由双曲线经过点代入可得，从而可得所求的双曲线方程
【详解】解：已知双曲线渐近线方程为，
故可设所求的双曲线方程为，
双曲线经过点，代入可得，
故所求的双曲线方程为.
故选：D.
【点睛】本题主要考查了双曲线的方程的求解，解题的关键是需要由题意设出双曲线的方程，在双曲线的方程求解中，若已知双曲线方程，可得渐近线方程为；但若渐近线方程为程程为可设双曲线方程为．
4．若，，则“”的一个充要条件是（ ）
A．B．
C．D．
【答案】B
【分析】根据命题的定义，可利用赋值对A、C、D三个选项进行验证；利用不等式的性质可得B成立.
【详解】，，
对于A，当时，取，，则，
所以不成立，必要性不成立，故A错误；
对于B，当时，，
由不等式的性质可知，必要性成立；
当时，两边平方，得，即，充分性也成立，故B正确；
对于C，当时，取，，则，
所以不成立，必要性不成立，故C错误；
对于D，当时，取，，则，所以不成立，充分性不成立，故D错误.
故选：B.
5．已知圆，直线过，若被圆所截得的弦长最小值为2，则（ ）
A．B．C．D．
【答案】B
【分析】首先分析题意，利用圆基本定义与直线关系，又可知，M必在圆O的内部，故可知O到直线l的最大距离.
【详解】易知，直线l与y轴交点的坐标为，圆C的圆心坐标为,半径为2.记由题意可知点M必在圆O的内部，且直线l被圆C所截得的弦长的最小值为2时，O到直线l的最大距离为，则.
故选：B
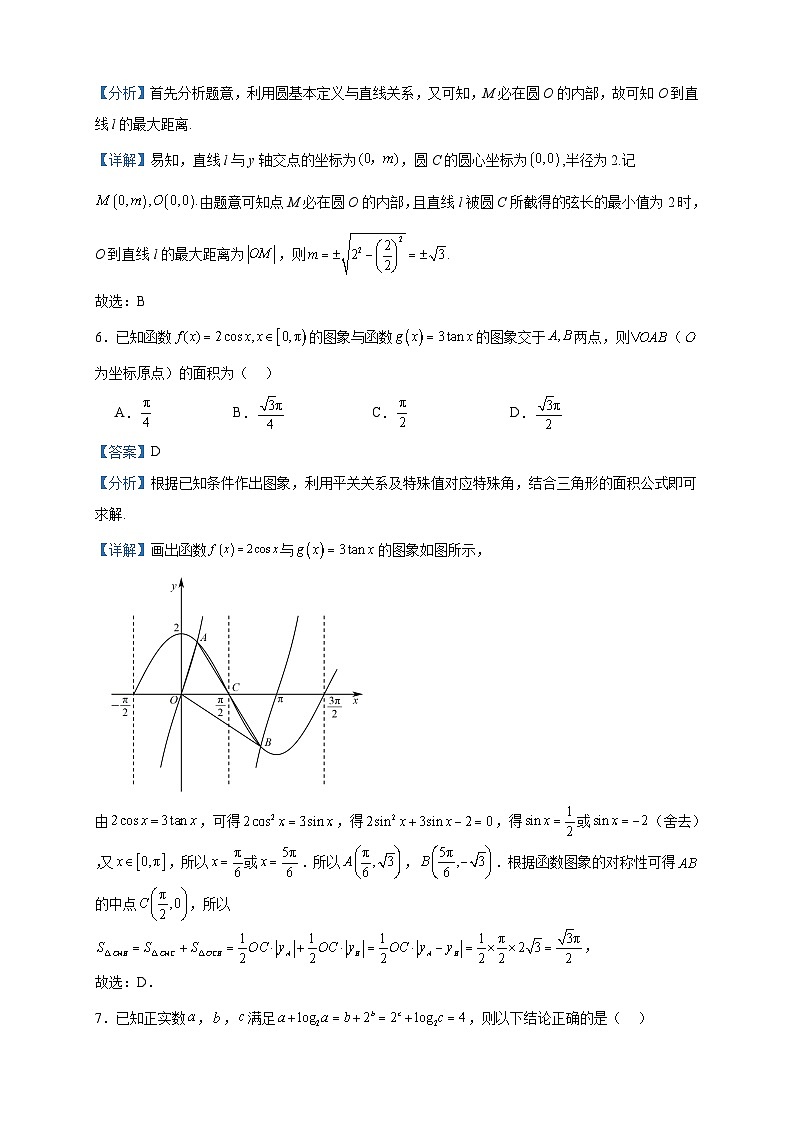
6．已知函数的图象与函数的图象交于两点，则（为坐标原点）的面积为（ ）
A．B．C．D．
【答案】D
【分析】根据已知条件作出图象，利用平关关系及特殊值对应特殊角，结合三角形的面积公式即可求解.
【详解】画出函数与的图象如图所示，
由，可得，得，得或（舍去），又，所以或．所以，．根据函数图象的对称性可得的中点，所以
，
故选：D．
7．已知正实数，，满足，则以下结论正确的是（ ）
A．B．C．D．
【答案】C
【分析】利用指数、对数函数的性质与函数图像进行判断即可.
【详解】令，可知在单调递增，
由，
得所以，
由题，，，
令则，所以有，
在平面直角坐标系中分别作出，，，，
由图像可得，则A错误；
对于B，则，即，
由图像可知，所以，B错误；
对于C，，即，因为，
所以，则，故C正确；
对于D，因为，
即且，所以，D错误；
故选：C
8．已知圆锥的顶点为，母线长为2，底面半径为，点在底面圆周上，当四棱锥体积最大时，
A．B．C．D．
【答案】C
【分析】设圆锥的高为，相交于点，，求得的最大值，以及根据锥体的体积公式，求得 ，令，令导数求解函数的单调性与最值，进而可求解答案.
【详解】设圆锥的高为，相交于点，，则，，，
当且仅当，时，取得最大值，
则
令，则，令，解得
所以在上单调递减，在上单调递增
所以，则四棱锥的体积的最大值为，
所以当四棱锥体积最大时，.
【点睛】本题主要考查了组合体的性质，以及利用导数研究函数的单调性与最值的应用，其中解答中根据结合体的结构特征，求得几何体的体积，再利用导数求解函数的单调性与最值是解答本题的关键，试题有一定的综合性，属于中档试题，着重考查了分析问题和解答问题的能力.
二、多选题
9．下列各组向量中，可以作为所有平面向量的一个基底的是（ ）
A．，B．，
C．，D．，
【答案】ACD
【分析】利用平面向量的共线定理及基底的概念一一判定选项即可.
【详解】易知能作为基底的两个平面向量不能共线，
因为，，，
则选项A、C、D中两个向量均不共线，而B项中，则B错误.
故选：ACD
10．如图，点A，，，，为正方体的顶点或所在棱的中点，则直线平面的是（ ）
A．B．
C． D．
【答案】BC
【分析】利用空间向量、正方体的特征及线面平行的判定定理、面面平行的性质定理一一判定选项即可.
【详解】对于A项，如图所示建立空间直角坐标系，设正方体棱长为2，
则，
所以,
设平面的一个法向量为，则，
令，即，
显然，即与不垂直，故直线与平面不平行，故A错误；

对于B项，如图所示取侧棱中点D，连接AD，BD，由正方体的特征可知，
所以平面即平面，平面，平面，
所以直线平面，故B正确；

对于C项，由正方体的特征易知平面侧面，侧面，
所以直线平面，故C正确；
对于D项，如图所示取正方体一棱中点G，连接，
由正方体的特征可知：，
易知六点共面，故D错误.

故选：BC
11．筒车是我国古代发明的一种灌溉工具，因其经济又环保，至今还在农业生产中得到使用.明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理（如图）.现有一个半径为3米的简车按逆时针方向每分钟旋转1圈，筒车的轴心距离水面的高度为2米.设筒车上的某个盛水筒P到水面的距离为d（单位：米）（在水面下则为负数），若以盛水筒刚浮出水面开始计算时间，设时间为t（单位：秒），已知，则（ ）
A．，其中，且
B．，其中，且
C．大约经过38秒，盛水筒P再次进入水中
D．大约经过22秒，盛水筒P到达最高点
【答案】ABD
【分析】若为筒车的轴心的位置，为水面，为筒车经过秒后的位置，由题设知筒车的角速度，令，易得，而、，即可求的解析式判断A、B的正误，、代入函数解析式求，即可判断C、D的正误.
【详解】由题意知，如图，若为筒车的轴心的位置，为水面，为筒车经过秒后的位置，
筒车的角速度，令且，
∴，故，而，
∴，其中，且，
又
，
若，且，所以，
此时
，
故，其中，且，故A、B正确；
当时，，且，，
∴，
故盛水筒没有进入水中，C错误；
当时，，且，，
故盛水筒到达最高点，D正确.
故选：ABD
12．已知曲线，则（ ）
A．曲线关于直线轴对称
B．曲线与直线有唯一公共点
C．曲线与直线没有公共点
D．曲线上任意一点到原点的距离的最大值为
【答案】ABD
【分析】A只需判断对于任意、是否都有成立即可；B联立直线与曲线求交点即可判断；C联立直线与曲线得，构造，利用导数研究其在上零点个数即可；D令曲线上任意一点且，且到原点距离为，代入曲线方程得，应用换元法、三角恒等变换求最大值.
【详解】对A，将、代入有都成立，即曲线关于直线轴对称，A对；
对B，将代入曲线，整理得，
所以，即曲线与直线有唯一公共点，B对；
对C，将代入曲线，整理得，
令，则，且，
所以在上，递增，上，递减，
又，，而，
所以在上有两个零点，C错；
对D，令曲线上任意一点且，且到原点距离为，
所以，则，
若，则，
所以，
令且，则，即上单调递减，
所以在上单调递增，故，D对.
故选：ABD
【点睛】关键点点睛：C转化为研究函数在上的零点个数问题；D设任意点的极坐标，应用换元法、三角恒等变换、导数研究的最值.
三、填空题
13．的展开式中的系数是 ．（用数字作答）
【答案】
【分析】首先分析出存在有两项，然后分别求出这两项系数，相加即可.
【详解】根据题意,的项在的展开式中有两项，
分别为：和，即和，
则的系数为：.
故答案为：.
14．已知甲、乙两人三分球投篮命中率分别为0.4和0.5，则他们各投两个三分球，至少有一人两球都投中的概率为 ．
【答案】0.37/
【分析】采取正难则反的原则，求出其对立事件，即二人两球都没有投中的概率，再根据对立事件的概率公式求解即可．
【详解】设甲两个三分球都投中的事件为，乙两个三分球都投中的事件为，至少有一人两球都投中的事件为，
则，，，，
由题可知事件与事件互相独立，
所以
,
所以至少有一人两球都投中的概率为，
故答案为：
15．如图中的三角形称为谢尔宾斯基三角形.每个图都是取前一个图中的每个黑色三角形三边的中点将其分成四个小三角形，并将中间三角形变为白色，白色三角形不变.若第一个三角形的面积为1，第个图中白色部分的面积记为，则 .
【答案】
【分析】先计算黑色三角形面积再计算白色部分即可.
【详解】观察可知每个图形中黑色三角形的面积一致，
假设第个图中黑色三角形的面积为，则，
显然是等比数列，公比为，即，
所以.
故答案为：
16．椭圆的左右焦点分别为，E上存在两点A、B满足，，则E的离心率为 .
【答案】
【分析】作点B关于原点的对称点C，连接，推导出三点共线，利用椭圆的定义可求得，推导出，利用勾股定理可得出关于a、c的齐次等式，即可求得该椭圆的离心率．
【详解】作点B关于原点的对称点C，连接，
则O为BC、的中点，故四边形为平行四边形，故且，则，所以，，故A、、C三点共线，
由椭圆定义，，有，所以，则，
再由椭圆定义，有，
因为，所以，
在中，即，所以．
故答案为：．
四、解答题
17．在①；②；③，这三个条件中任选一个，补充在下面问题中，并解答下面问题.问题：在中，内角的对边分别是，，，______.
(1)判断的形状；
(2)点为所在平面内一点，且点与点位于直线的异侧，，，，，求四边形的面积.
注：如果选择多个条件分别解答，按第一个解答计分.
【答案】(1)直角三角形；
(2).
【分析】（1）若选择①、②，利用三角恒等变换及正弦定理计算即可；若选择③，利用正余弦定理计算即可；
（2）根据条件及正余弦定理建立的方程组计算即可.
【详解】（1）若选择①，由，
由正弦定理及二倍角公式可知，
在中，
，
则，而，故，
所以是直角三角形；
若选择②，根据正弦定理
在中，，
所以，
而，故，
所以是直角三角形；
若选择③，由余弦定理可知，
由正弦定理可知，
在中，，
而，故，
所以是直角三角形；
（2）
根据条件及（1）易知，
由余弦定理可知：，
又
，
由，
解方程得，
所以四边形的面积.
18．如图，四边形为矩形，平面平面，是中点，是中点，点在线段上，且.
(1)求证：平面；
(2)若，，求与平面所成角的正弦值.
【答案】(1)证明见解析
(2)
【分析】（1）取的中点，在上取点使，证明四边形是平行四边形， ，从而平面；
（2）由四边形为矩形，平面平面，得平面，设，建立空间直角坐标系，利用，将与平面所成角转化为与平面所成角，即可求解.
【详解】（1）取的中点，在上取点使，连接、、，

，
且，
是中点，是中点，
且，
且，
四边形是平行四边形，，
平面，平面，
平面；
（2）四边形为矩形，，
平面平面，平面平面，平面，
平面，
以为原点，分别以、为轴、轴，平面内过点垂直于的直线为轴，建立如图所示的空间直角坐标系，

，，设，
，，，，，，，
，，
由（1）知且，，
设向量为平面的一个法向量，
则取，则，，得，
，
与平面所成角的正弦值为.
19．已知函数，.
(1)讨论的单调性；
(2)若，求证：当时，.
【答案】(1)见解析
(2)见解析
【分析】（1）依题意，的定义域为，，分类讨论可求的单调性；
（2）当时，要证明，即证，
只需证明. 设，利用导数研究其性质，即可证明
【详解】（1）依题意，的定义域为，，
①当时，，在单调递减；
②当时，当时，；当时，；
所以在单调递减，在单调递增；
③当时，当时，；当时，；
所以在单调递增，在单调递减；
综上，当时，在单调递减；
当时，在单调递减，在单调递增；
当时，在单调递增，在单调递减.
（2）当时，要证明，
即证明，
因为，所以只需证明，
只需证明.
设，
则，
设，则，
所以当时，；当时，；
所以在单调递减，在单调递增；
所以，
所以当时，；当时，；
所以在单调递减，在单调递增；
所以，
所以当时，.
【点睛】本小题考查导数与函数的单调性、不等式等基础知识；考查运算求解能力，推理论证能力；考查函数与方程思想，化归与转化思想，分类与整合思想等．
20．已知数列的前项和为，，，.
(1)是否存在实数，使得数列为等比数列？若存在，求出的值；若不存在，说明理由；
(2)记数列的前项和为，当时，求证：.
【答案】(1)时，数列为等比数列；
(2)证明过程见解析
【分析】（1）根据得到，当和时，不合要求，故求出时，数列为等比数列；
（2）得到为首项为2，公比为2的等比数列，求出，设，利用错位相减法得到.
【详解】（1）①，当时，②，
两式相减得，即，
当时，，不能使得数列为等比数列，舍去，
当时，，
当时，，不能使得数列为等比数列，舍去，
当时，数列为等比数列；
（2）当时，，
故为首项为2，公比为2的等比数列，
故，
则，
故，
令，
则，
两式相减得，
故，.
21．在一个典型的数字通信系统中，由信源发出携带着一定信息量的消息，转换成适合在信道中传输的信号，通过信道传送到接收端.有干扰无记忆信道是实际应用中常见的信道，信道中存在干扰，从而造成传输的信息失真.在有干扰无记忆信道中，信道输入和输出是两个取值的随机变量，分别记作和.条件概率，描述了输入信号和输出信号之间统计依赖关系，反映了信道的统计特性.随机变量的平均信息量定义为：.当时，信道疑义度定义为
(1)设有一非均匀的骰子，若其任一面出现的概率与该面上的点数成正比，试求扔一次骰子向上的面出现的点数的平均信息量；
(2)设某信道的输入变量与输出变量均取值0，1.满足：.试回答以下问题：
①求的值；
②求该信道的信道疑义度的最大值.
【答案】(1)2.40
(2)①；②1
【分析】（1）充分理解题意，利用随机变量的平均信息量定义解决本小题；
（2）由全概率和条件概率公式解决本小题.
【详解】（1）设表示扔一非均匀股子点数，则
扔一次平均得到的信息量为
.
（2）①由全概率公式，得
②由题意，.
所以，
;
其中.
令
.
时时，,
.
22．已知点，动圆过点且与轴相切，是圆的直径，动点的轨迹为曲线.
(1)求的方程；
(2)直线与交于另一点，以线段为直径作圆，已知直线是异于轴且与圆、圆均相切的一条直线，与交于两点，若直线上一点满足交轴于点，交线段于，且，求.
【答案】(1)
(2)或36
【分析】（1）设，得到，得到方程，化简得到；
（2）设直线的方程为，与联立，得到两根之和，两根之积，设，根据，求出，进而求出，得到圆、圆相外切，分公切线与轴交点为，且在直线和公切线与轴交点为，且与直线垂直，两种情况，利用弦长公式求出答案.
【详解】（1）由题意可知，圆在轴上方，
设，，则，
由题意，得圆的半径，即，
两边平方得，
故的方程为；
（2）当直线的斜率不存在时，与无交点，舍去，
设直线的方程为，与联立得，，
恒成立，
设，则，
故，
则的中点，，
故轴为圆、圆的一条公切线，
设，因为，所以，
故，
又，故，即，
所以，解得，负值舍去，，
不妨令，
故，，此时，
故，
，
故圆、圆相外切，
如图1所示，此时公切线与轴交点为，且在直线上，
，
其中直线的方程为，即，
令得，故，
设直线，则点到直线的距离为1，
即，解得，
故直线，联立得，，
设，则，
故，
如图2，当公切线与直线垂直，
因为，所以，
故公切线的方程为，联立得，，
设，则，
故，
综上，或36.
【点睛】结论点睛：抛物线的相关结论，
中，过焦点的直线与抛物线交于两点，则以为直径的圆与轴相切，以为直径的圆与准线相切；
中，过焦点的直线与抛物线交于两点，则以为直径的圆与轴相切，以为直径的圆与准线相切.
1
2
3
4
5
6