2022-2023学年河南省新乡市封丘县九年级（上）期末数学试卷（含解析）

这是一份2022-2023学年河南省新乡市封丘县九年级（上）期末数学试卷（含解析），共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题：本题共10小题，每小题3分，共30分。在每小题给出的选项中，只有一项是符合题目要求的。
1.下列是二次根式的是( )
A. 12B. −2C. 3D. −2
2.“任意掷一枚质地均匀的骰子，掷出的点数是偶数”这个事件是( )
A. 必然事件B. 不可能事件C. 随机事件D. 确定事件
3.已知△ABC∽△DEF，且相似比为1：4，则△ABC与△DEF的面积比为( )
A. 1：2B. 1：4C. 1：16D. 16：1
4.下列计算正确的是( )
A. 2× 6=2 3B. 2 5−4 5=−2
C. 2+ 3= 5D. 8÷ 2=4
5.某种品牌的电动车经过四、五月份连续两次降价，每辆售价由3600元降到了3000元，设平均每月降低的百分率为x，根据题意可列出的方程是( )
A. 3000(1+x)2=3600B. 3000(1−x)2=3600
C. 3600(1+x)2=3000D. 3600(1−x)2=3000
6.在平面直角坐标系中，点A(sin30°,−cs60°)关于x轴对称的点的坐标是( )
A. (−12,− 32)B. (12,12)C. (12, 32)D. (−12,12)
7.如图，大树AB垂直于地面，为测树高，小明在D处测得∠ADB=30°，他沿BC方向走了16米，到达C处，测得∠ACB=15°，则大树AB的高度为( )
A. 6米B. 8米C. 10米D. 20米
8.定义运算：m☆n=n2−mn−1，例如：3☆2=22−3×2−1=−3.则方程2☆x=0的根的情况为( )
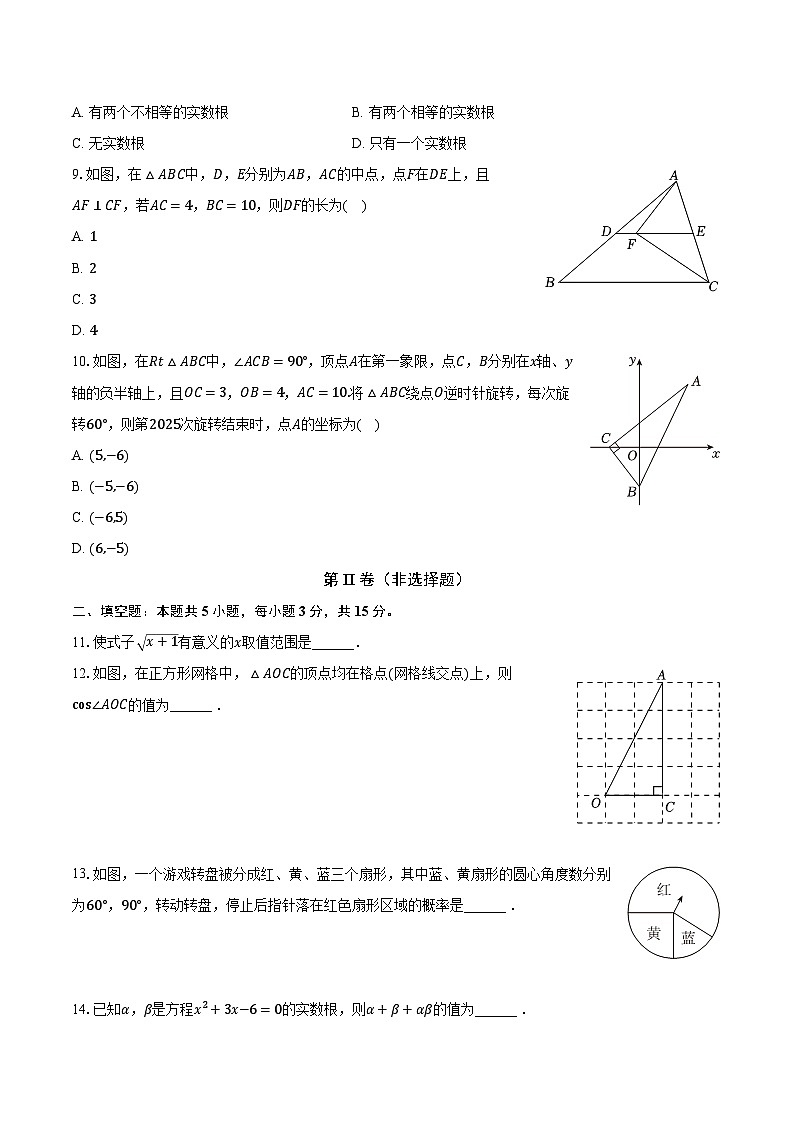
A. 有两个不相等的实数根B. 有两个相等的实数根
C. 无实数根D. 只有一个实数根
9.如图，在△ABC中，D，E分别为AB，AC的中点，点F在DE上，且AF⊥CF，若AC=4，BC=10，则DF的长为( )
A. 1
B. 2
C. 3
D. 4
10.如图，在Rt△ABC中，∠ACB=90°，顶点A在第一象限，点C，B分别在x轴、y轴的负半轴上，且OC=3，OB=4，AC=10.将△ABC绕点O逆时针旋转，每次旋转60°，则第2025次旋转结束时，点A的坐标为( )
A. (5,−6)
B. (−5,−6)
C. (−6,5)
D. (6,−5)
第II卷（非选择题）
二、填空题：本题共5小题，每小题3分，共15分。
11.使式子 x+1有意义的x取值范围是______．
12.如图，在正方形网格中，△AOC的顶点均在格点(网格线交点)上，则cs∠AOC的值为______ ．
13.如图，一个游戏转盘被分成红、黄、蓝三个扇形，其中蓝、黄扇形的圆心角度数分别为60°，90°，转动转盘，停止后指针落在红色扇形区域的概率是______ ．
14.已知α，β是方程x2+3x−6=0的实数根，则α+β+αβ的值为______ ．
15.如图，在△ABC中，∠B=90°，AB=2cm，BC=4cm，动点P从点A开始沿着边AB向点B以1cm/s的速度移动，动点Q从点B开始沿着边BC向点C以2cm/s的速度移动.若P，Q两点同时开始运动，当点P运动到终点B时，点Q也停止运动.在运动过程中，若以B，P，Q为顶点的三角形与△ABC相似，则运动时间为______ ．
三、解答题：本题共8小题，共75分。解答应写出文字说明，证明过程或演算步骤。
16.(本小题8分)
(1)计算： 48÷ 2+3 23− 54；
(2)解方程：x2−4x=6．
17.(本小题8分)
一天，甲、乙两人外出参观游玩，各自随机选择到大雁塔、曲江遗址公园、陕西历史博物馆、昆明池四个地点中的一个地点参观游玩．假设这两人选择到哪个地点参观游玩不受任何因素影响，上述四个地点中的每个被选到的可能性相同．
(1)甲选择到昆明池参观游玩的概率为______；
(2)用列表法或树状图法求甲、乙两人选择到同一个地点参观游玩的概率．
18.(本小题8分)
如图，在Rt△ABC中，∠C=90°．
(1)利用尺规作AB的垂直平分线，垂足为D，交AC于点E.(要求：不写作法，标明字母并保留作图痕迹)
(2)在(1)所作的图形中，当AB=10，BC=6时，求cs∠BAC的值及线段AE的长．
19.(本小题9分)
如图，在平面直角坐标系中，△ABC的顶点均在格点(网格线的交点)上，已知A(1,0)，B(2,4)，C(4,1)．
(1)以点O为位似中心，在第一象限画出△ABC的位似图形△A′B′C′，使△A′B′C′与△ABC的相似比为2：1.(A,B,C的对应点分别为A′，B′，C′)
(2)在(1)的条件下，写出点B′，C′的坐标并求出△A′B′C′的面积．
20.(本小题10分)
为测量图中铁塔AB的高度，小明利用自制的测角仪在D点测得塔顶A的仰角为37°，从点C向正前方行进12米到F处，再用测角仪在E点测得塔顶A的仰角为45°.已知测角仪CD的高度为1.5米，求铁塔AB的高度.(参考数据：cs37°≈45，sin37°≈35，tan37°≈34)
21.(本小题10分)
如图，张大伯家有一块长方形空地ABCD，长方形空地的长BC为 72m，宽AB为 32m，现要在空地中划出一块长方形地养鸡(即图中阴影部分)，其余部分种植蔬菜，长方形养鸡场的长为( 10+1)m，宽为( 10−1)m．
(1)长方形ABCD的周长是多少？(结果化为最简二次根式)
(2)若市场上蔬菜8元/千克，张大伯种植该种蔬菜，每平方米可以产15千克的蔬菜，张大伯如果将所种蔬菜全部销售完，销售收入为多少元？
22.(本小题10分)
某种商品的标价为80元/件，经过两次降价后的价格为64.8元/件，并且两次降价的百分率相同．
(1)求该商品每次降价的百分率．
(2)已知该商品进价为60元/件，经过市场调研发现，当以90元/件售出时，平均每天能售出20件，若每件降价2元，则每天可多售出10件，在每件降价幅度不超过10元的情况下，若每天盈利1125元，则每件商品应降价多少元？
23.(本小题12分)
综合与探究
问题背景：

(1)①如图1，在正方形ABCD中，E，N分别是AD，CD上的两点，连接AN，BE.若BE⊥AN，则ANBE的值为______ ．
②如图2，在矩形ABCD中，E是AD上的一点，N是CD上一点，连接BE，AN.若BE⊥AN，且AB=6，BC=4，则ANBE的值为______ ．
问题探究：
(2)如图3，在矩形ABCD中，E为边AD上的动点，F为边BC上的动点，M为边AB上的动点，连接EF，过点M作MN⊥EF于点O，交边CD于点N.若AB=m，AD=n，求MNEF的值．
问题拓展：
(3)如图4，把(2)中的条件改为“在四边形ABCD中，BC=CD，∠BCD=60°，∠ADC=90°，点F与点C重合，点M与点B重合，EF⊥MN”，请直接写出MNEF的值．
答案和解析
1.【答案】C
【解析】解：A. 12是整式，不是二次根式，故此选项不符合题意；
B.−2是整式，不是二次根式，故此选项不符合题意；
C. 3是二次根式，故此选项符合题意；
D， −2的补开方数是负数，没有意义，故此选项不符合题意；
故选：C．
根据二次根式的定义对各选项进行判断即可．
本题主要考查了二次根式的判断，正确掌握二次根式的定义：形如 a(a≥0)的式子是二次根式是解答本题的关键．
2.【答案】C
【解析】解：“任意掷一枚质地均匀的骰子，掷出的点数可能是偶数，有可能是奇数”，
∴“任意掷一枚质地均匀的骰子，掷出的点数是偶数”是随机事件；
故选：C．
根据事件发生的可能性大小判断即可．
本题考查的是必然事件、不可能事件、随机事件的概念，必然事件指在一定条件下，一定发生的事件．不可能事件是指在一定条件下，一定不发生的事件，不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件．
3.【答案】C
【解析】解：∵△ABC∽△DEF，
∴S△ABCS△DEF=(ABDE)2，
∵ABDE=14，
∴△ABC与△DEF的面积比是(14)2=1：16，
故选：C．
根据相似三角形的性质：相似三角形的面积之比等于相似比的平方，即可求出答案．
本题考查了相似三角形的性质的应用，注意：相似三角形的面积之比等于相似比的平方，而不等于相似比，题目比较典型，难度不大．
4.【答案】A
【解析】解：A、 2× 6= 12=2 3，故选项A计算正确，符合题意；
B、2 5−4 5=−2 5，原选项计算错误，故选项B不符合题意；
C、 2与 3不是同类二次根式，不能合并，故C不符合题意；
D、 8÷ 2= 4=2，原选项计算错误，故选项D不符合题意；
故选：A．
根据二次根式的加法，乘法，除法，二次根式的性质，进行计算逐一判断即可解答解答：
本题考查了二次根式的加、减、乘、除运算，准确熟练地进行计算是解题的关键．
5.【答案】D
【解析】解：设平均每月降低的百分率为x，
根据题意，可得：3600(1−x)2=3000．
故选：D．
根据原售价×(1−降低率)2=两次降价后的售价，然后即可列出方程．
本题考查了由实际问题抽象出一元二次方程，解本题关键在于理解题意列出方程．
6.【答案】B
【解析】解：∵sin30°=12，−cs60°=−12，
∴点A(12,−12)
∴点A关于x轴对称点的坐标是(12,12)．
故选：B．
先利用特殊三角函数值求出点A坐标，再根据关于x轴对称的点的坐标特点求解．
本题考查的是特殊三角函数值、关于坐标轴对称的点的性质，正确把握横纵坐标关系是解题关键．
7.【答案】B
【解析】解：∵∠ADB=30°，∠ACB=15°，
∴∠CAD=∠ACD=15°，
∵DC=16米，
∴AD=16米，
∵∠ADB=30°，AB垂直于地面，
∴AB=12AD=8米，
故选：B．
根据∠ADB=30°，∠ACB=15°即可得到∠CAD=∠ACD=15°，再根据直角三角形中30°角所对直角边等于斜边一半即可得到答案．
本题考查解直角三角形，等腰三角形性质，三角形内外角关系及直角三角形中30°角所对直角边等于斜边一半，解题的关键是得到等腰三角形．
8.【答案】A
【解析】解：根据题意得x2−2x−1=0，
∵Δ=(−2)2−4×(−1)=8>0，
∴方程有两个不相等的实数根．
故选：A．
根据新运算得到x2−2x−1=0，再计算判别式的值，然后根据判别式的意义确定方程根的情况．
此题考查了根的判别式，一元二次方程ax2+bx+c=0(a≠0)的根与Δ=b2−4ac有如下关系：(1)Δ>0⇔方程有两个不相等的实数根；(2)Δ=0⇔方程有两个相等的实数根；(3)Δ<0⇔方程没有实数根．
9.【答案】C
【解析】解：∵D、E分别为AB、AC的中点，BC=10，
∴DE=12BC=5，
∵AF⊥CF，
∴∠AFC=90°，
∵E为AC的中点，AC=4，
∴FE=12AC=2，
∴DF=DE−FE=3，
故选：C．
根据三角形中位线定理求出DE，根据直角三角形的性质求出FE，计算即可．
本题考查的是三角形中位线定理、直角三角形的性质，解题的关键是掌握三角形的中位线平行于第三边，并且等于第三边的一半．
10.【答案】B
【解析】解：如图，过点A作AT⊥x轴于点T．
∵OC=3，OB=4，∠COB=90°，
∴BC=5，
∵∠ATC=∠COB=90°，
∴∠CAT+∠ACT=90°，∠ACT+∠BCO=90°，
∴∠CAT=∠BCO，
∴△ATC∽△COB，
∴ATOC=CTOB=ACBC，
即AT3=CT4=105，
∴AT=6，CT=8，
∴OT=CT−OC=8−3=5，
∴A(5,6)．
∵△ABC绕点O逆时针旋转，每次旋转60°，发现规律：旋转6次一个循环．
∵2025÷6=337⋯⋯3，
∴此时点A位于第三象限，且与点A关于原点成中心对称，
∴第2025次旋转结束时，点A的坐标为(−5,−6)，
故选：B．
首先过点A作AT⊥x轴于点T，得到△ATC∽△COB，进而得出A点坐标，再根据绕原点旋转一定角度的点的坐标得出旋转结束后的A点坐标即可．
本题考查了相似三角形的判定，相似三角形的性质和求绕原点旋转一定角度的点的坐标，熟练掌握相似三角形的判定和性质是解题的关键．
11.【答案】x≥−1
【解析】解：根据题意得：x+1≥0，
解得x≥−1．
故答案为：x≥−1．
本题主要考查自变量的取值范围，函数关系中主要有二次根式．根据二次根式的意义，被开方数是非负数．
本题考查二次根式有意义的条件，比较简单，注意掌握二次根式的意义，被开方数是非负数．
12.【答案】 55
【解析】解：∵正方形网格中，△AOC的顶点均在格点上，
∴∠ACO=90°，OC=2，AC=4，
∴AO= OC2+AC2=2 5，
∴cs∠AOC=OCAO= 55，
故答案为： 55．
直接根据图象计算即可．
本题考查了锐角三角函数的概念，熟练掌握锐角三角函数的定义是解答本题的关键．
13.【答案】712
【解析】解：红色部分所在的圆心角的度数为360°−60°−90°=210°，
因此红色部分所占整体的210360=712，即转动转盘，停止后指针落在红色区域的概率为712，
故答案为：712．
求出红色部分所占整体的几分之几即可．
本题考查几何概率，求出相应部分所占整体的几分之几是解决问题的关键．
14.【答案】−9
【解析】解：∵α、β是方程x2+3x−6=0的两根，
∴α+β=−3，αβ=−6，
∴α+β+αβ=−3−6=−9，
故答案为：−9．
由根与系数关系找出α+β，αβ即可求出答案．
本题考查了根与系数的关系，根据根与系数关系找出α+β，αβ是解决本题的关键．
15.【答案】25s或1s
【解析】解：设点P运动的时间为t s，则AP=t cm，BQ=2t cm，
∴BP=(2−t)cm，
∵∠B=∠B，
∴当∠BPQ=∠C时，△QBP～△ABC，
∴BPBC=BQAB，
∴2−t4=2t2，
解得t=25；
∵∠B=∠B，
∴当∠BPQ=∠A时，△PBQ～△ABC，
∴BPAB=BQBC，
∴2−t2=2t4，
解得t=1．
综上所述，运动时间为25s或1s．
故答案为：25s或1s．
设点P运动的时间为t s，则AP=t cm，BQ=2tcm，BP=(2−t)cm，再分两种情况求t的值，一是∠BPQ=∠C，则△QBP～△ABC，可列方程2−t4=2t2；二是∠BPQ=∠A，则△PBQ～△ABC，可列方程2−t2=2t4，解方程求出相应的t的值即可．
此题重点考查相似三角形的判定与性质、动点问题的求解、数形结合与分类讨论数学思想的运用等知识与方法，正确地用代数式表示相似三角形的对应边的长度是解题的关键．
16.【答案】解：(1)原式= 24+ 6− 54
=2 6+ 6−3 6
=0．
(2)x2−4x+4=6+4，
(x−2)2=10，
x−2= 10或x−2=− 10，
解得x1= 10+2,x2=− 10+2．
【解析】(1)先将二次根式化简，然后计算加减法即可；
(2)根据配方法解一元二次方程即可．
本题主要考查二次根式的加减运算及解一元二次方程，熟练掌握运算法则是解题关键．
17.【答案】14
【解析】解：(1)由题意得，甲选择到昆明池参观游玩的概率为14，
故答案为：14；
(2)记大雁塔、曲江遗址公园、陕西历史博物馆、昆明池四个地点分别为A、B、C、D，
画树状图如下：
由树状图可知，共有16种等可能的结果，其中甲、乙两人选择到同一个地点参观游玩的有4种结果，
∴甲、乙两人选择到同一个地点参观游玩的概率为416=14．
(1)直接利用概率公式求解即可；
(2)记大雁塔、曲江遗址公园、陕西历史博物馆、昆明池四个地点分别为A、B、C、D，画出树状图得出所有等可能结果，从中找到甲、乙两人选择到同一个地点参观游玩的结果数，然后根据概率公式求解可得．
本题考查了概率公式，用列表法或画树状图法求概率，利用列表法或树状图法展示所有等可能的结果n，再从中选出符合事件A或B的结果数目m，然后利用概率公式求事件A或B的概率．
18.【答案】解：(1)如图，DE即为所求．

(2)在Rt△ABC中，∠C=90°，AB=10，BC=6，
∴AC= AB2−BC2= 102−62=8，
∴cs∠BAC=ACAB=810=45．
∵DE垂直平分AB，
∴AD=12AB=5,∠ADE=90°，cs∠BAC=ADAE=5AE=45，可得AE=254．
【解析】(1)根据垂直平分线的作法，求解即可；
(2)利用勾股定理以及三角函数的定义求解即可．
此题考查了三角函数的定义，解直角三角形以及垂直平分线的作法，解题的关键是灵活利用相关基础知识进行求解．
19.【答案】解：(1)如图，△A′B′C′即为所求．

(2)由图象可知：B′(4,8)，C′(8,2)．
S△A′B′C′=6×8−12×2×8−12×6×2−12×6×4=22．
【解析】(1)直接利用位似图形的性质得出对应点位置进而得出答案；
(2)结合图形写出B′，C′的坐标，再运用割补法求出△A′B′C′的面积即可．
此题主要考查了位似变换，正确得出对应点位置是解题关键．
20.【答案】解：由题意得，CF=12米，DC=1.5米，
∵∠AGD=90°，∠ABC=∠EFC=∠DCF=∠CDG=∠BGE=90°，
∴四边形EFCD是矩形，四边形GBCD是矩形，
∴CF=DE=12米，DC=GB=1.5米，
∵∠AEG=45°，
∴AG=GE，
设GE=x(米)，
∴AG=GE=x(米)，
∵在Rt△AGD中，tan∠ADG=AGGD=34，
∴tan∠ADG=xx+12=34，
解得：x=36(米)，
∵AB=AG+GB，
∴AB=36+1.5≈37.5(米)．
答：铁塔AB的高度为37.5米．
【解析】根据题意，得CF=12米，DC=1.5米，根据矩形的判定和性质，得四边形EFCD是矩形，再根据∠AEG=45°，则设AG=GE=x(米)，根据直角三角形中，tan∠ADG=AGGD，解出x，根据AB=AG+GB，即可．
∖ 本题考查解直角三角形的知识，解题的关键是掌握直角三角形的性质，解直角三角形中正切值的运用．
21.【答案】解：(1)长方形ABCD的周长=2×( 72+ 32)=2×(6 2+4 2)=20 2(m)．
答：长方形ABCD的周长是20 2m；
(2)蔬菜地的面积= 72× 32−( 10+1)×( 10−1)
=48−(10−1)=39(m2).
39×8×15=4680(元)．
答：张大伯如果将所种蔬菜全部销售完，销售收入为4680元．
【解析】(1)利用长方形的周长公式即可求解；
(2)先求得蔬菜地的面积，再计算收入即可求解．
本题考查了二次根式的应用，掌握二次根式的混合运算的法则是解题的关键．
22.【答案】解：(1)设该商品每次降价的百分率为x．
依题意，得80(1−x)2=64.8，
解得x1=0.1=10%，x2=1.9(不合题意，舍去)．
答：该商品每次降价的百分率为10%．
(2)设每件商品应降价x元．
根据题意，得(90−x−60)(20+5x)=1125，
解得x1=5，x2=21．
∵降价幅度不超过10元，
∴x=5．
答：每件商品应降价5元．
【解析】(1)直接代入公式a(1−x)2=b即可求出降价率；
(2)先设未知数，再利用单个利润乘以数量等于总利润列出方程，再解方程即可，要利用每件降价幅度不超过10元排除其中一个答案．
本题考查平均增长率问题和一元二次方程的实际问题，细心审题和记忆理解公式是解题的关键．
23.【答案】1 23
【解析】解：(1)①∵正方形ABCD，
∴∠BAE=∠D=90°
∴∠BAN+∠NAD=90°．
∵BE⊥AN，
∴∠BAN+∠ABE=90°，
∴∠NAD=∠ABE，
∵AB=AD，
∴△ABE≌△DAN(ASA)
∴BE=AN，
∴ANBE=1，
故答案为：1；
②∵矩形ABCD，
∴∠BAE=∠D=90°
∴∠BAN+∠NAD=90°．
∵BE⊥AN，
∴∠BAN+∠ABE=90°，
∴∠NAD=∠ABE，
∴△ABE∽△DAN
∴ANBE=ADAB=23，
故答案为：23；
(2)如图3，过点A作AQ//MN交CD于点Q，过点B作BK//EF交AD于点K．
∵四边形ABCD是矩形，
∴BC/​/AD，AB/​/CD．
∵MN//AQ，BK//EF，
∴四边形AMNQ和四边形BFEK是平行四边形，
∴AQ=MN，BK=FE．
∵MN⊥EF，
∴AQ⊥BK，
∴∠QAD+∠AKB=90°．
∵∠KBA+∠AKB=90°，
∴∠KBA=∠QAD．
∵∠BAK=∠ADQ=90°，
∴△ABK∽△DAQ，
∴MNEF=AQBK=ADAB=nm．
(3)MNEF= 32.理由如下：
如图4，连接BD，过点B作BH⊥CD于点H．
∵∠BCD=60°，BC=CD，
∴△BCD是等边三角形，
∴BC=CD=BD．
∵BH⊥CD，
∴∠BHC=∠BHD=90°．
在Rt△BCH中，sin∠BCD=BHBC= 32．
∵BN⊥CE，
∴∠NOC=90°，
∴∠OBH+∠BNH=∠BNH+∠DCE=90°，
∴∠OBH=∠DCE．
∵∠ADC=∠BHN=90°，
∴△BHN∽△CDE，
∴BNCE=BHCD=BHBC= 32，
∴MNEF= 32．
(1)①根据正方形的性质及全等三角形的判定和性质即可得出结果；
②根据矩形的性质及相似三角形的判定和性质求解即可；
(2)过点A作AQ//MN交CD于点Q，过点B作BK//EF交AD于点K.根据平行四边形的判定得出四边形AMNQ和四边形BFEK是平行四边形，再由相似三角形的判定和性质即可求解；
(3)连接BD，过点B作BH⊥CD于点H.由等边三角形的判定和性质得出BC=CD=BD，再由正弦函数及相似三角形的判定和性质求解即可．
本题主要考查矩形和正方形的性质，全等三角形的判定和性质，相似三角形的判定和性质及正弦函数的定义，理解题意，作出辅助线，综合运用这些知识点是解题关键．