2024年中考数学二次函数压轴题-平行四边形存在性（训练篇）（试题+解析）

这是一份2024年中考数学二次函数压轴题-平行四边形存在性（训练篇）（试题+解析），文件包含2024年中考数学二次函数压轴题-平行四边形存在性训练篇试题docx、2024年中考数学二次函数压轴题-平行四边形存在性训练篇解析docx等2份试卷配套教学资源，其中试卷共76页， 欢迎下载使用。
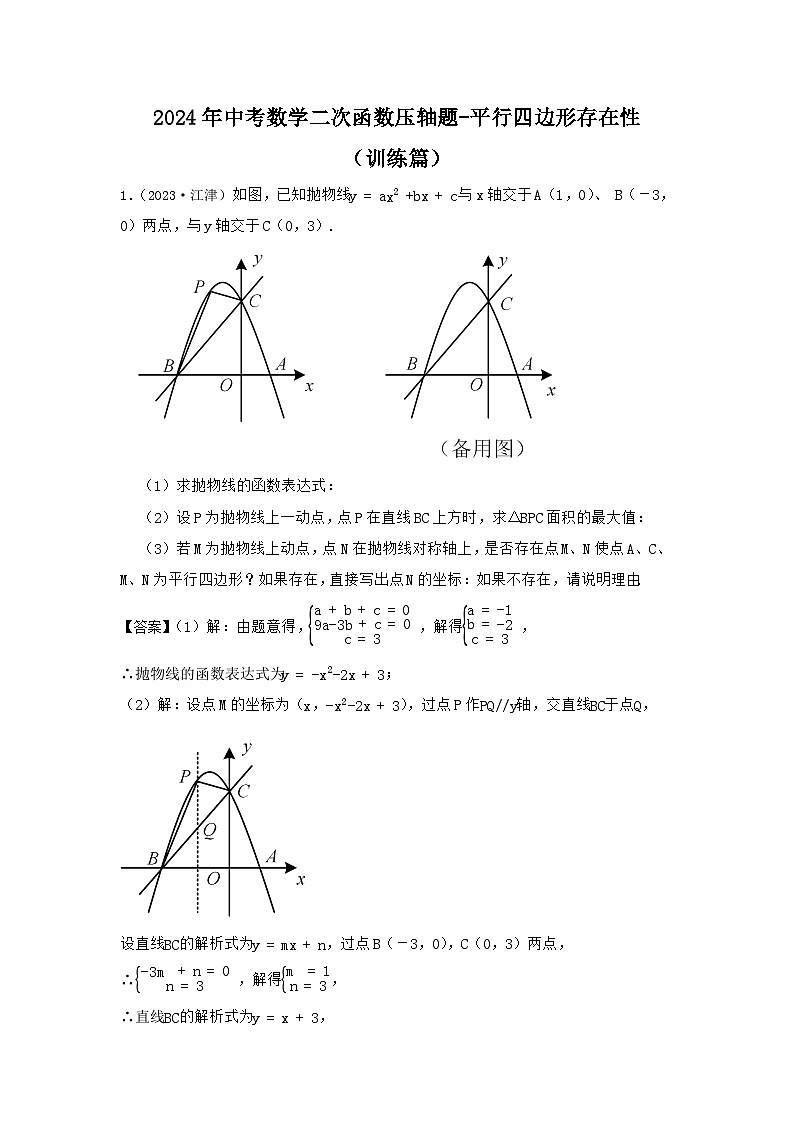
1．（2023·江津）如图，已知抛物线y=ax2+bx+c与x轴交于A（1，0）、 B（－3，0）两点，与y轴交于C（0，3）.
（1）求抛物线的函数表达式：
（2）设P为抛物线上一动点，点P在直线BC上方时，求△BPC面积的最大值：
（3）若M为抛物线上动点，点N在抛物线对称轴上，是否存在点M、N使点A、C、M、N为平行四边形？如果存在，直接写出点N的坐标：如果不存在，请说明理由.
2．（2023·威远）如图，在平面直角坐标系中，抛物线y=ax2+bx−3(a≠0)与x轴交于A(−1，0)，B(3，0)两点，与y轴交于C点.
（1）求抛物线的函数表达式；
（2）点P是直线BC下方抛物上一动点，连接PB，PC，求△PBC面积的最大值以及此时点P的坐标；
（3）在（2）中△PBC的面积取得最大值的条件下，将该抛物线沿水平方向向左移动2个单位，平移后的抛物线顶点坐标为Q，M为y轴上一点，在平移后的抛物线上确定一点N，使得以点P，Q，M，N为顶点的四边形是平行四边形，写出所有符合条件的N的坐标，并写出求解点N的坐标的其中一种情况的过程.
3．（2023·朝阳）抛物线y=x2+bx-3经过(-2，5)，点A坐标为(m，0)，点B是抛物线上一点，其横坐标为1-m．
（1）求抛物线解析式并求顶点坐标．
（2）当A在抛物线上时，求m的值．
（3）当m> 0时，设抛物线与x轴右侧的交点为点P，点B和点P之间(包括B、P)的最高点和最低点纵坐标之差为3+m，求点A的坐标．
（4）点M(1-m，3-2m)，连结AM、BM为边构建平行四边形AMBN，当▱ AMBN的面积被x轴分成1：3两部分时，求m的值．
4．（2023·茶山）在平面直角坐标系中，抛物线y＝ax2+bx+c（a≠0）经过点A（-1，0）和B（0，3），其顶点的横坐标为1．
（1）求抛物线的表达式．
（2）若直线x＝m与x轴交于点N，在第一象限内与抛物线交于点M，当m取何值时，使得AN+MN有最大值，并求出最大值．
（3）若点P为抛物线y＝ax2+bx+c（a≠0）的对称轴上一动点，将抛物线向左平移1个单位长度后，Q为平移后抛物线上一动点．在（2）的条件下求得的点M，是否能与A、P、Q构成平行四边形？若能构成，求出Q点坐标；若不能构成，请说明理由．
5．（2023·长宁模拟）已知抛物线y=ax2+bx+c(a>0)与x轴交于点A(1，0)和B(4，0)，与y轴交于点C，O为坐标原点，且OB=OC．
（1）求抛物线的解析式；
（2）如图1，点P是线段BC上的一个动点（不与点B、C重合），过点P作x轴的垂线交抛物线于点Q，连接OQ．当四边形OCPQ恰好是平行四边形时，求点Q的坐标；
（3）如图2，在（2）的条件下，D是OC的中点，过点Q的直线与抛物线交于点E，且∠DQE=2∠ODQ，在直线QE上是否存在点F，使得△BEF与△ADC相似？若存在，求点F的坐标：若不存在，请说明理由．
6．（2023·历下模拟）如图1，抛物线y=ax2+32x+c与x轴交于点A、B(4，0)（A点在B点左侧），与y轴交于点C(0，6)，点P是抛物线上一个动点，连接PB，PC，BC
（1）求抛物线的函数表达式；
（2）如图2所示，当点P在直线BC上方运动时，连接AC，求四边形ABPC面积的最大值，并写出此时P点坐标．
（3）若点M是x轴上的一个动点，点N是抛物线上一动点，P的横坐标为3．试判断是否存在这样的点M，使得以点B，M，N，P为顶点的四边形是平行四边形，若存在，请直接写出点M的坐标；若不存在，请说明理由．
7．（2023·睢宁）如图，在平面直角坐标系中，已知抛物线y＝ax2+bx+2（a≠0）与x轴交于A（-1，0），B（3，0）两点，与y轴交于点C，连接BC.
（1）求该抛物线的解析式，并写出它的对称轴；
（2）点D为抛物线对称轴上一点，连接CD、BD，若∠DCB＝∠CBD，求点D的坐标；
（3）若点N为抛物线对称轴上一点，抛物线上是否存在点M，使得以B，C，M，N为顶点的四边形是平行四边形？若存在，请直接写出所有满足条件的点M的坐标；若不存在，请说明理由.
（4）若点P为坐标系中的一点，OP＝4，则2PC+PB的最小值为 .
8．（2023·崇左）已知抛物线y=ax2+bx+3(a≠0)交x轴于A(1，0)和B(−3，0)，交y轴于C.
（1）求抛物线的解析式；
（2）若M为抛物线上第二象限内一点，求使△MBC面积最大时点M的坐标；
（3）若F是对称轴上一动点，Q是抛物线上一动点，是否存在F、Q，使以B、C、F、Q为顶点的四边形是平行四边形？若存在，直接写出点Q的坐标.
9．（2023·中山）已知抛物线y=ax2+bx+c关于y轴对称，与x轴交于A、B两点，点A坐标为(−1，0)，抛物线还经过点(−3，8)．
（1）求抛物线的解析式；
（2）已知点C在y轴上，在抛物线上是否存在点D，使以A、B、C、D为顶点的四边形是平行四边形？若存在，请求出点D的坐标；若不存在，请说明理由．
10．（2023·合川）已知抛物线y=ax2+bx+3的图象与x轴相交于点A和点B(1，0)，与y轴交于点C，连接AC，有一动点D在线段AC上运动，过点D作x轴的垂线，交抛物线于点E，交x轴于点F，AB=4，设点D的横坐标为m.
（1）连接AE，CE则△ACE的最大面积为 ；
（2）当m=−2时，在平面内存在点Q，使以B，C，E，Q为顶点的四边形为平行四边形，请写出点Q的坐标 .
11．（2023·阳西）已知抛物线y=x2+bx+c与x轴相交于点A(−1，0)，B(3，0)，与y轴相交于点C．
（1）求抛物线的表达式；
（2）如图1，将直线BC间上平移，得到过原点O的直线MN．点D是直线MN上任意一点．
①当点D在抛物线的对称轴l上时，连接CD，关x轴相交于点E，水线段OE的长；
②如图2，在抛物线的对称轴l上是否存在点F，使得以B，C，D，F为顶点的四边形是平行四边形？若存在，求出点F与点D的坐标；若不存在，请说明理由．
12．（2023·东莞）如图，抛物线y=ax2+bx+3与x轴交于A(−3，0)，B(1，0)两点，与y轴交于点C．
备用图
（1）求抛物线的解析式；
（2）点P是抛物线上的动点，且满足SΔPAO=2SΔPCO，求出P点的坐标；
（3）连接BC，点E是x轴一动点，点F是抛物线上一动点，若以B、C、E、F为顶点的四边形是平行四边形时，请直接写出点F的坐标．
13．（2023·浑南）如图1，平面直角坐标系中，O是坐标原点，二次函数y=x2+bx+c的图象与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C(0，−3)，点B坐标是(3，0)，点P是抛物线的顶点．
（1）请直接写出二次函数的表达式及顶点P的坐标；
（2）如图2，设二次函数图象的对称轴PH与x轴交于点H，
①连接AC，BC，CP，点D为对称轴PH上的一点，且△CDP与△ABC相似，求点D的坐标；
②点M为对称轴PH上一点且在x轴下方，在x轴负半轴上有一点E，在y轴负半轴上有一点F，且满足OF=4EO=4MH，已知点N在抛物线上，以E，F，M，N为顶点的四边形为平行四边形，请直接写出点E的坐标．
14．（2023·舟山）如图，在直角坐标系中，已知抛物线y=ax2+bx+c经过原点，与x轴交于点A(5，0)，点B(4，2)是抛物线上的一点，连接OB，点C是OB上的任意一点，它的横坐标为m，过点C作CD⊥x轴，与抛物线交于点D，过点B作BE⊥x轴于点E．
（1）求直线OB和抛物线的解析式；
（2）设△DOB的面积为S，求S与m的函数关系式．
（3）当m为何值时，四边形DCEB是平行四边形？为什么？
15．（2023·南宁）如图，抛物线经过A（-2，0），C（0，-3）两点，且对称轴为直线x=12.
（1）求抛物线的函数解析式；
（2）若直线y＝kx-5与抛物线交于点M，N，交x轴于点B，交y轴于点P，连接CN，且tan∠OPM=12.
①求△CMN的面积；
②在平面内是否存在点一是E，使E，C，N，M四点能构成平行四边形，如果存在，请直接写出点E的坐标.
16．（2023·文登）如图，在平面直角坐标系中，抛物线y＝12x2＋bx＋c经过点A（-4，0），点M为抛物线的顶点，点B在y轴上，且OA＝OB，直线AB与抛物线在第一象限交于点C（2，6）．
（1）求抛物线的解析式及顶点M的坐标；
（2）求直线AB的函数解析式及sin∠ABO的值；连接OC．若过点O的直线交线段AC于点P，将三角形AOC的面积分成1：2的两部分，请求出点P的坐标；
（3）在坐标平面内是否存在点N，使以点A、O、C、N为顶点的四边形是平行四边形？若存在，请直接写出点N的坐标；若不存在，请说明理由．
17．（2023·阳信）如图，已知抛物线y=ax2+bx+c的顶点为A(4，3)，与y轴相交于点B(0，-5)，对称轴为直线l，点M是线段AB的中点．
（1）求抛物线的表达式；
（2）请求出点M的坐标及直线AB的表达式；
（3）设动点P，Q分别在抛物线和对称轴l上，当以A，P，Q，M为顶点的四边形是平行四边形时，求P，Q两点的坐标．
18．（2023·临淄）如图，抛物线y=ax2+bx+52与直线AB交于点A(−1，0)，B(4，52)．点D是抛物线上A，B两点间的一个动点（不与点A，B重合），直线CD与y轴平行，交直线AB于点C，连接AD，BD．
（1）求抛物线的解析式；
（2）设点D的横坐标为m，△ADB的面积为S，求S关于m的函数关系式，并求出当S取最大值时的点C的坐标；
（3）点D为抛物线的顶点，点P是抛物线上的动点，点Q是直线AB上的动点．当以点P，Q，C，D为顶点的四边形是平行四边形时，求出点Q的坐标．
19．（2023·荣县）如图，已知直线AB与抛物线C：y=ax2+2x+c相交于点A(−1，0)和点B(2， 3)两点.
（1）求抛物线C函数表达式；
（2）若点M是位于直线AB上方抛物线上的一动点，以MA、MB为相邻的两边作平行四边形MANB，当平行四边形MANB的面积最大时，求此时平行四边形MANB的面积S及点M的坐标；
（3）在抛物线C的对称轴上是否存在定点F，使抛物线C上任意一点P到点F的距离等于到直线y＝174的距离？若存在，求出定点F的坐标；若不存在，请说明理由.
20．（2023·易县）如图，直线y=−12x+2与x轴交于点B，与y轴交于点C，对称轴为x=32的抛物线经过B，C两点，与x轴负半轴交于点A．
（1）求抛物线的解析式；
（2）P为抛物线上的一点，连接AP，将线段AP绕点A顺时针旋转90°得线段AQ，当点Q到对称轴距离为12时，求点P的坐标；
（3）M为抛物线上的动点，N在直线BC上，当以O，C，M，N为顶点的四边形为平行四边形时，直接写出点N的坐标．