2022-2023学年内蒙古赤峰市红山区高二（上）期末数学试卷（理科）

这是一份2022-2023学年内蒙古赤峰市红山区高二（上）期末数学试卷（理科），共27页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．（5分）方程（2x﹣3）2+（y+2）2＝0表示的曲线是（ ）
A．一个点B．两条直线C．一个圆D．两个点
2．（5分）把二进制数111（2）化为十进制数为（ ）
A．2B．4C．7D．8
3．（5分）甲、乙两名同学12次考试中数学成绩的茎叶图如图所示，则下列说法正确的是（ ）
A．甲同学比乙同学发挥稳定，且平均成绩也比乙同学高
B．甲同学比乙同学发挥稳定，但平均成绩比乙同学低
C．乙同学比甲同学发挥稳定，且平均成绩也比甲同学高
D．乙同学比甲同学发挥稳定，但平均成绩比甲同学低
4．（5分）来自澳大利亚的心理学家Michael White设计出了一种被人称为“怀特错觉”的光学戏法．这类型的图片只有三种颜色：黑、白、灰，但大多数人都会看到四种颜色．这是因为灰色的色块嵌入了白色和黑色条纹中，从视觉上看，在所调查的100名调查者中，有55人认为图中有4种颜色，而在被调查者所列举的颜色中，有40人没有提到白色（他们认为白色是背景颜色，不算在图片颜色之中），估计在人群中产生怀特错觉的概率约为（ ）
A．0.45B．0.55C．0.05D．0.95
5．（5分）命题“存在实数x，使x＞1”的否定是（ ）
A．对任意实数x，都有x＞1
B．不存在实数x，使x≤1
C．对任意实数x，都有x≤1
D．存在实数x，使x≤1
6．（5分）已知x，y的取值如下表所示：
如果y与x呈线性相关，且线性回归方程为，则b＝（ ）
A．B．C．D．
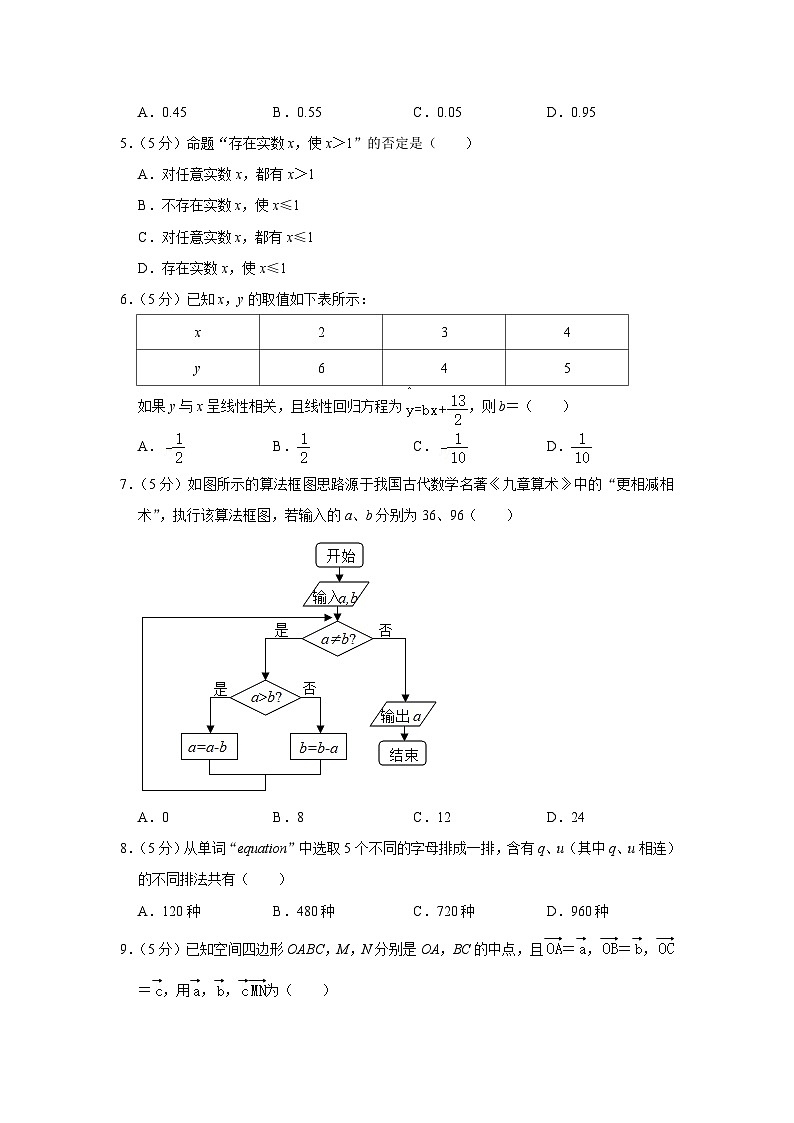
7．（5分）如图所示的算法框图思路源于我国古代数学名著《九章算术》中的“更相减相术”，执行该算法框图，若输入的a、b分别为36、96（ ）
A．0B．8C．12D．24
8．（5分）从单词“equatin”中选取5个不同的字母排成一排，含有q、u（其中q、u相连）的不同排法共有（ ）
A．120种B．480种C．720种D．960种
9．（5分）已知空间四边形OABC，M，N分别是OA，BC的中点，且＝，＝，＝，用，，为（ ）
A．++B．﹣+
C．﹣++D．﹣+﹣
10．（5分）希尔宾斯基三角形是一种分形，由波兰数学家希尔宾斯基在1915年提出，先作一个正三角形（即以原三角形各边的中点为顶点的三角形），然后在剩下的小三角形中又挖去一个“中心三角形”，我们用白色代表挖去的面积（我们称黑三角形为希尔宾斯基三角形）．在如图第3个大正三角形中随机取点，则落在黑色区域的概率为（ ）
A．B．C．D．
11．（5分）已知抛物线C：y2＝8x焦点为F，A是C上一点，O为坐标原点，则|AF|＝（ ）
A．B．3C．D．4
12．（5分）若直线y＝x+b与曲线有公共点，则实数b的取值范围为（ ）
A．B．C．D．[﹣2，2]
13．（5分）已知函数f（x）＝则关于x的方程f2（x）+bf（x）+c＝0有5个不同实数解的充要条件是（ ）
A．b＜﹣2 且 c＞0B．b＞﹣2 且 c＜0
C．b＜﹣2 且 c＝0D．b≥﹣2 且 c＝0
14．（5分）函数f（x）＝x2﹣2x，g（x）＝ax+2（a＞0），对∀x1∈[﹣1，2]，∃x0∈[﹣1，2]，使g（x1）＝f（x0），则a的取值范围是（ ）
A．B．C．[3，+∞）D．（0，3]
二、填空题（共6小题，每小题5分，本题共20分．请把正确答案填在答题卡中相应题号的横线上）
15．（5分）某中学有高中生3500人，初中生1500人，为了解学生的学习情况，则应从高中生中抽取 人．
16．（5分）的展开式中的常数项是： ．（请用数字作答）
17．（5分）圆x2+y2﹣2x﹣5＝0与圆x2+y2+2x﹣4y﹣4＝0的交点为A，B，则线段AB的垂直平分线方程为 ．
18．（5分）在正方体ABCD﹣A1B1C1D1中，M，N分别为AD，C1D1的中点，O为侧面BCC1B1的中心，则异面直线MN与OD1所成角的余弦值为 ．
19．（5分）已知双曲线的左、右焦点分别为F1，F2，点P为双曲线C右支上一点，直线PF1与圆x2+y2＝a2相切，且∠F1PF2＝∠PF1F2，则双曲线C的离心率为 ．
20．（5分）F1，F2分别是双曲线＝1的左、右焦点，P为双曲线右支上一点1F2的内心，且＝﹣λ，则λ＝ ．
三、解答题（本大题共7小题，共70分．解答应写出文字说明、证明过程或演算步骤）
21．（10分）已知p：﹣2＜a＜2，q：关于x的方程x2﹣x+a＝0有实数根．
（1）若q为真命题，求实数a的取值范围；
（2）若p∨q为真命题，￢q为真命题，求实数a的取值范围．
22．（10分）求解下列问题：
（1）求过直线x﹣y﹣5＝0与直线x+y﹣3＝0的交点，且与直线3x﹣4y+6＝0平行的直线方程；
（2）求以点（1，2）为圆心，与直线4x+3y﹣35＝0相切的圆的方程．
23．（10分）开学初学校进行了一次摸底考试，物理老师为了了解自己所教的班级参加本次考试的物理成绩的情况，从参考的本班同学中随机抽取n名学生的物理成绩（满分100分），将所得数据进行分析整理后画出频率分布直方图如图所示，已知抽取的学生中成绩在[50
（1）求n的值，并估计本班参考学生的平均成绩；
（2）已知抽取的n名参考学生中，在[90，100]的人中，现从[90，100]的人中随机抽取2人参加物理竞赛
24．（10分）某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系，他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数，得到如下资料：
（1）求出y关于x的线性回归方程；
（2）如果7月10号昼夜温差为8°C，预测因患感冒而就诊的人数（结果保留整数）．
附：回归方程中斜率和截距的最小二乘估计公式分别为：，．
25．（10分）如图，四边形ABCD为正方形，E，F分别为AD，以DF为折痕把△DFC折起，使点C到达点P的位置
（1）证明：平面PEF⊥平面ABFD；
（2）求DP与平面ABFD所成角的正弦值．
26．（10分）已知椭圆C中心在坐标原点，焦点在x轴上，且过点P，B两点（A，B两点不是左右顶点），若直线l的斜率为时上．
（Ⅰ）求椭圆C的方程．
（Ⅱ）若以A，B两点为直径的圆过椭圆的右顶点，则直线l是否经过定点，求出定点坐标，若不是
27．（10分）已知椭圆，四个点P1（1，1），P2（0，1），，中恰有三点在椭圆C上．
（1）求椭圆C的方程；
（2）设直线l：y＝kx+m（m≠1）与椭圆C相交于A，B两点．若直线P2A与直线P2B的斜率的和为﹣1，判断直线l是否经过定点，若过定点；若不过定点，请说明理由．
2022-2023学年内蒙古赤峰市红山区高二（上）期末数学试卷（理科）
参考答案与试题解析
一、选择题（共14小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）
1．（5分）方程（2x﹣3）2+（y+2）2＝0表示的曲线是（ ）
A．一个点B．两条直线C．一个圆D．两个点
【分析】根据题意可得，解得x，y的值，即可得到答案．
【解答】解：由方程（2x﹣3）6+（y+2）2＝4，可得，
解得，
所以方程（2x﹣3）2+（y+5）2＝0表示点．
故选：A．
【点评】本题考查曲线方程，考查运算求解能力，属于基础题．
2．（5分）把二进制数111（2）化为十进制数为（ ）
A．2B．4C．7D．8
【分析】将二进制数转化为十进制数，可以用每个数位上的数字乘以对应的权重，累加后，即可得到答案．
【解答】解：111（2）＝1×26+1×28+1＝7
故选：C．
【点评】本题考查的知识点是不同进制之间的转换，其中其它进制转为十进制方法均为累加数字×权重，十进制转换为其它进制均采用除K求余法．
3．（5分）甲、乙两名同学12次考试中数学成绩的茎叶图如图所示，则下列说法正确的是（ ）
A．甲同学比乙同学发挥稳定，且平均成绩也比乙同学高
B．甲同学比乙同学发挥稳定，但平均成绩比乙同学低
C．乙同学比甲同学发挥稳定，且平均成绩也比甲同学高
D．乙同学比甲同学发挥稳定，但平均成绩比甲同学低
【分析】根据茎叶图的数据分布，即可直接求解．
【解答】解：由茎叶图分布可知，乙的数据更多集中在114﹣128之间，
乙同学平均成绩比甲同学高，乙同学数据分布更加集中．
故选：C．
【点评】本题主要考查茎叶图的应用，属于基础题．
4．（5分）来自澳大利亚的心理学家Michael White设计出了一种被人称为“怀特错觉”的光学戏法．这类型的图片只有三种颜色：黑、白、灰，但大多数人都会看到四种颜色．这是因为灰色的色块嵌入了白色和黑色条纹中，从视觉上看，在所调查的100名调查者中，有55人认为图中有4种颜色，而在被调查者所列举的颜色中，有40人没有提到白色（他们认为白色是背景颜色，不算在图片颜色之中），估计在人群中产生怀特错觉的概率约为（ ）
A．0.45B．0.55C．0.05D．0.95
【分析】根据这个调查结果，得到100人中产生产生怀特错觉的人数为55+40＝95人，由此能估计在人群中产生怀特错觉的概率．
【解答】解：在所调查的100名调查者中，有55人认为图中有4种颜色，
而在被调查者所列举的颜色中，有40人没有提到白色（他们认为白色是背景颜色，
根据这个调查结果，得到100人中产生产生怀特错觉的人数为：
55+40＝95，
由此估计在人群中产生怀特错觉的概率约为P＝＝0.95．
故选：D．
【点评】本题考查概率的运算，考查古典概型等基础知识，考查运算求解能力等数学核心素养，是基础题．
5．（5分）命题“存在实数x，使x＞1”的否定是（ ）
A．对任意实数x，都有x＞1
B．不存在实数x，使x≤1
C．对任意实数x，都有x≤1
D．存在实数x，使x≤1
【分析】根据存在命题（特称命题）否定的方法，可得结果是一个全称命题，结合已知易得答案．
【解答】解：∵命题“存在实数x，使x＞1”的否定是
“对任意实数x，都有x≤1”
故选：C．
【点评】本题以否定命题为载体考查了特称命题的否定，熟练掌握全（特）称命题的否定命题的格式和方法是解答的关键．
6．（5分）已知x，y的取值如下表所示：
如果y与x呈线性相关，且线性回归方程为，则b＝（ ）
A．B．C．D．
【分析】估计条件中所给的三组数据，求出样本中心点，因为所给的回归方程只有b需要求出，利用待定系数法求出b的值，得到结果．
【解答】解：∵线性回归方程为，
又∵线性回归方程过样本中心点，
，
∴回归方程过点（8，5）
∴5＝2b+，
∴b＝﹣
故选：A．
【点评】本题考查线性回归方程，考查样本中心点满足回归方程，考查待定系数法求字母系数，是一个基础题，这种题目一旦出现是一个必得分题目．
7．（5分）如图所示的算法框图思路源于我国古代数学名著《九章算术》中的“更相减相术”，执行该算法框图，若输入的a、b分别为36、96（ ）
A．0B．8C．12D．24
【分析】由循环结构的特点，先判断，再执行，分别计算出当前的a，b的值，即可得到结论．
【解答】解：由a＝36，b＝96，
由a＜b，则b变为96﹣36＝60，
由a＜b，则b变为60﹣36＝24，
由a＞b，则a变为36﹣24＝12，
由a＜b，则b变为24﹣12＝12，
由a＝b＝12，
则输出的a＝12．
故选：C．
【点评】本题考查算法和程序框图，主要考查循环结构的理解和运用，以及赋值语句的运用，属于基础题．
8．（5分）从单词“equatin”中选取5个不同的字母排成一排，含有q、u（其中q、u相连）的不同排法共有（ ）
A．120种B．480种C．720种D．960种
【分析】根据已知条件，结合捆绑法，以及分步乘法计数原理，即可求解．
【解答】解：单词“equatin”共有8个字母，且8个字母各不相同，
从中选取7个字母，含有q 种，
若q、u相连，并与其余4个字母排序为种，
故所求的不同排法共有种．
故选：D．
【点评】本题主要考查排列、组合及简单计数问题，属于基础题．
9．（5分）已知空间四边形OABC，M，N分别是OA，BC的中点，且＝，＝，＝，用，，为（ ）
A．++B．﹣+
C．﹣++D．﹣+﹣
【分析】如图所示，连接ON，AN，利用向量的中点公式可得＝（+）＝（+），＝（+），进而即可得出．
【解答】解：如图所示，连接ON，
则＝（+）＝（+），
＝（+）
＝（﹣6+）
＝（﹣7++）
＝﹣++，
所以＝（+）＝﹣++．
故选：C．
【点评】熟练掌握向量的运算法则、中点公式等是解题的关键．
10．（5分）希尔宾斯基三角形是一种分形，由波兰数学家希尔宾斯基在1915年提出，先作一个正三角形（即以原三角形各边的中点为顶点的三角形），然后在剩下的小三角形中又挖去一个“中心三角形”，我们用白色代表挖去的面积（我们称黑三角形为希尔宾斯基三角形）．在如图第3个大正三角形中随机取点，则落在黑色区域的概率为（ ）
A．B．C．D．
【分析】我们要根据已知条件，求出第3个大正三角形的面积，及黑色区域的面积，代入几何概型计算公式，即可求出答案．
【解答】解：由题意可知：每次挖去的面积为前一个三角形剩下面积的，不妨设第一个三角形的面积为8．
∴第三个三角形的面积为1；
则阴影部分的面积之为：
第3个大正三角形中随机取点，则落在黑色区域的概率：，
故选：B．
【点评】几何概型的概率估算公式中的“几何度量”，可以为线段长度、面积、体积等，而且这个“几何度量”只与“大小”有关，而与形状和位置无关．解决的步骤均为：求出满足条件A的基本事件对应的“几何度量”N（A），再求出总的基本事件对应的“几何度量”N，最后根据P＝求解．
11．（5分）已知抛物线C：y2＝8x焦点为F，A是C上一点，O为坐标原点，则|AF|＝（ ）
A．B．3C．D．4
【分析】根据已知条件，结合三角形的面积公式，求出A的纵坐标，再结合抛物线的定义，即可求解．
【解答】解：抛物线C：y2＝8x焦点为F，即p＝2，
则|OF|＝2，
设A（x，y），
△AOF的面积为2，
则，
∵A是C上一点，
∴3＝8x，解得x＝，
∴|AF|＝＝．
故选：A．
【点评】本题主要考查抛物线的定义，属于基础题．
12．（5分）若直线y＝x+b与曲线有公共点，则实数b的取值范围为（ ）
A．B．C．D．[﹣2，2]
【分析】直接利用直线与圆的位置关系求出点A和B的坐标，进一步求出参数b的取值范围．
【解答】解：直线y＝x+b与曲线有公共点，
如图所示：
利用曲线在坐标系中的位置，
所以A（6，2），B（8，
故实数b的取值范围为．
故选：A．
【点评】本题考查的知识要点：圆与直线的位置关系，主要考查学生的运算能力和数学思维能力，属于基础题．
13．（5分）已知函数f（x）＝则关于x的方程f2（x）+bf（x）+c＝0有5个不同实数解的充要条件是（ ）
A．b＜﹣2 且 c＞0B．b＞﹣2 且 c＜0
C．b＜﹣2 且 c＝0D．b≥﹣2 且 c＝0
【分析】作出f（x）的简图，数形结合可得．
【解答】解：∵方程f2（x）+af（x）+b＝0有且只有7个不同实数解，
∴对应于f（x）等于某个常数有4个不同实数解，
由题意作出f（x）的简图：
由图可知，只有当f（x）＝0时．
且f（x）＝﹣b时有四个根，
由图可知﹣b＞8，∴b＜﹣2．
故所求充要条件为：b＜﹣2且c＝3，
故选：C．
【点评】本题考查方程根的个数问题，数形结合是解决问题的关键，属中档题．
14．（5分）函数f（x）＝x2﹣2x，g（x）＝ax+2（a＞0），对∀x1∈[﹣1，2]，∃x0∈[﹣1，2]，使g（x1）＝f（x0），则a的取值范围是（ ）
A．B．C．[3，+∞）D．（0，3]
【分析】先求出两个函数在[﹣1，2]上的值域分别为A、B，再根据对任意的x1∈[﹣1，2]，存在x0∈[﹣1，2]，使g（x1）＝f（x0），集合B是集合A的子集，并列出不等式，解此不等式组即可求得实数a的取值范围，注意条件a＞0．
【解答】解：设f（x）＝x2﹣2x，g（x）＝ax+4（a＞0），2]上的值域分别为A、B，
由题意可知：A＝[﹣4，3]，2a+4]
∴
∴a≤
又∵a＞0，
∴8＜a≤
故选：A．
【点评】此题是个中档题．考查函数的值域，难点是题意的理解与转化，体现了转化的思想．同时也考查了同学们观察、推理以及创造性地分析问题、解决问题的能力，
二、填空题（共6小题，每小题5分，本题共20分．请把正确答案填在答题卡中相应题号的横线上）
15．（5分）某中学有高中生3500人，初中生1500人，为了解学生的学习情况，则应从高中生中抽取 70 人．
【分析】根据已知条件，结合分层抽样的定义，即可求解．
【解答】解：由题意可知，用分层抽样的方法从该校学生中抽取一个容量为100的样本，
则应从高中生中抽取＝70人．
故答案为：70．
【点评】本题主要考查分层抽样的定义，属于基础题．
16．（5分）的展开式中的常数项是： ﹣20 ．（请用数字作答）
【分析】先求出展开式的通项公式，令6﹣2r＝3，即可求解．
【解答】解：展开式的通项公式为Tr+8＝＝x4﹣2r，
令6﹣2r＝0，解得r＝3，
故的展开式中的常数项是．
故答案为：﹣20．
【点评】本题主要考查二项式定理，属于基础题．
17．（5分）圆x2+y2﹣2x﹣5＝0与圆x2+y2+2x﹣4y﹣4＝0的交点为A，B，则线段AB的垂直平分线方程为 x+y﹣1＝0 ．
【分析】线段AB的垂直平分线经过两圆的圆心，将圆的方程化为标准方程，求得圆心坐标，即可得到线段AB的垂直平分线方程；x2+y2﹣4x﹣5＝0与圆x2+y2﹣2x﹣4y﹣4＝0
【解答】解：线段AB的垂直平分线经过两圆的圆心
∵圆x2+y2﹣3x﹣5＝0可化为：（x﹣4）2+y2＝7，圆x2+y2+5x﹣4y﹣4＝4可化为：（x+1）2+（y﹣2）2＝9
∴两圆的圆心分别为（6，0），2）
∴线段AB的垂直平分线方程为，即x+y﹣7＝0
故答案为：x+y﹣1＝4．
【点评】本题以两圆相交为载体，考查两圆公共弦的方程，考查两圆公共弦的垂直平分线的方程，考查圆中的弦长，有一定的综合性．
18．（5分）在正方体ABCD﹣A1B1C1D1中，M，N分别为AD，C1D1的中点，O为侧面BCC1B1的中心，则异面直线MN与OD1所成角的余弦值为 ．
【分析】以A为坐标原点，AB为x轴，AD为y轴，AA1为z轴，建立空间直角坐标系，利用向量法能求出异面直线MN与OD1所成角的余弦值．
【解答】解：以A为坐标原点，AB为x轴，AA1为z轴，建立空间直角坐标系，
令AB＝2，则D6（0，2，5），1，1），8，0），2，2），
∴＝（1，1，＝（﹣2，1，
设异面直线MN与OD8所成角为θ，
则csθ＝＝．
∴异面直线MN与OD1所成角的余弦值为．
故答案为：．
【点评】本题考查异面直线所成角的余弦值的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，是基础题．
19．（5分）已知双曲线的左、右焦点分别为F1，F2，点P为双曲线C右支上一点，直线PF1与圆x2+y2＝a2相切，且∠F1PF2＝∠PF1F2，则双曲线C的离心率为 ．
【分析】过F2作F2M⊥PF1，垂足点为M，设切点为N，则根据题意易得M为PF1的中点，N为F1M的中点，又易知|F1N|＝b，从而可得，|PF1|＝4b，又易知|F2P|＝|F2F1|＝2c，从而可得|PF1|﹣|F2F1|＝4b﹣2c＝2a，再转化为e的方程，即可求解．
【解答】解：如图，∵∠F1PF2＝∠PF8F2，
∴|F2F6|＝|F2P|，过F2作F3M⊥PF1，垂足点为M，则M为PF1的中点，
设直线PF7与圆x2+y2＝a6相切的切点为N，则NO⊥PF1，
∴ON∥MF2，又O为F7F2的中点，
∴N为F1M的中点，
在Rt△F2NO中，根据题意易知|ON|＝a1O|＝c，
∴|F1N|＝b，∴|PF8|＝4|F1N|＝4b，
∴|PF1|﹣|PF2|＝2a，又|F2P|＝|F2F3|＝2c，
∴|PF1|﹣|F5F1|＝4b﹣5c＝2a，
∴2b＝a+c，
∴8b2＝（a+c）2，
∴5（c2﹣a2）＝（a+c）7，
∴3e2﹣6e﹣5＝0，又e＞7，
∴解得e＝，
故答案为：．
【点评】本题考查双曲线的几何性质，化归转化思想，数形结合思想，属中档题．
20．（5分）F1，F2分别是双曲线＝1的左、右焦点，P为双曲线右支上一点1F2的内心，且＝﹣λ，则λ＝ ．
【分析】设△PF1F2的内切圆半径为r，由|PF1|﹣|PF2|＝2a，|F1F2|＝2c，用△PF1F2的边长和r表示出等式中的三角形的面积，结合题中条件，即可解此等式求出λ．
【解答】解：设△PF1F2内切圆的半径为r，则＝﹣λ，
∴＝﹣
∴|PF1|﹣|PF2|＝λ|F1F2|，
根据双曲线的标准方程知3a＝λ•2c，
∴．
故答案为：．
【点评】本小题主要考查双曲线定义及标准方程的应用，考查学生转化问题的能力数数形结合数学思想的应用．
三、解答题（本大题共7小题，共70分．解答应写出文字说明、证明过程或演算步骤）
21．（10分）已知p：﹣2＜a＜2，q：关于x的方程x2﹣x+a＝0有实数根．
（1）若q为真命题，求实数a的取值范围；
（2）若p∨q为真命题，￢q为真命题，求实数a的取值范围．
【分析】（1）利用根的判别式能求出实数a的取值范围．
（2）p：﹣2＜a＜2，q：a．由p∨q为真命题，￢q为真命题，得到p是真命题，q是假命题，由此能求出实数a的取值范围．
【解答】解：（1）q：关于x的方程x2﹣x+a＝0有实数根．q为真命题，
∴Δ＝8﹣4a≥0，解得a．
∴实数a的取值范围是（﹣∞，]．
（2）p：﹣2＜a＜2，q：a．
∵p∨q为真命题，￢q为真命题，
∴p是真命题，q是假命题，
∴，
解得．
∴实数a的取值范围是（）．
【点评】本题考查实数的取值范围的求法，考查根的判别式、复合命题的真假判断等基础知识，考查运算求解能力，是基础题．
22．（10分）求解下列问题：
（1）求过直线x﹣y﹣5＝0与直线x+y﹣3＝0的交点，且与直线3x﹣4y+6＝0平行的直线方程；
（2）求以点（1，2）为圆心，与直线4x+3y﹣35＝0相切的圆的方程．
【分析】（1）根据交点直线系，直线平行的条件，方程思想，即可求解；
（2）根据点到直线的距离公式，即可求解．
【解答】解：（1）根据题可设所求直线方程为：
（x﹣y﹣5）+λ（x+y﹣3）＝7，
即（λ+1）x+（λ﹣1）y﹣（2+3λ）＝0，
又该直线与2x﹣4y+6＝6平行，
∴，
解得λ＝，
∴所求直线方程为3x﹣4y﹣16＝8；
（2）∵以点（1，2）为圆心的圆与直线7x+3y﹣35＝0相切，
则圆心（4，2）到直线4x+5y﹣35＝0的距离d＝，
∴所求圆的方程为（x﹣1）6+（y﹣2）2＝25．
【点评】本题考查交点直线系的应用，直线平行的条件，点到直线的距离公式的应用，方程思想，属中档题．
23．（10分）开学初学校进行了一次摸底考试，物理老师为了了解自己所教的班级参加本次考试的物理成绩的情况，从参考的本班同学中随机抽取n名学生的物理成绩（满分100分），将所得数据进行分析整理后画出频率分布直方图如图所示，已知抽取的学生中成绩在[50
（1）求n的值，并估计本班参考学生的平均成绩；
（2）已知抽取的n名参考学生中，在[90，100]的人中，现从[90，100]的人中随机抽取2人参加物理竞赛
【分析】（1）根据已知条件，结合频率分布直方图的性质，以及平均数公式，即可求解．
（2）根据已知条件，结合列举法和古典概型的概率公式，即可求解．
【解答】解：（1）由频率分布直方图知，成绩在[50，
因为成绩在[50，60）内的频数为3，
所以抽取的样本容量，
所以参考学生的平均成绩为55×0.075+65×0.2+75×0.4+85×5.125+95×0.1＝73.75（分）．
（2）由频率分布直方图知，抽取的学生中成绩在[90，
因为有甲、乙两名女生，
用A，B表示两名男生，甲A，乙A，AB，其中女学生甲被抽到的情况共5种，
所以随机抽取2人参加物理竞赛，其中女学生甲被抽到的概率为．
【点评】本题主要考查了频率分布直方图的性质，以及古典概型的概率公式，属于基础题．
24．（10分）某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系，他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数，得到如下资料：
（1）求出y关于x的线性回归方程；
（2）如果7月10号昼夜温差为8°C，预测因患感冒而就诊的人数（结果保留整数）．
附：回归方程中斜率和截距的最小二乘估计公式分别为：，．
【分析】（1）根据已知条件，结合最小二乘法公式，即可求解；
（2）将x＝8代入（1）所求的线性回归方程，即可求解．
【解答】解：（1）由表中数据可得，，，
＝1398，，
故＝＝，，
故y关于x的线性回归方程为＝3.95x+2.5；
（2）如果2月10号昼夜温差为8°C，即x＝8，
＝4.95×8+2.8＝18.1≈18，即因患感冒而就诊的人数约为18人．
【点评】本题主要考查线性回归方程的求解，属于基础题．
25．（10分）如图，四边形ABCD为正方形，E，F分别为AD，以DF为折痕把△DFC折起，使点C到达点P的位置
（1）证明：平面PEF⊥平面ABFD；
（2）求DP与平面ABFD所成角的正弦值．
【分析】（1）利用正方形的性质可得BF垂直于面PEF，然后利用平面与平面垂直的判断定理证明即可．
（2）利用等体积法可求出点P到面ABCD的距离，进而求出线面角．
【解答】（1）证明：由题意，点E、BC的中点，
则，，
由于四边形ABCD为正方形，所以EF⊥BC．
由于PF⊥BF，EF∩PF＝F．
又因为BF⊂平面ABFD，所以：平面PEF⊥平面ABFD．
（2）在平面PEF中，过P作PH⊥EF于点H，
由于EF为面ABCD和面PEF的交线，PH⊥EF，
则PH⊥面ABFD，故PH⊥DH．
在三棱锥P﹣DEF中，可以利用等体积法求PH，
因为DE∥BF且PF⊥BF，
所以PF⊥DE，
又因为△PDF≌△CDF，
所以∠FPD＝∠FCD＝90°，
所以PF⊥PD，
由于DE∩PD＝D，则PF⊥平面PDE，
故VF﹣PDE＝，
因为BF∥DA且BF⊥面PEF，
所以DA⊥面PEF，
所以DE⊥EP．
设正方形边长为2a，则PD＝2a
在△PDE中，，
所以，
故VF﹣PDE＝，
又因为，
所以PH＝＝，
所以在△PHD中，sin∠PDH＝＝，
即∠PDH为DP与平面ABFD所成角的正弦值为：．
【点评】本题主要考查点、直线、平面的位置关系．直线与平面所成角的求法．几何法的应用，考查转化思想以及计算能力．
26．（10分）已知椭圆C中心在坐标原点，焦点在x轴上，且过点P，B两点（A，B两点不是左右顶点），若直线l的斜率为时上．
（Ⅰ）求椭圆C的方程．
（Ⅱ）若以A，B两点为直径的圆过椭圆的右顶点，则直线l是否经过定点，求出定点坐标，若不是
【分析】（Ⅰ）设椭圆的标准方程为，A（x1，y1），B（x2，y2）利用平方差法求出a，b关系，利用椭圆经过的点，即可求出a，b，得到椭圆方程．
（Ⅱ）由题意可得椭圆右顶点A2（2，0），，通过（1）当直线l的斜率不存在时，设直线l的方程为x＝x0，求出直线l的方程．（2）当直线l的斜率存在时，设直线l的方程为y＝kx+b，推出①，联立直线和椭圆方程利用韦达定理的经过代入①求解即可．
【解答】解：（Ⅰ）设椭圆的标准方程为，A（x1，y1），B（x8，y2）
由题意得经过变换则有当时，，
再根据 得到a2＝2b2，又因为椭圆过得到a＝2，
所以椭圆的方程为：．
（Ⅱ）由题意可得椭圆右顶点A2（2，2），
（1）当直线l的斜率不存在时，设直线l的方程为x＝x0，
此时要使以A，B两点为直径的圆过椭圆的右顶点，
则，解得0＝7（舍），
此时直线l为．
（2）当直线l的斜率存在时，设直线l的方程为y＝kx+b5x2﹣2（x6+x2）+y1y4＝0，
化简得①
联立直线和椭圆方程得（4k2+8）x2+8kbx+8b2﹣4＝7，Δ＝1+4k7﹣b2＞0，
②
把②代入①得
即6k2b2﹣6k2+4b5﹣4﹣8k6b2+16kb＝﹣（4k2b2+16k2+b3+4），
12k2+16kb+5b2＝0，得k＝﹣或或（2
综上所述直线l过定点．
【点评】本题考查直线与椭圆的位置关系的综合应用，直线系方程的应用，考查分析问题解决问题的能力；分类讨论思想的应用．
27．（10分）已知椭圆，四个点P1（1，1），P2（0，1），，中恰有三点在椭圆C上．
（1）求椭圆C的方程；
（2）设直线l：y＝kx+m（m≠1）与椭圆C相交于A，B两点．若直线P2A与直线P2B的斜率的和为﹣1，判断直线l是否经过定点，若过定点；若不过定点，请说明理由．
【分析】（1）根据椭圆的对称性可知P3，P4两点在椭圆C上，即可得到，将点P1代入椭圆方程与比较，可得出点P2在椭圆C上，代入得到方程组，解出a，b的值，从而求出椭圆C的方程；
（2）设直线P2A与直线P2B的斜率分别为k1，k2，A（x1，y1），B（x2，y2），联立直线l与椭圆方程，根据韦达定理得出x1+x2，x1x2，根据已知k1+k2＝﹣1可求出k＝﹣，代入直线方程分离参数或根据直线点斜式即可得出直线所过定点．
【解答】解：（1）∵，关于y轴对称，
∴，两点在椭圆C上，
∴，
又，∴椭圆C不经过点P1，
∴点P4（0，1）在椭圆C上，
∴，解得，
∴椭圆C的方程为＝1；
（2）设直线P2A与直线P4B的斜率分别为k1，k2，
联立方程，消去y得2+1）x6+8kmx+4m6﹣4＝0，
设A（x7，y1），B（x2，y6），
∴x1+x2＝﹣，x1x2＝，
又∵k7+k2＝＝+＝＝﹣1，
∴（2k+3）x1x2+（m﹣8）（x1+x2）＝3，
即（2k+1）+（m﹣4），
解得k＝﹣，
∴直线l的方程为y＝﹣，即y+7＝﹣，
∴直线l过定点（6，﹣1）．
【点评】本题主要考查了椭圆的标准方程，考查了直线与椭圆的位置关系，以及直线过定点问题，属于中档题．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2023/12/11 23:20:17；用户：18086013149；邮箱：18086013149；学号：27613231x
2
3
4
y
6
4
5
日期
1月10日
2月10日
3月10日
4月10日
5月10日
6月10日
昼夜温差x（℃）
10
11
13
12
9
5
就诊人数y（人）
22
25
29
26
16
14
x
2
3
4
y
6
4
5
日期
1月10日
2月10日
3月10日
4月10日
5月10日
6月10日
昼夜温差x（℃）
10
11
13
12
9
5
就诊人数y（人）
22
25
29
26
16
14