2022-2023学年北京市清华附中高二（上）期末数学试卷

这是一份2022-2023学年北京市清华附中高二（上）期末数学试卷，共20页。试卷主要包含了解答题共6小题，共85分等内容，欢迎下载使用。

1．（4分）已知集合A＝{﹣2，﹣1，0，1，2}，B＝{x|﹣1＜x＜2}，则A∩B＝（ ）
A．{0，1}B．{﹣1，0，1}C．{0，1，2}D．{﹣1，0，1，2}
2．（4分）在复平面内，复数对应的点位于（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
3．（4分）双曲线的渐近线方程为（ ）
A．B．C．D．
4．（4分）设函数，则f（x）是（ ）
A．奇函数，且在（0，+∞）单调递增
B．奇函数，且在（0，+∞）单调递减
C．偶函数，且在（0，+∞）单调递增
D．偶函数，且在（0，+∞）单调递减
5．（4分）已知α，β是两个不同的平面，直线l⊂α，那么“α∥β”是“l∥β”的（ ）
A．充分而不必要条件
B．必要而不充分条件
C．充分必要条件
D．既不充分也不必要条件
6．（4分）已知函数的值域为R，则实数a的取值范围是（ ）
A．（﹣∞，0）B．（0，+∞）C．（﹣∞，1]D．[1，+∞）
7．（4分）点P在抛物线y2＝4x上，则P到直线x＝﹣1的距离与到直线3x﹣4y+12＝0的距离之和的最小值为（ ）
A．4B．3C．2D．1
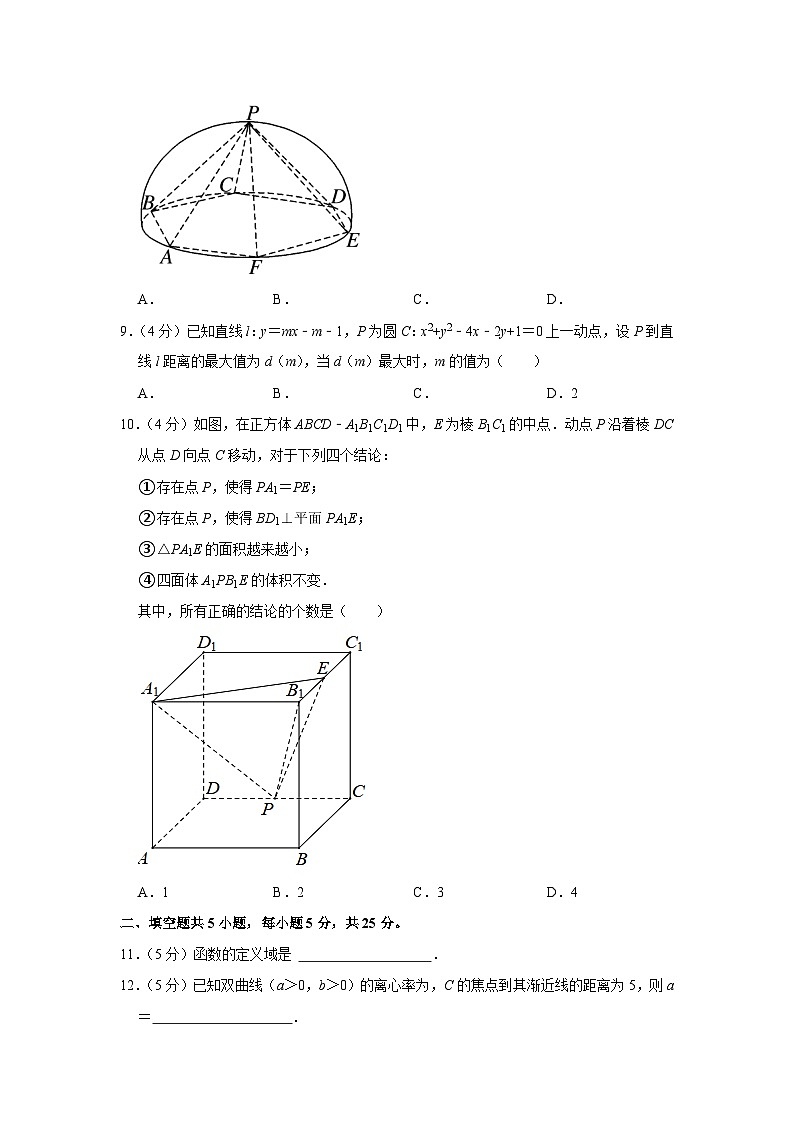
8．（4分）如图，半径为1的半球内有一内接正六棱锥P﹣ABCDEF，则异面直线PB与AF所成的角为（ ）
A．B．C．D．
9．（4分）已知直线l：y＝mx﹣m﹣1，P为圆C：x2+y2﹣4x﹣2y+1＝0上一动点，设P到直线l距离的最大值为d（m），当d（m）最大时，m的值为（ ）
A．B．C．D．2
10．（4分）如图，在正方体ABCD﹣A1B1C1D1中，E为棱B1C1的中点．动点P沿着棱DC从点D向点C移动，对于下列四个结论：
①存在点P，使得PA1＝PE；
②存在点P，使得BD1⊥平面PA1E；
③△PA1E的面积越来越小；
④四面体A1PB1E的体积不变．
其中，所有正确的结论的个数是（ ）
A．1B．2C．3D．4
二、填空题共5小题，每小题5分，共25分。
11．（5分）函数的定义域是 ．
12．（5分）已知双曲线（a＞0，b＞0）的离心率为，C的焦点到其渐近线的距离为5，则a＝ ．
13．（5分）若•2＝4，且||＝1，则||＝ ，•的最大值为 ．
14．（5分）已知等比数列{an}的各项均为正数，其前n项和为Sn，前n项乘积为Tn，T2＝T7，a6+a7＝6，则公比q＝ ；满足Sn＞Tn的正整数n的最大值为 ．
15．（5分）已知点P（2，0）和圆O：x2+y2＝36上两个不同的点M，N，满足∠MPN＝90°，Q是弦MN的中点，给出下列四个结论：
①|MP|的最小值是4；
②点Q的轨迹是一个圆；
③若点A（5，3），点B（5，5），则存在点Q，使得∠AQB＝90°；
④△MPN面积的最大值是．
其中所有正确结论的序号是 ．
三、解答题共6小题，共85分。解答应写出文字说明，演算步骤或证明过程。
16．（14分）已知函数f（x）＝4sinxcs的最大值与最小值之和为0．
（Ⅰ）求m的值以及f（x）的最小正周期；
（Ⅱ）若函数f（x）在区间[0，a]上是增函数，求实数a的最大值．
17．（14分）在△ABC中，角A，B，C所对的边分别为a，b，c，现有下列四个条件：
①；②cs；③a；④b＝2．
（Ⅰ）条件①和条件②可以同时成立吗？请说明理由；
（Ⅱ）请从上述四个条件中选择三个条件作为已知，使得△ABC存在且唯一，并求△ABC的面积．
18．（14分）如图，在三棱柱ABC﹣A1B1C1中，侧面AA1C1C⊥底面ABC，D为AC中点，AC＝AA1＝2，AB＝BC．
（Ⅰ）求证：B1C∥平面A1BD；
（Ⅱ）求证：平面BDA1⊥平面AA1C1C；
（Ⅲ）若，求三棱柱ABC﹣A1B1C1的体积．
19．（14分）已知函数．
（Ⅰ）求曲线y＝f（x）在点（1，f（1））处的切线方程；
（Ⅱ）求曲线y＝f（x）与直线y＝x﹣1的公共点个数，并说明理由；
（Ⅲ）若对于任意x∈（0，+∞），不等式f（x）＜ax+2恒成立，直接写出实数a的取值范围．
20．（14分）已知椭圆W：1（a＞b＞0）的离心率e，短轴长为2．
（Ⅰ）求椭圆W的标准方程；
（Ⅱ）设A为椭圆W的右顶点，C，D是y轴上关于x轴对称的两点，直线AC与椭圆W的另一个交点为B，点E为AB中点，点H在直线AD上且满足CH⊥OE（O为坐标原点），记△AEH，△ACD的面积分别为S1，S2，若，求直线AB的斜率．
21．（15分）已知无穷数列{an}满足：a1＝0，a2＝1，且当n≥3时，总存在i∈{1，2，⋯，n﹣1}，使得an．
（Ⅰ）求a4的所有可能值；
（Ⅱ）求a2023的所有可能值中的最大值；
（Ⅲ）求证：当n≥3时，an+1﹣an．
2022-2023学年北京市清华附中高二（上）期末数学试卷
参考答案与试题解析
一、选择题共10小题，每小题4分，共40分。在每小题列出的四个选项中，选出符合题目要求的一项。
1．（4分）已知集合A＝{﹣2，﹣1，0，1，2}，B＝{x|﹣1＜x＜2}，则A∩B＝（ ）
A．{0，1}B．{﹣1，0，1}C．{0，1，2}D．{﹣1，0，1，2}
【分析】利用交集定义求出A∩B．
【解答】解：集合A＝{﹣2，﹣1，0，1，2}，B＝{x|﹣1＜x＜2}，则A∩B＝{0，1}．
故选：A．
【点评】本题考查交集的求法，考查交集定义等基础知识，考查运算求解能力，是基础题．
2．（4分）在复平面内，复数对应的点位于（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【分析】把给出的复数运用复数的除法运算整理成a+bi（a，b∈R）的形式，得到复数的实部和虚部，则答案可求．
【解答】解：由．
知复数的实部为，虚部为．
所以，复数对应的点位于第二象限．
故选：B．
【点评】本题考查了复数代数形式的乘除运算，复数的除法，采用分子分母同时乘以分母的共轭复数，此题是基础题．
3．（4分）双曲线的渐近线方程为（ ）
A．B．C．D．
【分析】由双曲线的性质及方程直接可得双曲线的渐近线的方程．
【解答】解：由双曲线的方程可得渐近线方程为：yx，
故选：A．
【点评】本题考查双曲线的性质，渐近线方程的求法，属于基础题．
4．（4分）设函数，则f（x）是（ ）
A．奇函数，且在（0，+∞）单调递增
B．奇函数，且在（0，+∞）单调递减
C．偶函数，且在（0，+∞）单调递增
D．偶函数，且在（0，+∞）单调递减
【分析】根据函数奇偶性和单调性的定义进行判断即可．
【解答】解：函数的定义域为{x|x≠0}，
f（﹣x）＝﹣x3（x3）＝﹣f（x），则f（x）是奇函数，
当x＞0时，y＝x3和y是增函数，则f（x）在（0，+∞）上也是增函数，
故选：A．
【点评】本题主要考查函数奇偶性和单调性的判断，掌握函数奇偶性和单调性的定义和性质是解决本题的关键，是基础题．
5．（4分）已知α，β是两个不同的平面，直线l⊂α，那么“α∥β”是“l∥β”的（ ）
A．充分而不必要条件
B．必要而不充分条件
C．充分必要条件
D．既不充分也不必要条件
【分析】由题意分别判断充分性和必要性是否成立即．
【解答】解：若α∥β，则l与β没有交点，故l∥β，即充分性成立，
反之，若l∥β，有可能α，β相交，而l与交线平行，故必要性不成立，
综上可得，“α∥β”是“l∥β”的充分不必要条件．
故选：A．
【点评】本题主要考查线面之间的位置关系，充分性与必要性的判定等知识，属于基础题．
6．（4分）已知函数的值域为R，则实数a的取值范围是（ ）
A．（﹣∞，0）B．（0，+∞）C．（﹣∞，1]D．[1，+∞）
【分析】分别求函数在x＜0及x≥0时函数值的取值范围，结合题意知（﹣∞，0）∪[1﹣a，+∞）＝R，从而求实数a的取值范围．
【解答】解：①当x＜0时，
f（x）0，
即f（x）∈（﹣∞，0）；
②当x≥0时，
f（x）＝2x﹣a≥1﹣a，
即f（x）∈[1﹣a，+∞）；
∵函数的值域为R，
∴（﹣∞，0）∪[1﹣a，+∞）＝R，
故1﹣a≤0，
故a≥1；
故实数a的取值范围是[1，+∞），
故选：D．
【点评】本题考查了分段函数的性质的应用，应用了分类讨论的思想方法，属于中档题．
7．（4分）点P在抛物线y2＝4x上，则P到直线x＝﹣1的距离与到直线3x﹣4y+12＝0的距离之和的最小值为（ ）
A．4B．3C．2D．1
【分析】首先确定抛物线的准线方程，然后结合抛物线的定义等价转化即可求得最值．
【解答】解：∵x＝﹣1是抛物线y2＝4x的准线，
∴P到x＝﹣1的距离等于|PF|，
∵抛物线y2＝4x的焦点F（1，0），
∴过F作l1：3x﹣4y+12＝0的垂线和抛物线的交点就是P，
∴点P到直线3x﹣4y+12＝0的距离和到直线x＝﹣1的距离之和的最小值就是F（1，0）到直线3x﹣4y+12＝0的距离，
∴点 P到直线l1：x＝﹣1的距离与到直线l2：3 x﹣4 y+12＝0的距离之和的最小值为．
故选：B．
【点评】本题主要考查抛物线的定义及其应用，抛物线中的最值问题等知识，属于中等题．
8．（4分）如图，半径为1的半球内有一内接正六棱锥P﹣ABCDEF，则异面直线PB与AF所成的角为（ ）
A．B．C．D．
【分析】连接BE，作P作PO⊥平面ABCDEF，交BE于O，则BE∥AF，∠PBO是异面直线PB与AF所成的角（或所成角的补角），再由OB＝OP＝1，PO⊥BO，能求出异面直线PB与AF所成的角．
【解答】解：如图，半径为1的半球内有一内接正六棱锥P﹣ABCDEF，
连接BE，作P作PO⊥平面ABCDEF，交BE于O，
则BE∥AF，∴∠PBO是异面直线PB与AF所成的角（或所成角的补角），
∵OB＝OP＝1，PO⊥BO，∴∠PBO，
∴异面直线PB与AF所成的角为．
故选：C．
【点评】本题考查异面直线所成角的定义及求法，考查运算求解能力，是中档题．
9．（4分）已知直线l：y＝mx﹣m﹣1，P为圆C：x2+y2﹣4x﹣2y+1＝0上一动点，设P到直线l距离的最大值为d（m），当d（m）最大时，m的值为（ ）
A．B．C．D．2
【分析】先得出直线过定点A（1，﹣1），再求出圆心坐标，由圆的对称性以及斜率公式得出m的值．
【解答】解：因为l：y﹣（﹣1）＝m（x﹣1），所以直线l过定点A（1，﹣1），
圆C：x2+y2﹣4x﹣2y+1＝0可化为（x﹣2）2+（y﹣1）2＝4，
则圆心C（2，1），r＝2，
由圆的对称性可知，当AC⊥l时，P到直线l距离的最大，则．
故选：A．
【点评】本题考查直线与圆的位置关系，考查学生的运算能力，属于中档题．
10．（4分）如图，在正方体ABCD﹣A1B1C1D1中，E为棱B1C1的中点．动点P沿着棱DC从点D向点C移动，对于下列四个结论：
①存在点P，使得PA1＝PE；
②存在点P，使得BD1⊥平面PA1E；
③△PA1E的面积越来越小；
④四面体A1PB1E的体积不变．
其中，所有正确的结论的个数是（ ）
A．1B．2C．3D．4
【分析】对于①，设正方体棱长为1，DP＝x（0≤x≤1），求出，由，解得x，确定①正确；对于②，建立空间直角坐标系，利用向量法求出BD1与A1E不垂直，从而不存在点P，使得BD1⊥平面PA1E；对于③，利用向量法求解；对于④，由CD∥平面A1B1C1D1，P∈CD，得P到平面A1B1E的距离不变，再由△A1B1E的面积不变，得到四面体A1PB1E的体积不变．
【解答】解：对于①，设正方体棱长为1，DP＝x（0≤x≤1），
由AA1⊥平面ABCD，AP⊂平面ABCD，得AA1⊥AP，同理PC⊥EC，
∴2+x2，PE2＝PC2+CC12+C!E2＝1+（1﹣x）2，
由2+x2（1﹣x）2，解得x，∴存在点P，使得PA1＝PE，故①正确；
对于②，以D为坐标原点，建立空间直角坐标系，如图，
则B（1，1，0），D1（0，0，1），A1（1，0，1），E（，1，1），
（﹣1，﹣1，1），（，1，0），
∵，∴BD1与A1E不垂直，
∴不存在点P，使得BD1⊥平面PA1E，故②错误；
对于③，A1（1，0，1），E（，1，1），设P（0，m，0）（0≤m≤1），
PE，
（，1﹣m，1），（，1，0），
cs，
设P到直线A1E的距离为d，
则d＝||sin•，
由二次函数性质得0≤m≤1时，y＝（m﹣2）2+5单调递减，∴d单调递减，
∵A1E不变，∴△PA1E的面积越来越小，故③正确；
对于④，正方体ABCD﹣A1B1C1D1中，CD∥平面A1B1C1D1，P∈CD，
∴P到平面A1B1C1D1的距离不变，∴P到平面A1B1E的距离不变，
又△A1B1E的面积不变，∴四面体A1PB1E的体积不变，故④正确．
故选：C．
【点评】本题考查正方体结构特征、二次函数的性质、点到直线的距离、线面垂直的判定与性质、向量法等基础知识，考查运算求解能力，是中档题．
二、填空题共5小题，每小题5分，共25分。
11．（5分）函数的定义域是 {x|x≥﹣1且x≠0} ．
【分析】根据函数的解析式，列出使函数解析式有意义的不等式组，求出解集即可．
【解答】解：∵，
∴，∴x≥﹣1且x≠0，
∴函数的定义域是{x|x≥﹣1且x≠0}，
故答案为：{x|x≥﹣1且x≠0}．
【点评】本题考查了函数定义域的求法，解题的关键是列出使函数解析式有意义的不等式组，是基础题．
12．（5分）已知双曲线（a＞0，b＞0）的离心率为，C的焦点到其渐近线的距离为5，则a＝ ．
【分析】由双曲线的离心率公式，双曲线的渐近线方程，及点到直线的距离公式即可求得a即可．
【解答】解：由双曲线的离心率e，ca，
双曲线的渐近线方程l：y＝±x，焦点为F（c，0），
则焦点到渐近线的距离db＝5，
由c2＝a2+b2，解得：a2，所以a．
故答案为：．
【点评】本题考查双曲线的简单几何性质的应用，点到直线的距离公式的应用，是基础题．
13．（5分）若•2＝4，且||＝1，则||＝ 2 ，•的最大值为 ﹣2 ．
【分析】根据向量数量积定义及其运算性质计算，再根据余弦函数最值性求解．
【解答】解：因为2＝4，所以||＝2，
因为•（）••••4＝||•||•cs，4＝1•2•cs，4＝2cs，4≤﹣2，当，0时，等号成立．
所以•的最大值是﹣2，
故答案为：2；﹣2．
【点评】本题考查了平面向量数量积的性质及其运算，属于中档题．
14．（5分）已知等比数列{an}的各项均为正数，其前n项和为Sn，前n项乘积为Tn，T2＝T7，a6+a7＝6，则公比q＝ 2n﹣5，n∈N* ；满足Sn＞Tn的正整数n的最大值为 10 ．
【分析】分两种情况：当公比为1时，当公比不为1时，进行讨论T2＝T7，a6+a7＝6，列方程求出首项和公比，即可求出Sn，Tn，根据Sn＞Tn，转化为二次不等式，即可得出答案．
【解答】解：当公比为1时，由T2＝T7，得a12＝a17，
所以a1＝1，
所以a6+a7＝2，与题意矛盾，不成立，
当公比不为1时，设公比为q，
由T2＝T7，得a1a2＝a1a2a3a4a5a6a7，
所以a12q＝a17q21，
所以a15q20＝1，①
所以a6+a7＝a1q5（1+q）＝6，②
由①②得，q5（1+q）5＝65，
解得q＝2或q＝﹣3（舍），
所以q＝2，
代入②得a1＝2﹣4，
所以Sn，
所以Tn＝2﹣4+（﹣3）+...+（n﹣5）＝2，
若Sn＞Tn，则2，
所以2n﹣1＞2，
所以2n﹣21，
所以只需n，即n2﹣11n+8＜0，
解得n，
所以满足Sn＞Tn的最大正整数n的值为10，
故答案为：2n﹣5，n∈N*；10．
【点评】本题考查等比数列的性质，解题中需要理清思路，属于中档题．
15．（5分）已知点P（2，0）和圆O：x2+y2＝36上两个不同的点M，N，满足∠MPN＝90°，Q是弦MN的中点，给出下列四个结论：
①|MP|的最小值是4；
②点Q的轨迹是一个圆；
③若点A（5，3），点B（5，5），则存在点Q，使得∠AQB＝90°；
④△MPN面积的最大值是．
其中所有正确结论的序号是 ①②④ ．
【分析】①可以通过设出圆的参数方程，进行求解；②设出Q（x，y），找到等量关系，建立方程，求出点Q的轨迹方程，即可说明；③转化为两圆是否有交点，说明是否存在点Q；④当PM，PN斜率分别为1和﹣1时，且点P，M在y轴左侧，此时△MPN 面积最大，求出最大值．
【解答】解：点M在圆O：x2+y2＝36上，设M（6csθ，6sinθ），则，
当csθ＝1时，|MP|取得最小值，最小值为4，①正确；
设点Q（x，y），则由题意得PQ2＝QM2＝OM2﹣OQ2，
则（x﹣2）2+y2＝36﹣（x2+y2），
整理得：（x﹣1）2+y2＝17，
所以点Q的轨迹是一个圆，②正确；
以AB为直径的圆，圆心为（5，4），半径为1，
方程为：（x﹣5）2+（y﹣4）2＝1，
下面判断此圆与点Q的轨迹方程（x﹣1）2+y2＝17是否有交点，
由于，两圆相离，
故不存在点Q，使得∠AQB＝90°，③错误；
当PM，PN斜率分别为1和﹣1时，且点P，M在y轴左侧，此时△MPN为等腰直角三角形，面积最大，
此时，④正确．
故答案为：①②④．
【点评】本题考查了轨迹方程问题，属于中档题．
三、解答题共6小题，共85分。解答应写出文字说明，演算步骤或证明过程。
16．（14分）已知函数f（x）＝4sinxcs的最大值与最小值之和为0．
（Ⅰ）求m的值以及f（x）的最小正周期；
（Ⅱ）若函数f（x）在区间[0，a]上是增函数，求实数a的最大值．
【分析】（Ⅰ）根据三角恒等变换公式化简可得f（x）＝2sin（2x）m，结合正弦函数的最值与已知条件，可得m的值，得解；
（Ⅱ）根据正弦函数的单调性，即可得解．
【解答】解：（Ⅰ）f（x）＝4sinxcs4sinx（csxsinx）+m＝2sinxcsx+2sin2x+m＝sin2x•（1﹣cs2x）+m＝2sin（2x）m，
所以f（x）的最大值为2m，最小值为﹣2m，
由题意知，（2m）+（﹣2m）＝0，解得m，
所以f（x）＝2sin（2x），
所以f（x）的最小正周期为Tπ，
综上，m，最小正周期为π．
（Ⅱ）令2x∈[2kπ，2kπ]，k∈Z，则x∈[kπ，kπ]，k∈Z，
当k＝0时，f（x）在[，]上单调递增，
因为函数f（x）在区间[0，a]上是增函数，
所以a，即实数a的最大值为．
【点评】本题考查三角函数的综合应用，熟练掌握正弦函数的图象与性质，三角恒等变换公式是解题的关键，考查逻辑推理能力和运算能力，属于中档题．
17．（14分）在△ABC中，角A，B，C所对的边分别为a，b，c，现有下列四个条件：
①；②cs；③a；④b＝2．
（Ⅰ）条件①和条件②可以同时成立吗？请说明理由；
（Ⅱ）请从上述四个条件中选择三个条件作为已知，使得△ABC存在且唯一，并求△ABC的面积．
【分析】（Ⅰ）分别推导出①成立以及②成立时的结论，再结合三角形的内角和定理即可作出判断；
（Ⅱ）若选条件①③④，先求得sinB，再由正弦定理求得sinA，根据和角公式求得sinC，最后由三角形的面积公式得解；
若选条件②③④，先由正弦定理求得sinB，进而得到B，C，再由三角形的面积公式得解．
【解答】解：（Ⅰ）若条件①成立，则，即，
又，B为△ABC的内角，
所以；
若条件②成立，则，
又A为△ABC的内角，则；
若条件①②同时成立，则此时A+B＞π，不合题意，
所以条件①和条件②不可能同时成立；
（Ⅱ）若选条件①③④，
由（Ⅰ）可知，，，
则，
由正弦定理可得，，则，
又，则，
所以，
所以；
若选条件②③④，
由（Ⅰ）可知，，
则由正弦定理可得，，则，
又B为△ABC的内角，则，
所以△ABC为直角三角形，且，
所以．
【点评】本题考查三角恒等变换以及正余弦定理，三角形的面积公式在解三角形中的运用，考查运算求解能力，属于中档题．
18．（14分）如图，在三棱柱ABC﹣A1B1C1中，侧面AA1C1C⊥底面ABC，D为AC中点，AC＝AA1＝2，AB＝BC．
（Ⅰ）求证：B1C∥平面A1BD；
（Ⅱ）求证：平面BDA1⊥平面AA1C1C；
（Ⅲ）若，求三棱柱ABC﹣A1B1C1的体积．
【分析】（Ⅰ）取A1C1中点E，连接B1E，CE，则B1E∥BD，CE∥A1D，从而平面A1BD∥平面CB1E，由此能证明B1C∥平面A1BD；
（Ⅱ）推导出BD⊥AC，从而BD⊥平面AA1C1C，由此能证明平面BDA1⊥平面AA1C1C；
（Ⅲ）求出BD＝B1E，从而A1D＝CE，由勾股定理得A1A⊥AC，从而A1D⊥平面ABC，由此能求出三棱柱ABC﹣A1B1C1的体积．
【解答】解：（Ⅰ）证明：在三棱柱ABC﹣A1B1C1中，侧面AA1C1C⊥底面ABC，
D为AC中点，AC＝AA1＝2，AB＝BC，
取A1C1中点E，连接B1E，CE，
则B1E∥BD，CE∥A1D，
∵B1E∩CE＝E，BD∩A1D＝D，
∴平面A1BD∥平面CB1E，
∵B1C⊂平面CB1D，∴B1C∥平面A1BD；
（Ⅱ）证明：∵D为AC中点，AB＝BC，
∴BD⊥AC，
∵侧面AA1C1C⊥底面ABC，侧面AA1C1C∩底面ABC＝AC，
∴BD⊥平面AA1C1C，
∵BD⊂平面BDA1，∴平面BDA1⊥平面AA1C1C；
（Ⅲ）∵侧面AA1C1C⊥底面ABC，D为AC中点，AC＝AA1＝2，AB＝BC．
∴BD＝B1E，
∵，∴A1D＝CE，
∴AD2+A1D2＝AA12，∴A1A⊥AC，
∵侧面AA1C1C⊥底面ABC，侧面AA1C1C∩底面ABC＝AC，
∴A1D⊥平面ABC，
∴三棱柱ABC﹣A1B1C1的体积为：
V＝S△ABC•A1D．
【点评】本题考查面面平行、线面平行、线面垂直的判定与性质、面面垂直的性质、勾股定理、三棱柱体积公式等基础知识，考查运算求解能力，是中档题．
19．（14分）已知函数．
（Ⅰ）求曲线y＝f（x）在点（1，f（1））处的切线方程；
（Ⅱ）求曲线y＝f（x）与直线y＝x﹣1的公共点个数，并说明理由；
（Ⅲ）若对于任意x∈（0，+∞），不等式f（x）＜ax+2恒成立，直接写出实数a的取值范围．
【分析】（Ⅰ）求出x＝1时的函数值，导数值，再利用点斜式求出切线；
（Ⅱ）转化为lnx＝x2﹣x根的个数，构造函数g（x）＝lnx﹣2+x，x＞0，研究其单调性、极值情况即可；
（Ⅲ）分离参数a，然后研究函数的最值即可．
【解答】解：x＞0，，
（Ⅰ）f（1）＝0，f′（1）＝1，故切线为y＝x﹣1；
（Ⅱ）只有一个公共点，理由：
由题意得，即lnx﹣x2+x＝0，
令g（x）＝lnx﹣x2+x，x＞0，g′（x）＝﹣（x﹣1）（2x+1），
0＜x＜1时，g′（x）＞0，x＞1时，g′（x）＜0，
故g（x）在（0，1）上递增，在（1，+∞）上递减，故g（x）max＝g（1）＝0，
所以g（x）只有一个零点1，即曲线y＝f（x）与直线y＝x﹣1只有一个公共点；
（Ⅲ）x∈（0，+∞），不等式f（x）＜ax+2恒成立，
可化为ax，即a，
令g（x），x＞0，g′（x），
再令φ（x）＝2x﹣2lnx+1，x＞0，，
0＜x＜1时，φ′（x）＜0，x＞1时，φ′（x）＞0，
故φ（1）＝3是φ（x）的极小值，也是最小值，故g′（x）＞0恒成立，
即g（x）在（0，+∞）上是增函数，而0＝0﹣0＝0，
故a≥0即为所求，
所以a的取值范围是[0，+∞）．
【点评】本题考查导数的几何意义，利用导数研究函数的单调性、极值与最值，进而解决不等式恒成立问题、函数的零点问题等，属于较难的题目．
20．（14分）已知椭圆W：1（a＞b＞0）的离心率e，短轴长为2．
（Ⅰ）求椭圆W的标准方程；
（Ⅱ）设A为椭圆W的右顶点，C，D是y轴上关于x轴对称的两点，直线AC与椭圆W的另一个交点为B，点E为AB中点，点H在直线AD上且满足CH⊥OE（O为坐标原点），记△AEH，△ACD的面积分别为S1，S2，若，求直线AB的斜率．
【分析】（Ⅰ）由椭圆的离心率和短轴长，结合a，b，c的关系，解得a，b，可得椭圆方程；
（Ⅱ）设出直线AC的方程，与椭圆方程联立，运用弦长公式可得|AB|，|AE|，由中点坐标公式可得E的坐标，进而得到直线CH的方程，与直线AD方程联立，求得H的坐标，再求H到直线AC的距离，由三角形的面积公式，解方程可得所求值．
【解答】解：（Ⅰ）离心率e，短轴长为2，可得b＝1，，
又a2＝b2+c2，
解得a＝2，c，则椭圆的方程为y2＝1；
（Ⅱ）可设C（0，t），D（0，﹣t），又A（2，0），可得直线AC的方程为y（x﹣2），
AD的方程为y（x﹣2），
联立可得（1+t2）x2﹣4t2x+4t2﹣4＝0，
Δ＝16t4﹣16（1+t2）（t2﹣1）＞0，
可得x1+x2，x1x2，则E（，），
kOE，则直线CH的方程为y＝﹣2tx+t，
联立，可得H（，t），
H到直线AC的距离为d．
又|AB|•，
可得|AE|，
所以S1••，
又S2•2|t|•2＝2|t|，，
所以，解得t＝±2，
则直线AB的斜率为±1．
【点评】本题考查椭圆的方程和性质，以及直线和椭圆的位置关系，考查方程思想和运算能力，属于中档题．
21．（15分）已知无穷数列{an}满足：a1＝0，a2＝1，且当n≥3时，总存在i∈{1，2，⋯，n﹣1}，使得an．
（Ⅰ）求a4的所有可能值；
（Ⅱ）求a2023的所有可能值中的最大值；
（Ⅲ）求证：当n≥3时，an+1﹣an．
【分析】（Ⅰ）推导出a1＝0，a2＝1，从而a3＝1或a3，由此能求出a4的所有可能值；
（Ⅱ）构造：当a1＝0，a2＝a3＝•••＝a2023＝1时，符合题设条件，可以取到．利用反证法证明：∀n≥3，均有an≤1恒成立．由此能求出a2023的最大值．
（Ⅲ）证明引理：∀k≥3，均有ak，利用数学归纳法和放缩法能证明当n≥3时，an+1﹣an．
【解答】解：（Ⅰ）无穷数列{an}满足：a1＝0，a2＝1，
当n≥3时，总存在i∈{1，2，⋯，n﹣1}，使得an，
∴a1＝0，a2＝1，∴a3＝1或a3，
当a3＝1时，a4＝1或a4；
当a3时，或，
∴a4的所有可能值为，1；
（Ⅱ）构造：当a1＝0，a2＝a3＝•••＝a2023＝1时，符合题设条件，可以取到．
下面证明：∀n≥3，均有an≤1恒成立．
（反证法）假设存在n0≥3，使得1，不妨设an是首个大于1的项，
则对于任意的1≤n＜n0，都有an≤1，
，则，i＝1，2，•••，n0﹣1，
∴对于任意的i∈{1，2，•••，n0﹣1}，都有，
这与已知条件矛盾，∴a2023的最大值为1．
（Ⅲ）证明：首先证明引理：∀k≥3，均有ak，①
当k＝3时，a3＝1或，引理成立．
②假设对于k＝3，4，•••，n﹣1，ak成立，
下证当k＝n（n≥4）时，有（*），
由{an}定义知：存在i∈{1，2，•••，n﹣1}，使得an（*），
若i＝1，2，则（*）式成立，
若3≤i≤n﹣1，先证明（*）式左边一半，则只需证明，
∴（n﹣1）（ai+ai+1+•••+an﹣1）≥（n﹣i）（a1+a2+•••+an﹣1），
∴（i﹣1）（ai+ai+1+•••+an﹣1）≥（n﹣i）（a1+a2+•••+ai﹣1），
∴，（**）
根据归纳假设，对于k＝3，4，•••，n﹣1，均有，
∴，
∴，
∴，•••，
依此类推，可得ai，ai﹣1，•••，an﹣1中每一项都大于等于，
∴ai，ai+1，•••，an﹣1的平均数也大于等于，故（**）式成立，
再证（*）式右边一半，同理只需证，
即应该和（***），
根据归纳假设可得ai，
∴
，


，故（***）式成立，
回到原题，利用引理和an≤1，可得：
an+1﹣anan
，
∴当n≥3时，an+1﹣an．
【点评】本题考查数列不等式的性质、放缩法、数列递推式、反证法、数学归纳法等基础知识，考查运算求解能力，是难题．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2023/12/8 10:25:36；用户：18086013149；邮箱：18086013149；学号：27613231