新高考数学二轮复习考点突破学案4.2《空间点、直线、平面之间的位置关系》（2份打包，原卷版+教师版）

这是一份新高考数学二轮复习考点突破学案4.2《空间点、直线、平面之间的位置关系》（2份打包，原卷版+教师版），文件包含新高考数学二轮复习考点突破学案42《空间点直线平面之间的位置关系》原卷版doc、新高考数学二轮复习考点突破学案42《空间点直线平面之间的位置关系》原卷版pdf、新高考数学二轮复习考点突破学案42《空间点直线平面之间的位置关系》教师版doc、新高考数学二轮复习考点突破学案42《空间点直线平面之间的位置关系》教师版pdf等4份试卷配套教学资源，其中试卷共49页， 欢迎下载使用。


考点一 空间直线、平面位置关系的判定
核心提炼
判断空间直线、平面位置关系的常用方法
(1)根据空间线面平行、垂直的判定定理和性质定理逐项判断，解决问题.
(2)必要时可以借助空间几何模型，如从长方体、四面体等模型中观察线、面的位置关系，并结合有关定理进行判断.
例1 (1)(多选)已知m，n是两条不同的直线，α，β是两个不同的平面，则下列说法正确的是( )
A.若α∥β，m⊂α，n⊂β，则m∥n B.若m⊥α，m∥n，n⊥β，则α∥β
C.若α⊥β，m⊂α，n⊂β，则m⊥n D.若m⊥α，m∥n，n∥β，则α⊥β
(2)(多选)每个面均为正三角形的八面体称为正八面体，如图.若点G，H，M，N分别是正八面体ABCDEF的棱DE，BC，AD，BF的中点，则下列结论正确的是( )
A.四边形AECF是平行四边形 B.GH与MN是异面直线
C.GH∥平面EAB D.GH⊥BC
规律方法 对于线面关系的存在性问题，一般先假设存在，然后再在该假设条件下，利用线面位置关系的相关定理、性质进行推理论证，寻找假设满足的条件，若满足，则假设成立；若得出矛盾，则假设不成立.
跟踪演练1 (1)(多选)在长方体ABCD﹣A1B1C1D1中，直线A1C与平面AB1D1的交点为M，O为线段B1D1的中点，则下列结论正确的是( )
A.A，M，O三点共线 B.M，O，A1，A四点共面
C.B，B1，O，M四点共面 D.A，O，C，M四点共面
(2)设点E为正方形ABCD的中心，M为平面ABCD外一点，△MAB为等腰直角三角形，且∠MAB＝90°，若F是线段MB的中点，则( )
A.ME≠DF，且直线ME，DF是相交直线
B.ME＝DF，且直线ME，DF是相交直线
C.ME≠DF，且直线ME，DF是异面直线
D.ME＝DF，且直线ME，DF是异面直线
考点二 空间平行、垂直关系
核心提炼
平行关系及垂直关系的转化
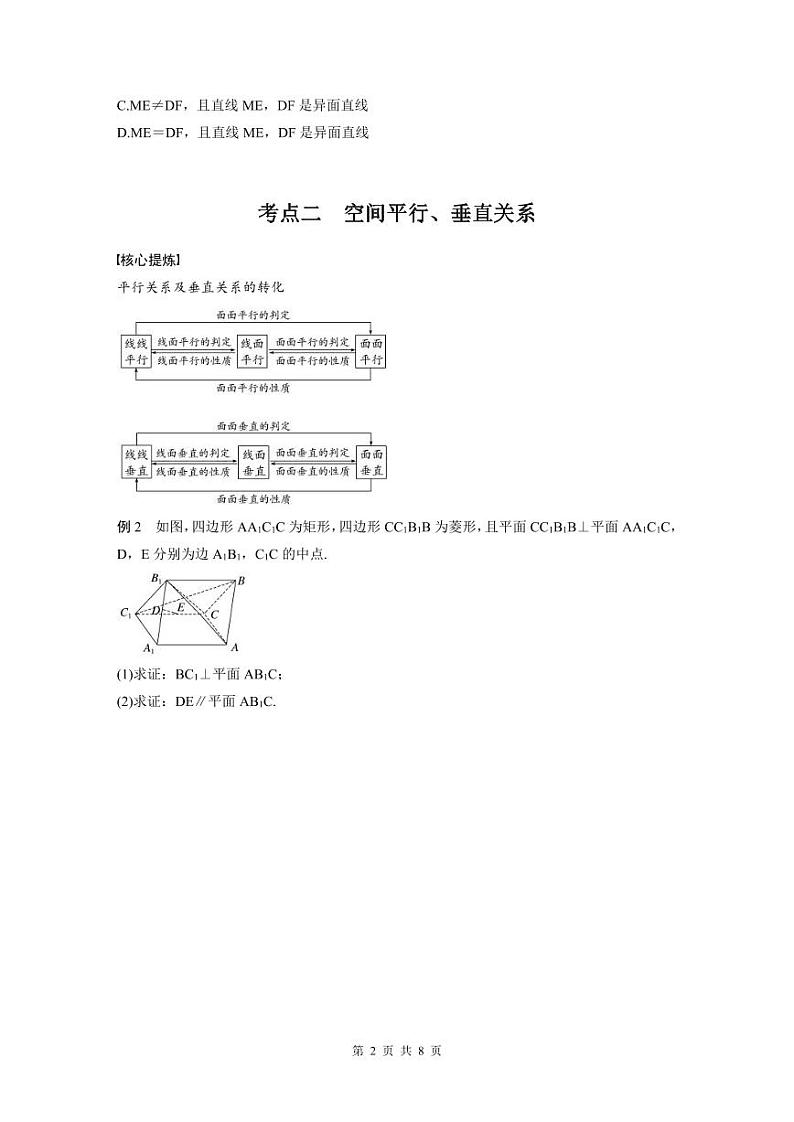
例2 如图，四边形AA1C1C为矩形，四边形CC1B1B为菱形，且平面CC1B1B⊥平面AA1C1C，D，E分别为边A1B1，C1C的中点.
(1)求证：BC1⊥平面AB1C；
(2)求证：DE∥平面AB1C.
规律方法 (1)证明线线平行的常用方法
①三角形的中位线定理；②平行公理；③线面平行的性质定理；④面面平行的性质定理.
(2)证明线线垂直的常用方法
①等腰三角形三线合一；②勾股定理的逆定理；③利用线面垂直的性质证线线垂直.
跟踪演练2 如图，在直三棱柱ABC﹣A1B1C1中，M，N分别是线段A1B，AC1的中点.
(1)求证：MN⊥AA1；
(2)在线段BC1上是否存在一点P，使得平面MNP∥平面ABC？若存在，指出点P的具体位置；若不存在，请说明理由.
考点三 翻折问题
核心提炼
翻折问题，关键是分清翻折前后图形的位置和数量关系的变与不变，一般地，位于“折痕”同侧的点、线、面之间的位置和数量关系不变，而位于“折痕”两侧的点、线、面之间的位置关系会发生变化；对于不变的关系应在平面图形中处理，而对于变化的关系则要在立体图形中解决.
例3 (1)已知正方形ABCD中E为AB中点，H为AD中点，F，G分别为BC，CD上的点，CF＝2FB，CG＝2GD，将△ABD沿着BD翻折得到空间四边形A1BCD，则在翻折过程中，以下说法正确的是( )
A.EF∥GH B.EF与GH相交 C.EF与GH异面 D.EH与FG异面
(2)(多选)如图，在矩形ABCD中，AB＝2AD，E为边AB的中点，将△ADE沿直线DE翻折成△A1DE.若M为线段A1C的中点，则在△ADE翻折的过程中，下面四个命题中正确的是( )
A.BM的长是定值
B.点M的运动轨迹在某个圆周上
C.存在某个位置，使DE⊥A1C
D.A1不在底面BCD上时，MB∥平面A1DE
易错提醒 注意图形翻折前后变与不变的量以及位置关系.对照前后图形，弄清楚变与不变的元素后，再立足于不变的元素的位置关系与数量关系去探求变化后的元素在空间中的位置与数量关系.
跟踪演练3 (多选)如图，在矩形ABCD中，BC＝1，AB＝x，BD和AC交于点O，将△BAD沿直线BD翻折，则下列说法中正确的是( )
A.存在x，在翻折过程中存在某个位置，使得AB⊥OC
B.存在x，在翻折过程中存在某个位置，使得AC⊥BD
C.存在x，在翻折过程中存在某个位置，使得AB⊥平面ACD
D.存在x，在翻折过程中存在某个位置，使得AC⊥平面ABD
专题强化练
一、单项选择题
1.已知三条直线a，b，c，若a和b是异面直线，b和c是异面直线，那么直线a和c的位置关系是( )
A.平行 B.相交 C.异面 D.平行、相交或异面
2.设α，β为两个不同的平面，则α∥β的一个充要条件可以是( )
A.α内有无数条直线与β平行
B.α，β垂直于同一个平面
C.α，β平行于同一条直线
D.α，β垂直于同一条直线
3.正方体上的点M，N，P，Q是其所在棱的中点，则下列各图中直线MN与直线PQ是异面直线的图形是( )
4.如图，在正方体ABCD﹣A1B1C1D1中，P是A1D的中点，则下列说法正确的是( )
A.直线PB与直线D1C平行，直线PB⊥平面A1C1D
B.直线PB与直线AC异面，直线PB⊥平面ADC1B1
C.直线PB与直线B1D1相交，直线PB⊂平面ABC1
D.直线PB与直线A1D垂直，直线PB∥平面B1D1C
5.如图，在四边形ABCD中，AD∥BC，AD＝AB，∠BCD＝45°，∠BAD＝90°，将△ABD沿BD折起，使平面ABD⊥平面BCD，构成三棱锥A﹣BCD，则在三棱锥A﹣BCD中，下列结论正确的是( )
A.平面ABD⊥平面ABC
B.平面ADC⊥平面BDC
C.平面ABC⊥平面BDC
D.平面ADC⊥平面ABC
6.如图，在棱长为2的正方体ABCD﹣A1B1C1D1中，过A1B且与AC1平行的平面交B1C1于点P，则PC1等于( )
A.2 B.eq \r(3) C.eq \r(2) D.1
二、多项选择题
7.如图，在空间四边形ABCD中，E，F分别为AB，AD的中点，G，H分别在BC，CD上，且BG∶GC＝DH∶HC＝1∶2，则( )
A.BD∥平面EGHF B.FH∥平面ABC
C.AC∥平面EGHF D.直线GE，HF，AC交于一点
8.如图1，已知E为正方形ABCD的边AB的中点，将△DAE沿边DE翻折到△PDE，连接PC，PB，EC，设F为PC的中点，连接BF，如图2，则在翻折的过程中，下列命题正确的是( )
A.存在某一翻折位置，使得DE∥平面PBC
B.在翻折的过程中(点P不在平面BCDE内)，都有BF∥平面PDE
C.存在某一翻折位置，使得PE⊥CD
D.若PD＝CD＝PC＝4，则三棱锥P﹣CDE的外接球的表面积为eq \f(76π,3)
三、填空题
9.已知l是平面α，β外的直线，给出下列三个论断：①l∥α；②α⊥β；③l⊥β.以其中两个论断为条件，余下的论断为结论，写出一个正确命题：________.(用序号表示)
10.三棱锥A﹣BCD中，AB＝CD＝1，过线段BC的中点E作平面EFGH与直线AB，CD都平行，且分别交BD，AD，AC于F，G，H，则四边形EFGH的周长为________.
11.已知三棱台ABC﹣A1B1C1的上、下底面均为正三角形，AB＝1，A1B1＝2，侧棱长AA1＝BB1＝CC1，若AA1⊥BB1，则此棱台的高为________.
12.如图，把边长为a的正方形ABCD沿对角线BD折起，使A，C的距离为a，则异面直线AC与BD的距离为________.
四、解答题
13.如图，四面体ABCD中，AD⊥CD，AD＝CD，∠ADB＝∠BDC，E为AC的中点.
(1)证明：平面BED⊥平面ACD；
(2)设AB＝BD＝2，∠ACB＝60°，点F在BD上，当△AFC的面积最小时，求三棱锥F﹣ABC的体积.
14.在直角梯形ABCD中，AD∥BC，A＝eq \f(π,2)，AD＝1，AB＝2，BC＝3，将梯形沿中位线EF折起使AE⊥BE，并连接AB，DC得到多面体AEB﹣DFC，连接DE，BD，BF.
(1)求证：DF⊥平面BED；
(2)求点E到平面BDF的距离.