河北省张家口桥东区五校联考2023-2024学年八年级数学第一学期期末统考模拟试题含答案

这是一份河北省张家口桥东区五校联考2023-2024学年八年级数学第一学期期末统考模拟试题含答案，共7页。试卷主要包含了下列语句是命题的是，若，则下列结论正确的是，下列各数中无理数是等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
请考生注意：
1．请用2B铅笔将选择题答案涂填在答题纸相应位置上，请用0．5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2．答题前，认真阅读答题纸上的《注意事项》，按规定答题。
一、选择题(每小题3分,共30分)
1．下列三条线段中，能构成三角形的是（ ）
A．3，4，8B．5、6，7C．5，5，10D．5，6，11
2．如图，已知点A、D、C、F在同一条直线上，AB＝DE，∠A＝∠EDF，再添加一个条件，可使△ABC ≌ △DEF，下列条件不符合的是
A．∠B＝∠EB．BC∥EFC．AD＝CFD．AD＝DC
3．一副三角板按如图方式摆放，且∠1的度数比∠2的度数大50°，若设∠1=x°，∠2=y°，则可得到方程组为
A．B．C．D．
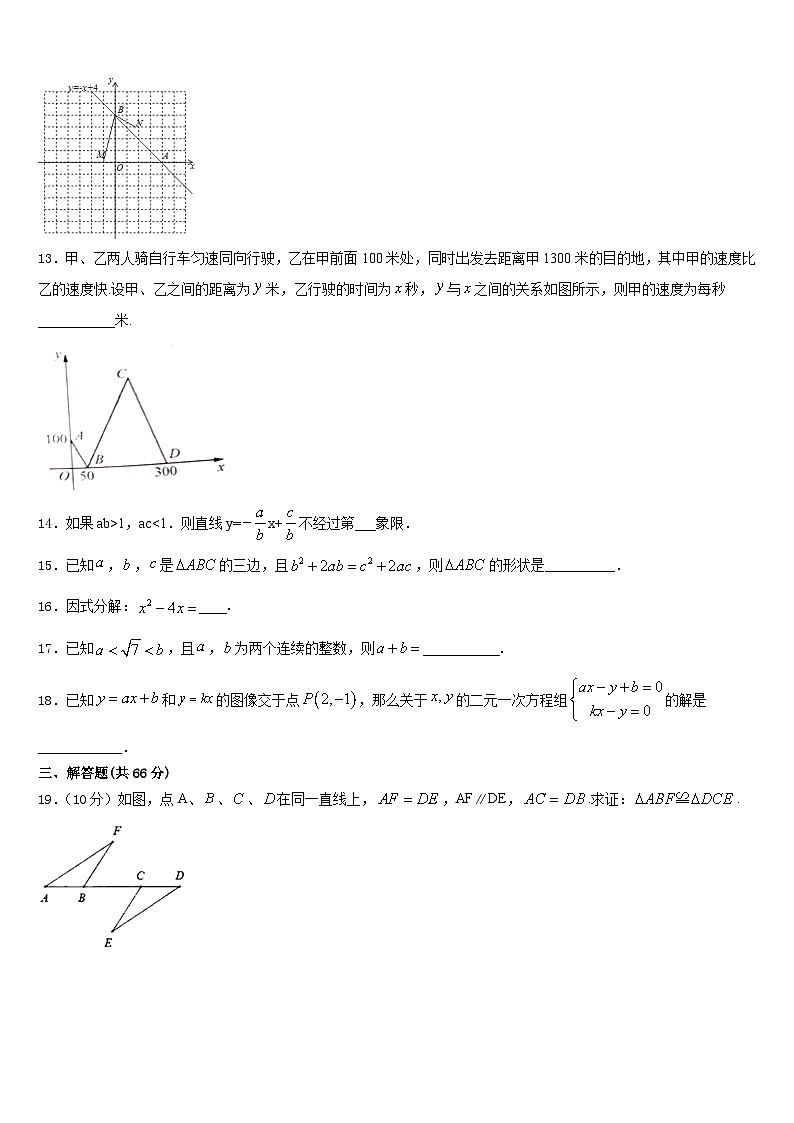
4．下列语句是命题的是（ ）
（1）两点之间，线段最短；
（2）如果两个角的和是90度，那么这两个角互余.
（3）请画出两条互相平行的直线；
（4）过直线外一点作已知直线的垂线；
A．（1）（2）B．（3）（4）C．（2）（3）D．（1）（4）
5．如果实数a，b满足a+b＝6，ab＝8，那么a2+b2＝( )
A．36B．20C．52D．14
6．如图，把纸片沿折叠，当点落在四边形内部时，则与之间有一种数量关系始终保持不变，试着找一找这个规律你发现的规律是（ ）
A．B．
C．D．
7．若，则下列结论正确的是（ ）
A．B．C．D．
8．如图，中，，点在边上，且，则的度数为（ ）
A．30°B．36°C．45°D．72°
9．下列各数中无理数是（ ）
A．5.3131131113B．C．D．
10．一个两位数的个位数字与十位数字的和为14，若调换个位数字与十位数字，所得的新数比原数小36，则这个两位数是（ ）
A．86B．95C．59D．68
二、填空题(每小题3分,共24分)
11．在弹性限度内，弹簧伸长的长度与所挂物体的质量呈正比，某弹簧不挂物体时长15cm，当所挂物体质量为3kg时，弹簧长1．8cm．写出弹簧长度L（cm）与所挂物体质量x（kg）之间的函数表达式 ．
12．如图，已知点M（-1，0），点N（5m，3m+2）是直线AB：右侧一点，且满足∠OBM=∠ABN，则点N的坐标是_____．
13．甲、乙两人骑自行车匀速同向行驶，乙在甲前面100米处，同时出发去距离甲1300米的目的地，其中甲的速度比乙的速度快.设甲、乙之间的距离为米，乙行驶的时间为秒，与之间的关系如图所示，则甲的速度为每秒___________米.
14．如果ab>1，ac<1．则直线y=x+不经过第___象限．
15．已知，，是的三边，且，则的形状是__________．
16．因式分解：____．
17．已知，且，为两个连续的整数，则___________.
18．已知和的图像交于点，那么关于的二元一次方程组的解是____________．
三、解答题(共66分)
19．（10分）如图，点A、、、在同一直线上，，AF∥DE，.求证：.
20．（6分）如图，，点为上点，射线经过点，且，若，求的度数.
21．（6分）某广告公司为了招聘一名创意策划，准备从专业技能和创新能力两方面进行考核，成绩高者录取．
甲、乙、丙三名应聘者的考核成绩以百分制统计如下表．
（1）如果公司认为专业技能和创新能力同等重要，则应聘人______将被录取．
（2）如果公司认为职员的创新能力比专业技能重要，因此分别赋予它们6和4的权．计算他们赋 权后各自的平均成绩，并说明谁将被录取．
22．（8分）（1）计算：（a﹣b）（a2+ab+b2）
（2）利用所学知识以及（1）所得等式，化简代数式
23．（8分）在等腰△ABC与等腰△ADE中，AB＝AC，AD＝AE，∠BAC＝∠DAE，且点D、E、C三点在同一条直线上，连接BD．
（1）如图1，求证：△ADB≌△AEC
（2）如图2，当∠BAC＝∠DAE＝90°时，试猜想线段AD，BD，CD之间的数量关系，并写出证明过程；
（3）如图3，当∠BAC＝∠DAE＝120°时，请直接写出线段AD，BD，CD之间的数量关系式为： （不写证明过程）
24．（8分）在中，，，点是上的一点，连接，作交于点．

（1）如图1，当时，求证：；
（2）如图2，作于点，当时，求证：；
（3）在（2）的条件下，若，求的值．
25．（10分）某学校为了丰富学生课余生活，开展了“第二课堂”活动，推出了以下四种选修课程：、绘画；、唱歌；、演讲；、书法．学校规定：每个学生都必须报名且只能选择其中的一个课程．学校随机抽查了部分学生，对他们选择的课程情况进行了统计，并绘制了如下两幅不完整的统计图，请结合统计图中的信息解决下列问题：
（1）这次抽查的学生人数是多少人？
（2）将条形统计图补充完整；
（3）在扇形统计图中，求选课程的人数所对的圆心角的度数；
（4）如果该校共有1200名学生，请你估计该校报课程的学生约有多少人？
26．（10分）新春佳节来临，某公司组织10辆汽车装运苹果、芦柑、香梨三种水果共60吨去外地销售，要求10辆汽车全部装满，每辆汽车只能装运同一种水果，且装运每种水果的车辆都不少于2辆，根据下表提供的信息，解答以下问题：
设装运苹果的车辆为x辆，装运芦柑的车辆为y辆，求y与x之间的函数关系式，并直接写出x的取值范围
用w来表示销售获得的利润，那么怎样安排车辆能使此次销售获利最大？并求出w的最大值．
参考答案
一、选择题(每小题3分,共30分)
1、B
2、D
3、C
4、A
5、B
6、A
7、B
8、D
9、C
10、B
二、填空题(每小题3分,共24分)
11、L=2．6x+3．
12、
13、6
14、一
15、等腰三角形
16、
17、2
18、
三、解答题(共66分)
19、详见解析.
20、
21、 (1)甲；(2)乙将被录取，理由见解析.
22、（1）a3﹣b3；（2）m+n
23、（1）见解析；（2）CD＝AD+BD，理由见解析；（3）CD＝AD+BD
24、（1）见解析；（2）见解析；（3）1．
25、（1）这次抽查的学生人数是40人；（2）图见解析；（3）36°；（4）该校报课程的学生约有420人
26、 (1);(2)见解析.
百分制
候选人
专业技能考核成绩
创新能力考核成绩
甲
90
88
乙
80
95
丙
85
90
苹果
芦柑
香梨
每辆汽车载货量吨
7
6
5
每车水果获利元
2500
3000
2000