武汉市第二初级中学2023-2024学年八年级数学第一学期期末教学质量检测模拟试题含答案

这是一份武汉市第二初级中学2023-2024学年八年级数学第一学期期末教学质量检测模拟试题含答案，共7页。试卷主要包含了9的算术平方根是等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
注意事项：
1． 答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。
2．选择题必须使用2B铅笔填涂；非选择题必须使用0．5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。
3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。
4．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题3分,共30分)
1．如图，高速公路上有两点相距10km，为两村庄，已知于，于,现要在上建一个服务站，使得两村庄到站的距离相等，则的长是（ ）km．
A．4B．5C．6D．
2．如果是方程ax＋(a－2)y＝0的一组解，则a的值是( )
A．1B．－1C．2D．－2
3． “某市为处理污水，需要铺设一条长为4000米的管道，为了尽量减少施工对交通所造成的影响，实际施工时×××××．设原计划每天铺设管道x米，则可得方程．”根据此情境，题中用“×××××”表示得缺失的条件，应补为( )
A．每天比原计划多铺设10米，结果延期20天才完成任务
B．每天比原计划少铺设10米，结果延期20天才完成任务
C．每天比原计划多铺设10米，结果提前20天完成任务
D．每天比原计划少铺设10米，结果提前20天完成任务
4．下列银行图标中，是轴对称图形的是( )
A．B．C．D．
5．9的算术平方根是（ ）
A．3B．-3C．D．以上都对
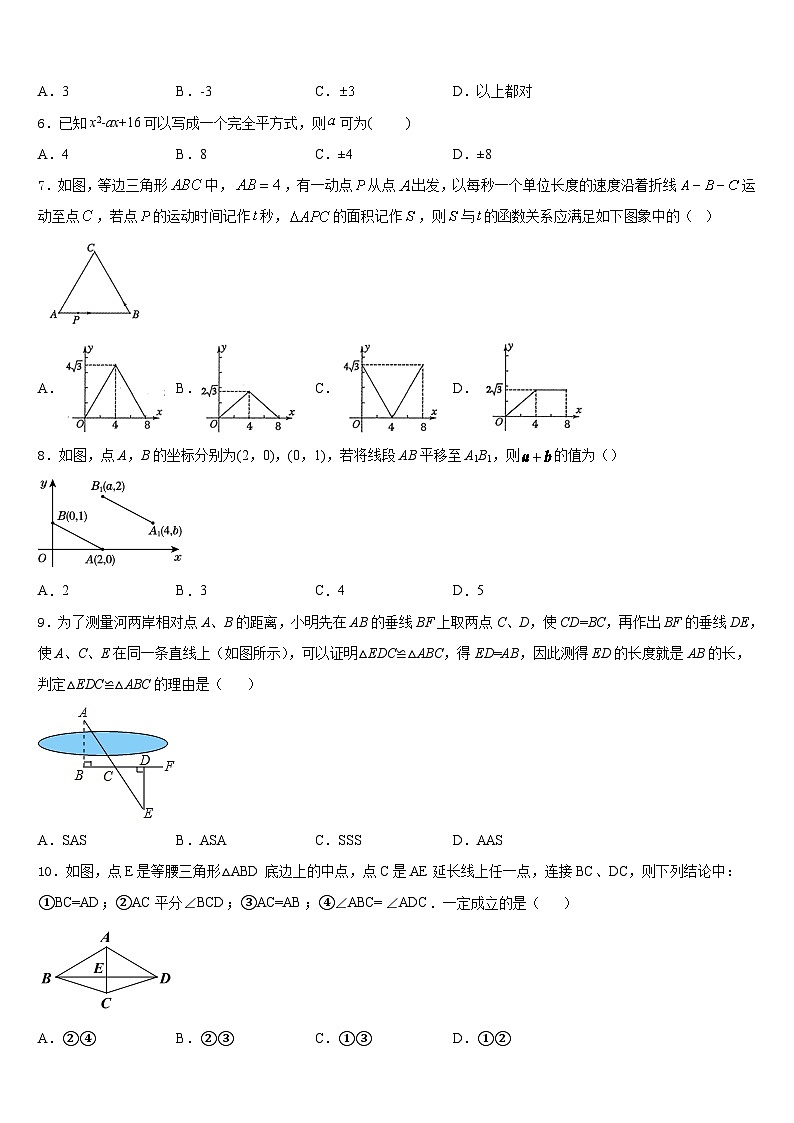
6．已知x2-ax+16可以写成一个完全平方式，则可为( )
A．4B．8C．±4D．±8
7．如图，等边三角形中，，有一动点从点出发，以每秒一个单位长度的速度沿着折线运动至点，若点的运动时间记作秒，的面积记作，则与的函数关系应满足如下图象中的（ ）
A．B．C．D．
8．如图，点A，B的坐标分别为(2，0)，(0，1)，若将线段AB平移至A1B1，则的值为（）
A．2B．3C．4D．5
9．为了测量河两岸相对点A、B的距离，小明先在AB的垂线BF上取两点C、D，使CD=BC，再作出BF的垂线DE，使A、C、E在同一条直线上（如图所示），可以证明△EDC≌△ABC，得ED=AB，因此测得ED的长度就是AB的长，判定△EDC≌△ABC的理由是（ ）
A．SASB．ASAC．SSSD．AAS
10．如图，点E是等腰三角形△ABD底边上的中点，点C是AE延长线上任一点，连接BC、DC，则下列结论中：①BC=AD；②AC平分∠BCD；③AC=AB；④∠ABC=∠ADC．一定成立的是（ ）
A．②④B．②③C．①③D．①②
二、填空题(每小题3分,共24分)
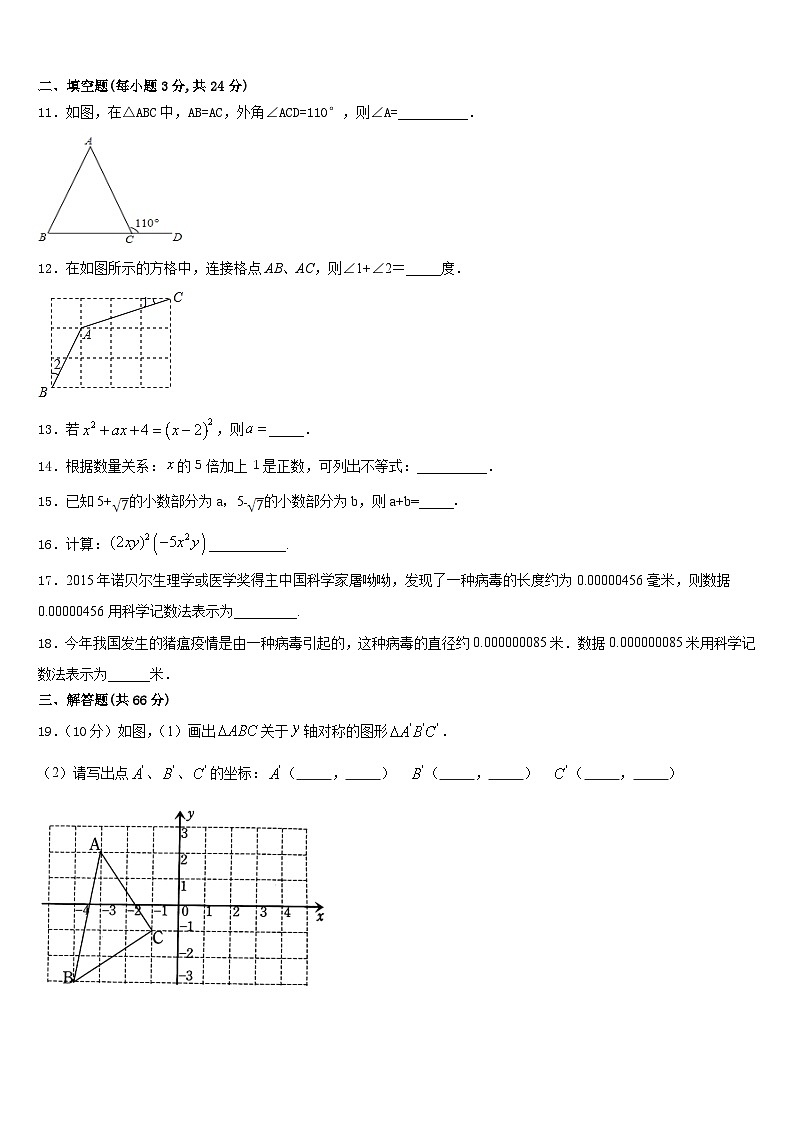
11．如图，在△ABC中，AB=AC，外角∠ACD=110°，则∠A=__________．
12．在如图所示的方格中，连接格点AB、AC，则∠1+∠2＝_____度．
13．若，则_____．
14．根据数量关系：的5倍加上1是正数，可列出不等式：__________．
15．已知5+的小数部分为a，5﹣的小数部分为b，则a+b=_____．
16．计算：___________.
17．2015年诺贝尔生理学或医学奖得主中国科学家屠呦呦，发现了一种病毒的长度约为0.00000456毫米，则数据0.00000456用科学记数法表示为_________.
18．今年我国发生的猪瘟疫情是由一种病毒引起的，这种病毒的直径约0.000000085米．数据0.000000085米用科学记数法表示为______米．
三、解答题(共66分)
19．（10分）如图，（1）画出关于轴对称的图形．
（2）请写出点、、的坐标：（ ， ） （ ， ） （ ， ）
20．（6分）某中学对学生进行“校园安全知识”知识测试，并随机抽取部分学生的成绩进行分析，将成绩分为三个等级：不合格、一般、优秀，并绘制成如下两幅统计图．
请你根据图中所给的信息解答下列问题：
（1）抽取的人数是____________人；补全条形统计图；
（2）“一般”等级所在扇形的圆心角的度数是________度．
21．（6分）如图，在矩形ABCD中，E、F分别是边AB、CD上的点，AE=CF，连接EF、BF，EF与对角线AC交于点O，且BE=BF，∠BEF=2∠BAC．
（1）求证：OE=OF；
（2）若BC=2，求AB的长．
22．（8分）小张和同学相约“五一”节到离家2400米的电影院看电影，到电影院后，发现电影票忘带了，此时离电影开始还有25分钟，于是他跑步回家，拿到票后立刻找到一辆“共享单车”原路赶回电影院，已知小张骑车的时间比跑步的时间少用了4分钟，骑车的平均速度是跑步的平均速度的1.5倍．
（1）求小张跑步的平均速度；
（2）如果小张在家取票和寻找“共享单车”共用了6分钟，他能否在电影开始前赶到电影院？说明理由．
23．（8分）计算：
（1）； （2）
24．（8分）问题情境：如图①,在直角三角形ABC中,∠BAC=90∘,AD⊥BC于点D,可知：∠BAD=∠C(不需要证明)；
(1)特例探究：如图②,∠MAN=90∘,射线AE在这个角的内部,点B.C在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.证明：△ABD≌△CAF；
(2)归纳证明：如图③,点B,C在∠MAN的边AM、AN上,点E,F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角．已知AB=AC,∠1=∠2=∠BAC.求证：△ABE≌△CAF；
(3)拓展应用：如图④，在△ABC中，AB=AC，AB>BC.点D在边BC上，CD=2BD，点E.F在线段AD上，∠1=∠2=∠BAC.若△ABC的面积为18，求△ACF与△BDE的面积之和是多少?
25．（10分）如图，两条公路相交于点O，在交角侧有A、B两个村庄，现在要建一加油站P，使得加油站P到两条公路的距离和到A、B两个村庄的距离相等，请画出加油站P的位置.（用尺规作图，保留作图痕迹，不写作法和证明过程）
26．（10分）因式分解:
（1）；
（2）
参考答案
一、选择题(每小题3分,共30分)
1、A
2、B
3、C
4、D
5、A
6、D
7、A
8、B
9、B
10、A
二、填空题(每小题3分,共24分)
11、40°
12、1
13、-4
14、
15、2
16、－20
17、
18、
三、解答题(共66分)
19、（1）见解析；（2）（3，2）（4，－3）（1，－1）
20、（1）120，图详见解析；（2）108
21、（1）证明见解析；（2）1.
22、（1）小张跑步的平均速度为1米/分；（2）小张不能在电影开始前赶到电影院.
23、（1）；（2）
24、（1）见解析；（2）见解析；（3）6.
25、详见解析.
26、（1）；（2）.