2023-2024学年郑州二中学八年级数学第一学期期末质量跟踪监视模拟试题含答案

这是一份2023-2024学年郑州二中学八年级数学第一学期期末质量跟踪监视模拟试题含答案，共8页。试卷主要包含了考生必须保证答题卡的整洁，下列图形中，具有稳定性的是，如图，已知直线AB，下列各式计算正确的是，2 的平方根是等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
考生请注意：
1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。
2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。
3．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1．若（x﹣2）（x+3）＝x2+ax+b，则a，b的值分别为（ ）
A．a＝5，b＝﹣6B．a＝5，b＝6C．a＝1，b＝6D．a＝1，b＝﹣6
2．已知点A（2﹣a，3）与点B（1，b﹣1）关于x轴对称，则（a+b）2019的值为（ ）
A．0B．1C．﹣1D．32019
3．下列四个数中，是无理数的是（ ）
A．B．C．D．
4．下列图形中，具有稳定性的是（ ）
A．正方形B．长方形C．三角形D．平行四边形
5．如图，已知直线AB：y=x+分别交x轴、y轴于点B、A两点,C（3，0），D、E分别为线段AO和线段AC上一动点，BE交y轴于点H,且AD＝CE，当BD＋BE的值最小时，则H点的坐标为（ ）
A．（0，4）B．（0，5）C．（0，）D．（0，）
6．如图，DE是△ABC中边AC的垂直平分线，若BC＝18cm，AB＝10cm，则△ABD的周长为（ ）
A．16cmB．28cmC．26cmD．18cm
7．一项工程，一半由甲单独做需要m小时完成，另一半由乙单独做需要n小时完成，则甲、乙合做这项工程所需的时间为（ ）
A．小时B．小时C．小时D．小时
8．下列各式计算正确的是（ ）．
A．a2•a3=a6B．（﹣a3）2=a6C．（2ab）4=8a4b4D．2a2﹣3a2=1
9．能说明命题“对于任何实数a, 都有>-a”是假命题的反例是（）
A．a=-2B．aC．a=1D．a=2
10．2 的平方根是 （ ）
A．2B．-2C．D．
二、填空题(每小题3分,共24分)
11．将一张长方形纸片按如图5所示的方式折叠,BC、BD为折痕,则∠CBD为___度.
12．如图，在中，，，，则的长是_______．
13．已知，则的值等于___________．
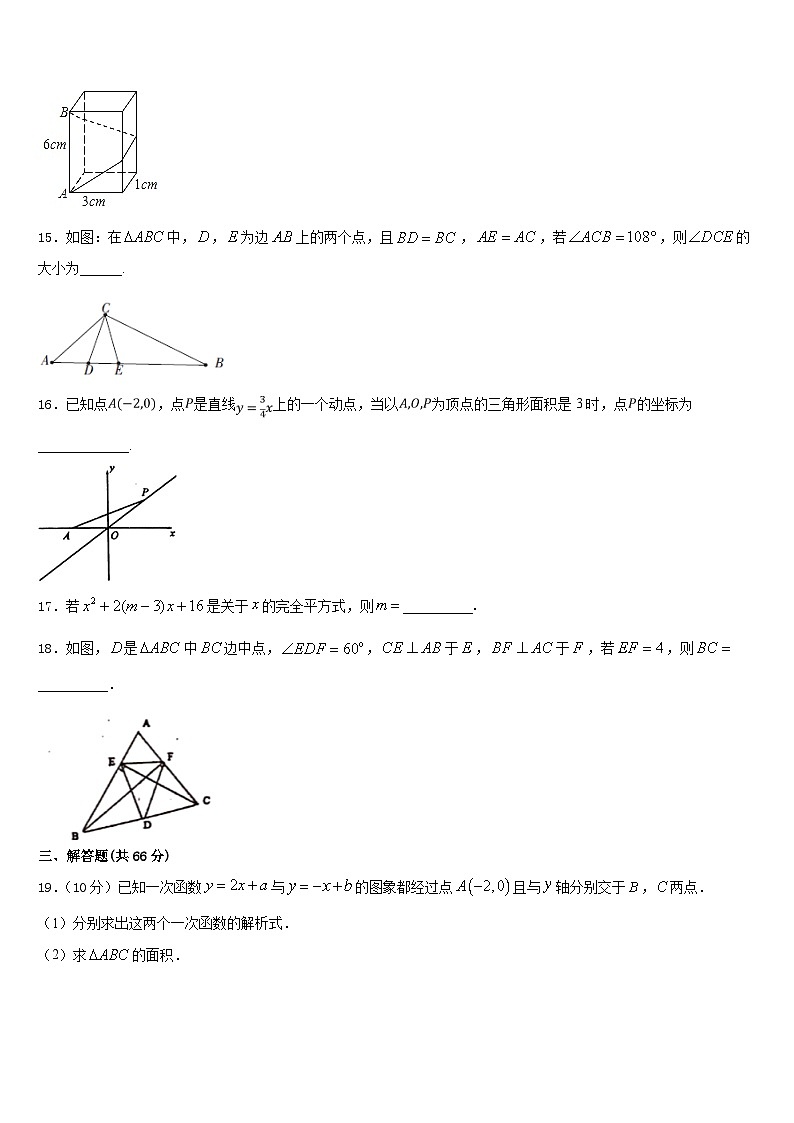
14．如图，长方体的底面边长分别为1cm 和3cm，高为6cm．如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B，那么所用细线最短需要_____cm．
15．如图：在中，，为边上的两个点，且，，若，则的大小为______.
16．已知点，点是直线上的一个动点，当以为顶点的三角形面积是3时，点的坐标为_____________.
17．若是关于的完全平方式，则__________．
18．如图，是中边中点，，于，于，若，则__________．
三、解答题(共66分)
19．（10分）已知一次函数与的图象都经过点且与轴分别交于，两点．
（1）分别求出这两个一次函数的解析式．
（2）求的面积．
20．（6分）A、B两种机器人都被用来搬运化工原料，A型机器人比B型机器人每小时多搬运30kg，A型机器人搬运900kg与B型机器人搬运600kg所用时间相等，两种机器人每小时分别搬运多少化工原料？
21．（6分）如图,为正方形的边的延长线上一动点，以为一边做正方形，以为一顶点作正方形,且在的延长线上（提示：正方形四条边相等，且四个内角为）
（1）若正方形、的面积分别为，，则正方形的面积为 （直接写结果）.
（2）过点做的垂线交的平分线于点,连接,试探求在点运动过程中，的大小是否发生变化，并说明理由.
22．（8分）如图，已知AC平分∠BAD，CE⊥AB于E，CF⊥AD于F，且BC＝CD．
（1）求证：△BCE≌△DCF；
（2）若AB＝21，AD＝9，BC＝CD＝10，求AC的长．
23．（8分）某区在实施居民用水额定管理前，对居民生活用水情况进行了调查，下表是通过简单随机抽样获得的50个家庭去年月平均用水量（单位：吨），并将调查数据进行如下整理：
4.7 2.1 3.1 2.3 5.2 2.8 7.3 4.3 4.8 6.7
4.5 5.1 6.5 8.9 2.2 4.5 3.2 3.2 4.5 3.5
3.5 3.5 3.6 4.9 3.7 3.8 5.6 5.5 5.9 6.2
5.7 3.9 4.0 4.0 7.0 3.7 9.5 4.2 6.4 3.5
4.5 4.5 4.6 5.4 5.6 6.6 5.8 4.5 6.2 7.5
频数分布表
（1）把上面频数分布表和频数分布直方图补充完整；
（2）从直方图中你能得到什么信息？（写出两条即可）；
（3）为了鼓励节约用水，要确定一个用水量的标准，超出这个标准的部分按1.5倍价格收费，若要使60%的家庭收费不受影响，你觉得家庭月均用水量应该定为多少？为什么？
24．（8分）如图1，在Rt△ABC中，∠C＝90°，AC＝BC，点D，E分别在边AC，BC上，CD＝CE，连接AE，点F，H，G分别为DE，AE，AB的中点连接FH，HG
（1）观察猜想图1中，线段FH与GH的数量关系是 ，位置关系是
（2）探究证明：把△CDE绕点C顺时针方向旋转到图2的位置，连接AD，AE，BE判断△FHG的形状，并说明理由
（3）拓展延伸：把△CDE绕点C在平面内自由旋转，若CD＝4，AC＝8，请直接写出△FHG面积的最大值
25．（10分）如图1，在边长为3的等边中，点从点出发沿射线方向运动，速度为1个单位/秒，同时点从点出发，以相同的速度沿射线方向运动，过点作交射线于点，连接交射线于点．
（1）如图1，当时，求运动了多长时间？
（2）如图1，当点在线段（不考虑端点）上运动时，是否始终有？请说明理由；
（3）如图2，过点作，垂足为，当点在线段（不考虑端点）上时，的长始终等于的一半；如图3，当点运动到的延长线上时，的长是否发生变化？若改变，请说明理由；若不变，求出的长．
26．（10分）老师在黑板上书写了一个代数式的正确计算结果，随后用手遮住了原代数式的一部分，如图：
（1）求被手遮住部分的代数式，并将其化简；
（2）原代数式的值能等于-1吗？请说明理由.
参考答案
一、选择题(每小题3分,共30分)
1、D
2、C
3、A
4、C
5、A
6、B
7、D
8、B
9、A
10、D
二、填空题(每小题3分,共24分)
11、90
12、
13、
14、1
15、
16、（4，3）或（-4，-3）
17、1或-1
18、1
三、解答题(共66分)
19、（1）和；（2）
20、A型机器人每小时搬运kg化工原料，B型机器人每小时搬运kg化工原料.
21、（1）；（2）的大小不会发生变化，理由见解析.
22、（1）见解析；（2）AC的长为1．
23、详见解析
24、（1）FH＝GH，FH⊥HG；（2）△FGP是等腰直角三角形，理由见解析；（3）2
25、（1）运动了1秒；（2）始终有，证明见解析；（3）不变，．
26、（1）；（2）原代数式的值不能等于-1，理由见详解
分组
划记
频数
2.0＜x≤3.5
正正
11
3.5＜x≤5.0
19
5.0＜x≤6.5
6.5＜x≤8.0
8.0＜x≤9.5
2
合计
50