2023-2024学年浙江省绍兴市柯桥区实验中学数学八年级第一学期期末质量跟踪监视试题含答案

这是一份2023-2024学年浙江省绍兴市柯桥区实验中学数学八年级第一学期期末质量跟踪监视试题含答案，共8页。试卷主要包含了答题时请按要求用笔，已知，则M等于，下列计算正确的是等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
注意事项:
1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。
2．答题时请按要求用笔。
3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。
4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。
5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题3分,共30分)
1．如图，△ABC的外角∠ACD的平分线CP与∠ABC平分线BP交于点P，若∠BPC=40°，则∠CAP的度数是（ ）
A．30°；B．40°；C．50°；D．60°.
2．下列图案属于轴对称图形的是( )
A．B．C．D．
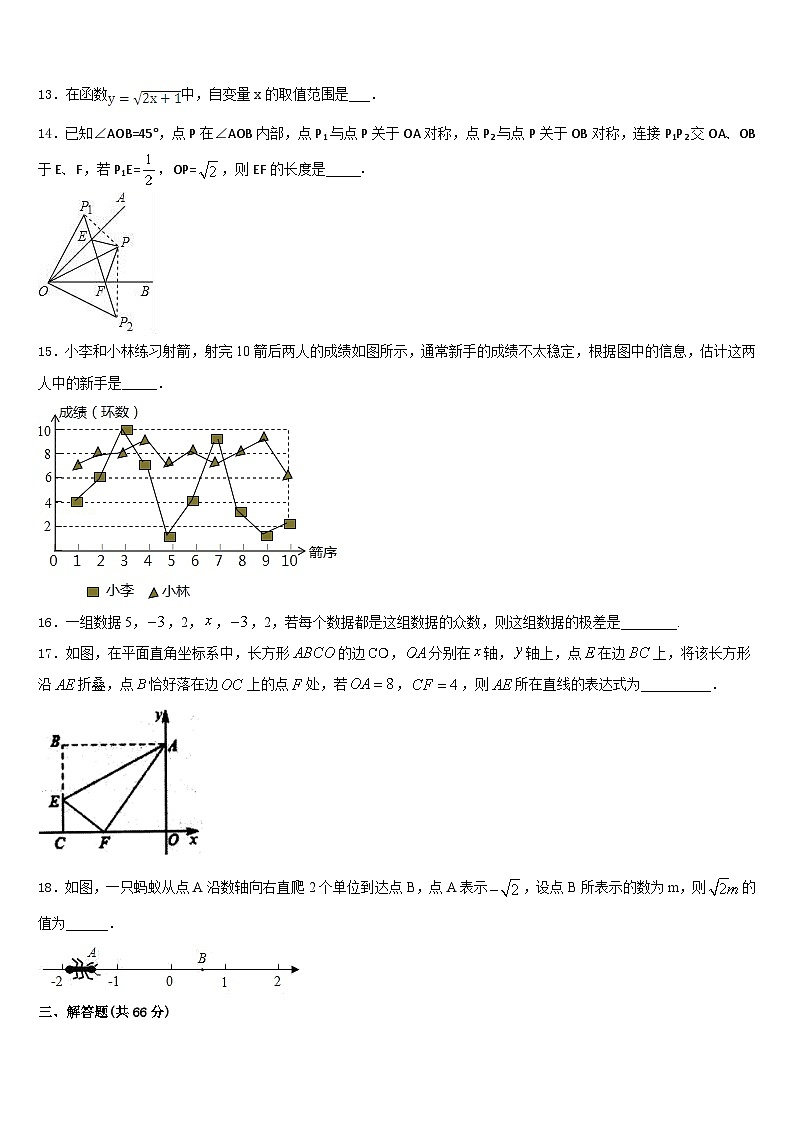
3．科学家可以使用冷冻显微术以高分辨率测定溶液中的生物分子结构，使用此技术测定细菌蛋白结构的分辨率达到0.22纳米，也就是0.000 000 000 22米．将0.000 000 000 22用科学记数法表示为（ ）
A．0.22×10﹣9B．2.2×10﹣10C．22×10﹣11D．0.22×10﹣8
4．如图，已知，，则（ ）
A．75°B．70°C．65°D．60°
5．如图，在△中，，将△绕点顺时针旋转，得到△，连接，若，，则线段的长为（ ）
A．B．C．D．
6．若（x+a）（x﹣2）＝x2+bx﹣6，则a、b的值是（ ）
A．a＝3，b＝5B．a＝3，b＝1C．a＝﹣3，b＝﹣1D．a＝﹣3，b＝﹣5
7．已知，则M等于（ ）
A．B．C．D．
8．若（x+m）（x﹣8）中不含x的一次项，则m的值为（ ）
A．8B．﹣8C．0D．8或﹣8
9．下列计算正确的是（ ）
A．a3·a4 = a12B．(a3)2 = a5
C．(－3a2)3 =－9a6D．(－a2)3 =－a6
10．如图，已知△ABC中，∠ABC＝45°，AC＝4，H是高AD和BE的交点，则线段BH的长度为（ ）
A．6B．5C．4D．3
二、填空题(每小题3分,共24分)
11．如图，在与中，，，，若，则的度数为________．
12．已知点P(a+3，2a+4)在x轴上，则点P的坐标为________．
13．在函数中，自变量x的取值范围是___．
14．已知∠AOB=45°，点P在∠AOB内部，点P1与点P关于OA对称，点P2与点P关于OB对称，连接P1P2交OA、OB于E、F，若P1E=，OP=，则EF的长度是_____．
15．小李和小林练习射箭，射完10箭后两人的成绩如图所示，通常新手的成绩不太稳定，根据图中的信息，估计这两人中的新手是_____．
16．一组数据5，，2，，，2，若每个数据都是这组数据的众数，则这组数据的极差是________.
17．如图，在平面直角坐标系中，长方形的边，分别在轴，轴上，点在边上，将该长方形沿折叠，点恰好落在边上的点处，若，，则所在直线的表达式为__________．
18．如图，一只蚂蚁从点A沿数轴向右直爬2个单位到达点B，点A表示，设点B所表示的数为m，则的值为______．
三、解答题(共66分)
19．（10分）如图，是边长为的等边三角形若点以的速度从点向点运动，到点停止运动；同时点以的速度从点向点运动，到点停止运动，
(1)试求出运动到多少秒时，为等边三角形；
(2)试求出运动到多少秒时，为直角三角形．
20．（6分）解方程组：.
21．（6分）为做好食堂的服务工作，某学校食堂对学生最喜爱的菜肴进行了抽样调查，下面试根据收集的数据绘制的统计图（不完整）：
（1）参加抽样调查的学生数是______人，扇形统计图中“大排”部分的圆心角是______°；
（2）把条形统计图补充完整；
（3）若全校有3000名学生，请你根据以上数据估计最喜爱“烤肠”的学生人数．

22．（8分）数学课上,李老师出示了如下的题目：如图1，在等边中，点在上，点在的延长线上，且，试确定线段与的大小关系，并说明理由，
（1）小敏与同桌小聪探究解答的思路如下：
①特殊情况，探索结论，
当点为的中点时，如图2，确定线段与的大小关系，请你直接写出结论：______．(填>，<或=)
②特例启发，解答题目，
解：题目中，与的大小关系是：______．(填>，<或=)
理由如下：如图3，过点作，交于点，(请你补充完成解答过程)
（2）拓展结论，设计新题，
同学小敏解答后，提出了新的问题：在等边中，点在直线上，点在直线上，且，已知的边长为，求的长?(请直接写出结果)
23．（8分）一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，慢车的速度是快车速度的，两车同时出发．设慢车行驶的时间为x（h），两车之间的距离为y（km），图中的折线表示y与x之间的函数关系．
根据图象解决以下问题：
（1）甲、乙两地之间的距离为 km；D点的坐标为 ；
（2）求线段BC的函数关系式，并写出自变量x的取值范围；
（3）若第二列快车从乙地出发驶往甲地，速度与第一列快车相同．在第一列快车与慢车相遇30分钟后，第二列快车追上慢车．求第二列快车比第一列快车晚出发多少小时？
24．（8分）先化简，再求值，其中．
25．（10分）中国海军亚丁湾护航十年，中国海军被亚丁湾上来往的各国商船誉为“值得信赖的保护伞”．如图，在一次护航行动中，我国海军监测到一批可疑快艇正快速向护航的船队靠近，为保证船队安全，我国海军迅速派出甲、乙两架直升机分别从相距40海里的船队首（点）尾（点）前去拦截，8分钟后同时到达点将可疑快艇驱离．己知甲直升机每小时飞行180海里，航向为北偏东，乙直升机的航向为北偏西，求乙直升机的飞行速度（单位：海里/小时）．
26．（10分）如图，已知AB=CD，AE⊥BD，CF⊥BD，垂足分别为E、F，BF=DE．
求证：（1）BE=DF；
（2）△DCF≌△BAE；
（3）分别连接AD、BC，求证AD∥BC．
参考答案
一、选择题(每小题3分,共30分)
1、C
2、A
3、B
4、B
5、A
6、B
7、A
8、A
9、D
10、C
二、填空题(每小题3分,共24分)
11、40°
12、 (1，0)
13、
14、
15、小李．
16、1
17、
18、
三、解答题(共66分)
19、（1）秒；（2）秒或1.5秒
20、
21、（1）200，144；（2）答案见解析；（3）600
22、（1）①AE=DB；②=；理由见解析；（2）2或1．
23、（1）1200，D（11，1200）；（2）y=240x-1200（1≤x≤7.1）；（3）2.71小时．
24、；
25、乙直升机的飞行速度为每小时飞行240海里．
26、（1）证明见解析；（2）证明见解析；（3）证明见解析.