河南省南阳市新野县2022-2023学年七年级上学期期末数学试题+

这是一份河南省南阳市新野县2022-2023学年七年级上学期期末数学试题+，共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.当−a=−7时，−a的相反数是( )
A. 7B. −7C. ±7D. 不能确定
2.下列计算正确的是( )
A. 13−13×4=0×4=0
B. 5÷(−2)×(−12)=5÷1=5
C. (36−12)÷32=36×23−12×23=16
D. 24−(4×32)=24−4×6=0
3.已知一个多项式与2x2−4的差是x2−2x，则这个多项式是( )
A. x2+2x−4B. 3x2−6xC. −x2−2x−4D. 3x2−2x−4
4.下列计算正确的是( )
A. 7ab−(−3ab)=4abB. 2(a+2b)=2a+2b
C. −ab2+2a2b=a2bD. 3m2−4m2=−m2
5.如图，裁掉一个正方形后能折叠成正方体，但不能裁掉的是( )
A. ①
B. ②
C. ③
D. ④
6.如图是某几何体的三视图，则这个几何体是( )
A. B. C. D.
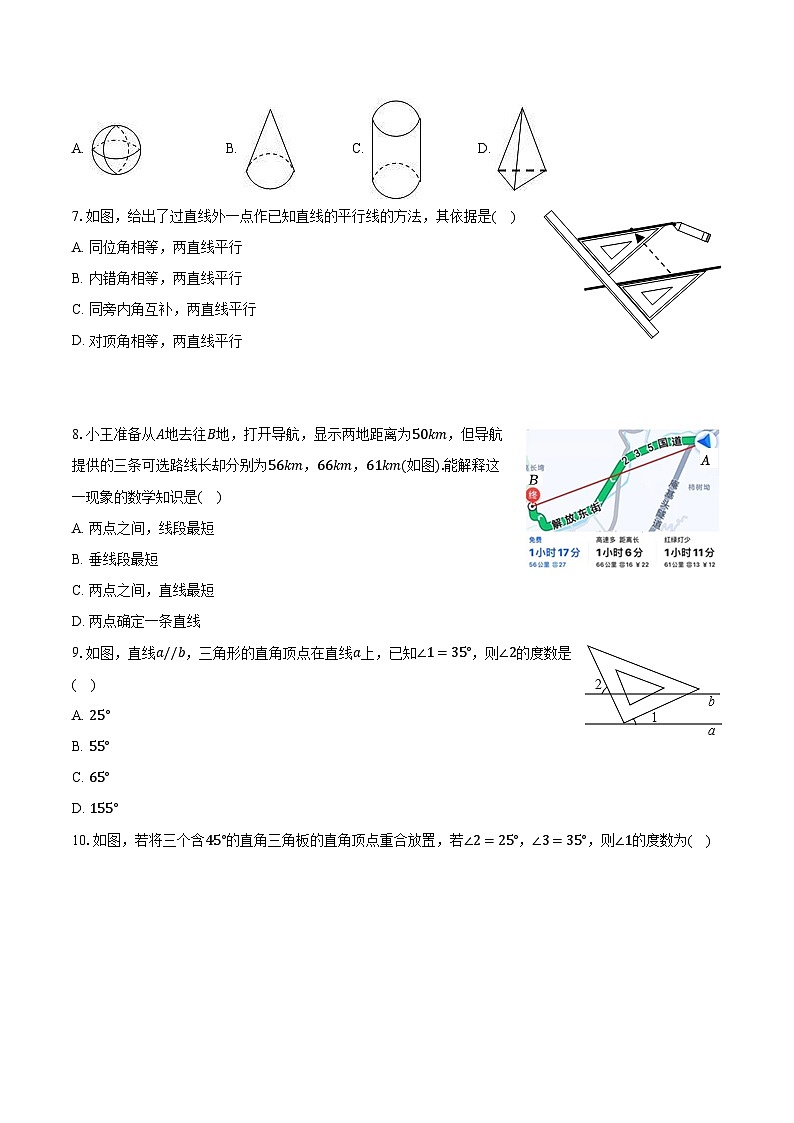
7.如图，给出了过直线外一点作已知直线的平行线的方法，其依据是( )
A. 同位角相等，两直线平行
B. 内错角相等，两直线平行
C. 同旁内角互补，两直线平行
D. 对顶角相等，两直线平行
8.小王准备从A地去往B地，打开导航，显示两地距离为50km，但导航提供的三条可选路线长却分别为56km，66km，61km(如图).能解释这一现象的数学知识是( )
A. 两点之间，线段最短
B. 垂线段最短
C. 两点之间，直线最短
D. 两点确定一条直线
9.如图，直线a/​/b，三角形的直角顶点在直线a上，已知∠1=35°，则∠2的度数是( )
A. 25°
B. 55°
C. 65°
D. 155°
10.如图，若将三个含45°的直角三角板的直角顶点重合放置，若∠2=25°，∠3=35°，则∠1的度数为( )
A. 25°B. 30°C. 35°D. 40°
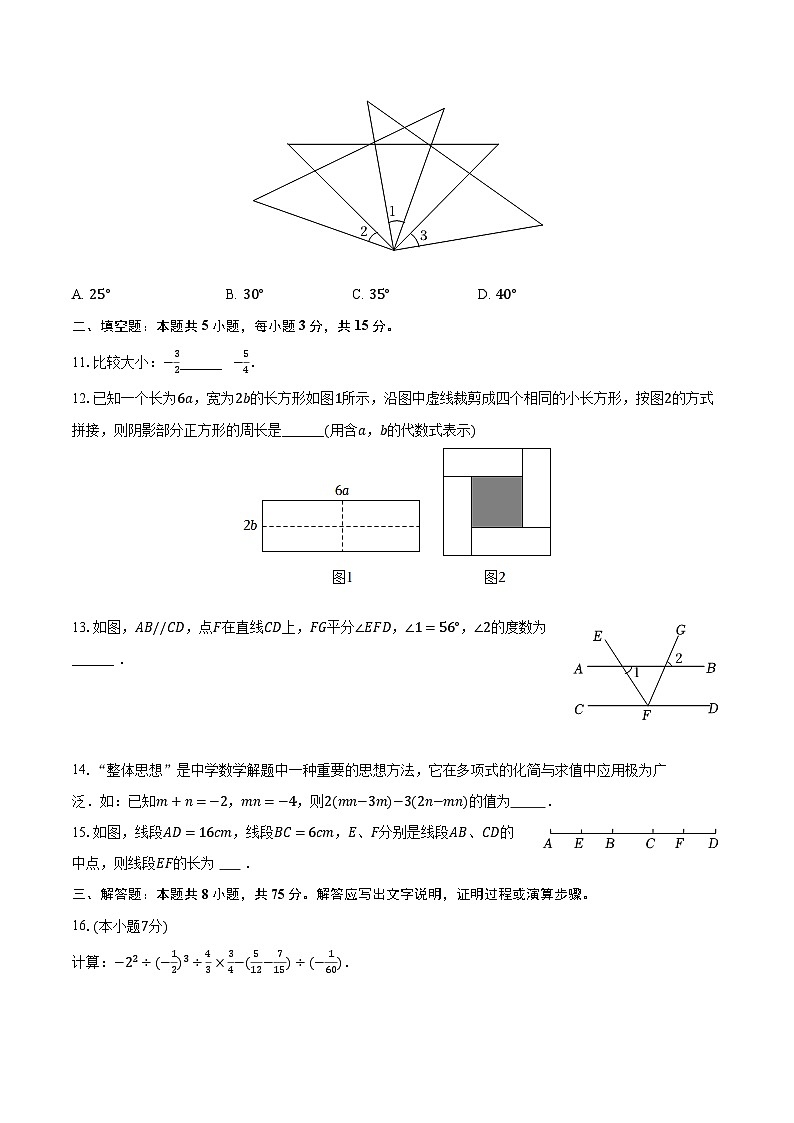
二、填空题：本题共5小题，每小题3分，共15分。
11.比较大小：−32______ −54．
12.已知一个长为6a，宽为2b的长方形如图1所示，沿图中虚线裁剪成四个相同的小长方形，按图2的方式拼接，则阴影部分正方形的周长是______(用含a，b的代数式表示)
13.如图，AB/​/CD，点F在直线CD上，FG平分∠EFD，∠1=56°，∠2的度数为______ ．
14.“整体思想”是中学数学解题中一种重要的思想方法，它在多项式的化简与求值中应用极为广泛．如：已知m+n=−2，mn=−4，则2(mn−3m)−3(2n−mn)的值为 ．
15.如图，线段AD=16cm，线段BC=6cm，E、F分别是线段AB、CD的中点，则线段EF的长为 ．
三、解答题：本题共8小题，共75分。解答应写出文字说明，证明过程或演算步骤。
16.(本小题7分)
计算：−22÷(−12)3÷43×34−(512−715)÷(−160)．
17.(本小题14分)
(1)化简求值：4xy2−[2x2y−3(−43xy2+12x2y)+xy2]，其中x，y满足|x+2|+(y−1)2=0；
(2)已知多项式(x2+ax−y+b)与(bx2−3x+6y−3)差的值与字母x无关，求代数式3(a2−2ab−b2)−a的值．
18.(本小题6分)
按要求画图：(保留作图痕迹)
已知：线段a、b、c
画法：
(1)画线段AB使AB=a，延长AB到C，使线段BC=b．
(2)用三角板过点A画AB的垂线AP，并画上直角符号．
(3)用圆规在射线AP上截取AD=c．
(4)连接CD．
19.(本小题9分)
如图是由若干个边长为1的立方块搭成的几何体从上面看到的平面图形，小正方形中的数字表示该位置立方块的个数．
(1)请画出该几何体从正面和从左面看到的平面图形；
(2)求该几何体的表面积．
20.(本小题9分)
为了迎接镇中心学校第五届艺术节的召开，现要从七、八年级学生中抽调a人参加“校园集体舞”、“广播体操”、“唱红歌”等训练活动，其中参加“校园集体舞”人数是抽调人数的14还多3人，参加“广播体操”活动人数是抽调人数的12少2人，其余的参加“唱红歌”活动，若抽调的每个学生只参加了一项活动．
(1)求参加“唱红歌”活动的人数．(用含a的式子表示)
(2)求参加“广播体操”比参加“校园集体舞蹈”多的人数．(用含a的式子表示)
(3)求当a=84时，参加“广播体操比赛”的人数．
21.(本小题9分)
如图，已知直线a，b与直线c，d相交，∠1=∠2，∠3=110°，求∠4的度数．
22.(本小题10分)
已知O是AB上的一点，∠COD是直角，OE平分∠BOC．
(1)如图①，若∠AOC=30°，求∠DOE的度数；
(2)将图①中的∠COD绕顶点O顺时针旋转至图②的位置，猜想∠AOC与∠DOE之间存在什么样的数量关系，写出你的结论，并说明理由．
23.(本小题11分)
问题情境：如图①，直线AB/​/CD，点E，F分别在直线AB，CD上．
猜想：(1)若∠1=130°，∠2=150°，试猜想∠P= °；
探究：(2)在图①中探究∠1，∠2，∠P之间的数量关系，并证明你的结论；
拓展：(3)将图①变为图②，若∠1+∠2=325°，∠EPG=75°，求∠PGF的度数．
答案和解析
1.【答案】A
【解析】解：当−a=−7时，−7的相反数是7．
−a的相反数是7．
故选：A．
根据相反数的定义解答即可．
本题考查了相反数，掌握相反数的定义是解答本题的关键．相反数的定义：只有符号不同的两个数叫做互为相反数．
2.【答案】C
【解析】解：A.原式=13−43=−1，选项错误，不符合题意；
B.原式=+5×12×12=54，选项错误，不符合题意；
C.原式=24×23=16，选项正确，符合题意；
D.原式=24−4×9=24−36=−12，选项错误，不符合题意；
故选：C．
根据先计算有理数乘法与再计算减法判断A；根据有理乘除混合运算法则判断B；根据有理数除法法则与乘法分配律判断C；根据有理数混合运算顺序，运算法则判断D．
本题主要考查了有理数的混合运算，熟记有理数的运算顺序，运算法则，运算定律是解题的关键．
3.【答案】D
【解析】解：因为，一个多项式与2x2−4的差是x2−2x，
所以，这个多项式=(2x2−4)+(x2−2x)
=2x2−4+x2−2x
=3x2−2x−4，
故选：D．
根据题意列出算式，再去括号、合并同类项即可．
本题主要考查整式加减，解题的关键是掌握去括号、合并同类项法则．
4.【答案】D
【解析】解：A、7ab−(−3ab)=10ab，不符合题意；
B、2(a+2b)=2a+4b，不符合题意；
C、不是同类项，不能合并，不符合题意；
D、3m2−4m2=−m2，符合题意．
故选：D．
根据合并同类项法则和去括号法则计算即可求解．
本题考查了整式的加减，整式的加减的实质就是去括号、合并同类项．一般步骤是：先去括号，然后合并同类项．
5.【答案】A
【解析】解：如图，裁掉一个正方形后能折叠成正方体，但不能裁掉的是①，
故选：A．
根据正方体的表面展开图，即可解答．
本题考查了展开图折叠成几何体，熟练掌握正方体的表面展开图是解题的关键．
6.【答案】B
【解析】解：由俯视图易得几何体的底面为圆，还有表示锥顶的圆心，符合题意的只有圆锥．故选B．
主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形．
本题考查由三视图确定几何体的形状，主要考查学生空间想象能力以及对立体图形的认识．
7.【答案】A
【解析】解：如图，给出了过直线外一点作已知直线的平行线的方法，其依据是同位角相等，两直线平行．
故选：A．
根据两角的位置，结合平行线的判定方法，即可得出结论．
本题考查了平行线的判定方法，关键是分析图形，看看相等的是同位角、内错角，还是互补的同旁内角．
8.【答案】A
【解析】解：从A地去往B地，打开导航、显示两地距离为50km，理由是两点之间线段最短，
故选：A．
根据线段的性质，可得答案．
本题考查了线段的性质，熟记线段的性质并应用是解题的关键．
9.【答案】B
【解析】解：如图，∵a/​/b，
∴∠2=∠3，
又∵∠1+∠3=90°，且∠1=35°，
∴∠3=90°−35°=55°，
∴∠2=55°，
故选B．
根据平行线的性质可得∠1+∠2=90°，可求得∠2．
本题主要考查平行线的性质，掌握两直线平行同位角相等是解题的关键．
10.【答案】B
【解析】解：
∵∠AOB=∠COD=90°
∴∠4=∠AOC=25°，
∴∠1=∠EOF−∠2−∠DOF=90°−25°−35°=30°，
故选：B．
求出∠4即可解决问题．
本题考查等腰直角三角形的性质，角的和差定义等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．
11.【答案】<
【解析】【分析】
本题考查了有理数的大小比较，属于基础题，掌握有理数的大小比较法则是关键．根据两个负数，绝对值大的其值反而小，进行比较即可．
【解答】
解：∵|−32|>|−54|，
∴−32<−54．
故答案为：<．
12.【答案】12a−4b
【解析】解：由图可得，
图2中每个小长方形的长为3a，宽为b，
则阴影部分正方形的边长是3a−b，阴影部分正方形的周长是(3a−b)×4=12a−4b．
故答案为：12a−4b．
根据题意和题目中的图形，可以得到图2中小长方形的长和宽，从而可以得到阴影部分正方形的边长，进一步得到阴影部分正方形的周长．
本题考查列代数式，解答本题的关键是明确题意，得到小长方形的长和宽，利用数形结合的思想解答．
13.【答案】62°
【解析】解：因为AB/​/CD，
所以∠1=∠EFC=56°，∠2=∠GFD，
因为GF平分∠EFD，
所以∠GFD=(180°−56°)÷2=62°，
所以∠2=62°．
故答案为：62°．
根据平行线的性质得到∠1=∠EFC=56°，∠2=∠GFD，再根据角平分线的性质求出度数．
此题主要考查平行线的性质，角平分线的性质，熟记平行线的性质是解题的关键．
14.【答案】−8
【解析】【分析】
此题考查了整式的加减−化简求值，熟练掌握运算法则是解本题的关键.原式去括号合并同类项后，将已知等式代入计算即可求出值．
【解答】
解：∵m+n=−2，mn=−4，
∴原式=2mn−6m−6n+3mn，
=5mn−6(m+n)，
=−20+12，
=−8．
故答案为−8．
15.【答案】11cm
【解析】解：∵AD=16cm，BC=6(cm)，
∴AB+CD=16−6=10(cm)，
∵点E、F分别是线段AB、CD的中点
∴EB+CF=AE+DF=12(AB+CD)=5cm，
∴EF=BE+BC+CF=5+6=11(cm)．
故答案为：11cm．
根据题意、结合图形求出AB+CD的长，根据线段中点的性质求出EB+CF，进一步可求出EF．
本题考查的是两点间的距离的计算，掌握线段中点的概念和性质、灵活运用数形结合思想是解题的关键．
16.【答案】解：−22÷(−12)3÷43×34−(512−715)÷(−160)
=−4÷(−18)×34×34−(512−715)×(−60)
=−4×(−8)×34×34+25−28
=18+25−28
=15．
【解析】先算乘方，再算乘除法，然后算加减法即可．
本题考查有理数的混合运算，熟练掌握运算法则是解答本题的关键，注意乘法分配律的应用．
17.【答案】解：(1)∵|x+2|+(y−1)2=0，
∴x+2=0，y−1=0，
∴x=−2，y=1，
原式=4xy2−2x2y−4xy2+32x2y−xy2
=−xy2−12x2y，
当x=−2，y=1时，
原式=−(−2)×1−12×(−2)2×1=2−2=0；
(2)x2+ax−y+b−(bx2−3x+6y−3)
=x2+ax−y+b−bx2+3x−6y+3
=(1−b)x2+(a+3)x−7y+b+3，
∵多项式x2+ax−y+b与bx2−3x+6y−3差的值与字母x的取值无关，
∴1−b=0，a+3=0，
∴b=1，a=−3，
3(a2−2ab−b2)−a=3a2−6ab−3b2−a，
当b=1，a=−3时．
原式=3×(−3)2−6×(−3)×1−3×12+3
=27+18−3+3
=45．
【解析】(1)先根据绝对值和平方的非负性，以及|x+2|+(y−1)2=0，求得x，y的值，再把已知的整式化简，最后代入求值；
(2)先根据代数式的差与字母x无关，求出a、b的值，再化简代数式，代入计算．
本题考查了整式的化简求值，掌握去括号法则、合并同类项法则及绝对值的意义是解决本题的关键．
18.【答案】【详解】(1)解：如图所示，AB=a，BC=b

(2)解：如图所示AP⊥AB，

(3)解：如图3，AD=c

(4)解：连接CD，如图所示
．
【解析】(1)用尺规按画一条线段等于已知的要求作图即可；
(2)按要求画即可；
(3)按要求画即可；
(4)按要求画即可．
本题考查了作图−基本作图，画一条线段等于已知线段，过一点画线段的垂线等知识，熟悉作图的步骤是关键．
19.【答案】解：(1)如图所示：
；
(2)几何体的表面积为2×(5+5+3)=26．
【解析】(1)利用从上面看的图形即可得出几何体的形状，进而分别得出从正面看、从左面看到的平面图形；
(2)利用几何体的形状得出其表面积．
此题主要考查了从不同方向观察物体的形状以及几何体的表面积，正确想象出几何体的形状是解题关键．
20.【答案】解：(1)由题意得，参加“唱红歌”活动的人数为a−(14a+3)−(12a−2)=14a−1(人)，
答：参加“唱红歌”活动的人数为(14a−1)人；
(2)12a−2−(14a+3)=14a−5(人)，
答：参加“广播体操”比参加“校园集体舞蹈”多(14a−5)人；
(3)12a−2=12×84−2=40(人)，
答：当a=84时，参加“广播体操比赛”的人数为40人．
【解析】本题主要考查了列代数式和代数式求值，根据题意找出各量间的和差倍分关系是解答此题的关键．
(1)根据题意参加活动的人数减去校园集体舞人数再减去广播体操人数是唱红歌的人数；
(2)参加“广播体操”的人数减去参加“校园集体舞蹈”的人数即可；
(3)把a=84代入12a−2即可．
21.【答案】解：如图，
∵∠1=∠2，
∴a/​/b，
∴∠5=∠3=110°，
∴∠4=180°−110°=70°，
．
【解析】根据“同位角相等，两直线平行”这一定理，可知a/​/b，再根据“两直线平行，同位角相等”即可解答．
本题主要考查了平行线的判定和性质，平行线的判定是由角的数量关系判断两直线的位置关系，平行线的性质是由平行关系来寻找角的数量关系．
22.【答案】解：(1)∵∠AOC=30°，
∴∠BOC=180°−∠AOC=150°，
∵OE平分∠BOC，
∴∠COE=∠BOE=75°，
∵∠COD=90°，
∴∠DOE=90°−75°=15°；
(2)∠AOC=2∠DOE．
理由是：∵∠COD=90°，∠BOE=∠COE，
∴∠DOE=90°−∠COE，
∴2∠DOE=180°−2∠COE=180°−∠BOC，
∵∠AOC=180°−∠BOC，
∴∠AOC=2∠DOE．
【解析】(1)求出∠BOC，根据角平分线定义求出∠COE，即可求出答案；
(2)求出∠AOC=180°−∠BOC，∠DOE=90°−∠COE，即可得出答案．
本题考查了角平分线定义和对顶角、邻补角等知识点，能灵活运用邻补角互补进行计算是解此题的关键．
23.【答案】解：(1)80；
(2)∠EPF=360°−∠1−∠2，理由如下：
如图①，过点P作PM/​/AB，
∵AB/​/CD，
∴AB/​/CD/​/PM，
∴∠1+∠EPM=180°，∠2+∠MPF=180°，
∴∠EPM=180°−∠1，∠MPF=180°−∠2，
∴∠EPF=∠EPM+∠MPF=(180°−∠1)+(180°−∠2)=360°−∠1−∠2；
(3)如图②，过点P作PM/​/AB，
∵AB/​/CD，
∴AB/​/CD/​/PM，
由(2)知，∠PGF=360°−∠MPG−∠2，
∵PM/​/AB，
∴∠1+∠EPM=180°，
∴∠EPM=180°−∠1，
∵∠EPG=∠EPM+∠MPG=75°，
∴∠MPG=75°−∠EPM=75°−(180°−∠1)=∠1−105°，
∴∠PGF=360°−∠MPG−∠2=360°−(∠1−105°)−∠2=465°−(∠1+∠2)，
∵∠1+∠2=325°，
∴∠PGF=465°−325°=140°．
【解析】解：(1)如图①，过点P作PM/​/AB，
∵AB/​/CD，
∴AB/​/CD/​/PM，
∴∠1+∠EPM=180°，∠2+∠MPF=180°，
∵∠1=130°，∠2=150°，
∴∠EPM=50°，∠MPF=30°，
∴∠EPF=∠EPM+∠MPF=50°+30°=80°，
故答案为：80；
(2)见答案；
(3)见答案．
(1)过点P作PM/​/AB，根据平行线的性质即可求解；
(2)过点P作PM/​/AB，根据平行线的性质即可求解；
(3)过点P作PM/​/AB，结合(2)再根据平行线的性质即可求解．
本题考查了平行线的判定与性质，熟记平行线的判定与性质并作恰当的辅助线是解题的关键．