浙江省杭州市上城区2021-2022学年五年级下学期期末数学试卷

这是一份浙江省杭州市上城区2021-2022学年五年级下学期期末数学试卷，共15页。试卷主要包含了填空题，选择题，计算题，操作题，填空，解决问题等内容，欢迎下载使用。

1．（2分）在4、4.5、7、19、21、87这些数中， 是 的倍数； 和 是质数。
2．（2分） ÷6＝＝6÷
3．（2分）12和15的最大公因数是 ，最小公倍数是 ．
4．（2分）一个粉笔盒的体积大约是0.8
2050mL＝ cm3
5．（2分）在数轴上表示出和1.75的位置。
​
6．（2分）一个棱长为1dm的正方体容器中装满了水，放入一块鹅卵石后再取出，发现水面下降了3cm，可知鹅卵石的体积是 cm3。
7．（2分）如图是由棱长1cm的小正方体搭成，这个图形的体积是 cm3，表面积是 m2。
​
8．（2分）一根8米长的绳子，第一次用去全长的，第二次用去2米，算式+2÷8，可以算出 。
9．（2分）小明有9根4cm的小棒和6根7cm的小棒，他用其中的12根小棒搭成了一个长方体框架。这个长方体框架的棱长和是 cm。
二、选择题（每题2分，共14分）
10．（2分）已知两个非0自然数M与N有如下关系：M＝6N，则M与N的最大公因数是（ ）
A．MB．NC．6D．1
11．（2分）一个巧克力礼盒，重2kg，装有12块，平均分给4个小朋友，每个小朋友分到这盒巧克力的（ ）
A．B．C．D．
12．（2分）下列几何体中，不符合如图要求的是（ ）
​
A．B．
C．D．
13．（2分）A、B是两个连续自然数，且都不等于0，它们相乘的积一定是（ ）
A．奇数B．偶数C．质数D．合数
14．（2分）如图是一个长方体，左面面积是21cm2，后面用棱长1cm的小正方体铺满，根据已知信息，这个长方体的体积是（ ）cm3。
​
A．63B．126C．147D．378
15．（2分）从一块长方体木块中如图那样挖去一个小正方体，它的体积减少了，表面积（ ）
A．减少了B．增加了C．不变D．无法判断
16．（2分）从0、2、4、6、8这几张卡片中选择三张卡片排成一个三位数，使它是2、3、5的倍数，可以组成（ ）个。
A．2B．4C．6D．8
三、计算题（共22分）
17．（4分）直接写出得数。
18．（12分）用合理的方法计算。（请写出主要的计算过程）
19．（6分）解方程。
x﹣＝
＝1.8
+x÷2＝0.5
四、操作题（共6分）
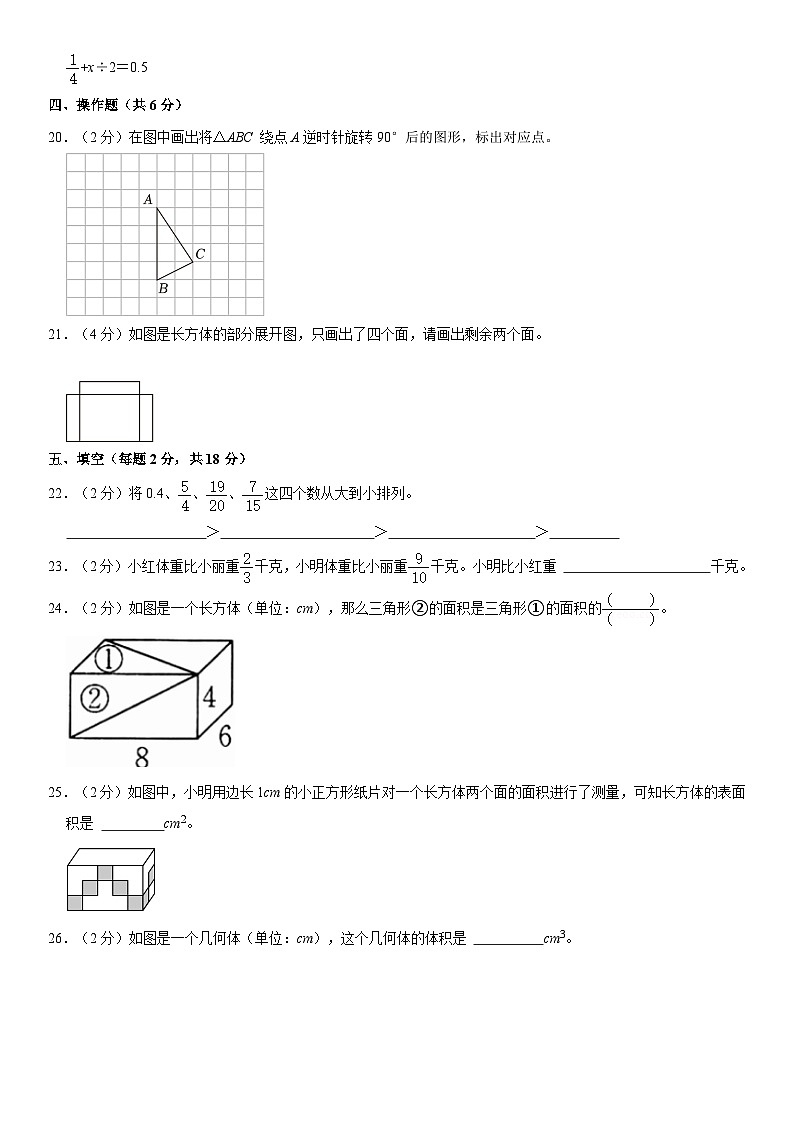
20．（2分）在图中画出将△ABC 绕点A逆时针旋转90°后的图形，标出对应点。
​
21．（4分）如图是长方体的部分展开图，只画出了四个面，请画出剩余两个面。
​
五、填空（每题2分，共18分）
22．（2分）将0.4、、、这四个数从大到小排列。
＞ ＞ ＞
23．（2分）小红体重比小丽重千克，小明体重比小丽重千克。小明比小红重 千克。
24．（2分）如图是一个长方体（单位：cm），那么三角形②的面积是三角形①的面积的。
​
25．（2分）如图中，小明用边长1cm的小正方形纸片对一个长方体两个面的面积进行了测量，可知长方体的表面积是 cm2。
26．（2分）如图是一个几何体（单位：cm），这个几何体的体积是 cm3。
​
27．（2分）已知：A＝4×999+5×99+6×9+（4+5+9），
B＝2×999+4×99+8×9+（2+4+8+5），
C＝2×1000+2×100+3×10+6。
那么A、B、C三个数中， 是3的倍数。
28．（2分）某校为增加同学们的阅读量，这几年大量购进图书，如图是该校2018～2021年的学生总人数和人均占有图书册数的统计图。
该校图书馆2021年比2018年藏书量增加了 册。
29．（2分）同样大小的两个正方形面积都为1，分别如图平均分。如果将两个正方形如图重叠，那么这个图形的面积用最简分数表示是 。
​
30．（2分）在下面9个方格中填上数，使得每个横行、竖行、斜行三个数的和都相等，这样的九宫格我们叫做“三阶幻方”。为了完成幻方，A处应填 ，B处应填 。
六、解决问题（共22分）
31．（4分）一节体育课共40分钟，分准备活动、正式活动、放松运动三个环节。准备活动用了整节课的，放松运动用了8分钟，那么正式活动时间占整节课的几分之几？
32．（4分）一杯纯牛奶，乐乐先喝了杯，兑满水之后又喝了半杯。乐乐两次喝了多少杯纯牛奶？
33．（4分）一个长方形，尺寸如图，如果将它分割成一些大小相同的小正方形，并希望正方形边长是整厘米数，请问共有多少种不同的分法？这个长方形最少可以分多少个小正方形？
34．（4分）1箱糖果有7袋，我们将这7袋糖果分别用序号①～⑦表示，其中6袋质量相同，另有一袋质量不足，如果用天平称，至少称几次能保证找出这袋糖果？请你表示出用天平找次品的过程。
35．（6分）有一个密闭的长方体容器，如图，容器中有一些水，深度为12cm。现在将这个容器右侧面着地。
（1）此时水面高度是多少cm？
（2）此时水面和这个容器接触的面积是多少cm2？
2021-2022学年浙江省杭州市上城区五年级（下）期末数学试卷
参考答案与试题解析
一、填空题（每题2分，共18分）
1．【分析】若整数a能够被b整除，a叫做b的倍数，b就叫做a的因数，因数与倍数是相互依存的，据此解答。
一个数，如果只有1和它本身两个约数，这样的数叫做质数（或素数）；一个数，如果除了1和它本身还有别的约数，这样的数叫做合数。
【解答】解：在4、4.5、7、19、21、87这些数中，21是 7的倍数；7和19是质数。
故答案为：21，7；7，19。
2．【分析】根据分数与除法的关系＝9÷12，再根据商不变的性质被除数、除数都除以2就是4.5÷6；被除数就是6÷8。
【解答】解：4.5÷6＝＝6÷8
故答案为：4.5，8。
3．【分析】根据求两个数最大公约数也就是这两个数的公有质因数的连乘积，最小公倍数是公有质因数与独有质因数的连乘积求解．
【解答】解：12＝2×2×3
15＝3×5
所以12和15的最大公因数是3，最小公倍数是3×2×2×5＝60；
故答案为：3，60．
4．【分析】根据生活经验以及对体积单位和数据大小的认识，结合实际情况选择合适的单位即可。
毫升和立方厘米，二者互化数值不变；据此解答。
【解答】解：一个粉笔盒的体积大约是0.8立方分米
2050mL＝2050cm3
故答案为：立方分米，2050。
5．【分析】根据数轴的认识即可解答。
【解答】解：
6．【分析】这块鹅卵石的体积等于下降的水的体积，用底面积乘下降的厘米数即可。
【解答】解：1分米＝10厘米
10×10×3
＝100×3
＝300（立方厘米）
答：鹅卵石的体积是300cm3。
故答案为：300。
7．【分析】数出小正方体的个数，用个数乘每个小正方体的体积，求总体积即可；
数出几何体露在外面的小正方体面的个数，乘每个面的面积即可。
【解答】解：1×1×1×10＝10（立方厘米）
（5+4+6）×2×（1×1）
＝15×2×1
＝30（平方厘米）
答：这个图形的体积是10cm3，表面积是30m2。
故答案为：10；30。
8．【分析】求一个数是另一个数的几分之几，用这个数除以另一个数，由此可知2÷8表示第二次用去全长的几分之几，再加上第一次用去的，就是两次一共用去全长的几分之几。
【解答】解：算式+2÷8，可以算出两次一共用去全长的几分之几。
故答案为：两次一共用去全长的几分之几。
9．【分析】根据长方体的特征，12条棱分为互相平行的（相对的）3组，每组4条棱的长度相等，长方体的棱长总和＝（长+宽+高）×4。
【解答】解：（4+4+7）×4
＝15×4
＝60（厘米）
答：这个长方体框架的棱长和是60cm。
故答案为：60。
二、选择题（每题2分，共14分）
10．【分析】两个数为倍数关系，则最大公因数是较小的数。据此解答。
【解答】解：因为M＝6N，M÷N＝6，所以M与N的最大公因数是N。
故选：B。
11．【分析】把一个巧克力礼盒看作整体“1”，平均分给4个小朋友，其中1个小朋友分到其中的，据此解答。
【解答】解：1
因此每个小朋友分到这盒巧克力的。
故选：A。
12．【分析】分别从正面和左面观察所给几何体，根据看到的形状选择即可。
【解答】解：不符合如图要求的是。
故选：C。
13．【分析】自然数根据是否是2的倍数可分为偶数与奇数两类，根据自然数排列规律，相邻的两个自然数中，一定有一个奇数，一个偶数，根据数的奇偶性可知，奇数×偶数＝偶数，所以两个连续的自然数（非0）的积一定是偶数。
【解答】解：两个连续的自然数中一定有一个奇数，一个偶数，
根据数的奇偶性可知，奇数×偶数＝偶数，
所以两个连续的自然数（非0）的积一定是偶数。
故选：B。
14．【分析】根据左面面积是21cm2，可知长方体高是21÷7＝3（cm），后面用棱长1cm的小正方体铺满，后面面积是6×3＝18（cm2），长方体的长是18÷3＝6（cm），再根据长方体体积＝长×宽×高即可解答。
【解答】解：21÷7＝3（cm）
18÷3＝6（cm）
6×7×3
＝42×3
＝126（cm3）
答：这个长方体的体积是126cm3。
故选：B。
15．【分析】通过观察图形可知，在长方体中的小正方体原来外露3个面，从长方体中挖掉一个小正方体后，又外露与原来相同的3个面，所以剩下图形的表面积与原来的表面积相等。据此解答。
【解答】解：从一块长方体木块中如图那样挖去一个小正方体，它的体积减少了，表面积不变。
故选：C。
16．【分析】这个数是2和5的倍数，个位数只能是0，十位上和百位上的数字相加的和能被3整除，那么这个三位数就可以是2、3、5的倍数。
【解答】解：从0、2、4、6、8这几张卡片中选择三张卡片排成一个三位数，使它是2、3、5的倍数，有240、420、480、840。
故选：B。
三、计算题（共22分）
17．【分析】根据分数、小数加减法的计算方法进行计算；被减数＝差+减数。
【解答】解：
18．【分析】（1）按照加法交换律计算；
（2）按照加法结合律计算；
（3）按照减法的性质计算；
（4）按照从左到右的顺序计算；
（5）按照减法的性质计算；
（6）按照加法交换律和结合律计算。
【解答】解：（1）
＝++
＝1+
＝1
（2）
＝+（﹣）
＝+
＝
（3）﹣（+）
＝﹣﹣
＝1﹣
＝
（4）﹣0.25
＝+
＝
（5）0.7
＝0.7﹣（+）
＝0.7﹣
＝0.2
（6）+0.3
＝（﹣）+（0.3+）
＝+1
＝1
19．【分析】根据等式的性质，方程两边同时加上求解；
根据等式的性质，方程两边同时减去，然后再同时乘5求解；
根据等式的性质，方程两边同时减去，然后再同时乘2求解。
【解答】解：x﹣＝
x﹣+＝+
x＝
＝1.8
+﹣＝1.8﹣
＝1
×5＝1×5
x＝5
+x÷2＝0.5
+x÷2﹣＝0.5﹣
x÷2＝0.25
x÷2×2＝0.25×2
x＝0.5
四、操作题（共6分）
20．【分析】根据旋转的特征，△ABC 绕点A逆时针旋转90°，点A的位置不动，这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形并标出对应点。
【解答】解：
21．【分析】根据长方体的特征：相对的面完全相等，据此作图即可。
【解答】解：如图：
五、填空（每题2分，共18分）
22．【分析】把分数化成小数，再按小数大小比较的方法进行比较。
【解答】解：
因为1.25＞0.95＞0.47＞0.4，所以＞0.4。
故答案为：＞0.4。
23．【分析】求小明比小红重多少千克，就是求千克与千克的差。据此解答。
【解答】解：﹣＝（千克）
答：小明比小红重千克。
故答案为：。
24．【分析】根据三角形面积＝底×高÷2，求出两个三角形面积，再根据除法意义用三角形②的面积除以三角形①的面积即可解答。
【解答】解：三角形②的面积是：
8×4÷2
＝32÷2
＝16（cm2）
三角形①的面积是：
8×6÷2
＝48÷2
＝24（cm2）
16÷24＝
答：三角形②的面积是三角形①的面积的。
故答案为：2，3。
25．【分析】通过观察图形可知，这个长方体的长是5厘米，宽是2厘米，高是3厘米，根据长方体的表面积公式：S＝（ab+ah+bh）×2，把数据代入公式解答。
【解答】解：（5×2+5×3+2×3）×2
＝（10+15+6）×2
＝31×2
＝62（平方厘米）
答：这个长方体的表面积是62平方厘米。
故答案为：62。
26．【分析】由图可知，这个几何体的横截面是一个梯形，用梯形的面积乘这个几何体的长，即可求出这个几何体的体积。
【解答】解：（4+6）×5÷2×15
＝25×15
＝375（立方厘米）
答：这个几何体的体积是375立方厘米。
故答案为：375。
27．【分析】根据3的倍数的特征：各个数位上数的和是3的倍数，这个数就是3的倍数。据此解答。
【解答】解：9是3的倍数
4×999、5×99、6×9、4+5+9都是3的倍数，所以A的3的倍数。
故答案为：A。
28．【分析】根据总量＝平均数×数量，分别求出2021年和2018的藏书量，用2021年藏书量减去2018年藏书量即可解答。
【解答】解：25×2400﹣15×1200
＝60000﹣18000
＝42000（册）
答：该校图书馆2021年比2018年藏书量增加了42000册。
故答案为：42000。
29．【分析】根据题意可知，每个正方形面积都为1，两个正方形面积一共为2。将这两个正方形重叠后，重叠部分面积为，用两个正方形面积和减去重叠部分，即为该图形的面积。据此解答。
【解答】解：1+1﹣
＝2﹣
＝
答：这个图形的面积用最简分数表示是。
故答案为：。
30．【分析】根据奇阶幻方的特征可知，+A＝+1.6，则A＝+1.6﹣，求出A的值，则B就是1.6与A的平均数，据此解答即可。
【解答】解：A＝+1.6﹣＝0.4
B＝（1.6+0.4）÷2＝1
答：A处应填0.4，B处应填1。
故答案为：0.4；1。
六、解决问题（共22分）
31．【分析】用放松运动用的时间除以一节体育课的总时间，即可计算出放松运动占这节课的几分之几，再用单位“1”减去准备活动用了整节课的分率，再减去放松运动时间占这节课时间的分率，即可计算出正式活动时间占整节课的几分之几。
【解答】解：
＝
＝
答：正式活动时间占整节课的。
32．【分析】由题意可知，乐乐第二次喝了杯牛奶的一半，也就是杯牛奶；用先喝的杯加上后喝的杯，即可求出乐乐两次喝了多少杯纯牛奶。
【解答】解：1﹣＝（杯）
乐乐第二次喝了杯牛奶的一半，也就是杯牛奶。
+＝（杯）
答：乐乐两次喝了杯纯牛奶。
33．【分析】只要把它截成正方形纸片，则这个正方形纸片的边长应为长方形长与宽的公因数，找出18和24的公因数，即可得共有多少种不同的分法；18和24的最大公因数就是最大正方形的边长，用18和24分别除以最大正方形的边长，得到的数字相乘就是最少可以裁成的正方形个数，因此得解。
【解答】解：18＝2×3×3
24＝2×2×2×3
18和24个公因数有1、2、3、6，共4个。
18和24的最大公因数是2×3＝6
（18÷6）×（24÷6）
＝3×4
＝12（个）
答：共有4种不同的分法，这个长方形最少可以分12个小正方形。
34．【分析】根据图示，把7袋糖果分成三份（3袋、3袋、1袋），取3袋的两份分别放在天平两侧，若天平平衡，则未取的1袋为较轻的，若天平不平衡，取较轻的一份继续；第二次取较轻的一份（3袋）中的2袋分别放在天平两侧，若天平平衡，则未取的一袋为次品，若天平不平衡，可找到较轻的。据此做题。
【解答】解：如图：
答：至少称2次能保证找出这袋糖果。
35．【分析】（1）根据长方体的体积公式V＝abh，求出长方体玻璃箱内水的体积，由于容器内水的体积不变，把容器的左面作为底面，所以用水的体积除以左面那个面的底面积就是水面的高度；
（2）水与容器的接触面的面积就是长2分米，宽1分米，高为此时水深的长方体5个面的面积，缺少上面，根据长方体的表面积解答即可。
【解答】解：（1）6分米＝60厘米
3分米＝30厘米
2分米＝20厘米
60×20×12÷（20×30）
＝14400÷600
＝24（厘米））
答：这时水深24厘米。
（2）30×20+20×24×2+30×24×2
＝600+960+1440
＝3000（cm2）
答：水与容器的接触面积是3000cm2。＝
＝
＝
﹣0.25＝
1﹣＝
＝
﹣＝1.4
4﹣＝
﹣（+）
﹣0.25
0.7
+0.3
1.6
B
A
＝
＝
＝
﹣0.25＝
1﹣＝
＝
1.8﹣＝1.4
4﹣＝3