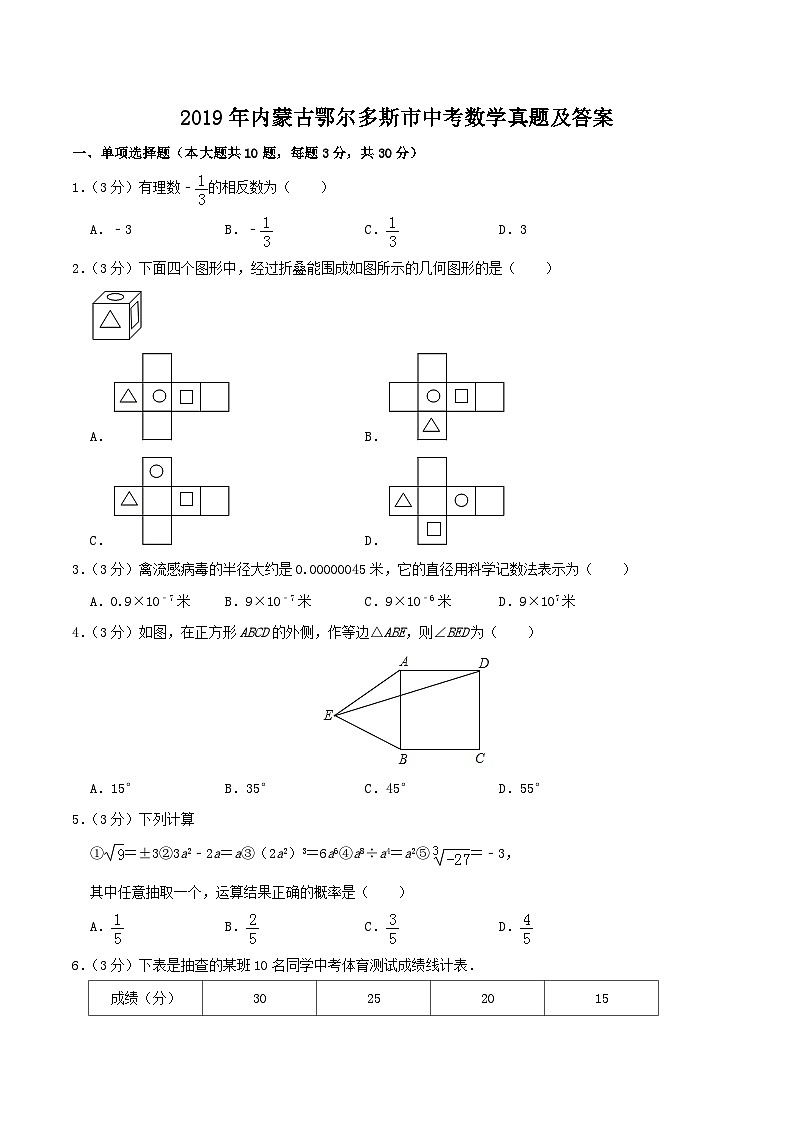
2019年内蒙古鄂尔多斯市中考数学真题及答案

这是一份2019年内蒙古鄂尔多斯市中考数学真题及答案，共23页。试卷主要包含了单项选择题，填空题，解答题等内容，欢迎下载使用。

1．（3分）有理数﹣的相反数为（ ）
A．﹣3B．﹣C．D．3
2．（3分）下面四个图形中，经过折叠能围成如图所示的几何图形的是（ ）
A．B．
C．D．
3．（3分）禽流感病毒的半径大约是0.00000045米，它的直径用科学记数法表示为（ ）
A．0.9×10﹣7米B．9×10﹣7米C．9×10﹣6米D．9×107米
4．（3分）如图，在正方形ABCD的外侧，作等边△ABE，则∠BED为（ ）
A．15°B．35°C．45°D．55°
5．（3分）下列计算
①＝±3②3a2﹣2a＝a③（2a2）3＝6a6④a8÷a4＝a2⑤＝﹣3，
其中任意抽取一个，运算结果正确的概率是（ ）
A．B．C．D．
6．（3分）下表是抽查的某班10名同学中考体育测试成绩线计表．
若成绩的平均数为23，中位数是a，众数是b，则a﹣b的值是（ ）
A．﹣5B．﹣2.5C．2.5D．5
7．（3分）如图，在▱ABCD中，∠BDC＝47°42′，依据尺规作图的痕迹，计算α的度数是（ ）
A．67°29′B．67°9′C．66°29′D．66°9′
8．（3分）下列说法正确的是（ ）
①函数y＝中自变量x的取值范围是x≥．
②若等腰三角形的两边长分别为3和7，则第三边长是3或7．
③一个正六边形的内角和是其外角和的2倍．
④同旁内角互补是真命题．
⑤关于x的一元二次方程x2﹣（k+3）x+k＝0有两个不相等的实数根．
A．①②③B．①④⑤C．②④D．③⑤
9．（3分）如图，矩形ABCD与菱形EFGH的对角线均交于点O，且EG∥BC，将矩形折叠，使点C与点O重合，折痕MN过点G．若AB＝，EF＝2，∠H＝120°，则DN的长为（ ）
A．B．C．D．2
10．（3分）在“加油向未来”电视节目中，王清和李北进行无人驾驶汽车运送货物表演，王清操控的快车和李北操控的慢车分别从A，B两地同时出发，相向而行．快车到达B地后，停留3秒卸货，然后原路返回A地，慢车到达A地即停运休息，如图表示的是两车之间的距离y（米）与行驶时间x（秒）的函数图象，根据图象信息，计算a、b的值分别为（ ）
A．39，26B．39，26.4C．38，26D．38，26.4
二、填空题（本大题共6题，每题3分，共18分）
11．（3分）计算：（π+1）0+|﹣2|﹣（）﹣2＝ ．
12．（3分）一组数据﹣1，0，1，2，3的方差是 ．
13．（3分）如图，△ABC中，AB＝AC，以AB为直径的⊙O分别与BC，AC交于点D，E，连接DE，过点D作DF⊥AC于点F．若AB＝6，∠CDF＝15°，则阴影部分的面积是 ．
14．（3分）如果三角形有一边上的中线长等于这边的长，那么称这个三角形为“好玩三角形”．若Rt△ABC是“好玩三角形”，且∠A＝90°，则tan∠ABC＝ ．
15．（3分）如图，有一条折线A1B1A2B2A3B3A4B4…，它是由过A1（0，0），B1（4，4），A2（8，0）组成的折线依次平移8，16，24，…个单位得到的，直线y＝kx+2与此折线有2n（n≥1且为整数）个交点，则k的值为 ．
16．（3分）如图，在圆心角为90°的扇形OAB中，OB＝2，P为上任意一点，过点P作PE⊥OB于点E，设M为△OPE的内心，当点P从点A运动到点B时，则内心M所经过的路径长为 ．
三、解答题（本大题共8题，共72分，解答时写出必要的文字说明，演算步骤或推理过程）
17．（8分）（1）先化简：+÷，再从﹣1≤x≤3的整数中选取一个你喜欢的x的值代入求值．
（2）解不等式组，并写出该不等式组的非负整数解．
18．（9分）某校调查了若干名家长对“初中生带手机上学”现象的看法，统计整理并制作了如下的条形与扇形统计图，根据图中提供的信息，完成以下问题：
（1）本次共调查了 名家长，扇形统计图中“很赞同”所对应的圆心角度数是 度，并补全条形统计图．
（2）该校共有3600名家长，通过计算估计其中“不赞同”的家长有多少名？
（3）从“不赞同”的五位家长中（两女三男），随机选取两位家长对全校家长进行“学生使用手机危害性”的专题讲座，请用树状图或列表法求出选中“1男1女”的概率．
19．（8分）教室里的饮水机接通电源就进入自动程序，开机加热时每分钟上升10℃，加热到100℃停止加热，水温开始下降，此时水温y（℃）与开机后用时x（min）成反比例关系，直至水温降至30℃，饮水机关机，饮水机关机后即刻自动开机，重复上述自动程序．若在水温为30℃时接通电源，水温y（℃）与时间x（min）的关系如图所示：
（1）分别写出水温上升和下降阶段y与x之间的函数关系式；
（2）怡萱同学想喝高于50℃的水，请问她最多需要等待多长时间？
20．（7分）某校组织学生到恩格贝A和康镇B进行研学活动，澄澄老师在网上查得，A和B分
别位于学校D的正北和正东方向，B位于A南偏东37°方向，校车从D出发，沿正北方向前往A地，行驶到15千米的E处时，导航显示，在E处北偏东45°方向有一服务区C，且C位于A，B两地中点处．
（1）求E，A两地之间的距离；
（2）校车从A地匀速行驶1小时40分钟到达B地，若这段路程限速100千米/时，计算校车是否超速？
（参考数据：sin37°＝，cs37°＝，tan37°＝）
21．（8分）如图，AB是⊙O的直径，弦CD⊥AB，垂足为H，连接AC．过上一点E作EG∥AC交CD的延长线于点G，连接AE交CD于点F，且EG＝FG．
（1）求证：EG是⊙O的切线；
（2）延长AB交GE的延长线于点M，若AH＝2，CH＝2，求OM的长．
22．（9分）某工厂制作A，B两种手工艺品，B每天每件获利比A多105元，获利30元的A与获利240元的B数量相等．
（1）制作一件A和一件B分别获利多少元？
（2）工厂安排65人制作A，B两种手工艺品，每人每天制作2件A或1件B．现在在不增加工人的情况下，增加制作C．已知每人每天可制作1件C（每人每天只能制作一种手工艺品），要求每天制作A，C两种手工艺品的数量相等．设每天安排x人制作B，y人制作A，写出y与x之间的函数关系式．
（3）在（1）（2）的条件下，每天制作B不少于5件．当每天制作5件时，每件获利不变．若每增加1件，则当天平均每件获利减少2元．已知C每件获利30元，求每天制作三种手工艺品可获得的总利润W（元）的最大值及相应x的值．
23．（11分）（1）【探究发现】
如图1，∠EOF的顶点O在正方形ABCD两条对角线的交点处，∠EOF＝90°，将∠EOF绕点O旋转，旋转过程中，∠EOF的两边分别与正方形ABCD的边BC和CD交于点E和点F（点F与点C，D不重合）．则CE，CF，BC之间满足的数量关系是 ．
（2）【类比应用】
如图2，若将（1）中的“正方形ABCD”改为“∠BCD＝120°的菱形ABCD”，其他条件不变，当∠EOF＝60°时，上述结论是否仍然成立？若成立，请给出证明；若不成立，请猜想结论并说明理由．
（3）【拓展延伸】
如图3，∠BOD＝120°，OD＝，OB＝4，OA平分∠BOD，AB＝，且OB＞2OA，点C是OB上一点，∠CAD＝60°，求OC的长．
24．（12分）如图，抛物线y＝ax2+bx﹣2（a≠0）与x轴交于A（﹣3，0），B（1，0）两点，与y轴交于点C，直线y＝﹣x与该抛物线交于E，F两点．
（1）求抛物线的解析式．
（2）P是直线EF下方抛物线上的一个动点，作PH⊥EF于点H，求PH的最大值．
（3）以点C为圆心，1为半径作圆，⊙C上是否存在点M，使得△BCM是以CM为直角边的直角三角形？若存在，直接写出M点坐标；若不存在，说明理由．
2019年内蒙古鄂尔多斯市中考数学试卷
参考答案与试题解析
一、单项选择题（本大题共10题，每题3分，共30分）
1．【解答】解：有理数﹣的相反数为：．
故选：C．
2．【解答】解：三角形图案的顶点应与圆形的图案相对，而选项A与此不符，所以错误；
三角形图案所在的面应与正方形的图案所在的面相邻，而选项C与此也不符，
三角形图案所在的面应与圆形的图案所在的面相邻，而选项D与此也不符，正确的是B．
故选：B．
3．【解答】解：0.00000045×2＝9×10﹣7．
故选：B．
4．【解答】解：在正方形ABCD中，AB＝AD，∠BAD＝90°，
在等边△ABE中，AB＝AE，∠BAE＝∠AEB＝60°，
在△ADE中，AD＝AE，∠DAE＝∠BAD+∠BAE＝90°+60°＝150°，
所以，∠AED＝（180°﹣150°）＝15°，
所以∠BED＝∠AEB﹣∠AED＝60°﹣15°＝45°．
故选：C．
5．【解答】解：运算结果正确的有⑤，则运算结果正确的概率是，
故选：A．
6．【解答】解：∵平均数为23，
∴＝23，
∴25x+20y＝155，
即：5x+4y＝31，
∵x+y＝7，
∴x＝3，y＝4，
∴中位数a＝22.5，b＝20，
∴a﹣b＝2.5，
故选：C．
7．【解答】解：∵四边形ABCD为平行四边形，
∴AB∥CD，
∴∠ABD＝∠BDC＝47°42′，
由作法得EF垂直平分BD，BE平分∠ABD，
∴EF⊥BD，∠ABE＝∠DBE＝∠ABD＝23°51′，
∵∠BEF+∠EBD＝90°，
∴∠BEF＝90°﹣23°51°＝66°9′，
∴α的度数是66°9′．
故选：D．
8．【解答】解：①函数y＝中自变量x的取值范围是x＞﹣，故错误．
②若等腰三角形的两边长分别为3和7，则第三边长是7，故错误．
③一个正六边形的内角和是其外角和的2倍，正确．
④两直线平行，同旁内角互补是真命题，故错误．
⑤关于x的一元二次方程x2﹣（k+3）x+k＝0有两个不相等的实数根，正确，
故选：D．
9．【解答】解：延长EG交DC于P点，连接GC、FH；如图所示：
则CP＝DP＝CD＝，△GCP为直角三角形，
∵四边形EFGH是菱形，∠EHG＝120°，
∴GH＝EF＝2，∠OHG＝60°，EG⊥FH，
∴OG＝GH•sin60°＝2×＝，
由折叠的性质得：CG＝OG＝，OM＝CM，∠MOG＝∠MCG，
∴PG＝＝，
∵OG∥CM，
∴∠MOG+∠OMC＝180°，
∴∠MCG+∠OMC＝180°，
∴OM∥CG，
∴四边形OGCM为平行四边形，
∵OM＝CM，
∴四边形OGCM为菱形，
∴CM＝OG＝，
根据题意得：PG是梯形MCDN的中位线，
∴DN+CM＝2PG＝，
∴DN＝﹣；
故选：A．
10．【解答】解：速度和为：24÷（30﹣18）＝2米/秒，
由题意得：，解得：b＝26.4，
因此慢车速度为：＝0.8米/秒，快车速度为：2﹣0.8＝1.2米/秒，
快车返回追至两车距离为24米的时间：（26.4﹣24）÷（1.2﹣0.8）＝6秒，因此a＝33+6＝39秒．
故选：B．
二、填空题（本大题共6题，每题3分，共18分）
11．【解答】解：（π+1）0+|﹣2|﹣（）﹣2
＝1+2﹣﹣4
＝﹣1﹣
故答案为：﹣1﹣．
12．【解答】解：数据的平均数＝（﹣1+0+1+2+3）＝1，
方差s2＝[（﹣1﹣1）2+（0﹣1）2+（1﹣1）2+（2﹣1）2+（3﹣1）2]＝2．
故填2．
13．【解答】解：连接OE，
∵∠CDF＝15°，∠C＝75°，∴∠OAE＝30°＝∠OEA，
∴∠AOE＝120°，
S△OAE＝AE×OEsin∠OEA＝×2×OE×cs∠OEA×OEsin∠OEA＝，
S阴影部分＝S扇形OAE﹣S△OAE＝×π×32﹣＝3π﹣．
故答案3π﹣．
14．【解答】解：①如图1中，
在Rt△ABC中，∠A＝90°，CE是△ABC的中线，设AB＝EC＝2a，则AE＝EB＝a，AC＝a，
∴tan∠ABC＝＝．
②如图2中，
在Rt△ABC中，∠A＝90°，BE是△ABC的中线，设EB＝AC＝2a，则AE＝EC＝a，AB＝a，
∴tan∠ABC＝＝．，
故答案为：或．
15．【解答】解：∵A1（0，0），A2（8，0），A3（16，0），A4（24，0），…，
∴An（8n﹣8，0）．
∵直线y＝kx+2与此折线恰有2n（n≥1且为整数）个交点，
∴点An+1（8n，0）在直线y＝kx+2上，
∴0＝8nk+2，
解得：k＝﹣．
故答案为：﹣．
16．【解答】解：如图，以OB为斜边在OB的右边作等腰Rt△POB，以P为圆心PB为半径作⊙P，在优弧OB上取一点H，连接HB，HO，BM，MP．
∵PE⊥OB，
∴∠PEO＝90°，
∵点M是内心，
∴∠OMP＝135°，
∵OB＝OP，∠MOB＝∠MOP，OM＝OM，
∴△OMB≌△OMP（SAS），
∴∠OMB＝∠OMP＝135°，
∵∠H＝∠BPO＝45°，
∴∠H+∠OMB＝180°，
∴O，M，B，H四点共圆，
∴点M的运动轨迹是，
∴内心M所经过的路径长＝＝π，
故答案为π．
三、解答题（本大题共8题，共72分，解答时写出必要的文字说明，演算步骤或推理过程）
17．【解答】解：（1）+÷
＝
＝
＝，
当x＝3时，原式＝＝1；
（2），
由不等式①，得
x＜，
由不等式②，得
x≥﹣1，
故原不等式组的解集是﹣1≤x＜，
∴该不等式组的非负整数解是0，1．
18．【解答】解：（1）本次调查的家长人数为45÷22.5%＝200（人），
扇形统计图中“很赞同”所对应的圆心角度数是360°×＝27°，
不赞同的人数为200﹣（15+50+45）＝90（人），
补全图形如下：
故答案为：200、27；
（2）估计其中“不赞同”的家长有3600×＝1620（人）；
（3）用A表示男生，B表示女生，画图如下：
共有20种情况，一男一女的情况是12种，
则刚好抽到一男一女的概率是＝．
19．【解答】解：（1）由题意可得，
a＝（100﹣30）÷10＝70÷10＝7，
当0≤x≤7时，设y关于x的函数关系式为：y＝kx+b，
，得，
即当0≤x≤7时，y关于x的函数关系式为y＝10x+30，
当x＞7时，设y＝，
100＝，得a＝700，
即当x＞7时，y关于x的函数关系式为y＝，
当y＝30时，x＝，
∴y与x的函数关系式为：y＝，y与x的函数关系式每分钟重复出现一次；
（2）将y＝50代入y＝10x+30，得x＝2，
将y＝50代入y＝，得x＝14，
∵14﹣2＝12，﹣12＝
∴怡萱同学想喝高于50℃的水，请问她最多需要等待时间；
20．【解答】解：（1）如图，作CH⊥AD于H．
由题意∠HEC＝45°，可得CH＝EH，设CH＝HE＝x千米，
∵点C是AB的中点，CH∥BD，
∴AH＝HD＝（x+15）千米，
在Rt△ACH中，tan37°＝，
∴＝，
∴x＝45，
∴CH＝45（千米），AH＝60（千米），AD＝120（千米），
∴EA＝AD﹣DE＝120﹣15＝105（千米）．
（2）在Rt△ACH中，AC＝＝75（千米），
∴AB＝2AC＝150（千米），
∵150÷＝90千米/小时，
∵90＜100，
∴校车没有超速．
21．【解答】（1）证明：连接OE，如图，
∵GE＝GF，
∴∠GEF＝∠GFE，
而∠GFE＝∠AFH，
∴∠GEF＝∠AFH，
∵AB⊥CD，
∴∠OAF+∠AFH＝90°，
∴∠GEA+∠OAF＝90°，
∵OA＝OE，
∴∠OEA＝∠OAF，
∴∠GEA+∠OEA＝90°，即∠GEO＝90°，
∴OE⊥GE，
∴EG是⊙O的切线；
（2）解：连接OC，如图，
设⊙O的半径为r，则OC＝r，OH＝r﹣2，
在Rt△OCH中，（r﹣2）2+（2）2＝r2，解得r＝3，
在Rt△ACH中，AC＝＝2，
∵AC∥GE，
∴∠M＝∠CAH，
∴Rt△OEM∽Rt△CHA，
∴＝，即＝，
∴OM＝．
22．【解答】解：（1）设制作一件A获利x元，则制作一件B获利（105+x）元，由题意得：
，解得：x＝15，
经检验，x＝15是原方程的根，
当x＝15时，x+105＝120，
答：制作一件A获利15元，制作一件B获利120元．
（2）设每天安排x人制作B，y人制作A，则2y人制作C，于是有：
y+x+2y＝65，
∴y＝﹣x+
答：y与x之间的函数关系式为∴y＝﹣x+．
（3）由题意得：
W＝15×2×y+[120﹣2（x﹣5）]x+2y×30＝﹣2x2+130x+90y，
又∵y＝﹣x+
∴W＝﹣2x2+130x+90y＝﹣2x2+130x+90（﹣x+）＝﹣2x2+100x+1950，
∵W＝﹣2x2+100x+1950，对称轴为x＝25，而x＝25时，y的值不是整数，
根据抛物线的对称性可得：
当x＝26时，W最大＝﹣2×262+100×26+1950＝2198元．
此时制作A产品的13人，B产品的26人，C产品的26人，获利最大，最大利润为2198元．
23．【解答】解：（1）如图1中，结论：CE+CF＝BC．理由如下：
∵四边形ABCD是正方形，
∴AC⊥BD，OB＝OC，∠OBE＝∠OCF＝45°，
∵∠EOF＝∠BOC＝90°，
∴∠BOE＝∠OCF，
∴△BOE≌△COF（ASA），
∴BE＝CF，
∴CE+CF＝CE+BE＝BC．
故答案为CE+CF＝BC．
（2）如图2中，结论不成立．CE+CF＝BC．
理由：连接EF，在CO上截取CJ＝CF，连接FJ．
∵四边形ABCD是菱形，∠BCD＝120°，
∴∠BCO＝∠OCF＝60°，
∵∠EOF+∠ECF＝180°，
∴O，E，C，F四点共圆，
∴∠OFE＝∠OCE＝60°，
∵∠EOF＝60°，
∴△EOF是等边三角形，
∴OF＝FE，∠OFE＝60°，
∵CF＝CJ，∠FCJ＝60°，
∴△CFJ是等边三角形，
∴FC＝FJ，∠EFC＝∠OFE＝60°，
∴∠OFJ＝∠CFE，
∴△OFJ≌△EFC（SAS），
∴OJ＝CE，
∴CF+CE＝CJ+OJ＝OC＝BC，
（3）如图3中，由OB＞2OA可知△BAO是钝角三角形，∠BAO＞90°，作AH⊥OB于H，设OH＝x．
在Rt△ABH中，BH＝，
∵OB＝4，
∴+x＝4，
解得x＝（舍弃）或，
∴OA＝2OH＝1，
∵∠COD+∠ACD＝180°，
∴A，C，O，D四点共圆，
∵OA平分∠COD，
∴∠AOC＝∠AOD＝60°，
∴∠ADC＝∠AOC＝60°，
∵∠CAD＝60°，
∴△ACD是等边三角形，
由（2）可知：OC+OD＝OA，
∴OC＝1﹣＝．
24．【解答】解：（1）∵抛物线y＝ax2+bx﹣2（a≠0）与x轴交于A（﹣3，0），B（1，0）两点，
∴，
∴，
∴抛物线的解析式为y＝x2+x﹣2；
（2）如图1，过点P作直线l，使l∥EF，过点O作OP'⊥l，
当直线l与抛物线只有一个交点时，PH最大，等于OP'，
∵直线EF的解析式为y＝﹣x，
设直线l的解析式为y＝﹣x+m①，
∵抛物线的解析式为y＝x2+x﹣2②，
联立①②化简得，x2+x﹣2﹣m＝0，
∴△＝﹣4××（﹣2﹣m）＝0，
∴m＝﹣，
∴直线l的解析式为y＝﹣x﹣，
令y＝0，则x＝﹣，
∴M（﹣，0），
∴OM＝，
在Rt△OP'M中，OP'＝＝，
∴PH最大＝．
（3）①当∠CMB＝90°时，如图2，
∴BM是⊙O的切线，
∵⊙C半径为1，B（1，0），
∴BM2∥y轴，
∴∠CBM2＝∠BCO，M2（1，﹣2），
∴BM2＝2，
∵BM1与BM2是⊙C的切线，
∴BM1＝BM2＝2，∠CBM1＝∠BCM2，
∴∠CBM1＝∠BCO，∴BD＝CD，
在Rt△BOD中，OD2+OB2＝BD2，
∴OD2+1＝（2﹣OD）2，
∴OD＝，
∴BD＝，
∴DM1＝
过点M1作M1Q⊥y轴，
∴M1Q∥x轴，
∴△BOD∽△M1QD，
∴，
∴，
∴M1Q＝，DQ＝，
∴OQ＝+＝，
∴M1（﹣，﹣），
②当∠BCM＝90°时，如图3，
∴∠OCM3+∠OCB＝90°，
∵∠OCB+∠OBC＝90°，
∴∠OCM3＝∠OBC，
在Rt△BOC中，OB＝1，OC＝2，
∴tan∠OBC＝＝2，
∴tan∠OCM3＝2，
过点M3作M3H⊥y轴于H，
在Rt△CHM3中，CM3＝1，
设CH＝m，则M3H＝2m，
根据勾股定理得，m2+（2m）2＝1，
∴m＝，
∴M3H＝2m＝，OH＝OC﹣CH＝2﹣，
∴M3（﹣，﹣2），
而点M4与M3关于点C对称，
∴M4（，﹣﹣2），
即：满足条件的点M的坐标为（﹣，﹣）或（1，﹣2）或（﹣，﹣2）或（，﹣﹣2）．
成绩（分）
30
25
20
15
人数（人）
2
x
y
1