适用于老高考旧教材2024版高考数学二轮复习专题检测3立体几何文（附解析）

这是一份适用于老高考旧教材2024版高考数学二轮复习专题检测3立体几何文（附解析），共15页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1.已知圆锥的底面半径为1,其侧面展开图为一个半圆,则该圆锥的母线长为( )

A.B.C.2D.2
2.(2023贵州贵阳一模)棱锥的内切球半径R=,其中V锥,S锥分别为该棱锥的体积和表面积.如图为某三棱锥的三视图,若每个视图都是直角边长为1的等腰直角三角形,则该三棱锥内切球的半径为( )
A.B.C.D.
3.(2023四川南充二模)某三棱锥的三视图如图所示,已知它的体积为,则图中x的值为( )
A.1B.C.2D.2
4.某种药物呈胶囊形状,该胶囊中间部分为圆柱,左右两端均为半径为1的半球.已知该胶囊的表面积为10π,则它的体积为( )
A.B.
C.D.
5.(2023河北保定一模)设α,β是两个不同的平面,则“α内有无数条直线与β平行”是“α∥β”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
6.(2023陕西汉中二模)在三棱锥P-ABC中,PA⊥平面ABC,∠ABC=90°,AB=1,BC=,PA=2,则三棱锥P-ABC的外接球的表面积为( )
A.32πB.16π
C.8πD.12π
7.
(2023安徽宣城二模)中国某些地方举行婚礼时要在吉利方位放一张桌子,桌子上放一个装满粮食的升斗(如图),斗面用红纸糊住,斗内再插一杆秤、一把尺子,寓意为粮食满园、称心如意、十全十美.如图为一种婚庆升斗,把该升斗看作一个正四棱台,下底面边长为25 cm,上底面边长为10 cm,侧棱长为15 cm,忽略其壁厚,则该升斗的容积约为(参考数据:≈1.414,1 L=1 000 cm3)( )
A.1.5 LB.2.4 LC.3.4 LD.5.1 L
8.在正四棱锥P-ABCD中,侧棱与底面所成角的正切值为,若该正四棱锥的外接球的体积为π,则△PBD的面积为( )
A.2B.2C.2D.
9.已知一个圆柱的高是底面半径的2倍,且其上、下底面的圆周均在球面上,若球的体积为,则圆柱的体积为( )
A.16πB.8π
C.4πD.2π
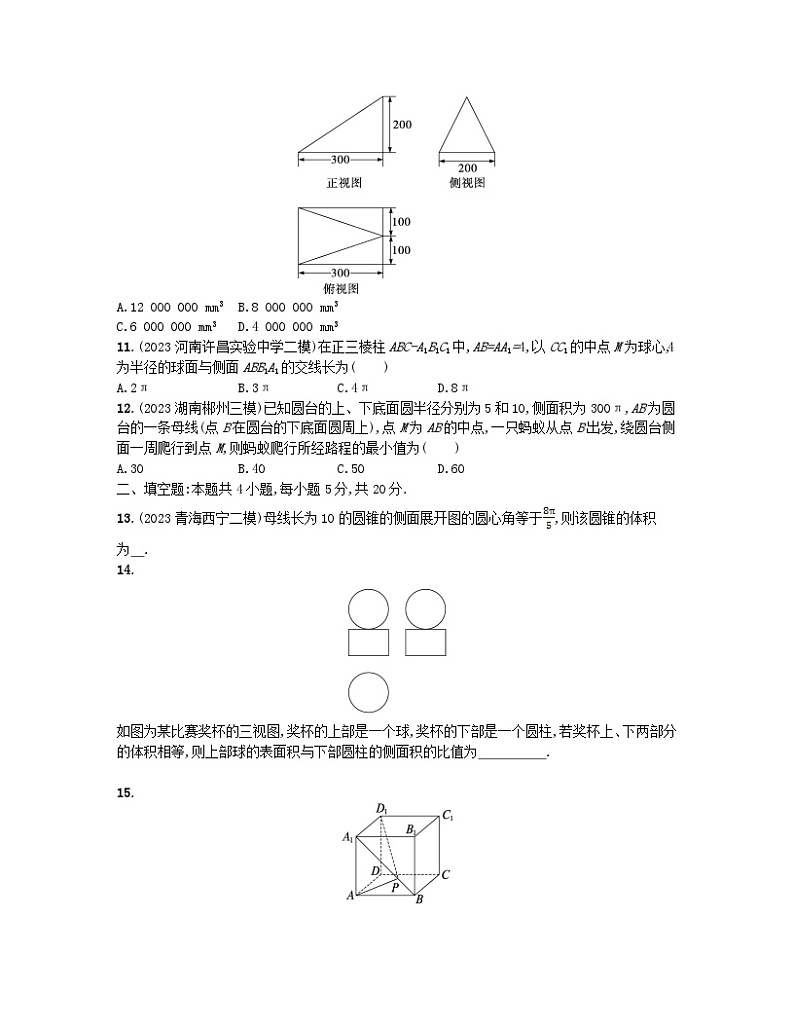
10.(2023广西桂林统考)如图,已知某个几何体的三视图,根据图中标出的尺寸(单位:mm),可得这个几何体的体积是( )
A.12 000 000 mm3B.8 000 000 mm3
C.6 000 000 mm3D.4 000 000 mm3
11.(2023河南许昌实验中学二模)在正三棱柱ABC-A1B1C1中,AB=AA1=4,以CC1的中点M为球心,4为半径的球面与侧面ABB1A1的交线长为( )
A.2πB.3πC.4πD.8π
12.(2023湖南郴州三模)已知圆台的上、下底面圆半径分别为5和10,侧面积为300π,AB为圆台的一条母线(点B在圆台的下底面圆周上),点M为AB的中点,一只蚂蚁从点B出发,绕圆台侧面一周爬行到点M,则蚂蚁爬行所经路程的最小值为( )
A.30B.40C.50D.60
二、填空题:本题共4小题,每小题5分,共20分.
13.(2023青海西宁二模)母线长为10的圆锥的侧面展开图的圆心角等于,则该圆锥的体积为 .
14.
如图为某比赛奖杯的三视图,奖杯的上部是一个球,奖杯的下部是一个圆柱,若奖杯上、下两部分的体积相等,则上部球的表面积与下部圆柱的侧面积的比值为 .
15.
如图,棱长为1的正方体ABCD-A1B1C1D1中,P为线段A1B上的动点(不含端点),则下列结论正确的是 .(填所有正确结论的序号)
①平面D1A1P⊥平面A1AP;
②∠APD1的取值范围是0,;
③三棱锥B1-D1PC的体积为定值;
④DC1⊥D1P.
16.(2023江西鹰潭一模)直四棱柱ABCD-A1B1C1D1的底面是菱形,其侧面积是8,若该直四棱柱有外接球,则该外接球的表面积的最小值为 .
三、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.
(10分)如图所示,在空间几何体ABCDE中,△ABC与△ECD均为等边三角形,AB=DE,且平面ABC和平面CDE均与平面BCD垂直.
(1)若,求证:平面ABC⊥平面ECD;
(2)求证:四边形AEDB为梯形.
18.(12分)
(2023江西景德镇、上饶联考)如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E,F,G分别为A1B1,BB1,C1D1的中点.
(1)过BG作该正方体的截面,使得该截面与平面C1EF平行,写出作法,并说明理由;
(2)设点M,N分别为棱AB,BC上一点,M,N与点B均不重合,且MN=C1F,求三棱锥B-B1MN体积的最大值.
19.(12分)(2023江西宜春4月模拟)如图1,在直角梯形ABCD中,AB∥CD,∠DAB=90°,CD=2AB=2AD=4,点E,F分别是边BC,CD的中点,现将△CEF沿EF边折起,使点C到达点P的位置(如图2所示),且BP=2.
图1
图2
(1)求证:平面APE⊥平面ABD;
(2)求点B到平面PAD的距离.
20.(12分)
(2023江西五市九校联考二)如图,在四棱锥P-ABCD中,四边形ABCD是平行四边形,PB⊥底面ABCD,BA=,AD=2,PB=,直线PD与平面ABCD所成角的正弦值为,点E,F分别是棱AD,PC的中点.
(1)求异面直线EF与AB所成角的正切值;
(2)求三棱锥P-ABD外接球的体积.
21.(12分)如图,四边形ABCD中,AB⊥AD,AD∥BC,AD=6,BC=2AB=4,E,F分别在BC,AD上,EF∥AB,现将四边形ABCD沿EF折起,使BE⊥EC.
(1)若BE=1,在折叠后的线段AD上是否存在一点P,使得CP∥平面ABEF?若存在,求出的值;若不存在,请说明理由.
(2)求三棱锥A-CDF的体积的最大值,并求出此时点F到平面ACD的距离.
22.(12分)(2023全国乙,文19)如图,在三棱锥P-ABC中,AB⊥BC,AB=2,BC=2,PB=PC=,BP,AP,BC的中点分别为D,E,O,点F在AC上,BF⊥AO.
(1)求证:EF∥平面ADO;
(2)若∠POF=120°,求三棱锥P-ABC的体积.
专题检测三 立体几何
1.C 解析依题意可知,半圆的弧长为2π·1=2π,圆心角的弧度数为π,由弧长公式可得该圆锥的母线长为=2.故选C.
2.C 解析由三视图可还原三棱锥如右图所示,其中PA⊥平面ABC,AB⊥AC,AB=AC=PA=1,设△ABC的面积是S△ABC,∴三棱锥P-ABC的体积是VP-ABC=S△ABC·PA=×1×1×1=.设△PBC的面积是S△PBC,设三棱锥的表面积S=3S△ABC+S△PBC=3××1×1+,∴该三棱锥的内切球半径R=.故选C.
3.
C 解析该三视图对应的直观图可以在棱长为2x的正方体中画出,即为三棱锥S-ABC,如图所示.
棱锥S-ABC的体积是V=××2x×2x×2x=,解得x=2.故选C.
4.C 解析设圆柱的高为h,
∴4π·12+2π·1·h=10π,
∴h=3.
∴V=π·13+π·12·3=.
故选C.
5.B 解析若α∩β=l,则α内存在无数条直线与l平行,这无数条除了l的直线显然平行于β,故充分性不成立;若α∥β,根据面面平行的定义可知,平面α内的直线都与平面β平行.所以,“α内有无数条直线与β平行”是“α∥β”的必要不充分条件.故选B.
6.
C 解析如图所示,根据题意可将三棱锥P-ABC补形为长方体,则三棱锥P-ABC的外接球即为长方体的外接球,可知该球的直径即为PC.设球的半径为R,可得2R==2,即R=,故三棱锥P-ABC的外接球的表面积S=4πR2=8π.故选C.
7.
C 解析上、下底面对角线的长度分别为10,25,则该正四棱台的高h=.上底面的面积S1=102=100(cm2),下底面的面积S2=252=625(cm2).则V=(S1+S2+)h=×(100+625+250)×≈3447cm3≈3.4L.故选C.
8.
A 解析当球心在线段PM上时,如图所示,令AC∩BD=M,四棱锥P-ABCD的外接球球心为O,设DM=x,OP=OD=R.由条件可知PM=x,在Rt△ODM中,R2=+x2,解得R=x.又πR3=π,得x=.所以DM=,PM=,所以△PBD的面积为×2=2.
容易验证球心O不在线段PM的延长线上.
综上,△PBD的面积是2.
9.C 解析设圆柱的底面圆半径为r,高为2r,球O的半径为R,
由题可知πR3=,解得R=2,
则r2+r2=R2=4,可得r=,
所以V=πr2·(2r)=4π.
故选C.
10.D 解析
由三视图可得几何体是四棱锥V-ABCD,其中平面VAB⊥平面ABCD.底面ABCD是边长分别为200mm和300mm的长方形,棱锥的高是200mm,
该棱锥的体积V=×200×300×200=4000000(mm3).
故选D.
11.C 解析由题意知该三棱柱的三个侧面都是边长为4的正方形.取AA1,BB1的中点分别为E,G,取点N为正方形ABB1A1的中心.
连接MN,ME,MG,EG.显然G,N,E三点共线.因为ME=MG,点N是EG的中点,所以MN⊥EG.因为ME∥AC,MG∥BC,所以BB1⊥MG,BB1⊥ME,又MG∩ME=M,MG,ME⊂平面MEG,所以BB1⊥平面MEG,所以BB1⊥MN.因为BB1∩EG=G,BB1,EG⊂平面ABB1A1,所以MN⊥平面ABB1A1.
所以点N为球与平面ABB1A1所得截面圆的圆心,该圆的半径为r==2,而正方形ABB1A1的边长为4,所以该圆是正方形ABB1A1的内切圆.所以所求交线为以点N为圆心,2为半径的圆,故交线长l=2×π×2=4π.故选C.
12.C 解析设圆台上底面半径为5,下底面半径为10,母线长为l,所以该圆台的侧面积为πl(10+5)=15πl=300π,解得l=20.
将圆台所在的圆锥展开如图所示,且设扇形的圆心为点O.线段B1M就是蚂蚁经过的最短距离.设OA=R,该扇形的圆心角是α,
则由题意知10π=αR①,20π=α(20+R)②,
由①②解得,α=,R=20,
所以OM=30,OB1=40,则B1M==50.故选C.
13.128π 解析由题意知圆锥的侧面展开图是一个扇形,该扇形的弧长为10×=16π.设圆锥的底面圆的半径为r,则2πr=16π,即r=8,该圆锥的高h==6,所以该圆锥的体积V=πr2h=π×82×6=128π.
14.
解析由三视图还原原几何体如图,设球的半径为R,圆柱的高为h,则由题意可得,πR3=πR2h,得h=R,球的表面积为S球=4πR2,圆柱的侧面积S圆柱侧=2πRh=2πR·R=πR2,∴上部球的表面积与下部圆柱的侧面积的比值为.
15.
①③④ 解析∵D1A1⊥平面A1AP,∴平面D1A1P⊥平面A1AP,①正确;
若P是A1B上靠近A1的一个四等分点,D1P2=1+2=,此时AP2=A+A1P2-2AA1×A1P×cs45°=,D1P2+AP20),由MN=C1F=,得a2+b2=5≥2ab,则ab≤,当且仅当a=b=时,等号成立.
ab×2=,因为ab≤,所以三棱锥B-B1MN体积的最大值为.
19.
(1)证明连接BD,BF,因为CD=2AB=4,点F是边CD的中点,所以DF=AB=2.因为AB∥CD,∠DAB=90°,所以四边形ABFD是矩形,又AD=2,所以矩形ABFD是正方形.所以BF=2,又CF=2,所以△BFC是等腰直角三角形,所以BC=2.因为点E是边BC的中点,则EF⊥BC.在折起后PE⊥EF.又BE2+PE2=()2+()2=4=BP2,所以PE⊥BE.又BE∩EF=E,BE⊂平面ABD,EF⊂平面ABD,故PE⊥平面ABD,又PE⊂平面APE,所以平面APE⊥平面ABD.
(2)解如图所示,取AD的中点O,连接OE,DE,PO,由(1)可知,PE⊥平面ABD,所以PE⊥DE,PE⊥AE,PE⊥OE.而OE=(AB+DC)=3,OD=AD=1,所以DE=,同理AE=,所以PD==2,PA==2,PO=.所以△PAD是等腰三角形,所以S△PAD=AD·PO=×2.设点B到平面PAD的距离是h,因为VB-PAD=VP-ABD,即S△PAD·h=S△ABD·PE,所以h=,即点B到平面PAD的距离为.
20.解(1)因为PB⊥底面ABCD,所以∠PDB为直线PD与平面ABCD所成的角.因为sin∠PDB=,即,又PB=,所以PD=,从而DB=.又BA=,AD=2,所以BA2+BD2=AD2,所以∠ABD=90°.
取BC的中点M,连接ME,MF.因为F是PC的中点,所以MF∥PB,且MF=PB=.又E是棱AD的中点,所以ME∥AB,且ME=AB=,从而∠FEM或其补角即为异面直线EF与AB所成的角.因为PB⊥底面ABCD,所以MF⊥底面ABCD,因为ME⊂底面ABCD,所以MF⊥ME,于是tan∠FEM=.即异面直线EF与AB所成角的正切值为.
(2)在△ABD中,∠ABD=90°,所以三棱锥P-ABD的外接球即为以BA,BP,BD为三条邻边的长方体的外接球.设该外接球的半径为R,则2R=,所以球的体积为V=πR3=.
21.解(1)AD上存在一点P,使得CP∥平面ABEF,此时.理由如下,当时,,
如图,过点P作MP∥FD交AF于点M,连接ME,则,∵AF=BE=1,AD=6,∴FD=5,∴MP=3,又EC=3,MP∥FD∥EC,∴MP∥EC,故四边形MPCE为平行四边形,∴CP∥ME,又CP⊄平面ABEF,ME⊂平面ABEF,∴CP∥平面ABEF.
(2)设BE=x,则AF=x(0