


专题33 将军饮马模型 2024年中考数学核心几何模型重点突破(全国通用)
展开【模型1】两点一线
1.如图,在直线两侧各有一个定点,分别是点A、B,怎样在直线上找到一点P,使得PA+PB的值最小?
思路:由“两点间线段最短”可得当A、P、B三点共线时,PA+PB的值最小,即为AB的长度.
构图:连接AB,AB与的交点即为点P,如图所示:
2.如图,在直线同侧有A、B两个定点,怎样在直线上找到一点P,使得PA+PB的值最小?
构图:作点A关于的对称点A’,连接A’B,A’B与直线的交点即为点P,如图所示:
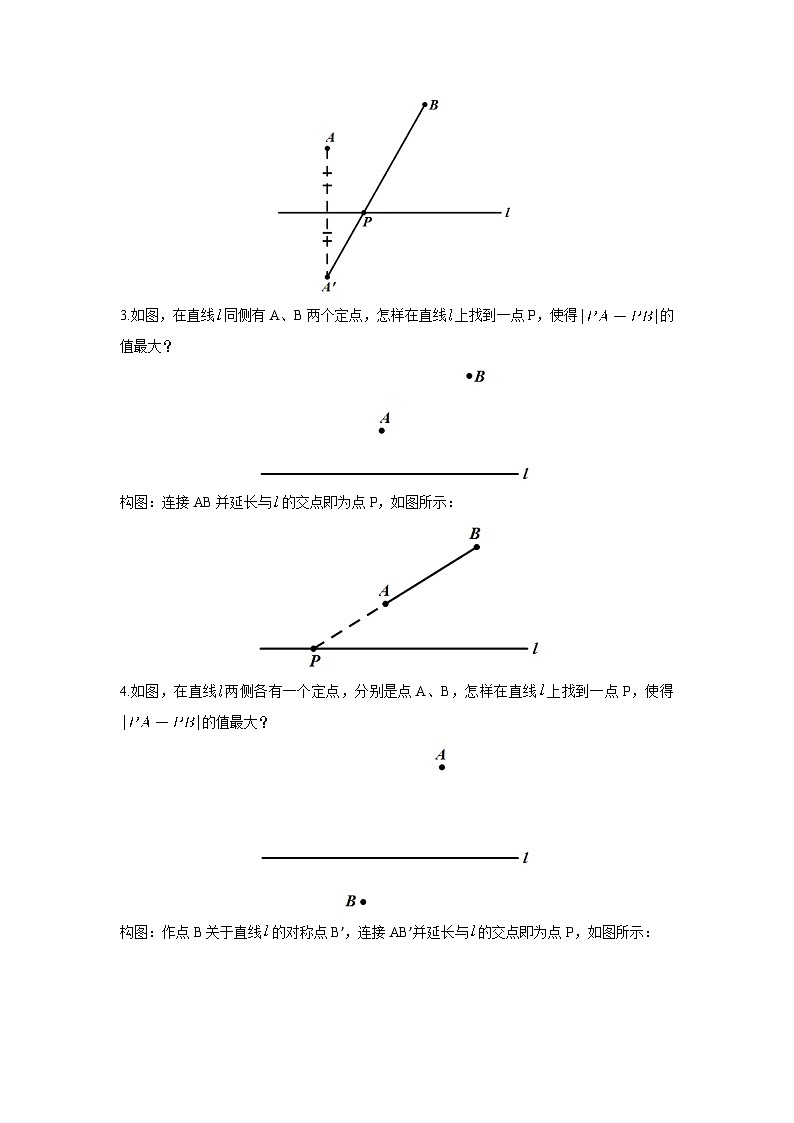
3.如图,在直线同侧有A、B两个定点,怎样在直线上找到一点P,使得的值最大?
构图:连接AB并延长与的交点即为点P,如图所示:
4.如图,在直线两侧各有一个定点,分别是点A、B,怎样在直线上找到一点P,使得的值最大?
构图:作点B关于直线的对称点B’,连接AB’并延长与的交点即为点P,如图所示:
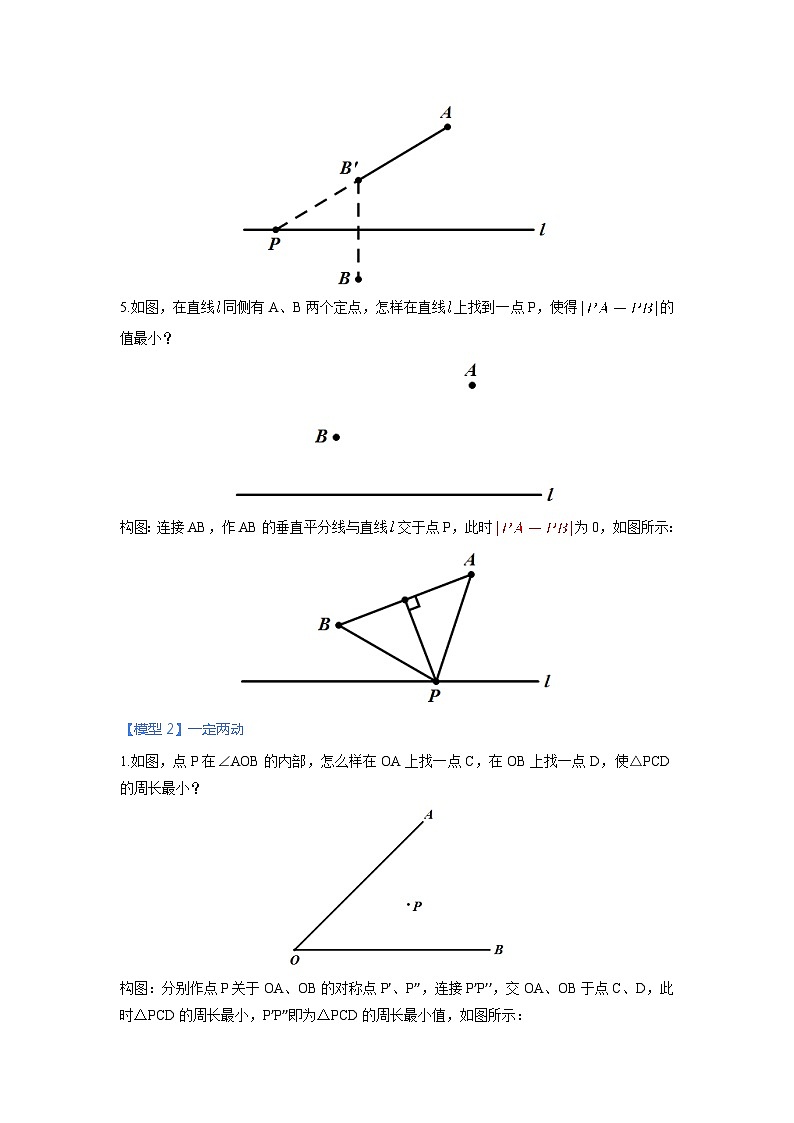
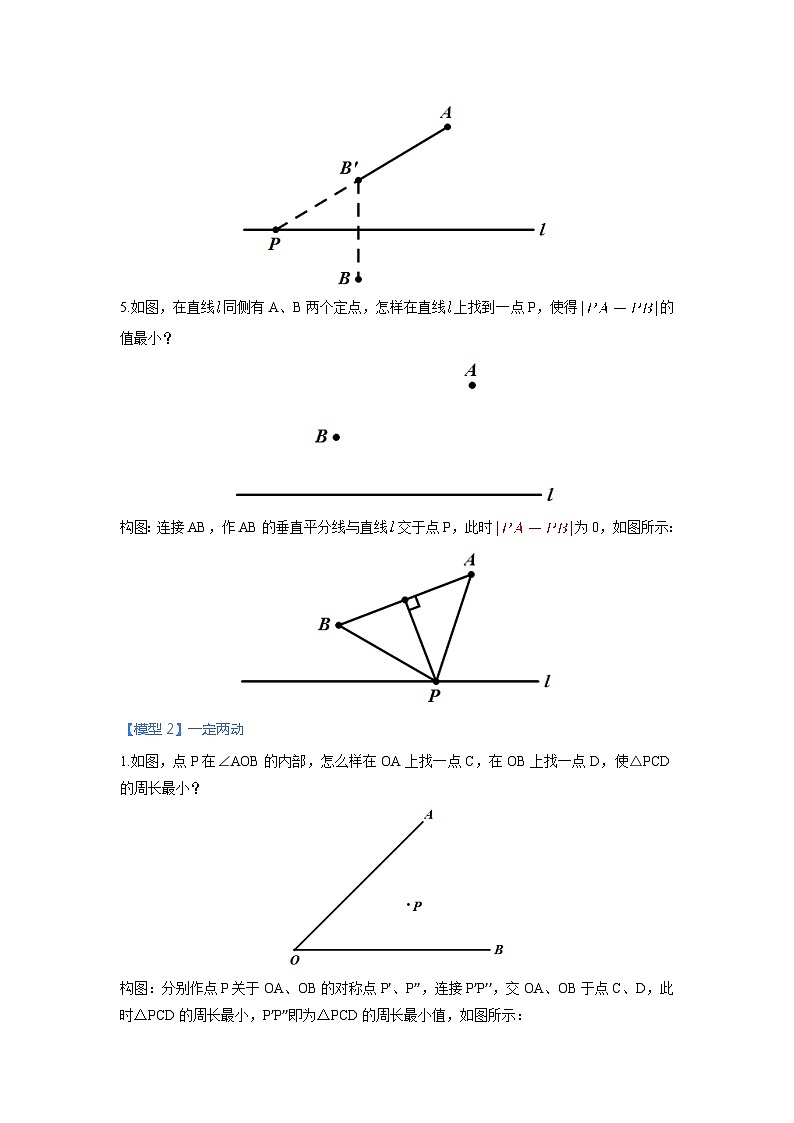
5.如图,在直线同侧有A、B两个定点,怎样在直线上找到一点P,使得的值最小?
构图:连接AB,作AB的垂直平分线与直线交于点P,此时为0,如图所示:
【模型2】一定两动
1.如图,点P在∠AOB的内部,怎么样在OA上找一点C,在OB上找一点D,使△PCD的周长最小?
构图:分别作点P关于OA、OB的对称点P’、P’’,连接P’P’’,交OA、OB于点C、D,此时△PCD的周长最小,P’P’’即为△PCD的周长最小值,如图所示:
2.如图,点P在∠AOB的内部,怎么样在OA上找一点C,在OB上找一点D,使PD+CD的值最小?
构图:作点P关于OB的对称点P’,过点P’作P’C⊥OA交OB于点D,交OA于点C,此时PD+CD的值最小,P’C即为PD+CD的值最小.
3.如图,点P在∠AOB的内部,怎样在OA、OB上分别取点C、D,使得△PCD的周长最小?
构图:分别作点P、Q关于OA、OB的对称点P’、Q’,连接P’Q’分别交OA、OB于点C、D,此时△PCD的周长最小值为PQ+P’Q’,如图所示:
【模型3】两点两线
在直线m、n上分别找两点P、Q,使得PA+PQ+QB的值最小.
1.A、B两点都在直线的外侧
2.一个点在内侧,一个点在外侧
3.两个点都在内侧
【例1】如图,正方形ABCD的边长为4,点M在DC上,且DM=1,N是AC上一动点,则DN+MN的最小值为( )
A.4B.C.D.5
【答案】D
【分析】由正方形的对称性可知点B与D关于直线AC对称,连接BM交AC于N′,N′即为所求在Rt△BCM中利用勾股定理即可求出BM的长即可.
【解析】∵四边形ABCD是正方形,
∴点B与D关于直线AC对称,
∴DN=BN,
连接BD,BM交AC于N′,连接DN′,
∴当B、N、M共线时,DN+MN有最小值,则BM的长即为DN+MN的最小值,
∴AC是线段BD的垂直平分线,
又∵CD=4,DM=1
∴CM=CD-DM=4-1=3,
在Rt△BCM中,BM=
故DN+MN的最小值是5.
故选:D.
【例2】如图,O为矩形ABCD对角线AC,BD的交点,AB=8,M,N是直线BC上的动点,且MN=2,则OM+ON的最小值是____________.
【答案】
【分析】根据题意,过O作OH∥BC,且令OH=2,连接NH,作O点关于BC的对称点K,连接OK,KH,则OM+ON= NH+ON= NH+ NK≥HK,当H、N、K三点共线的时候,OM+ON有最小值,最小值为HK的长.根据矩形性质及图形的对称性,易知,在中,运用勾股定理求得HK的长即可.
【解析】解:过O作OH∥BC,且令OH=2,连接NH,作O点关于BC的对称点K,连接OK,KH,
∵OH∥BC,OH=MN=2,
∴四边形OMNH是平行四边形,
∴OM=NH,
∴OM+ON= NH+ON.
∵O点关于BC的对称点是点K,
∴ON=NK,
∴OM+ON= NH+ON= NH+ NK,
∵,
∴当H、N、K三点共线的时候,OM+ON有最小值,最小值为HK的长.
∵OH∥BC,O点关于BC的对称点是点K,
∴.
∵O为矩形ABCD对角线AC,BD的交点,O点关于BC的对称点是点K,
∴OK=AB=8.
∵OH= 2,,
∴,
∴OM+ON的最小值是.
【例3】如图,在平面直角坐标系中,直线AB分别与x轴的负半轴、y轴的正半轴交于A、B两点,其中OA=2,S△ABC=12,点C在x轴的正半轴上,且OC=OB.
(1)求直线AB的解析式;
(2)将直线AB向下平移6个单位长度得到直线l1,直线l1与y轴交于点E,与直线CB交于点D,过点E作y轴的垂线l2,若点P为y轴上一个动点,Q为直线l2上一个动点,求PD+PQ+DQ的最小值;
(3)若点M为直线AB上的一点,在y轴上是否存在点N,使以点A、D、M、N为顶点的四边形为平行四边形,若存在,请直接写出点N的坐标;若不存在,请说明理由.
【答案】(1)y=2x+4
(2)
(3)存在以点A、D、M、N为顶点的四边形为平行四边形,N的坐标为(0,﹣2)或(0,10)
【分析】(1)设OB=OC=m,由S△ABC=12,可得B(0,4),设直线AB解析式为y=kx+b,利用待定系数法即可求解;
(2)将直线AB向下平移6个单位,则直线l1解析式为y=2x−2,可得E(0,−2),垂线l2的解析式为y=−2,由B(0,4),C(4,0),得直线BC解析式为y=−x+4,从而可求得D(2,2),作D关于y轴的对称点D,作D关于直线y=−2对称点D,连接DD交y轴于P,交直线y=−2于Q,此时PD+PQ+DQ的最小,根据D(−2,2),D(2,−6),得直线DD解析式为y=−2x−2,从而P(0,−2),Q(0,−2),故此时PD=2,PQ=0,DQ=,PD+PQ+DQ的最小值为4.
(3)设P(p,2p+4),N(0,q),而A(−2,0),D(2,2),①以AD、MN为对角线,此时AD中点即为MN中点,根据中点公式得N(0,−2);②以AM、DN为对角线,同理可得N(0,10);③以AN、DM为对角线,同理可得N(0,−2).
【解析】(1)解:(1)设OB=OC=m,
∵OA=2,
∴AC=m+2,A(﹣2,0),
∵S△ABC=12,
∴AC•OB=12,即m•(m+2)=12,
解得m=4或m=﹣6(舍去),
∴OB=OC=4,
∴B(0,4),
设直线AB解析式为y=kx+b,
∴,
解得,
∴直线AB解析式为y=2x+4;
(2)将直线ABy=2x+4向下平移6个单位,则直线l1解析式为y=2x﹣2,
令x=0得y=﹣2,
∴E(0,﹣2),垂线l2的解析式为y=﹣2,
∵B(0,4),C(4,0),
设直线BC解析式为y=px+q,
∴,
解得,
∴直线BC解析式为y=﹣x+4,
由得:,
∴D(2,2),
作D关于y轴的对称点D',作D关于直线y=﹣2对称点D'',连接D'D''交y轴于P,交直线y=﹣2于Q,此时PD+PQ+DQ的最小,如图:
∴D'(﹣2,2),D''(2,﹣6),
设直线D'D''解析式为y=sx+t,
则,解得,
∴直线D'D'解析式为y=﹣2x﹣2,
令x=0得y=﹣2,即P(0,﹣2),
令y=﹣2得x=0,即Q(0,﹣2),
∴此时PD=2,PQ=0,DQ=2,
∴PD+PQ+DQ的最小值为4.
(3)存在,理由如下:
设P(p,2p+4),N(0,q),而A(﹣2,0),D(2,2),
①以AD、MN为对角线,如图:
此时AD中点即为MN中点,
∴,解得,
∴N(0,﹣2);
②以AM、DN为对角线,如图:
同理可得:,解得,
∴N(0,10);
③以AN、DM为对角线,如图:
同理可得,解得,
∴N(0,﹣2),
综上所述,以点A、D、M、N为顶点的四边形为平行四边形,N的坐标为(0,﹣2)或(0,10).
一、单选题
1.如图,点M是菱形ABCD的边BC的中点,P为对角线BD上的动点,若AB=2,∠A=120°,则PM+PC的最小值为( )
A.2B.C.D.1
【答案】B
【分析】连接AM、AC,AM交BD于P,此时PM+PC最小,连接CP,由菱形的性质可知C和A关于BD对称,AP=CP,由条件易证△ABC是等边三角形,根据三线合一可知AM⊥BC,再根据勾股定理可求AM的值,即可求解.
【解析】解:连接AM、AC,AM交BD于P,
此时PM+PC最小,连接CP,
∵四边形ABCD是菱形,
∴OA=OC,AC⊥BD,
∴C和A关于BD对称,
∴AP=PC,
∵∠A=120°,
∴∠ABC=60°,
∴△ABC是等边三角形,
∴AC=AB=2,
∵M是BC的中点,
∴AM⊥BC,
∴∠BAM=30°,
∴BM=1,
∴AM=,
∴PM+PC=AM=.
故选B.
2.已知线段AB及直线l,在直线上确定一点,使最小,则下图中哪一种作图方法满足条件( ).
A.B.
C.D.
【答案】C
【分析】根据对称的性质以及两点之间线段最短即可解决问题.
【解析】解:∵点A,B在直线l的同侧,
∴作B点关于l的对称点B',连接AB'与l的交点为P,由对称性可知BP=B'P,
∴PA+PB=PB′+PA=AB′为最小
故选:C.
3.如图1,在菱形ABCD中,AB=6,∠BAD=120°,点E是BC边上的一动点,点P是对角线BD上一动点,设PD的长度为x,PE与PC的长度和为y,图2是y关于x的函数图象,其中H(a,b)是图象上的最低点,则a+b的值为( )
A.B.C.D.36
【答案】A
【分析】从图2知,是的最小值,从图1作辅助线知;接下来求出,设与交于点,则求出,,最后得,所以,选.
【解析】解:如下图,在边上取点,使得和关于对称,
连接,得,
连接,作,垂足为,
由三角形三边关系和垂线段最短知,
,
即有最小值,
菱形中,,,
在△中,,
解得,
是图象上的最低点
,
此时令与交于点,
由于,在△中,
,又,
,
又的长度为,图2中是图象上的最低点,
,
又,
,
故选:A.
4.如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是边AC上一点,若AE=2,则EM+CM的最小值为( )
A.B.3C.2D.4
【答案】C
【分析】连接BE,交AD于点M,过点E作EF⊥BC交于点F,此时EM+CM的值最小,求出BE即可.
【解析】解:连接BE,交AD于点M,过点E作EF⊥BC交于点F,
∵△ABC是等边三角形,AD是BC边上的中线,
∴B点与C点关于AD对称,
∴BM=CM,
∴EM+CM=EM+BM=BE,此时EM+CM的值最小,
∵AC=6,AE=2,
∴EC=4,
在Rt△EFC中,∠ECF=60°,
∴FC=2,EF=2,
在Rt△BEF中,BF=4,
∴BE=2,
故选:C.
5.如图,正方形ABCD的边长是4,点E是DC上一个点,且DE=1,P点在AC上移动,则PE+PD的最小值是( )
A.4B.4.5C.5.5D.5
【答案】D
【分析】连接BE,交AC于点N',连接DN',N'即为所求的点,则BE的长即为DP+PE的最小值,利用勾股定理求出BE的长即可.
【解析】解:如图,
∵四边形ABCD是正方形,
∴点B与点D关于直线AC对称,
连接BE,交AC于点N',连接DN',
∴DN'=BN',
DN'+EN'=BN'+ EN'BD,
则BE的长即为DP+PE的最小值,
∴AC是线段BD的垂直平分线,
又∵CE=CD-DE=4-1=3,
在Rt△BCE中,
BE2=CE2+BC2=25,
∵BE>0,
∴BE=5,
即DP+PE的最小值为5,
故选:D.
6.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是( )
A.1.5B.1.2C.2.4D.以上都不对
【答案】B
【解析】思路引领:先依据勾股定理求得AB的长,然后依据翻折的性质可知PF=FC,故此点P在以F为圆心,以2为半径的圆上,依据垂线段最短可知当FP⊥AB时,点P到AB的距离最短,然后依据题意画出图形,最后,利用相似三角形的性质求解即可.
答案详解:如图所示:当PE∥AB.
在Rt△ABC中,∵∠C=90°,AC=6,BC=8,
∴AB10,
由翻折的性质可知:PF=FC=2,∠FPE=∠C=90°.
∵PE∥AB,
∴∠PDB=90°.
由垂线段最短可知此时FD有最小值.
又∵FP为定值,
∴PD有最小值.
又∵∠A=∠A,∠ACB=∠ADF,
∴△AFD∽△ABC.
∴,即,解得:DF=3.2.
∴PD=DF﹣FP=3.2﹣2=1.2.
故选:B.
7.如图,矩形中,,点是矩形内一动点,且,则的最小值是( )
A.B.
C.D.
【答案】B
【分析】作PM⊥AD于M,作点D关于直线PM的对称点E,连接PE,EC.设AM=x.由PM垂直平分线段DE,推出PD=PE,推出PC+PD=PC+PE≥EC,利用勾股定理求出EC的值即可.
【解析】解:如图,作PM⊥AD于M,作点D关于直线PM的对称点E,连接PE,EC.设AM=x.
∵四边形ABC都是矩形,
∴AB∥CD,AB=CD=4,BC=AD=6,
∵S△PAB=S△PCD,
∴×4×x=××4×(6-x),
∴x=2,
∴AM=2,DM=EM=4,
在Rt△ECD中,EC==4,
∵PM垂直平分线段DE,
∴PD=PE,
∴PC+PD=PC+PE≥EC,
∴PD+PC≥4,
∴PD+PC的最小值为4.
故选:B.
8.如图,在△ABC中,AB=2,∠ABC=60°,∠ACB=45°,D是BC的中点,直线l经过点D,AE⊥l,BF⊥l,垂足分别为E,F,则AE+BF的最大值为( )
A.B.2C.2D.3
【答案】A
【分析】把要求的最大值的两条线段经过平移后形成一条线段,然后再根据垂线段最短来进行计算即可.
【解析】解:如图,过点C作CK⊥l于点K,过点A作AH⊥BC于点H,
在Rt△AHB中,
∵∠ABC=60°,AB=2,
∴BH=1,AH=,
在Rt△AHC中,∠ACB=45°,
∴AC=,
∵点D为BC中点,
∴BD=CD,
在△BFD与△CKD中,
,
∴△BFD≌△CKD(AAS),
∴BF=CK,
延长AE,过点C作CN⊥AE于点N,
可得AE+BF=AE+CK=AE+EN=AN,
在Rt△ACN中,AN<AC,
当直线l⊥AC时,最大值为,
综上所述,AE+BF的最大值为.
故选:A.
二、填空题
9.在现实生活中,我们经常会看到许多“标准”的矩形,如我们的课本封面、A4的打印纸等,其实这些矩形的长与宽之比都为,我们不妨就把这样的矩形称为“标准矩形”,在“标准矩形”中,如图所示,点在上,且,若为边上一动点,当的周长最小时,则的值为______.
【答案】
【分析】先设出矩形的边长,将AQ和CQ表示出来,再通过作对称点确定△AGQ的周长最小时的G点位置后,利用平行线分线段成比例的基本事实的推论建立等式求解即可.
【解析】解:设DC=,DQ=AD=x,
∴
∵矩形ABCD,
∴∠D=∠DCB=∠B=90°,,
∴,
如图,作Q点关于BC的对称点E,连接AE交BC于点M,
∴GQ=GE,CQ=CE=
∴AQ+QG+AG=,
∴当A、G、E三点共线时,△AGQ的周长最小,
此时G点应位于图中的M点处;
∵矩形ABCD中,∠QCG=90°,
∴E点位于QC的延长线上,
∴CE∥AB,
∴,
即,
故答案为:.
10.如图,点是内任意一点,,点和点分别是射线和射线上的动点,,则周长的最小值是______.
【答案】3
【分析】根据“将军饮马”模型将最短路径问题转化为所学知识“两点之间线段最短”可找到周长的最小的位置,作出图示,充分利用对称性以及,对线段长度进行等量转化即可.
【解析】
解:如图所示,过点P分别作P点关于OB、OA边的对称点、,连接、、、、,其中分别交OB、OA于点N、M,根据“两点之间线段最短”可知,此时点M、N的位置是使得周长的最小的位置.
由对称性可知:,
,
为等边三角形
的周长===3
故答案为:3
11.如图,菱形ABCD 的边长为6,∠ABC=120°,M是BC边的一个三等分点,P是对角线AC上的动点,当 PB+PM 的值最小时,PM的长是________.
【答案】
【分析】如图,连接DP,BD,作DH⊥BC于H.当D、P、M共线时, 值最小,利用勾股定理求出DM,再利用平行线的性质即可解决问题.
【解析】解:如图,连接DP,BD,作DH⊥BC于H.
∵四边形ABCD是菱形,
∴AC⊥BD,B、D关于AC对称,
∴PB+PM=PD+PM
当D、P、M共线时,的值最小,
∵CM=BC=2
∵∠ABC=120°,
∴∠DBC=∠ABD=60°
∴△DBC是等边三角形,
∵BC=6,
∴CM=2,HM=1,DH= ,
在Rt△DMH中,
∵CM∥AD
∴
∴
故答案为:.
12.如图,等边的边长为4,点是边的中点,点是的中线上的动点,则的最小值是_____.
【答案】
【分析】当连接BE,交AD于点P时,EP+CP=EP+PB=EB取得最小值.
【解析】解:连接BE
∵△ABC是等边三角形,AD是BC边上的中线,
∴AD⊥BC,
∴AD是BC的垂直平分线,
∴点C关于AD的对应点为点B,
∴BE就是EP+CP的最小值.
∵△ABC是等边三角形,E是AC边的中点,
∴BE是△ABC的中线,
∴CE=AC=2,
∴
即EP+CP的最小值为,
故答案为:.
13.如图,等边三角形的边上的高为6,是边上的中线,M是线段上的-一个动点,E是中点,则的最小值为_________.
【答案】6
【分析】连接BE交AD于M,则BE就是EM+CM的最小值,通过等腰三角形的“三线合一”,可得BE=AD即可得出结论.
【解析】解:连接BE,与AD交于点M.
∵AB=AC,AD是BC边上的中线,
∴B、C关于AD对称,则EM+CM=EM+BM,
则BE就是EM+CM的最小值.
∵E是等边△ABC的边AC的中点,AD是中线
∴BE=AD=6,
∴EM+CM的最小值为6,
故答案为:6.
14.如图,正方形ABCD的边长为8,点M在DC上且DM=2,N是AC上的一动点,则DN+MN的最小值是______.
【答案】10
【分析】要求DN+MN的最小值,DN,MN不能直接求,可考虑通过作辅助线转化DN,MN的值,从而找出其最小值求解.
【解析】解:∵正方形是轴对称图形,点B与点D是关于直线AC为对称轴的对称点,
∴连接BN,BD,
∴BN=ND,
∴DN+MN=BN+MN,
连接BM交AC于点P,
∵点 N为AC上的动点,
由三角形两边和大于第三边,
知当点N运动到点P时,BN+MN=BP+PM=BM,
BN+MN的最小值为BM的长度,
∵四边形ABCD为正方形,
∴BC=CD=8,CM=8﹣2=6,∠BCM=90°,
∴BM==10,
∴DN+MN的最小值是10.
故答案为:10.
三、解答题
15.如图,在一条东西向的马路上有广场A和医院C,在各自正北方向上分别有汽车站B和汽车站D,已知AC=14km,AB=4km,CD=8km,市政府打算在马路AC段之间建造一个加油站P.
(1)若要使得加油站P到两汽车站的距离之和最小,请用尺规作图在图1中作出加油站P的位置,并直接写出此时的最小值.(作图请保留痕迹,结果可以保留根号)
(2)若要使得加油站到两汽车站的距离相等,请用尺规作图在图2中作出加油站P的位置,并求出此时PA的距离.(作图请保留痕迹)
【答案】(1)图见解析,km;(2)图见解析,km.
【分析】(1)作点B关于AC的对称点B′,连接DB′交AC于点P,连接PB,此时PB+PD的值最小,利用勾股定理求出最小值;
(2)连接BD,作线段BD的垂直平分线交AC于点P,连接PB,PD,点P即为所求,设PA=xkm,利用勾股定理求解即可.
【解析】解:(1)如图1中,点P即为所求.
过点D作DE⊥AB交AB的延长线于点E.则四边形ACDE是矩形,
∴AC=DE=14(km),CD=AE=8(km),
∵AB=AB′=4km,
∴EB′=AE+AB′=12(km),
∴PB+PD的最小值=DB′===(km).
(2)如图2中,点P即为所求,
设PA=xkm,CP=(14﹣x)km,
∵∠A=∠C=90°,
在Rt△ABP和Rt△PCD中,PB=PD,
∴42+x2=82+(14﹣x)2,
解得x=
∴AP=(km).
16.如图,一个牧童在小河的南4华里(长度单位)的A处牧马,而他正位于他的小屋B的西8华里北7华里处,他想把他的马牵到小河边去饮水,然后回家,他要完成这件事情所走的最短路程是多少?
【答案】17华里
【分析】作出A点关于MN的对称点,连接交MN于点P,则就是最短路线,根据垂直平分线的性质,得出,根据勾股定理得出,即可求出最短路径.
【解析】解:作出A点关于MN的对称点,连接交MN于点P,则就是最短路线,如图所示:
,,,
∵MN垂直平分,
∴,
∵在中,,
∴,
∴(华里).
答:牧童所走的最短里程是17华里.
17.如图,在平面直角坐标系中,已知点,,.
(1)画出关于轴对称的;
(2)在轴上找一点,使的值最小(保留作图痕迹),并写出点的坐标.
【答案】(1)见解析;
(2)见解析,的坐标为.
【分析】(1)根据轴对称的性质结合坐标系,分别确定点A、B、C关于y轴的对称点A1、B1、C1,即可作出;
(2)作出点B关于x轴的对称点B2,连接B2C,交x轴于P,点P即为所求做的点.
【解析】(1)解:解:(1)如图所示,即为关于轴对称的三角形.
(2)解:如图所示,点P即为所求做的点,点的坐标为.
18.如图,方格图中每个小正方形的边长为1,点A,B,C都是格点.
(1)画出△ABC关于直线MN对称的.
(2)若B为坐标原点,请写出、、的坐标,并直接写出的长度..
(3)如图2,A,C是直线同侧固定的点,D是直线MN上的一个动点,在直线MN上画出点D,使最小.(保留作图痕迹)
【答案】(1)画图见解析;(2),;(3)画图见解析
【分析】(1)分别确定关于对称的对称点 再顺次连接从而可得答案;
(2)根据在坐标系内的位置直接写其坐标与的长度即可;
(3)先确定关于的对称点,再连接 交于 则 从而可得答案.
【解析】解:(1)如图1,是所求作的三角形,
(2)如图1,为坐标原点,
则
(3)如图2,点即为所求作的点.
19.如图,一次函数y=kx﹣6过点A(﹣2,﹣2),与y轴交于点B.
(1)求一次函数表达式及点B坐标;
(2)在x轴上找一点C,连接BC,AC.当BC+AC最小时,
①请直接写出点C的坐标为______;
②请直接写出直线BC的函数表达式为______;
③在坐标轴上找点D,连接BD,CD,使S△ABC=S△BCD,请直接写出点D的坐标为_____.
【答案】(1)y=-2x-6,B(0,-6)
(2)①(-,0);②y=-4x-6;③或或(0,-2)或(0,-10)
【分析】(1)利用待定系数法即可求得一次函数的解式,进入求得B的坐标;
(2)①作B关于x轴的对称点为(0,6),连,交x轴于点C,此时BC+AC最小,用待定系数法求出,进一步求出C点坐标;②利用待定系数法即可求得直线BC的解析式;③求得△ABC的面积,然后根据三角形面积公式得CD和BD的长度进而即可求得D的坐标.
【解析】(1)解:∵一次函数y=kx﹣6过点A(﹣2,﹣2)
∴-2=-2k-6,解得k=-2
∴y=-2x-6
∴B(0,-6)
(2)①B点关于x轴的对称点是,连接交x轴于点C,此时AC+BC最小,
设直线的解析式为y=ax+b,则
解得
∴y=4x+6
∴当y=0时,x=-,
∴点C(-,0)
故答案为:(-,0)
②设直线BC的解析式为y=mx+n,则
,
解得
∴y=-4x-6
故答案为:y=-4x-6
③∵A(-2,-2),B(0,-6) ,C
∴
当D在x轴时, ,
即
∴CD=1
∴点D为 或
当D在y轴上时,
即
∴BD=4
∴点D为(0,-2)或(0,-10)
故答案为: 或或(0,-2)或(0,-10)
20.教材呈现:下图是华师版八年级下册数学教材第111页的部分内容.
(1)问题解决:请结合图①,写出例1的完整解答过程.
(2)问题探究:在菱形ABCD中,对角线AC、BD相交于点O,AB=4,∠BAD=2∠ABC.过点D作DE//AC交BC的延长线于点E.如图②,连结OE,则OE的长为____.
(3)如图③,若点P是对角线BD上的一个动点,连结PC、PE,则PC+PE的最小值为_____.
【答案】(1)见解析;(2);(3)
【分析】(1)根据菱形的性质先得出,进而证明是等边三角形.
(2)先证明四边形ACED是菱形,再求出,用勾股定理即可求出OE的长.
(3)先找出点A的对称点,根据对称性得到PC+PE的最小值为AE的长,利用勾股定理求出AE的长即可.
【解析】(1)四边形ABCD是菱形,
∴AD//BC,
.
,
.
四边形ABCD是菱形,
.
是等边三角形.
(2)四边形ABCD是菱形,
∴AD//BC,
又∵DE//AC,
四边形ACED是平行四边形,
由(1)可得,
故四边形ACED是菱形;
则,,∠BDC=30°,OA=2,
则.
(3)如图所示,过A作BE的垂线交BE于点F,连接AE,
A点关于BD的对称点为点C,
则PC+PE的最小值为AE;
为等边三角形,
,
,,
则PC+PE的最小值为.
21.如图,直线经过、两点,直线与直线交于点C,与x轴交于点D.
(1)求点C的坐标;
(2)点P是y轴上一点,当四边形PDCB的周长最小时,求四边形PDCB的面积;
(3)把直线沿y轴向上平移9个单位长度,得到新直线与直线交于点E,试探究在x轴上是否存在点Q,在平面内存在点F使得以点D,Q,E,F为顶点的四边形是菱形(含正方形)?若存在,直接写出符合条件的点Q的坐标;若不存在,说明理由.
【答案】(1)点C的坐标为
(2)
(3)存在,点Q的坐标为:,,,
【分析】(1)由待定系数法求出直线的解析式为,然后联立直线与直线,即可求出点C的坐标;
(2)如图,作点D关于y轴的对称点,连接交y轴于点P,连接DP,当、、三点共线时,四边形PDCB的周长最小,求出直线的解析式为,则可求,进而由求解即可;
(3)由题意可知直线的解析式为,联立线与直线,求出,设,分三种情况,①当ED为菱形对角线时,利用可得点Q坐标;②当EQ为菱形对角线时,利用可得点Q坐标;③当EF为菱形对角线时,利用可得点Q坐标.
【解析】(1)解:设直线的解析式为,由直线经过、两点可得:
,解得,
直线的解析式为,
又直线与直线交于点C,
,解得,
当时,则,
点C的坐标为;
(2)解:如图,作点D关于y轴的对称点,连接交y轴于点P,连接DP,根据两点之间“线段最短”可知,当、、三点共线时,四边形PDCB的周长最小,
直线与x轴的交点为,
又点D和点关于y轴对称,
点,
,
设直线的解析式为,可得,解得,
直线的解析式为,
令,则,得点,
,
又,,
,
,
;
(3)解:由题意可得直线的解析式为,
联立线与直线,即,解得,,
设,
①当ED为菱形对角线时,,
即,
解得,
;
②当EQ为菱形对角线时,,
,
,
解得或,
,;
③当EF为菱形对角线时,,
即,
解得,
,
综上:存在,点Q的坐标为:,,,.
22.如果有一条直线经过三角形的某个顶点,将三角形分成两个三角形,其中一个三角形与原三角形相似,则称该直线为三角形的“自相似分割线”.如图1,在△ABC中,AB=AC=1,∠BAC=108°,DE垂直平分AB,且交BC于点D,连接AD.
(1)证明直线AD是△ABC的自相似分割线;
(2)如图2,点P为直线DE上一点,当点P运动到什么位置时,PA+PC的值最小?求此时PA+PC的长度.
(3)如图3,射线CF平分∠ACB,点Q为射线CF上一点,当取最小值时,求∠QAC的正弦值.
【答案】(1)直线AD是△ABC的自相似分割线;
(2)当点运动到点时,PA+PC的值最小,此时;
(3)∠QAC的正弦值为
【分析】(1)根据定义证明△DBA∽△ABC即可得证;
(2)根据垂直平分线的性质可得,当点与重合时,,此时最小,设,则
根据,列出方程,解方程求解即可求得,进而即可求得的长,即最小值;
(3)过点作于点,过点作于点,连接,设与交于点,根据已知条件求得,进而转化为,则当点落在上时,点与点重合,此时的值最小,最小值为,进而根据求解即可.
【解析】(1)∵△ABC中,AB=AC=1,∠BAC = 108°
∴∠B =∠C =(180°-∠BAC)= 36°
∵DE垂直平分AB
∴AD = BD
∴∠B =∠BAD = 36°
∴∠C =∠BAD
又∵∠B =∠B
∴△DBA∽△ABC
∴直线AD是△ABC的自相似分割线.
(2)如图,连接,,
垂直平分AB,
当点与重合时,,此时最小,
,
设,则
解得:
PA+PC=
当点运动到点时,PA+PC的值最小,此时;
(3)如图,过点作于点,过点作于点,连接,设与交于点,
,
由(2)知,
平分
点落在上时,点与点重合,
即此时的值最小,最小值为
∠QAC的正弦值为
专题24 最值模型之将军饮马模型-备战2024年中考数学常见模型题型归纳与总结高分突破(全国通用): 这是一份专题24 最值模型之将军饮马模型-备战2024年中考数学常见模型题型归纳与总结高分突破(全国通用),文件包含专题24最值模型之将军饮马模型原卷版docx、专题24最值模型之将军饮马模型解析版docx等2份试卷配套教学资源,其中试卷共69页, 欢迎下载使用。
专题32 几何变换之旋转模型 2024年中考数学核心几何模型重点突破(全国通用): 这是一份专题32 几何变换之旋转模型 2024年中考数学核心几何模型重点突破(全国通用),文件包含专题32几何变换之旋转模型答案详解docx、专题32几何变换之旋转模型docx等2份试卷配套教学资源,其中试卷共55页, 欢迎下载使用。
专题30 几何变换之平移模型 2024年中考数学核心几何模型重点突破(全国通用): 这是一份专题30 几何变换之平移模型 2024年中考数学核心几何模型重点突破(全国通用),文件包含专题30几何变换之平移模型答案详解docx、专题30几何变换之平移模型docx等2份试卷配套教学资源,其中试卷共55页, 欢迎下载使用。












