江西省丰城中学2022-2023学年高一上学期期末考试数学试题

这是一份江西省丰城中学2022-2023学年高一上学期期末考试数学试题，共9页。试卷主要包含了已知全集，集合，则，若正实数满足，则等内容，欢迎下载使用。

考试时间：2023年1月11日15：50-17：50 总分：150分；时长：120分钟
一､单选题：（本大题共8小题，每小题5分，满分40分.在每小题给出的四个选项中，只有一项是符合题目要求的）
1.已知全集，集合，则（ ）
A. B. C. D.
2.已知实数满足，则下列不等式一定成立的是（ ）
A. B.
C. D.
3.若“”为真命题，则实数的最小值为（ ）
A. B. C.6 D.7
4.已知定义域为的函数不是偶函数，则下列命题一定为真命题的是（ ）
A.
B.
C.
D.
5.某商场开通三种平台销售商品，五一期间这三种平台的数据如图1所示.该商场为了解消费者对各平台销售方式的满意程度，用分层抽样的方法抽取了的顾客进行满意度调查，得到的数据如图2所示.下列说法正确的是（ ）
A.总体中对平台一满意的消费人数约为36
B.样本中对平台二满意的消费人数为300
C.样本中对平台一和平台二满意的消费总人数为54
D.若样本中对平台三满意的消费人数为120，则
6.用二分法求函数的一个正零点的近似值（精确度为）时，依次计算得到如下数据：，关于下一步的说法正确的是（ ）
A.已经达到精确度的要求，可以取作为近似值
B.已经达到精确度的要求，可以取作为近似值
C.没有达到精确度的要求，应该接着计算
D.没有达到精确度的要求，应该接着计算
7.若正实数满足，则.（ ）
A.有最大值4 B.有最小值
C.有最大值 D.有最小值
8.设，函数在区间上的最小值为，则的取值范围为（ ）.
A.或 B.或
C.或 D.前面三个答案都不对
二､多选题：（本大题共4小题，每小题5分，满分20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.）
9.若方程在区间上有实数根，则实数的取值可以是（ ）
A. B. C. D.1
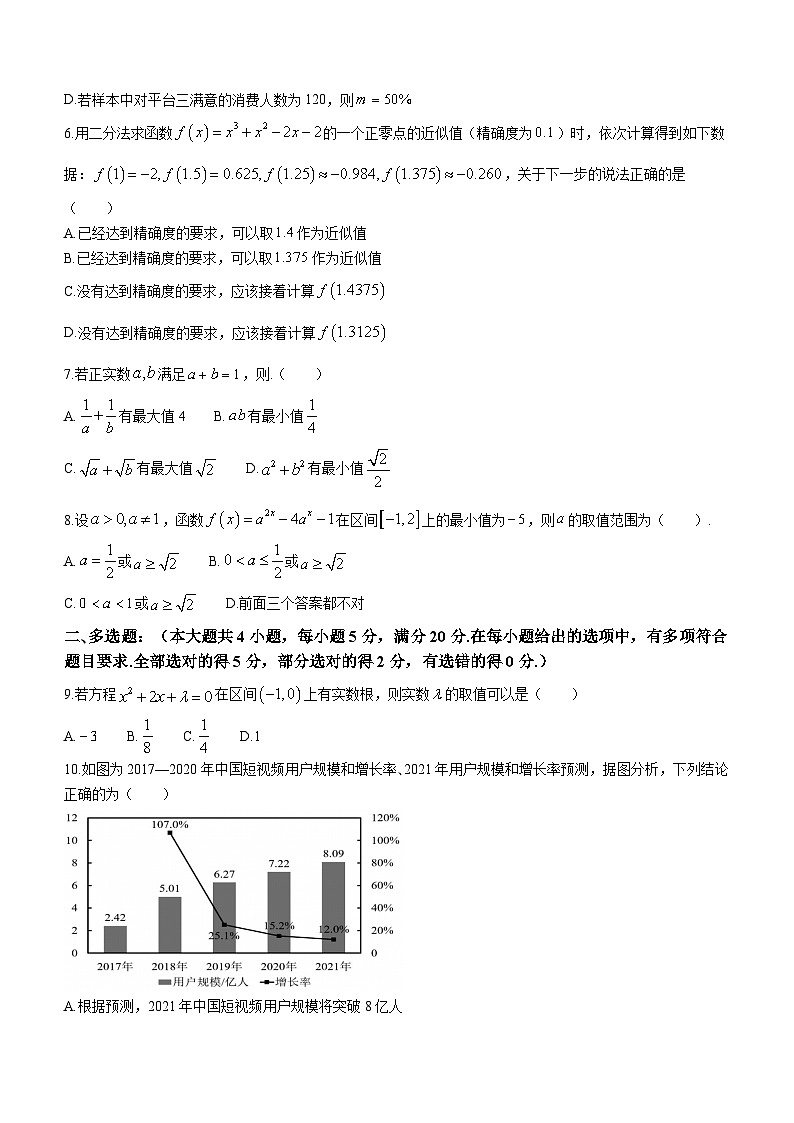
10.如图为2017—2020年中国短视频用户规模和增长率､2021年用户规模和增长率预测，据图分析，下列结论正确的为（ ）
A.根据预测，2021年中国短视频用户规模将突破8亿人
B.2017—2020年中国短视频用户规模逐年增加，但增长速度变缓
C.2018年中国短视频用户规模比2017年增加了超过两倍
D.2020年中国短视频用户规模与2017年相比较，增长率约为
11.已知函数是定义在上的奇函数，则下列结论正确的是（ ）
A.
B.若在上为增函数，则在上为减函数
C.若在上有最小值，则在上有最大值1
D.若时，，则时，
12.关于函数，下列描述正确的有（ ）
A.函数在区间上单调递增
B.函数的图象关于直线对称
C.函数有且仅有两个零点
D.若，但，则
三､填空题：（本大题共4小题，每小题5分，满分20分）
13.已知幂函数的图象过点，则__________.
14.__________.
15.若函数则__________.
16.已知函数有且只有一个零点，若方程无解，则实数的取值范围为__________.
四､解答题：（本大题共6小题，满分70分，解答须写出文字说明､证明过程和演算步骤）
17.（满分10分）已知集合或.
（1）若，求
（2）若，求实数的取值范围.
18.（满分12分）目前，“新冠肺炎”在我国得到了很好的遏制，但在世界其他一些国家还大肆流行.因防疫需要，某学校决定对教室采用药熏消毒法进行消毒，药熏开始前要求学生全部离开教室.已知在药熏过程中，教室内每立方米空气中的药物含量（毫克）与药熏时间（小时）成正比；当药熏过程结束，药物即释放完毕，教室内每立方米空气中的药物含量（毫克）达到最大值.此后，教室内每立方米空气中的药物含量（毫克）与时间（小时）的函数关系式为（为常数）.已知从药熏开始，教室内每立方米空气中的药物含量（毫克）关于时间（小时）的变化曲线如图所示.
（1）从药熏开始，求每立方米空气中的药物含量（毫克）与时间（小时）之间的函数关系式；
（2）据测定，当空气中每立方米的药物含量不高于毫克时，学生方可进入教室，那么从药熏开始，至少需要经过多少小时后，学生才能回到教室？
19.（满分12分）设函数.
（1）若不等式的解集为，求实数的值；
（2）若，且存在，使成立，求实数的取值范围.
20.（满分12分）某区政府组织了以“不忘初心，牢记使命”为主题的教育活动，为统计全区党员干部一周参与主题教育活动的时间，从全区的党员干部中随机抽取名，获得了他们一周参与主题教育活动时间（单位：）的频率分布直方图如图所示，已知参与主题教育活动时间在内的人数为92.
（1）求的值.
（2）以每组数据所在区间的中点值作为本组的代表，估算这些党员干部参与主题教育活动时间的平均值以及中位数（中位数精确到）.
（3）如果计划对参与主题教育活动时间在内的党员干部给予奖励，且在内的分别评为二等奖和一等奖，那么按照分层抽样的方法从获得一､二等奖的党员干部中选取5人参加社区义务宣讲活动，再从这5人中随机抽取2人作为主宣讲人，求这2人均是二等奖的概率.
21.（满分12分）已知函数满足对任意，都有恒成立.且当时，.
（1）求，判断在上的单调性，并证你的结论：
（2）解不等式.
22.（满分12分）设函数是定义域为的奇函数.
（1）求；
（2）若，求使不等式对一切恒成立的实数的取值范围；
（3）若函数的图象过点，是否存在正数，使函数在上的最大值为2，若存在，求出的值；若不存在，请说明理由.
丰城中学2022-2023学年上学期高一期末考试
数学答案
13. 14. 15.13 16.
17.（满分10分）（1）见解析（2）
【详解】（1）若，则，
所以或
（2）若，则集合为集合的子集，当时，即，解得；
当时，即，解得，又或，由，
则或，解得或.
综上所述：实数的取值范围为
18.（满分12分）（1）；（2）小时.
（1）依题意，当时，可设，且，解得，又由，
解得，所以
（2）令，即，得，解得，
即至少需要经过后，学生才能回到教室.
19.（满分12分）（1）；（2）或
（1）解：因为的解集为，所以
解得；
（2）因为，所以，因为存在，
成立，即存在成立，当时，，成立；当时，
函数图象开口向下，成立；当时，，
即，解得或，此时，或，
综上：实数的取值范围或.
20.（满分12分）（1）由已知可得.
则，得
（2）这些党员干部参与主题教育活动时间的平均值为：
设中位数为，则，得
（3）按照分层抽样的方法从内选取的人数为，从内选取的人数为.
记二等奖的4人分别为，一等奖的1人为，
事件为“从这5人中抽取2人作为主宣讲人，且这2人均是二等奖”.
从这5人中随机抽取2人的基本事件为，，共10种，
其中2人均是二等奖的情况有，共6种，
由古典概型的概率计算公式得.
21.（满分12分）（1）对任意，都有，令，可得，又；
函数在上递减.设，则，则且
，
则函数在上单调递减；
（2）由（1）可知，，
又对任意，都有，
根据函数在上单调递减可得，，故不等式的解集为
22.（满分12分）（1）（2）（3）
（1）解：函数是定义域为的奇函数，
所以，解得，此时，
满足
（2）因为，所以，解得，所以
在上是减函数，等价于
，所以，即，
又因为不等式对一切恒成立，所以
对一切恒成立，所以，解得，
所以实数的取值范围是；
（3）因为函数的图象过点，所以，解得，
则，令，
则，当时，是减函数，，
因为函数在上的最大值为2，所以，即，
解得，不成立；当时，是增函数，
因为函数在上的最大值为2，所以，
解得或（舍去），所以存在正数，
使函数在上的最大值为2.题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
D
B
C
C
C
C
B
BC
ABD
ACD
ABC