2022-2023学年广东省汕头市金平区五年级（下）期末数学试卷

这是一份2022-2023学年广东省汕头市金平区五年级（下）期末数学试卷，共14页。试卷主要包含了仔细推敲，我会辨，比较斟酌，我会选，用心思考，我会填，仔细观察，我会算，动手操作，我会画，解决问题，我能行等内容，欢迎下载使用。

1．因为，所以这两个分数的分数单位相同。
2．一个棱长总和是12cm的正方体，它的体积就是1cm3。
3．任意奇数加上1后，所得的结果一定是2的倍数。
4．在钟面上，从6：00到9：00，时针旋转了30°。
5．要反映汕头市今年春季的降水量变化情况可以选用折线统计图。
二、比较斟酌，我会选。（请将答题卡上对应的选项涂黑。）
6．a+3的和是奇数，a一定是（ ）
A．奇数B．偶数C．合数
7．三位同学合作折千纸鹤。甲完成了总量的，乙完成了总量的，丙完成了总量的，他们完成计划总量的情况是（ ）
A．还未完成B．正好完成C．超额完成
8．如图绕O点按顺时针方向旋转90°后得到的图形是​（ ）
A．B．C．
9．一个长方体纸盒，长8cm，宽6cm，高5cm，最多可以完整放入（ ）块棱长2cm的正方体积木。
A．24B．30C．120
10．用5个小立方体摆成从上面看到的图形和从上面看时一样的立体图形，有（ ）种摆法。
A．4种B．3种C．2种
三、用心思考，我会填。（请将答案直接写在答题卡指定的位置上。）
11．填上适当的分数。
900dm3＝ m3；45分钟＝ 小时。
12．1里面含有 个，再加上 个这样的分数单位就是最小的质数。
13．在自然数中，最小的奇数是 ；最小的合数是 。
14．一个正方体的棱长是它的棱长总和的 ，一个面的面积是它的表面积的 ．
15．一瓶IL的橙汁正好倒满4个相同的杯子，每杯橙汁的容量是这瓶橙汁的，每杯橙汁是 毫升。
16．分母是5的最大真分数是 ，最小假分数是 ．
17．从如图中的长方体木块切出一个最大正方体，这个正方体的表面积是 平方厘米。
18．10÷ ＝＝ ÷10＝ （填小数）。
19．如图中露出来的五角星是单位“1”的，遮住的部分是单位“1”的，一共有 个五角星。
​
20．如图中一共有 个小正方体，至少再增加 个小正方体，就可以拼成一个较大正方体。
四、仔细观察，我会算。
21．直接写得数。
22．计算下面各题，能简算的要简算。
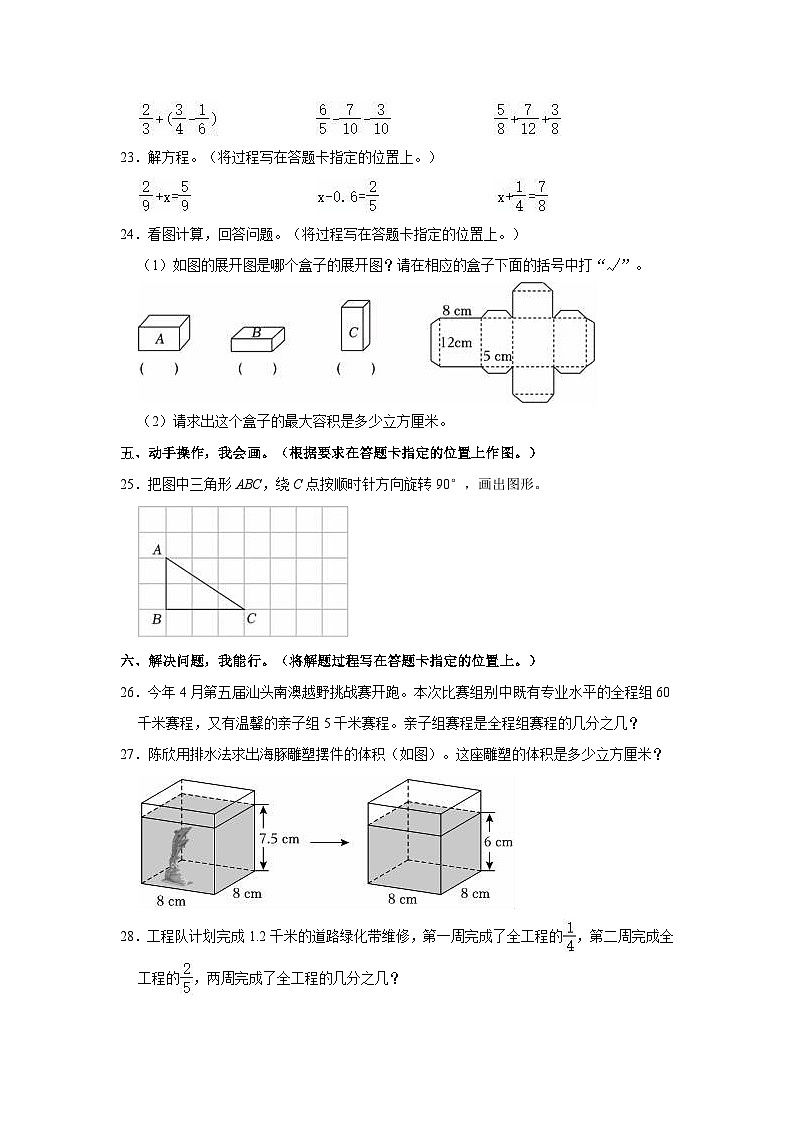
23．解方程。（将过程写在答题卡指定的位置上。）
24．看图计算，回答问题。（将过程写在答题卡指定的位置上。）
（1）如图的展开图是哪个盒子的展开图？请在相应的盒子下面的括号中打“√”。
（2）请求出这个盒子的最大容积是多少立方厘米。
五、动手操作，我会画。（根据要求在答题卡指定的位置上作图。）
25．把图中三角形ABC，绕C点按顺时针方向旋转90°，画出图形。
六、解决问题，我能行。（将解题过程写在答题卡指定的位置上。）
26．今年4月第五届汕头南澳越野挑战赛开跑。本次比赛组别中既有专业水平的全程组60千米赛程，又有温馨的亲子组5千米赛程。亲子组赛程是全程组赛程的几分之几？
27．陈欣用排水法求出海豚雕塑摆件的体积（如图）。这座雕塑的体积是多少立方厘米？
​
28．工程队计划完成1.2千米的道路绿化带维修，第一周完成了全工程的，第二周完成全工程的，两周完成了全工程的几分之几？
29．一节体育课40分钟。老师示范立定跳远动作要领用了小时，同学们进行练习用了小时，余下的时间进行体能训练，同学们进行体能训练用了多少时间？
30．根据统计图中的信息填空。
汕头的湿地资源丰富，其中红树林资源尤为珍贵。近20年来，汕头市持续推进红树林的人工造林和养护工作。如图显示的是汕头市连年来累计红树林造林面积情况：
（1）汕头在2006年的红树林累计造林面积是 公顷，到2020年累计造林达到 公顷。
（2）2006年的红树林累计造林面积是2020年累计造林面积的。
（3）从 年至 年的造林面积增长得最快。
2022-2023学年广东省汕头市金平区五年级（下）期末数学试卷
参考答案与试题解析
一、仔细推敲，我会辨。（对的打“√”，错的打“x“，请将答题卡上对应的选项涂黑。）
1．【分析】把单位“1”平均分成若干份取一份的数，叫做分数单位；分数的分子是几里面就有几个这样的分数单位。
【解答】解：的分数单位是；
的分数单位是。
因此因为，所以这两个分数的分数单位不相同。原题说法错误。
故答案为：。
【点评】本题考查了分数单位的认识。
2．【分析】根据正方体的棱长总和＝棱长×12，那么棱长＝棱长总和÷12，据此求出棱长，再根据正方体的体积公式：V＝a3，把数据代入公式求出正方体的体积，然后与1立方厘米进行比较。
【解答】解：12÷12＝1（厘米）
1×1×1＝1（立方厘米）
所以一个棱长总和是12厘米的正方体，它的体积就是1立方厘米。
因此题干中的结论是正确的。
故答案为：√。
【点评】此题主要考查正方体的棱长总和公式、体积公式的灵活运用，关键是熟记公式。
3．【分析】奇数是不能被2整除的数，个位数字为1、3、5、7、9，奇数加上1后，对应的和的个位是2、4、6、8、0，个位是2、4、6、8、0的数是2的倍数。
【解答】解：任意奇数加上1后，和一定2的倍数，原题说法正确。
故答案为：√。
【点评】此题主要考查奇数和偶数的意义，需要掌握奇数的前一个数和后一个数是偶数，偶数的前一个数和后一个数是奇数。
4．【分析】钟面上12个数字，以表芯为旋转点，表针转一圈是360°，被12个数字平均分成12份，每一份也就是两数之间夹角是30°。从6：00到9：00，时针旋转了3大格，旋转角是90°。
【解答】解：3×30°＝90°
在钟面上，从6：00到9：00，时针旋转了90°。
故原题说法错误。
故答案为：。
【点评】此题考查了钟面上的角，要牢记每一大格是30°。
5．【分析】条形统计图能很容易看出数量的多少；折线统计图不仅容易看出数量的多少，而且能反映数量的增减变化情况；扇形统计图能反映部分与整体的关系；由此根据情况选择即可。
【解答】解：根据统计图的特点可知：要反映某地区近十年降水量的变化情况，应绘制折线统计图。
所以原题说法正确。
故答案为：√。
【点评】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
二、比较斟酌，我会选。（请将答题卡上对应的选项涂黑。）
6．【分析】若a+3＝5，则a＝2，可知a是偶数；由此判断即可。
【解答】解：a+3的和是奇数，a一定是偶数。
故选：B。
【点评】此题主要使用了特殊值法，要熟练掌握。
7．【分析】把计划总量看作单位“1”，把甲完成总量的分率、乙完成总量的分率、丙完成总量的分率相加，再与1比较即可。
【解答】解： ++
＝+
＝
＞1
答：他们超额完成计划总量。
故选：C。
【点评】本题主要考查了分数加法，解题的关键是掌握异分母加法运算方法。
8．【分析】在平面内，将一个图形绕一点按某个方向转动一个角度，这样的运动叫作图形的旋转。
【解答】解：绕O点按顺时针方向旋转90°后得到的图形是。
故选：A。
【点评】本题考查了旋转的意义及应用。
9．【分析】用8除以2、6乘除以2、5除以2，再把得数相乘即可解答。
【解答】8÷2＝4（块）
6÷2＝3（块）
5÷2≈2（块）
4×3×2
＝12×2
＝24（块）
答：最多可以完整放入24块棱长2cm的正方体积木。
故选：A。
【点评】本题考查的是长方体体积，分别求出长放几块，宽放几块，高放几块是解答关键。
10．【分析】根据观察，可知的上面图形为；用5个小立方体摆成从上面看到的图形为时，可以放在上面的任意位置，所以有3种摆法。
【解答】解：用5个小立方体摆成从上面看到的图形和从上面看时一样的立体图形，有3种摆法。
故选：B。
【点评】本题是考查从不同方向观察物体和几何体，关键是培养学生的观察能力。
三、用心思考，我会填。（请将答案直接写在答题卡指定的位置上。）
11．【分析】低级单位立方分米化高级单位立方米除以进率1000。
低级单位分钟化高级单位小时除以进率60。
【解答】解：900dm3＝m3；
45分钟＝小时。
故答案为：，。
【点评】单位换算首先要弄清是由高级单位化低级单位还是由低级单位化高级单位，其次记住单位间的进率。由高级单位化低级单位乘进率，由低级单位化高级单位除以进率。结果用分数表示时，通常化成最简分数。
12．【分析】＝，里面含有11个，最小的质数是2，2＝，﹣＝，里面有3个。
【解答】解：里面含有11个，再加上3个这样的分数单位就是最小的质数。
故答案为：11，3。
【点评】此题考查了分数的意义，要求学生掌握。
13．【分析】不是2的倍数的数叫做奇数；一个数，如果除了1和它本身还有别的因数，那么这样的数叫做合数；据此解答。
【解答】解：在自然数中，最小的奇数是1；最小的合数是4。
故答案为：1；4。
【点评】掌握奇数、合数的定义是解题的关键。
14．【分析】根据正方体的特征：正方体的12条棱的长度都相等，6个面的面积都相等，所以一个正方体的棱长是它的棱长总和的，一个面的面积是它的表面积的，据此解答．
【解答】解：由分析得：一个正方体的棱长是它的棱长总和的，一个面的面积是它的表面积的，
故答案为：，．
【点评】此题考查的目的是理解掌握正方体的特征，以及正方体的棱长总和公式、表面积公式的灵活运用．
15．【分析】把这瓶橙汁的体积看作单位“1”，把它平均分成4份，每份一杯，求每杯橙汁的容量是这瓶橙汁的几分之几，用1除以4；求每杯橙汁是是多少毫升，把1升化成1000毫升，用1000毫升除以4。
【解答】解：1L＝1000mL
1÷4＝
1000÷4＝250（毫升）
答：每杯橙汁的容量是这瓶橙汁的，每杯橙汁是250毫升。
故答案为：，250。
【点评】解决此题关键是弄清求的是“分率”还是“具体的数量”，求分率：平均分的是单位“1”；求具体的数量：平均分的是具体的数量。注意：分率不能带单位名称，而具体的数量要带单位名称。
16．【分析】根据真分数的意义，分子小于分母的分数是真分数，其中分子比分母小1的真分数最大；根据假分数的意义，分子大于或等于分母的分数是假分数，其中分子、分母相等的假分数最小．
【解答】解：分母为5的最大真分数是；最小假分数是；
故答案为：，．
【点评】此题主要是考查真、假分数的意义，根据意义即可判定．
17．【分析】将一个长8厘米，宽3厘米，高5厘米的长方体截成一个最大的正方体，这个正方体的棱长等于长方体的宽，根据正方体的表面积公式：S＝6a2，把数据代入公式解答即可求出正方体的表面积。
【解答】解：表面积：6×32
＝6×9
＝54（平方厘米）
答：这个正方体的表面积是54平方厘米。
故答案为：54。
【点评】此题主要考查正方体的表面积公式的灵活运用，解题关键是确定正方体的棱长等于最短边的长度。
18．【分析】根据已知的分数，利用分数的基本性质把分数的分子和分母同时乘一个不为0的数，得到与它相等的分数，再利用分子除以分母求出小数和除法算式。
【解答】解：＝＝10÷25＝＝4÷10＝0.4
故答案为：25，4，0.4。
【点评】本题主要考查分数的基本性质，根据这一性质解答即可。
19．【分析】把这些五角星的个数看作单位“1”，把它平均分成5份，露出1份，则遮住了4份，是总个数的；求一共有多少个五角星，用1份的个数乘5。
【解答】解：如图：
2×5＝10（个）
答：遮住的部分是单位“1”的，一共有10个五角星。
故答案为：，10。
【点评】此题主要是考查分数的意义。把单位“1”平均分成若干份，用分数表示，分母是平均分成的份数，分子是要表示的份数。
20．【分析】根据正方体的体积公式V＝a3可知，拼成一个较大正方体需要3×3×3＝27（个）小正方体，现在有14个，据此解答即可。
【解答】解：3×3×3＝27（个）
27﹣14＝13（个）
答：一共有14个小正方体，至少再增加13个小正方体，就可以拼成一个较大正方体。
故答案为：14，13。
【点评】本题考查了立体图形的拼切知识，结合正方体的体积公式，解答即可。
四、仔细观察，我会算。
21．【分析】根据分数加减法法则、小数乘法法则及整数除法法则直接口算。
【解答】解：
【点评】解答本题需熟练掌握分数加减法法则、小数乘法法则及整数除法法则，加强口算能力。
22．【分析】（1）一次通分，再先算小括号里面的减法，再算小括号外面的加法。
（2）根据连减的性质，a﹣b﹣c＝a﹣（b+c）计算简便。
（3）用加法交换律和结合律计算简便。
【解答】解：（1）+（）
＝+（）
＝
＝
＝
（2）
＝﹣（）
＝
＝
（3）
＝
＝
＝
【点评】此题重点考查了学生对分数混合运算的计算能力以及运算定律的掌握与运用情况。
23．【分析】根据等式的基本性质1，方程两边同时减去即可解出x的值；
根据等式的基本性质1，方程两边同时加上0.6即可解出x的值；
根据等式的基本性质1，方程两边同时减去即可解出x的值。
【解答】解： +x＝
+x﹣＝﹣
x＝
x﹣0.6＝
x﹣0.6+0.6＝+0.6
x＝0.4+0.6
x＝1
x+＝
x+﹣＝﹣
x＝﹣
x＝
【点评】本题主要考查分数方程求解，灵活应用等式的基本性质是关键。
24．【分析】（1）从展开图可以知道，盒子的长、宽、高分别是12cm、8cm、5cm，观察B盒子可见长是高的3倍以上，与展开图不符合，C盒子上下底面接近正方形，与展开图不符合，所以只有A盒子符合；
（2）用盒子的长、宽、高相乘，就求出了这个盒子的最大容积。
【解答】解：（1）
（2）12×8×5
＝96×5
＝480（立方厘米）
答：这人盒子的最大容积是480立方厘米。
【点评】此题主要考查对长方体的观察能力及求长方体体积（容积）的方法。
五、动手操作，我会画。（根据要求在答题卡指定的位置上作图。）
25．【分析】根据旋转的特征，三角形ABC绕点C顺时针旋转90°，点C的位置不动，这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
【解答】解：
【点评】图形旋转注意四要素：即原位置、旋转中心、旋转方向、旋转角。
六、解决问题，我能行。（将解题过程写在答题卡指定的位置上。）
26．【分析】用亲子组赛程路程除以全程组赛程的路程。
【解答】解：5÷60＝
答：亲子组赛程是全程组赛程的。
【点评】求一个数是另一个数的几分之几，用这个数除以另一个数。
27．【分析】用排水法来测量海豚雕塑摆件的体积，这块海豚雕塑摆件的体积等于下降的水的体积，用底面积乘下降的厘米数即可。
【解答】解：8×8×（7.5﹣6）
＝64×1.5
＝96（立方厘米）
答：这座雕塑的体积是96立方厘米。
【点评】此题主要考查某些实物体积的测量方法。
28．【分析】把工程总量看作单位“1”，用第一周完成了全工程的分率加第二周完成了全工程的分率即可。
【解答】解： +＝
答：两周完成了全工程的。
【点评】本题主要考查了分数加法，解题的关键是确定单位“1”。
29．【分析】先把40分钟化为小时，用小时减老师示范立定跳远动作要领用的时间，再减同学们进行练习用的时间，即可求出进行体能训练用的时间。
【解答】解：40分钟＝小时
﹣﹣
＝﹣
＝（小时）
答：同学们进行体能训练用了小时。
【点评】本题主要考查了分数的减法，解题的关键是掌握异分母分数减法法则。
30．【分析】（1）根据统计图可知，汕头在2006年的红树林累计造林面积是1600公顷，到2020年累计造林达到2000公顷。
（2）用2006年的红树林累计造林面积除以2020年累计造林面积，解答即可。
（3）根据统计图可知，从2015年至2020年的造林面积增长得最快。
【解答】解：（1）汕头在2006年的红树林累计造林面积是1600公顷，到2020年累计造林达到2000公顷。
（2）1600÷2000＝
答：2006年的红树林累计造林面积是2020年累计造林面积的。
（3）根据统计图可知，从2015年至 2020年的造林面积增长得最快。
故答案为：1600，2000；2015，2020。
【点评】本题关键是先读懂统计图，找出各个量之间的关系，再结合题意分析解答即可。
＝
12×0.5＝
＝
＝
＝
4÷9＝
＝
＝
＝
12×0.5＝6
＝
＝
＝
4÷9＝
＝
＝