浙江省宁波市鄞州区兴宁中学2022-—2023学年八年级上学期期中数学试题

这是一份浙江省宁波市鄞州区兴宁中学2022-—2023学年八年级上学期期中数学试题，共4页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．（2分）下列四个手机APP图标中，是轴对称图形的是（ ）
A．B．C．D．
2．（2分）已知一等腰三角形的两边长分别为4和8，则该三角形的周长是（ ）
A．18B．20C．22D．24
3．（2分）在数轴上表示不等式组﹣1＜x≤3，正确的是（ ）
A．B．
C．D．
4．（2分）如图，笑脸盖住的点的坐标可能为（ ）
A．（﹣2，3）B．（3，﹣4）C．（﹣4，﹣6）D．（5，2）
5．（2分）若实数a，b满足a＞b，则下列不等式一定成立的是（ ）
A．a＞b+2B．a﹣1＞b﹣2C．﹣a＞﹣bD．a2＞b2
6．（2分）能说明命题“对于任何实数a，都有＝a”是假命题的反例是（ ）
A．a＝﹣2B．a＝C．a＝1D．a＝
7．（2分）如图所示，OB平分∠CBA，OC平分∠ACB，设AB＝18，BC＝16，则△AMN的周长为（ ）
A．30B．33C．36D．39
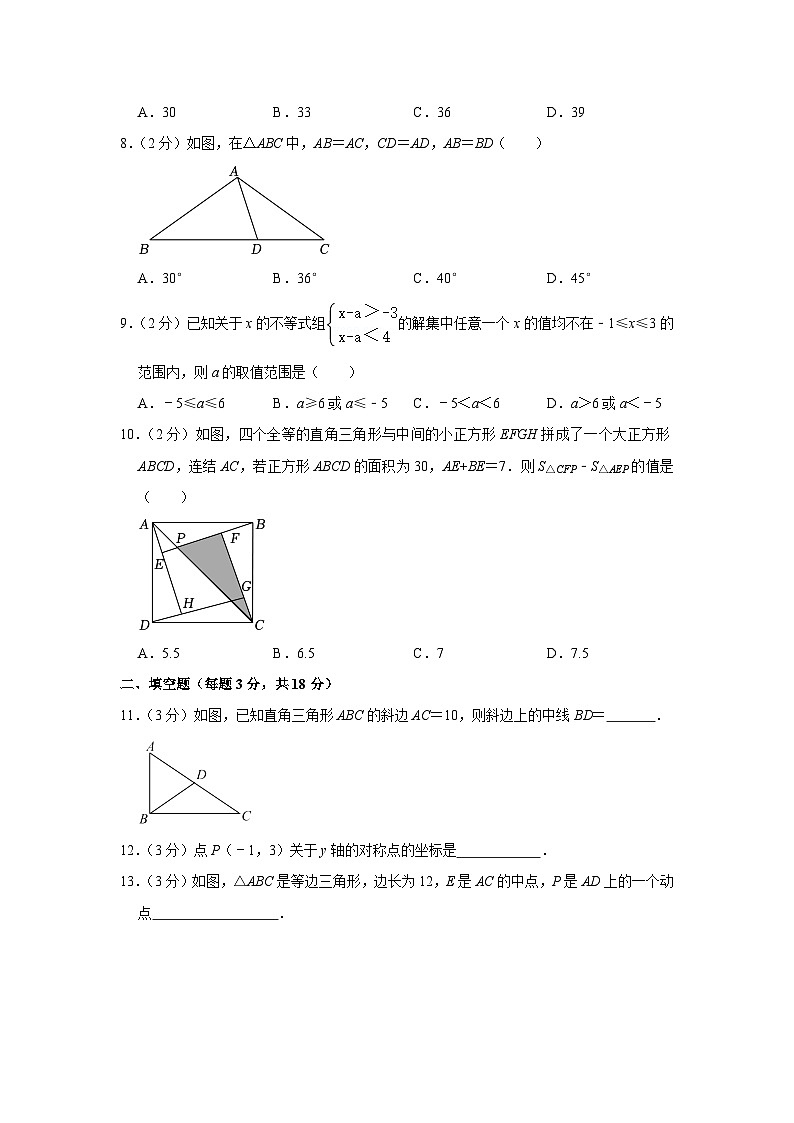
8．（2分）如图，在△ABC中，AB＝AC，CD＝AD，AB＝BD（ ）
A．30°B．36°C．40°D．45°
9．（2分）已知关于x的不等式组的解集中任意一个x的值均不在﹣1≤x≤3的范围内，则a的取值范围是（ ）
A．﹣5≤a≤6B．a≥6或a≤﹣5C．﹣5＜a＜6D．a＞6或a＜﹣5
10．（2分）如图，四个全等的直角三角形与中间的小正方形EFGH拼成了一个大正方形ABCD，连结AC，若正方形ABCD的面积为30，AE+BE＝7．则S△CFP﹣S△AEP的值是（ ）
A．5.5B．6.5C．7D．7.5
二、填空题（每题3分，共18分）
11．（3分）如图，已知直角三角形ABC的斜边AC＝10，则斜边上的中线BD＝ ．
12．（3分）点P（﹣1，3）关于y轴的对称点的坐标是 ．
13．（3分）如图，△ABC是等边三角形，边长为12，E是AC的中点，P是AD上的一个动点 ．
14．（3分）一部电梯的额定限载量为1000千克，两人要用电梯把一批重物从底层搬到顶层，这两个人的身体重量分别为60千克和80千克，问他们每次最多只能搬运多少箱重物？（注：两个人都必须进入电梯）设每次能搬运x箱 ．
15．（3分）如图，长方形ABCD中，AB＝8，长方形内有一个点P，连接AP，CP，已知∠APB＝90°，延长CP交AD于点E，则AE＝ ．
16．（3分）如图，△ABC和△ADE都是等腰直角三角形，∠BAC＝∠DAE＝90°，O为AC中点，若点D在直线BC上运动，则在点D运动过程中，线段OE的最小值是 ．
三、解答题
17．（6分）解下列不等式（组）：
（1）5x＞3（x﹣2）+2；
（2）．
18．（6分）如图，在6×6的网格中已经涂黑了三个小正方形，请按下列要求画图．
（1）在图1中涂黑一块小正方形，使涂黑的四个小正方形组成一个轴对称图形．
（2）在图2中涂黑两块小正方形，使涂黑的五个小正方形组成一个轴对称图形．
19．（6分）如图，在△ABC中，AB＝AC，E是AB上一点，且DE＝AE．
（1）求证：DE∥AC；
（2）若∠EDA＝24°，求∠C的度数．
20．（7分）某文具店最近有A，B两款毕业纪念册比较畅销，近两周的销售情况是：第一周A款销售数量是10本，销售总价是140元；第二周A款销售数量是20本，销售总价是320元．
（1）求A，B两款毕业纪念册的销售单价；
（2）若某班准备用不超过500元购买这两种款式的毕业纪念册共60本，求最多能够买多少本A款毕业纪念册．
21．（8分）如图所示，在平面直角坐标系中，已知A（0，1），B（2，0），C（4，3）．
（1）在平面直角坐标系中画出△ABC，以及与△ABC关于y轴对称的△DEF；
（2）△ABC的面积是 ；
（3）已知P为y轴上一点，若△ABP的面积为4，求点P的坐标．
22．（9分）阅读以下材料：对于三个数a，b，c，用M{a，b，c}表示这三个数的平均数，b，c}表示这三个数中最小的数．例如：M{﹣1，2，3}＝，2，3}＝﹣1；min{﹣1，2解决下列问题：
（1）min{，，}＝ 若min{2，2x+2，4﹣2x}＝2 ；
（2）①如果M{2，x+1，2x}＝min{2，2x}，求x；
②根据①，你发现了结论“如果M{a，b，c}＝min{a，b，那么 （填a，b，c的大小关系）”．证明你发现的结论；
③运用②的结论，填空：
若M{2x+y+2，x+2y，2x﹣y}＝min{2x+y+2，2x﹣y}，则x+y＝ ．
23．（8分）如图1，在等边△ABC中，线段AM为BC边上的高线．动点D在线段AM（点D与点A重合除外），以CD为一边且在CD的下方作等边△CDE，连结BE．
（1）若DM＝MC，则∠ACD＝ 度，∠BCE＝ 度；
（2）判断AD与BE是否相等，请说明理由；
（3）如图2，若AB＝16，P、Q两点在直线BE上且满足CP＝CQ＝10
24．（12分）如果一个三角形的两条边的和是第三边的两倍，则称这个三角形是“倍边三角形”．显然，等边三角形为倍边三角形．
（1）若倍边三角形的两条边长分别为5和7，则其第三边的长为 ．
（2）如图1，已知△ABC为倍边三角形，∠ACB＝90°，AC＝b，BC＝a，b＝5，求a的值；
（3）已知△ABC是倍边三角形，且∠ABC＝120°，BC＝2
2022-2023学年浙江省宁波市鄞州区兴宁中学八年级（上）期中数学试卷
参考答案与试题解析
一、选择题（每题2分，共20分）
1．（2分）下列四个手机APP图标中，是轴对称图形的是（ ）
A．B．C．D．
【分析】根据轴对称图形的概念进行判断即可．
【解答】解：A、不是轴对称图形；
B、是轴对称图形；
C、不是轴对称图形；
D、不是轴对称图形；
故选：B．
【点评】本题考查的是轴对称图形的概念：轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合．
2．（2分）已知一等腰三角形的两边长分别为4和8，则该三角形的周长是（ ）
A．18B．20C．22D．24
【分析】分两种情况讨论，由等腰三角形的性质和三角形三边关系可求解．
【解答】解：若4为腰，则三角形三边为：4，8，8，
∵4+2＝8，
∴4，7，8不能构成三角形，
故舍去，
若8为腰，则三角形三边为：8，8，8，
∵4+8＞8
∴6，8，8能构成三角形，
∴三角形的周长＝5+8+8＝20，
故选：B．
【点评】本题考查等腰三角形的性质，三角形三边关系，利用分类讨论思想解决问题是本题关键．
3．（2分）在数轴上表示不等式组﹣1＜x≤3，正确的是（ ）
A．B．
C．D．
【分析】把不等式组的解集在数轴上表示出来即可．
【解答】解：∵﹣1＜x≤3，
∴在数轴上表示为：
故选：C．
【点评】本题考查的是在数轴上表示不等式的解集，熟知“小于向左，大于向右”的法则是解答此题的关键．
4．（2分）如图，笑脸盖住的点的坐标可能为（ ）
A．（﹣2，3）B．（3，﹣4）C．（﹣4，﹣6）D．（5，2）
【分析】根据第二象限内点的横坐标小于零，纵坐标大于零，可得答案．
【解答】解：笑脸位于第二象限，故A符合题意；
故选：A．
【点评】本题考查了点的坐标，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（﹣，+）；第三象限（﹣，﹣）；第四象限（+，﹣）．
5．（2分）若实数a，b满足a＞b，则下列不等式一定成立的是（ ）
A．a＞b+2B．a﹣1＞b﹣2C．﹣a＞﹣bD．a2＞b2
【分析】通过举特例排除A，D；根据不等式的基本性质判断B，C．
【解答】解：A选项，如a＝2，b+2＝6，故该选项不符合题意；
B选项，∵a＞b，
∴a﹣1＞b﹣1＞b﹣6，故该选项符合题意；
C选项，∵a＞b，
∴﹣a＜﹣b，故该选项不符合题意；
D选项，如a＝﹣1，a2＜b5，故该选项不符合题意；
故选：B．
【点评】本题考查了不等式的基本性质，特别注意不等式的两边同时乘（或除以）同一个负数，不等号的方向改变．
6．（2分）能说明命题“对于任何实数a，都有＝a”是假命题的反例是（ ）
A．a＝﹣2B．a＝C．a＝1D．a＝
【分析】利用a＜0时，＝a不成立，从而可对各选项进行判断．
【解答】解：当a＝﹣2时，＝a不成立．
故选：A．
【点评】本题考查了命题：命题的“真”“假”是就命题的内容而言．任何一个命题非真即假．要说明一个命题的正确性，一般需要推理、论证，而判断一个命题是假命题，只需举出一个反例即可．
7．（2分）如图所示，OB平分∠CBA，OC平分∠ACB，设AB＝18，BC＝16，则△AMN的周长为（ ）
A．30B．33C．36D．39
【分析】根据BO平分∠CBA，CO平分∠ACB，且MN∥BC，可得出MO＝MC，NO＝NB，所以三角形AMN的周长是AB+AC．
【解答】解：∵BO平分∠CBA，CO平分∠ACB，
∴∠NBO＝∠OBC，∠OCM＝∠OCB，
∵MN∥BC，
∴∠MOB＝∠OBC，∠MOC＝∠OCB，
∴∠NBO＝∠NOB，∠MOC＝∠MCO，
∴MO＝MC，NO＝NB，
∵AB＝18，AC＝12，
∴△AMN的周长＝AM+MN+AN＝AB+AC＝18+12＝30．
故选：A．
【点评】本题考查了等腰三角形的判定和性质以及平行线的性质，是基础知识要熟练掌握．
8．（2分）如图，在△ABC中，AB＝AC，CD＝AD，AB＝BD（ ）
A．30°B．36°C．40°D．45°
【分析】求出∠BAD＝2∠CAD＝2∠B＝2∠C的关系，利用三角形的内角和是180°，求∠B，
【解答】解：∵AB＝AC，
∴∠B＝∠C，
∵AB＝BD，
∴∠BAD＝∠BDA，
∵CD＝AD，
∴∠C＝∠CAD，
∵∠BAD+∠CAD+∠B+∠C＝180°，
∴5∠B＝180°，
∴∠B＝36°
故选：B．
【点评】本题主要考查等腰三角形的性质，解题的关键是运用等腰三角形的性质得出∠BAD＝2∠CAD＝2∠B＝2∠C关系．
9．（2分）已知关于x的不等式组的解集中任意一个x的值均不在﹣1≤x≤3的范围内，则a的取值范围是（ ）
A．﹣5≤a≤6B．a≥6或a≤﹣5C．﹣5＜a＜6D．a＞6或a＜﹣5
【分析】根据解不等式组，可得不等式组的解集，根据不等式组的解集是与﹣1≤x≤3的关系，可得答案．
【解答】解：不等式组，得a﹣2＜x＜a+4，
由不等式组的解集中任意一个x的值均不在﹣1≤x≤3的范围内，得
a+3≤﹣1或a﹣3≥3，
解得a≤﹣5或a≥6，
故选：B．
【点评】本题考查了不等式的解集，利用解集中任意一个x的值均不在﹣1≤x≤3的范围内得出不等式是解题关键．
10．（2分）如图，四个全等的直角三角形与中间的小正方形EFGH拼成了一个大正方形ABCD，连结AC，若正方形ABCD的面积为30，AE+BE＝7．则S△CFP﹣S△AEP的值是（ ）
A．5.5B．6.5C．7D．7.5
【分析】依据题意，先证明△AEP≌△CGM（ASA），则S△AEP＝S△CGM，所以两三角形面积的差是中间正方形面积的一半，设AE＝x，BE＝7﹣x，根据勾股定理得：AE2+BE2＝AB2，x2+（7﹣x）2＝30，则2x2﹣14x＝﹣21，整体代入可得结论．
【解答】解：∵正方形ABCD的面积为30，
∴AB2＝30，
设AE＝x，
∵AE+BE＝7，
∴BE＝3﹣x，
Rt△AEB中，由勾股定理得：AE2+BE2＝AB8，
∴x2+（7﹣x）8＝30，
∴2x2﹣14x＝﹣19，
∵AH⊥BE，BE⊥CF，
∴AH∥CF，
∴∠EAP＝∠GCM，
∵“赵爽弦图”是由四个全等的直角三角形与中间的小正方形EFGH拼成的一个大正方形ABCD，
∴△AEB≌△CGD，
∴AE＝CG，
∴△AEP≌△CGM（ASA），
∴S△AEP＝S△CGM，EP＝MG，
∴S△CFP﹣S△AEP＝S△CFP﹣S△CGM＝S梯形FPMG＝（MG+PF）•FG＝S正方形EHGF，
∵S矩形EHGF＝S正方形ABCD﹣3S△AEB＝30﹣4×x•（7﹣x）＝30﹣2x（8﹣x）＝30﹣19＝11，
则S△CFP﹣S△AEP的值是5.5．
故选：A．
【点评】本题主要考查了勾股定理的证明，多边形的面积，首先要求学生正确理解题意，然后会利用勾股定理和三角形全等的性质解题．
二、填空题（每题3分，共18分）
11．（3分）如图，已知直角三角形ABC的斜边AC＝10，则斜边上的中线BD＝ 5 ．
【分析】根据直角三角形的性质计算即可．
【解答】解：∵直角△ABC的斜边AC＝10，
∴斜边上的中线BD＝AC＝，
故答案为：5．
【点评】本题考查的是直角三角形斜边上的中线，掌握在直角三角形中，斜边上的中线等于斜边的一半是解题的关键．
12．（3分）点P（﹣1，3）关于y轴的对称点的坐标是 （1，3） ．
【分析】根据关于y轴对称的点，纵坐标相同，横坐标互为相反数，可得答案．
【解答】解：P（﹣1，3）关于y轴的对称点的坐标是（8，
故答案为：（1，3）．
【点评】本题考查了关于x轴、y轴对称的点的坐标，解决本题的关键是掌握好对称点的坐标规律：关于x轴对称的点，横坐标相同，纵坐标互为相反数；关于y轴对称的点，纵坐标相同，横坐标互为相反数；关于原点对称的点，横坐标与纵坐标都互为相反数．
13．（3分）如图，△ABC是等边三角形，边长为12，E是AC的中点，P是AD上的一个动点 6 ．
【分析】先根据“两点之间线段最短”找到最小值，再根据勾股定理求解．
【解答】解：如图：
∵B、C关于直线AD对称，
∴PC+PE＝PB+PE≥BE，
∵△ABC是等边三角形，
∴AB＝AC＝BC＝12，∠BAE＝∠ABC＝60°，
∵E为AC的中点，
∴AE＝6，
由勾股定理得：BE＝6，
故答案为：6．
【点评】本题考查了最短路径问题，理解“两点之间线段最短”是解题的关键．
14．（3分）一部电梯的额定限载量为1000千克，两人要用电梯把一批重物从底层搬到顶层，这两个人的身体重量分别为60千克和80千克，问他们每次最多只能搬运多少箱重物？（注：两个人都必须进入电梯）设每次能搬运x箱 80+60+50x≤1000 ．
【分析】设可以搬运货物x箱．根据“额定限载量为1000千克”列出不等式即可．
【解答】解：设可以搬运货物x箱．
根据题意得，80+60+50x≤1000，
故答案为：80+60+50x≤1000．
【点评】本题考查了由实际问题抽象出一元一次不等式，根据各数量之间的关系，正确列出一元一次不等式是解题的关键．
15．（3分）如图，长方形ABCD中，AB＝8，长方形内有一个点P，连接AP，CP，已知∠APB＝90°，延长CP交AD于点E，则AE＝ ．
【分析】延长AP交CD于F，根据已知条件得到∠CPF+∠CPB＝90°，根据矩形的性质得到∠DAB＝∠ABC＝90°，BC＝AD＝3，根据余角的性质得到∠EAP＝∠ABP，推出AE＝PE，根据勾股定理即可得到结论．
【解答】解：如图，延长AP交CD于F，
∵∠APB＝90°，
∴∠FPB＝90°，
∴∠CPF+∠CPB＝90°，
∵四边形ABCD是矩形，
∴∠DAB＝∠ABC＝90°，BC＝AD＝6，
∴∠EAP+∠BAP＝∠ABP+∠BAP＝90°，
∴∠EAP＝∠ABP，
∵CP＝CB＝6，
∴∠CPB＝∠CBP，
∴∠CPF＝∠ABP＝∠EAP，
∵∠EPA＝∠CPF，
∴∠EAP＝∠APE，
∴AE＝PE，
∵CD8+DE2＝CE2，
∴42+（6﹣AE）5＝（6+AE）2，
解得：AE＝，
故答案为：．
【点评】本题考查了矩形的性质，等腰三角形的判定和性质，勾股定理，正确的识别图形是解题的关键．
16．（3分）如图，△ABC和△ADE都是等腰直角三角形，∠BAC＝∠DAE＝90°，O为AC中点，若点D在直线BC上运动，则在点D运动过程中，线段OE的最小值是 ．
【分析】取AB的中点为点Q，连接DQ，先证得△AQD≌△AOE，得出QD＝OE，根据点到直线的距离可知当QD⊥BC时，QD最小，然后根据等腰直角三角形的性质求得QD⊥BC时的QD的值，即可求得线段OE的最小值．
【解答】解：取AB的中点为点Q，连接DQ，
∵∠BAC＝∠DAE＝90°，
∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，
即∠BAD＝∠CAE，
∵AB＝AC＝4，O为AC中点，
∴AQ＝AO，
在△AQD和△AOE中，
，
∴△AQD≌△AOE（SAS），
∴QD＝OE，
∵点D在直线BC上运动，
∴当QD⊥BC时，QD最小，
∵△ABC是等腰直角三角形，
∴∠B＝45°，
∵QD⊥BC，
∴△QBD是等腰直角三角形，
∴QD＝QB，
∵QB＝AB＝8，
∴QD＝，
∴线段OE的最小值是为．
故答案为：．
【点评】本题考查了等腰直角三角形的性质、三角形全等的判定和性质、垂线段最短等知识，解题的关键是学会添加辅助线构建全等三角形，学会利用垂线段最短解决最值问题．
三、解答题
17．（6分）解下列不等式（组）：
（1）5x＞3（x﹣2）+2；
（2）．
【分析】（1）依次去括号、移项、合并同类项、系数化为1可得答案；
（2）分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集．
【解答】解：（1）∵5x＞3（x﹣6）+2，
∴5x＞4x﹣6+2，
2x﹣3x＞﹣6+6，
2x＞﹣4，
x＞﹣5；
（2）解不等式x﹣2（x﹣3）＞5，得：x＜2，
解不等式﹣（x+2）≤2﹣x，
则不等式组的解集为x＜2．
【点评】本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
18．（6分）如图，在6×6的网格中已经涂黑了三个小正方形，请按下列要求画图．
（1）在图1中涂黑一块小正方形，使涂黑的四个小正方形组成一个轴对称图形．
（2）在图2中涂黑两块小正方形，使涂黑的五个小正方形组成一个轴对称图形．
【分析】（1）根据轴对称图形的定义以及题目要求画出图形即可；
（2）根据轴对称图形的定义，以及题目要求画出图形即可．
【解答】解：（1）如图1中，图形即为所求．
（2）如图2中，图形即为所求．
【点评】本题考查利用轴对称设计图案，解题的关键是理解轴对称图形的定义，属于中考常考题型．
19．（6分）如图，在△ABC中，AB＝AC，E是AB上一点，且DE＝AE．
（1）求证：DE∥AC；
（2）若∠EDA＝24°，求∠C的度数．
【分析】（1）利用等腰三角形的三线合一性质可得∠CAD＝∠BAD，再利用等边对等角可得∠BAD＝∠EDA，从而可得∠CAD＝∠EDA，然后利用内错角相等，两直线平行可得DE∥AC，即可解答；
（2）利用（1）的结论可得∠CAD＝∠EDA＝24°，再利用等腰三角形的三线合一性质可得∠ADC＝90°，然后利用直角三角形的两个锐角互余进行计算，即可解答．
【解答】（1）证明：∵AB＝AC，AD是BC边上的中线，
∴∠CAD＝∠BAD，
∵DE＝AE，
∴∠BAD＝∠EDA，
∴∠CAD＝∠EDA，
∴DE∥AC；
（2）解：∵∠EDA＝24°，
∴∠CAD＝∠EDA＝24°，
∵AB＝AC，AD是BC边上的中线，
∴∠ADC＝90°，
∴∠C＝90°﹣∠CAD＝66°．
【点评】本题考查了等腰三角形的性质，平行线的判定与性质，熟练掌握等腰三角形的性质是解题的关键．
20．（7分）某文具店最近有A，B两款毕业纪念册比较畅销，近两周的销售情况是：第一周A款销售数量是10本，销售总价是140元；第二周A款销售数量是20本，销售总价是320元．
（1）求A，B两款毕业纪念册的销售单价；
（2）若某班准备用不超过500元购买这两种款式的毕业纪念册共60本，求最多能够买多少本A款毕业纪念册．
【分析】（1）设A款毕业纪念册的销售单价为x元，B款毕业纪念册的销售单价为y元，根据“第一周A款销售数量是10本，B款销售数量是5本，销售总价是140元；第二周A款销售数量是20本，B款销售数量是15本，销售总价是320元”，可列出关于x，y的二元一次方程组，解之即可求出结论；
（2）设购买m本A款毕业纪念册，则购买（60﹣m）本B款毕业纪念册，利用总价＝单价×数量，结合总价不超过500元，可列出关于m的一元一次不等式，解之取其中的最大值，即可得出结论．
【解答】解：（1）设A款毕业纪念册的销售单价为x元，B款毕业纪念册的销售单价为y元，
根据题意得：，
解得：．
答：A款毕业纪念册的销售单价为10元，B款毕业纪念册的销售单价为2元；
（2）设购买m本A款毕业纪念册，则购买（60﹣m）本B款毕业纪念册，
根据题意得：10m+8（60﹣m）≤500，
解得：m≤10，
∴m的最大值为10．
答：最多能够买10本A款毕业纪念册．
【点评】本题考查了二元一次方程组的应用以及一元一次不等式的应用，解题的关键是：（1）找准等量关系，正确列出二元一次方程组；（2）根据各数量之间的关系，正确列出一元一次不等式．
21．（8分）如图所示，在平面直角坐标系中，已知A（0，1），B（2，0），C（4，3）．
（1）在平面直角坐标系中画出△ABC，以及与△ABC关于y轴对称的△DEF；
（2）△ABC的面积是 4 ；
（3）已知P为y轴上一点，若△ABP的面积为4，求点P的坐标．
【分析】（1）先利用关于y轴对称的点的坐标特征得到D、E、F的坐标，然后描点即可；
（2）用一个矩形的面积分别减去三个直角三角形的面积去计算△ABC的面积；
（3）设P点坐标为（0，t），利用三角形面积公式得到×|t﹣1|×2＝4，然后求出t得到P点坐标．
【解答】解：（1）如图，△ABC和△DEF为所作；
（2）△ABC的面积＝4×3﹣×2×4﹣×2×4＝4，
故答案为：4；
（3）设P点坐标为（4，t），
∵△ABP的面积为4，
∴，
解得t＝﹣3或5，
∴P点坐标为（7，﹣3）或（0．
【点评】本题考查了作图﹣轴对称变换：几何图形都可看作是由点组成，我们在画一个图形的轴对称图形时，也是先从确定一些特殊的对称点开始的．也考查了三角形面积公式．
22．（9分）阅读以下材料：对于三个数a，b，c，用M{a，b，c}表示这三个数的平均数，b，c}表示这三个数中最小的数．例如：M{﹣1，2，3}＝，2，3}＝﹣1；min{﹣1，2解决下列问题：
（1）min{，，}＝ 若min{2，2x+2，4﹣2x}＝2 0≤x≤1 ；
（2）①如果M{2，x+1，2x}＝min{2，2x}，求x；
②根据①，你发现了结论“如果M{a，b，c}＝min{a，b，那么 a＝b＝c （填a，b，c的大小关系）”．证明你发现的结论；
③运用②的结论，填空：
若M{2x+y+2，x+2y，2x﹣y}＝min{2x+y+2，2x﹣y}，则x+y＝ ﹣4 ．
【分析】①M{a，b，c}表示这a，b，c三个数的平均数，即求的值；
②min{a，b，c}表示这a，b，c三个数中最小的数，即比较三个数的大小哪一个最小．
【解答】解：（1）min{，，}＝；
由min{3，2x+2，得，即7≤x≤1．
（2）①∵M{2，x+6，x+1，∴，即，∴x＝1
②证明：由M{a，b，c}＝min{a，b，可令；
又∵，解之
得：a+c≤8b ⑥，a+b≤2c⑦；
由⑤⑥可得c≤b；由⑤⑦可得b≤c；
∴b＝c；将b＝c代入⑤得c＝a；
∴a＝b＝c．
③据②可得，
解之得y＝﹣1，x＝﹣6，
∴x+y＝﹣4．
【点评】本题解决的关键是读懂题意，据题意结合方程和不等式去求解，考查综合应用能力．
23．（8分）如图1，在等边△ABC中，线段AM为BC边上的高线．动点D在线段AM（点D与点A重合除外），以CD为一边且在CD的下方作等边△CDE，连结BE．
（1）若DM＝MC，则∠ACD＝ 15 度，∠BCE＝ 15 度；
（2）判断AD与BE是否相等，请说明理由；
（3）如图2，若AB＝16，P、Q两点在直线BE上且满足CP＝CQ＝10
【分析】（1）由等边三角形的性质和等腰直角三角形的性质求解即可；
（2）证△ACD≌△BCE（SAS），即可得出结论；
（3）过点C作CN⊥BQ于点N，由等腰三角形的性质得PQ＝2PN，再由勾股定理求出PN＝6，即可求解．
【解答】解：（1）∵△ABC和△CDE是等边三角形，
∴BC＝AC，∠ACB＝∠DCE＝60°，
∵线段AM为BC边上的高线，
∴AM⊥BC，
∴∠AMC＝90°，
∵DM＝MC，
∴△CDM是等腰直角三角形，
∴∠MCD＝45°，
∴∠ACD＝∠ACB﹣∠MCD＝60°﹣45°＝15°，∠BCE＝∠DCE﹣∠MCD＝60°﹣45°＝15°，
故答案为：15，15；
（2）AD＝BE．理由如下：
∵△ABC和△CDE都是等边三角形，
∴BC＝AC，∠ACB＝∠DCE＝60°，
∴∠ACB﹣∠MCD＝∠DCE﹣∠MCD，
即∠ACD＝∠BCE，
∴△ACD≌△BCE（SAS），
∴AD＝BE；
（3）如图，过点C作CN⊥BQ于点N，
∵CP＝CQ，
∴PQ＝2PN，
∵△ABC是等边三角形，AM是中线，
∴BC＝AB＝16，CM⊥AD，，
∴CN＝CM＝6（全等三角形对应边上的高相等），
∵CP＝CQ＝10，
∴，
∴PQ＝2PN＝12．
【点评】本题是三角形综合题目，考查了等边三角形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、勾股定理的应用等知识，本题综合性强，熟练掌握等边三角形的性质和等腰直角三角形的判定与性质，证明△ACD≌△BCE是解题的关键．
24．（12分）如果一个三角形的两条边的和是第三边的两倍，则称这个三角形是“倍边三角形”．显然，等边三角形为倍边三角形．
（1）若倍边三角形的两条边长分别为5和7，则其第三边的长为 3或6或9 ．
（2）如图1，已知△ABC为倍边三角形，∠ACB＝90°，AC＝b，BC＝a，b＝5，求a的值；
（3）已知△ABC是倍边三角形，且∠ABC＝120°，BC＝2
【分析】（1）依据题意，根据“倍边三角形”的定义进行分类讨论即可得解；
（2）由题意，c＞b≥a，则a+c＝2b，即c＝10﹣a，进而求解；
（3）作AD⊥BC于D，设BC＝a＝2，AC＝b，AB＝c，则，，再分类求解即可．
【解答】解：（1）设第三边长是x，
∴5+7＝2x或5+x＝2×4或7+x＝2×7，
∴x＝6或9或3．
∴第三边的长为3或6或7．
（2）由题意，∵c＞b≥a，
∴a+c＝2b，即c＝10﹣a，
∵a2+b8＝c2，
∴a2+62＝（10﹣a）2，
∴；
（3）作AD⊥BC于D，设BC＝a＝2，AB＝c，
则，，
（I）当a≤c＜b时，a+b＝7c，
∴b＝2c﹣2，
∵AD5+CD2＝AC2，
即，
∴，
∴，c2＝0（舍），
∴，
（Ⅱ）当c≤a＜b时，b+c＝2a，
∴b＝4﹣c，
同理可得：，
综上，△ABC的面积为：或．
【点评】本题为三角形综合运用，涉及到新定义、三角形的边角关系、勾股定理的运用、面积的计算等，有一定的综合性，难度适中．
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2023/11/6 13:51:31；用户：娄老师；邮箱：15225657626；学号：48669677