辽宁省抚顺市清原满族自治县2022-2023学年八年级上学期期中教学质量检测数学试卷(含解析)

这是一份辽宁省抚顺市清原满族自治县2022-2023学年八年级上学期期中教学质量检测数学试卷(含解析)，共13页。试卷主要包含了选择题，填空题等内容，欢迎下载使用。

一、选择题（下列各题的备选答案中，只有一个答案是正确的，请将正确答案的序号填入题后相应的括号内，每小题2分，共20分）
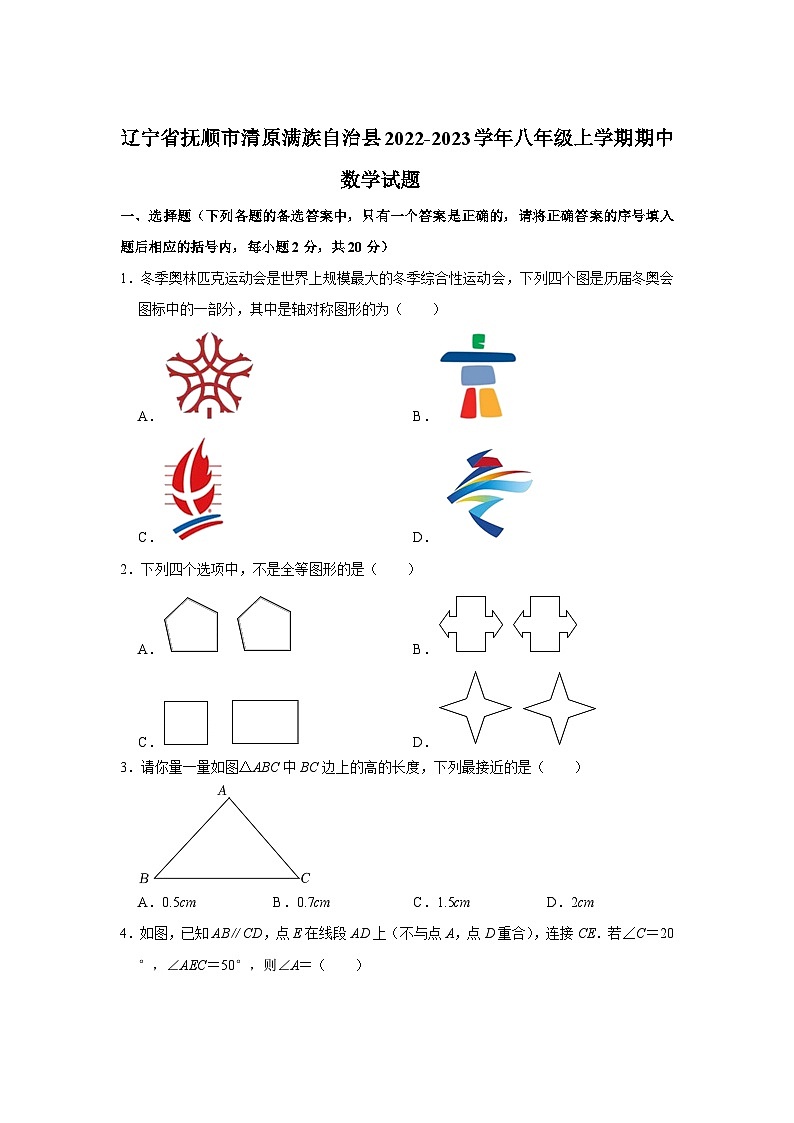
1．冬季奥林匹克运动会是世界上规模最大的冬季综合性运动会，下列四个图是历届冬奥会图标中的一部分，其中是轴对称图形的为（ ）
A．B．
C．D．
2．下列四个选项中，不是全等图形的是（ ）
A．B．
C．D．
3．请你量一量如图△ABC中BC边上的高的长度，下列最接近的是（ ）
A．0.5cmB．0.7cmC．1.5cmD．2cm
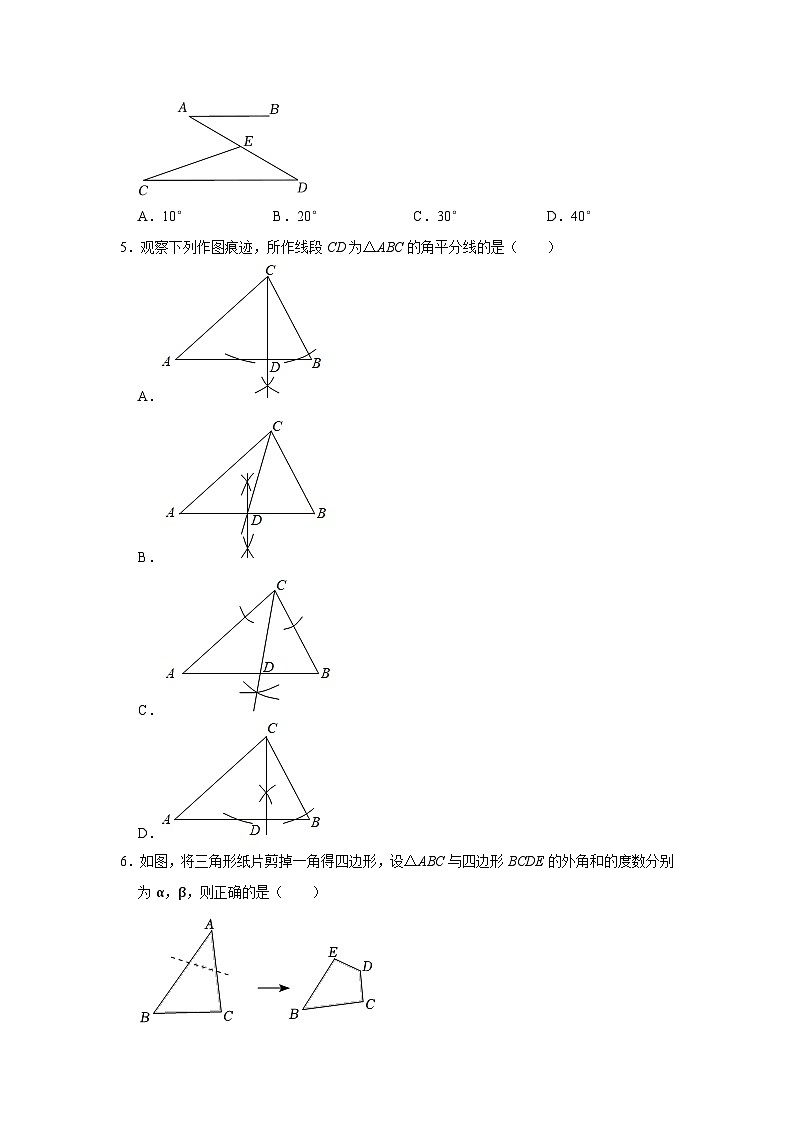
4．如图，已知AB∥CD，点E在线段AD上（不与点A，点D重合），连接CE．若∠C＝20°，∠AEC＝50°，则∠A＝（ ）
A．10°B．20°C．30°D．40°
5．观察下列作图痕迹，所作线段CD为△ABC的角平分线的是（ ）
A．
B．
C．
D．
6．如图，将三角形纸片剪掉一角得四边形，设△ABC与四边形BCDE的外角和的度数分别为α，β，则正确的是（ ）
A．α﹣β＝0B．α﹣β＜0
C．α﹣β＞0D．无法比较α与β的大小
7．如图，OA平分∠BOD，AC⊥OB于点C，且AC＝2，已知点A到y轴的距离是3，那么点A关于y轴对称的点的坐标为（ ）
A．（﹣3，﹣2）B．（﹣2，﹣3）C．（3，2）D．（2，3）
8．如图，小明家仿古家具的一块三角形状的玻璃坏了，需要重新配一块．小明通过电话给玻璃店老板提供相关数据，为了方便表述，将该三角形记为△ABC，提供下列各组元素的数据，配出来的玻璃不一定符合要求的是（ ）
A．AB，BC，CAB．AB，BC，∠BC．AB，AC，∠BD．∠A，∠B，BC
9．如图，已知每个小方格的边长为1，A，B两点都在小方格的顶点上，请在图中找一个顶点C，使△ABC为等腰三角形，则这样的顶点C有（ ）
A．8个B．7个C．6个D．5个
10．已知：如图，在△ABC，△ADE中，∠BAC＝∠DAE＝90°，AB＝AC，AD＝AE，点C，D，E三点在同一条直线上，连接BD，BE．以下四个结论：
①BD＝CE；②∠ACE+∠DBC＝45°；③BD⊥CE；④∠BAE+∠DAC＝180°．
其中结论正确的个数是（ ）
A．1B．2C．3D．4
二、填空题（每小题2分，共16分）
11．已知三角形的两边长分别为3和6，则这个三角形的第三边长可以是 （写出一个即可）．
12．已知一个n边形的每一个外角都为30°，则n等于 ．
13．在△ABC中，∠C＝90°，∠B＝30°，AB＝4，AC＝ ．
14．如图所示，点O在一块直角三角板ABC上（其中∠ABC＝30°），OM⊥AB于点M，ON⊥BC于点N，若OM＝ON，则∠ABO＝ 度．
15．将一副直角三角板如图放置，已知∠E＝60°，∠C＝45°，EF∥BC，则∠BND＝ °．
16．如图，在△ABC中，∠ACB＝90°，AC＜BC．分别以点A，B为圆心，大于AB的长为半径画弧，两弧交于D，E两点，直线DE交BC于点F，连接AF．以点A为圆心，AF为半径画弧，交BC延长线于点H，连接AH．若BC＝3，则△AFH的周长为 ．
17．如图所示，已知∠MON＝60°，正五边形ABCDE的顶点A、B在射线OM上，顶点E在射线ON上，则∠AEO＝ 度．
18．如图，在△ABC中，AC＝BC，△ADE的顶点D在AB边上，点E在△ABC内部，∠E＝∠EAB＝60°，CF平分∠ACB交DE于点F，若AE＝a，EF＝b，则AB的长为 （用含a，b的代数式表示）．
三.（19题6分、20题7分，共13分）
19．（6分）在括号里填出相应的理由．
已知：∠ACE是△ABC的外角，∠1＝∠2，CD∥AB．
求证：AC＝BC．
证明：∵CD∥AB，
∴∠1＝∠A（ ）．
∠2＝∠B（ ）．
∵∠1＝∠2，
∴∠A＝∠B，
∴AC＝BC（ ）．
20．（7分）如图，在△ABC中，点D在边BC上，CD＝AB，DE∥AB，∠DCE＝∠A．求证：DE＝BC．
四、（每小题8分，共16分）
21．（8分）图①、图②、图③均是3×3的正方形网格，每个小正方形的边长为1，每个小正方形的顶点称为格点，线段AB的端点均在格点上，只用无刻度的直尺，在给定的网格中，按下列要求以AB为边画△ABC．
要求：
（1）在图①中画一个钝角三角形，在图②中画一个直角三角形，在图③中画一个锐角三角形；
（2）三个图中所画的三角形的面积均不相等；
（3）点C在格点上．
22．（8分）如图1是小军制作的燕子风筝，燕子风筝的骨架图如图2所示，AB＝AE，AC＝AD，∠BAD＝∠EAC，∠C＝50°，求∠D的大小．
五、（23题8分，24题9分，共17分）
23．（8分）如图，有两个长度相等的滑梯AB与DE（即AB＝DE），滑梯AB的高BC与滑梯DE的水平方向EF的长度相等（即BC＝EF），且BC⊥AC，DF⊥EF，问两个滑梯的倾斜角∠A与∠E的大小有什么关系？请说明理由．
24．（9分）如图，BE是△ABC的角平分线，在AB上取点D，使DB＝DE．
（1）求证：DE∥BC；
（2）若∠A＝65°，∠AED＝45°，求∠EBC的度数．
六、（每小题9分，共18分）
25．（9分）如图，△ABC中，∠ACB＝90°，∠B＝30°，AD平分∠CAB，延长AC至E，使CE＝AC．
（1）求证：DE＝DB；
（2）连接BE，试判断△ABE的形状，并说明理由．
26．（9分）（1）如图1，在△ABC中，D是AB上一点，∠ADC＝∠ACB．求证：∠ACD＝∠ABC．
（2）在原有问题条件不变的情况下，增加下面的条件，并提出新问题，请你解答．
如图2，延长CA至点E，使CE＝BD，BE与CD的延长线相交于点F，点G，H分别在BF，BC上，BG＝CD，∠BGH＝∠BCF．在图中找出与BH相等的线段，并证明．
辽宁省抚顺市清原满族自治县2022-2023学年八年级上学期期中数学答案
一、选择题（下列各题的备选答案中，只有一个答案是正确的，请将正确答案的序号填入题后相应的括号内，每小题2分，共20分）
1．
解析：解：选项B、C、D不能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以不是轴对称图形，
选项A能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以是轴对称图形，
故选：A．
2．
解析：解：A、两个图形是全等图形，不符合题意；
B、两个是全等图形，不符合题意；
C、两个图形大小不同，不是全等图形，符合题意；
D、两个图形是全等图形，不符合题意；
故选：C．
3．
解析：解：过点A作AD⊥BC于D，
用刻度尺测量AD的长度，更接近2cm，
故选：D．
4．
解析：解：∵∠AEC为△CED的外角，且∠C＝20°，∠AEC＝50°，
∴∠AEC＝∠C+∠D，即50°＝20°+∠D，
∴∠D＝30°，
∵AB∥CD，
∴∠A＝∠D＝30°．
故选：C．
5．
解析：解：根据基本作图，A、D选项中为过C点作AB的垂线，B选项作AB的垂直平分线得到AB边上的中线CD，C选项作CD平分∠ACB．
故选：C．
6．
解析：解：∵任意多边形的外角和为360°，
∴α＝β＝360°．
∴α﹣β＝0．
故选：A．
7．
解析：解：过点A作AE⊥x轴，垂足为E，
∵OA平分∠BOD，AC⊥OB，AE⊥x轴，
∴AC＝AE＝2，
∵点A到y轴的距离是3，
∴A（﹣3，2），
∴点A关于Y轴对称的点的坐标为：（3，2），
故选：C．
8．
解析：解：A．利用三角形三边对应相等，两三角形全等，三角形形状确定，故此选项不合题意；
B．利用三角形两边、且夹角对应相等，两三角形全等，三角形形状确定，故此选项不合题意；
C．AB，AC，∠B，无法确定三角形的形状，故此选项符合题意；
D．根据∠A，∠B，BC，三角形形状确定，故此选项不合题意；
故选：C．
9．
解析：解：当AB为底时，作AB的垂直平分线，可找出格点C的个数有5个，
当AB为腰时，分别以A、B点为顶点，以AB为半径作弧，可找出格点C的个数有3个；
∴这样的顶点C有8个．
故选：A．
10．
解析：解：①∵∠BAC＝∠DAE＝90°，
∴∠BAC+∠CAD＝∠DAE+∠CAD，即∠BAD＝∠CAE，
∵在△BAD和△CAE中，，
∴△BAD≌△CAE（SAS），
∴BD＝CE，本选项正确；
②∵△ABC为等腰直角三角形，
∴∠ABC＝∠ACB＝45°，
∴∠ABD+∠DBC＝45°，
∵△BAD≌△CAE，
∴∠ABD＝∠ACE，
∴∠ACE+∠DBC＝45°，本选项正确；
③∵∠ABD+∠DBC＝45°，
∴∠ACE+∠DBC＝45°，
∴∠DBC+∠DCB＝∠DBC+∠ACE+∠ACB＝90°，
则BD⊥CE，本选项正确；
④∵∠BAC＝∠DAE＝90°，
∴∠BAE+∠DAC＝360°﹣90°﹣90°＝180°，故此选项正确，
故选：D．
二、填空题（每小题2分，共16分）
11．
解析：解：根据三角形的三边关系，得
第三边应大于6﹣3＝3，而小于6+3＝9，
故第三边的长度3＜x＜9，这个三角形的第三边长可以是4．
故答案为：4．
12．
解析：解：∵一个n边形的每一个外角都为30°，任意多边形的外角和都是360°，
∴n＝360°÷30°＝12．
故答案为：12．
13．
解析：解：如图，
∵在△ABC中，∠C＝90°，∠B＝30°，
∴AB＝2AC，
∵AB＝4，
∴AC＝2，
故答案为：2．
14．
解析：解：方法一：∵OM⊥AB，ON⊥BC，
∴∠OMB＝∠ONB＝90°，
在Rt△OMB和Rt△ONB中，
，
∴Rt△OMB≌Rt△ONB（HL），
∴∠OBM＝∠OBN，
∵∠ABC＝30°，
∴∠ABO＝15°．
方法二：∵OM⊥AB，ON⊥BC，
又∵OM＝ON，
∴OB平分∠ABC，
∴∠OBM＝∠OBN，
∵∠ABC＝30°，
∴∠ABO＝15°．
故答案为：15．
15．
解析：解：∵∠E＝60°，∠C＝45°，
∴∠F＝30°，∠B＝45°，
∵EF∥BC，
∴∠NDB＝∠F＝30°，
∴∠BND＝180°﹣∠B﹣∠NDB＝180°﹣45°﹣30°＝105°，
故答案为：105．
16．
解析：解：由基本作图方法得出：DE垂直平分AB，
则AF＝BF，
可得AF＝AH，AC⊥FH，
∴FC＝CH，
∴AF+FC＝BF+FC＝AH+CH＝BC＝3，
∴△AFH的周长为：AF+FC+CH+AH＝2BC＝6．
故答案为：6．
17．
解析：解：∵五边形ABCDE是正五边形，
∴∠EAB＝＝108°，
∵∠EAB是△AEO的外角，
∴∠AEO＝∠EAB﹣∠MON＝108°﹣60°＝48°，
故答案为：48．
18．
解析：解：延长CF交AB于点G，
∵∠E＝∠EAB＝60°，
∴∠ADE＝180°﹣∠E﹣∠EAB＝60°，
∴∠E＝∠EAB＝∠ADE＝60°，
∴△ADE是等边三角形，
∴AE＝AD＝ED＝a，
∵EF＝b，
∴DF＝ED﹣EF＝a﹣b，
∵AC＝BC，CF平分∠ACB，
∴AB＝2AG，∠CGB＝90°，
∴∠DFG＝90°﹣∠ADE＝30°，
∴DG＝DF＝（a﹣b），
∴AG＝AD﹣DG＝a﹣（a﹣b）＝a+b，
∴AB＝2AG＝a+b，
故答案为：a+b．
三.（19题6分、20题7分，共13分）
19．
解析：证明：∵CD∥AB，
∴∠1＝∠A（两直线平行，内错角相等）．
∠2＝∠B（两直线平行，同位角相等）．
∵∠1＝∠2，
∴∠A＝∠B，
∴AC＝BC（等角对等边）．
故答案为：两直线平行，内错角相等；两直线平行，同位角相等；等角对等边．
20．
解析：证明：∵DE∥AB，
∴∠EDC＝∠B，
在△CDE和△ABC中，
，
∴△CDE≌△ABC（ASA），
∴DE＝BC．
四、（每小题8分，共16分）
21．
解析：解：如图所示：即为符合条件的三角形．
22．
解析：解：∵∠BAD＝∠EAC，
∴∠BAD+∠CAD＝∠EAC+∠CAD，即∠BAC＝∠EAD，
在△BAC与△EAD中，
，
∴△BAC≌△EAD（SAS），
∴∠D＝∠C＝50°．
五、（23题8分，24题9分，共17分）
23．
解析：解：∠A与∠E互余，理由如下：
在Rt△ABC和Rt△DEF中，
，
∴Rt△ABC≌Rt△DEF（HL），
∴∠A＝∠EDF，
又∵∠DEF+∠EDF＝90°，
∴∠E+∠A＝90°，
即两滑梯的倾斜角∠A与∠F互余．
24．
解析：（1）证明：∵BE是△ABC的角平分线，
∴∠DBE＝∠EBC，
∵DB＝DE，
∴∠DEB＝∠DBE，
∴∠DEB＝∠EBC，
∴DE∥BC；
（2）解：∵DE∥BC，
∴∠C＝∠AED＝45°，
在△ABC中，∠A+∠ABC+∠C＝180°，
∴∠ABC＝180°﹣∠A﹣∠C＝180°﹣65°﹣45°＝70°．
∵BE是△ABC的角平分线，
∴∠DBE＝∠EBC＝．
六、（每小题9分，共18分）
25．
解析：（1）证明：∵∠ACB＝90°，∠ABC＝30°，
∴BC⊥AE，∠CAB＝60°，
∵AD平分∠CAB，
∴∠DAB＝∠CAB＝30°＝∠ABC，
∴DA＝DB，
∵CE＝AC，
∴BC是线段AE的垂直平分线，
∴DE＝DA，
∴DE＝DB；
（2）△ABE是等边三角形；理由如下：
连接BE，如图：
∵BC是线段AE的垂直平分线，
∴BA＝BE，
即△ABE是等腰三角形，
又∵∠CAB＝60°，
∴△ABE是等边三角形．
26．
解析：证明：（1）如图1，
∵∠ADC＝∠ACB，∠ADC＝∠ABC+∠BCD，∠ACB＝∠ACD+∠BCD，
∴∠ABC+∠BCD＝∠ACD+∠BCD，
∴∠ACD＝∠ABC；
（2）BH＝EF，理由如下：
如图2，在BC上取一点T，使GH＝CT，连接DT，
在△BGH和△DCT中，
，
∴△BGH≌△DCT（SAS），
∴BH＝DT，∠GBH＝∠CDT，
∵∠CDT+∠FDT＝180°，
∴∠GBH+∠FDT＝180°，
∴∠BFD+∠BTD＝180°，
∴∠CFE+∠BFD＝180°，
∴∠CFE＝∠BTD，
在△CEF和△BDT中，
，
∴△CEF≌△BDT（AAS），
∴EF＝DT，
∴EF＝BH．