




- 北师大版数学七年级下册期末复习考点串讲+题型专训专题02 相交线与平行线(2份打包,原卷版+含解析) 试卷 0 次下载
- 北师大版数学七年级下册期末复习考点串讲+题型专训专题03 变量之间的关系(2份打包,原卷版+含解析) 试卷 1 次下载
- 北师大版数学七年级下册期末复习考点串讲+题型专训专题04 三角形(2份打包,原卷版+含解析) 试卷 1 次下载
- 北师大版数学七年级下册期末复习考点串讲+题型专训专题05 全等三角形证明方法:倍长中线(2份打包,原卷版+含解析) 试卷 0 次下载
- 北师大版数学七年级下册期末复习考点串讲+题型专训专题06 全等三角形证明方法:手拉手模型(2份打包,原卷版+含解析) 试卷 1 次下载
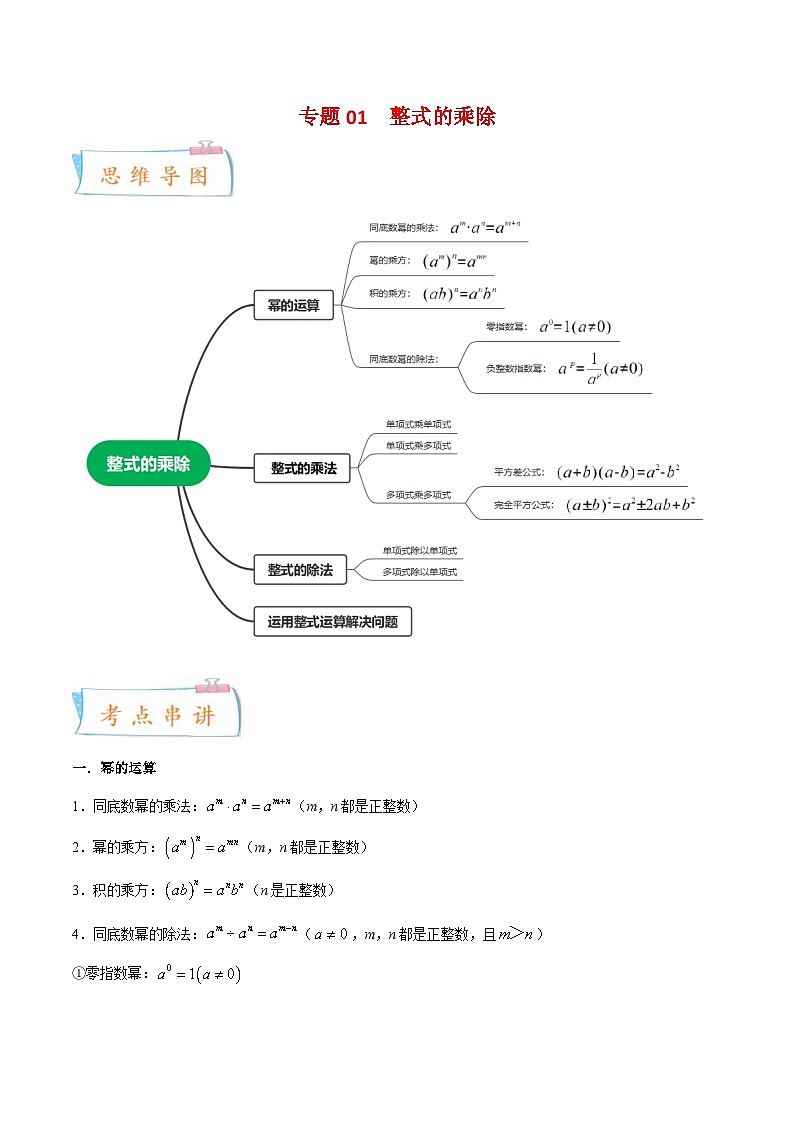
北师大版数学七年级下册期末复习考点串讲+题型专训专题01 整式的乘除(2份打包,原卷版+含解析)
展开一.幂的运算
1.同底数幂的乘法: SKIPIF 1 < 0 (m,n都是正整数)
2.幂的乘方: SKIPIF 1 < 0 (m,n都是正整数)
3.积的乘方: SKIPIF 1 < 0 (n是正整数)
4.同底数幂的除法: SKIPIF 1 < 0 ( SKIPIF 1 < 0 ,m,n都是正整数,且 SKIPIF 1 < 0 )
①零指数幂: SKIPIF 1 < 0
②负整数指数幂: SKIPIF 1 < 0 ( SKIPIF 1 < 0 ,p是正整数)
二.整式的乘法
1.单项式乘单项式:单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余字母连同它的指数不变,作为积的因式.
2.单项式乘多项式:单项式与多项式相乘,就是根据分配律用单项式去乘多项式的每一项,再把所得的积相加.
3.多项式乘多项式:多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
4.两个乘法公式:
①平方差公式: SKIPIF 1 < 0
②完全平方公式: SKIPIF 1 < 0
三.整式的除法
1.单项式除以单项式:单项式与单项式相除,把它们的系数、同底数幂分别相除,作为商的因式.对于只在被除式里含有的字母,则连同它的指数一起作为商的一个因式.
2.多项式除以单项式:多项式除以单项式,先把这个多项式的每一项分别除以单项式,再把所得的商相加.
【专题过关】
一.幂的运算(共4小题)
1.计算 SKIPIF 1 < 0 的结果是( )
【答案】C
【分析】利用幂的乘法公式“ SKIPIF 1 < 0 ”求解.
【详解】解: SKIPIF 1 < 0 .
故选:C.
【点睛】本题考查了同底数幂的乘法运算,直接套用公式 SKIPIF 1 < 0 即可.
2.下列运算中,正确的是( )
【答案】C
【分析】根据同底数幂的乘法法则可判断选项A,D,根据合并同类项可判断选项B,根据幂的乘方法则可判断选项C.
【详解】解:A. SKIPIF 1 < 0 ,选项A不符合题意;
B. SKIPIF 1 < 0 不是同类项,不能合并,选项B不符合题意;
C. SKIPIF 1 < 0 ,选项C符合题意;
D. SKIPIF 1 < 0 ,选项D不符合题意;
故选:C.
【点睛】本题主要考查了同底数幂的乘法,幂的乘方以及合并同类项,掌握同底数幂的乘法法则,幂的乘
方法则以及合并同类项法则是解题的关键.
3.计算 SKIPIF 1 < 0 的结果是( )
【答案】B
【分析】根据积的乘方运算以及幂的乘方运算即可求出答案.
【详解】解:原式 SKIPIF 1 < 0 ,
故选:B.
【点睛】本题考查幂的乘方运算以及积的乘方运算,解题的关键是熟练运用幂的乘方运算以及积的乘方运
算,本题属于基础题型.
4.下列运算正确的是( )
【答案】D
【分析】利用合并同类项的法则,同底数幂的除法的法则,幂的乘方与积的乘方的法则对各项进行运算即可.
【详解】解:A、 SKIPIF 1 < 0 ,故A不符合题意;
B、 SKIPIF 1 < 0 ,故B不符合题意;
C、 SKIPIF 1 < 0 ,故C不符合题意;
D、 SKIPIF 1 < 0 ,故D符合题意;
故选:D.
【点睛】本题主要考查幂的乘方与积的乘方,同底数幂的除法,合并同类项,解答的关键是对相应的运算法则的掌握.
二.幂的运算的逆用(共5题)
5.若 SKIPIF 1 < 0 ,则m= .
【答案】3
【分析】同底数幂相乘,底数不变,指数相加,据此解答即可.
【详解】解:因为 SKIPIF 1 < 0 ,
所以 SKIPIF 1 < 0 ,
解得 SKIPIF 1 < 0 .
故答案为:3.
【点睛】本题主要考查了同底数幂的乘法,熟记幂的运算法则是解答本题的关键.
6.若 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 = .
【答案】b
【分析】利用同底数幂的乘法的法则进行求解即可.
【详解】解:∵ SKIPIF 1 < 0 , SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 ,
SKIPIF 1 < 0 ,
SKIPIF 1 < 0 .
故答案为:b.
【点睛】本题主要考查同底数幂的乘法,解答的关键是对相应的运算法则的掌握.
7.若 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 的值为 .
【答案】35
【分析】根据同底数幂乘法及幂的乘方的逆运算解答即可.
【详解】解:∵ SKIPIF 1 < 0 , SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 ,
故答案为:35.
【点睛】本题考查了同底数幂乘法、幂的乘方,运用法则逆运算是解题的关键.
8.计算: SKIPIF 1 < 0 = .
【答案】 SKIPIF 1 < 0
【分析】根据积的乘方的逆运算计算即可.
【详解】解: SKIPIF 1 < 0
= SKIPIF 1 < 0
= SKIPIF 1 < 0
= SKIPIF 1 < 0 .
故答案为: SKIPIF 1 < 0 .
【点睛】本题主要考查了积的乘方的逆运算及有理数的乘方运算,掌握积的乘方的逆运算及有理数的乘方运算法则是解题关键.
9.如果 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,那么 SKIPIF 1 < 0 = .
【答案】45
【分析】分别根据幂的乘方以及同底数幂的乘法法则解答即可.
【详解】解:∵ SKIPIF 1 < 0 , SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 .
故答案为:45.
【点睛】本题主要考查了同底数幂的乘法以及幂的乘方与积的乘方,熟记幂的运算法则是解答本题的关键.
三.比较幂的大小(共2题)
10.比较 SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 的大小正确的是( )
【答案】B
【分析】把三个数化成指数相同的幂比较大小,底数大的幂大.
【详解】解: SKIPIF 1 < 0 ;
SKIPIF 1 < 0 ;
SKIPIF 1 < 0 ;
∵ SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 .
故选:B.
【点睛】本题考查了有理数的大小比较,幂的乘方与积的乘方,解题的关键是掌握幂的乘法与积的乘方.
11.比较大小: SKIPIF 1 < 0 SKIPIF 1 < 0 .(填“>”、“<”或“=”)
【答案】<
【分析】根据幂的乘方解决此题.
【详解】解: SKIPIF 1 < 0 , SKIPIF 1 < 0 .
∵ SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 .
∴ SKIPIF 1 < 0 .
故答案为:<.
【点睛】本题主要考查幂的乘方,熟练掌握幂的乘方是解决本题的关键.
四.零指数幂和负整数指数幂的意义(共3题)
12.若 SKIPIF 1 < 0 成立,则a的值为( )
【答案】B
【分析】利用零指数幂的运算法则解题即可.
【详解】解:∵ SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 ,
解得 SKIPIF 1 < 0 ,
故选:B.
【点睛】本题考查零指数幂的运算,掌握零指数幂的底数不能为零是解题的关键.
13.代数式 SKIPIF 1 < 0 可以表示的是( )
【答案】C
【分析】直接利用负整数指数米的幂的性质化简,结合倒数的定义得出答案.
【详解】解:∵ SKIPIF 1 < 0 ,
∴代数式 SKIPIF 1 < 0 可以表示2的倒数.
故选:C.
【点睛】此题主要考查了负整数指数幂的性质以及倒数的定义,正确掌握相关定义是解题关键.
14.若 SKIPIF 1 < 0 有意义,则x取值范围是( )
【答案】D
【分析】直接利用负整数指数幂的性质以及零指数幂的性质得出答案.
【详解】解:若 SKIPIF 1 < 0 有意义,
则 SKIPIF 1 < 0 且 SKIPIF 1 < 0 ,
解得: SKIPIF 1 < 0 且 SKIPIF 1 < 0 .
故选:D.
【点睛】此题主要考查了负整数指数幂的性质以及零指数幂的性质,正确把握相关定义是解题关键.
五.用科学记数法表示小于1的数(共3题)
15.KN95型口罩能过滤空气中95%的粒径约为0.00000025m的非油性颗粒,用科学记数法表示0.00000025
是( )
【答案】D
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为 SKIPIF 1 < 0 ,与较大数的科学记数法不同的是其所使用的是负整数指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【详解】解:0.00000025= SKIPIF 1 < 0 .
故选:D.
【点睛】本题考查用科学记数法表示较小的数,一般形式为 SKIPIF 1 < 0 ,其中 SKIPIF 1 < 0 ,n为由原数左边起
第一个不为零的数字前面的0的个数所决定.
16.信息技术发展的今天,芯片制造的核心是光刻技术,我国的光刻技术水平已突破到28nm,已知
SKIPIF 1 < 0 ,则28nm用科学记数法表示是( )
【答案】A
【分析】科学记数法的表示形式为 SKIPIF 1 < 0 的形式,其中 SKIPIF 1 < 0 ,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
【详解】解:因为 SKIPIF 1 < 0 ,
所以 SKIPIF 1 < 0 .
故选:A.
【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为 SKIPIF 1 < 0 的形式,其中 SKIPIF 1 < 0 ,n
为整数,表示时关键要确定a的值以及n的值.
17.若把数字0.0000000618用科学记数法表示为 SKIPIF 1 < 0 的形式,则n= .
【答案】 SKIPIF 1 < 0
【分析】科学记数法的表示形式为 SKIPIF 1 < 0 的形式,其中 SKIPIF 1 < 0 ,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
【详解】解:0.0000000618= SKIPIF 1 < 0 .
∴ SKIPIF 1 < 0 .
故答案为: SKIPIF 1 < 0 .
【点睛】此题主要考查了用科学记数法表示较小的数,一般形式为 SKIPIF 1 < 0 ,其中 SKIPIF 1 < 0 ,n为由原数左边起第一个不为零的数字前面的0的个数所决定.
六.幂的综合运算(共5小题)
18.下列运算:
① SKIPIF 1 < 0 ;② SKIPIF 1 < 0 ;③ SKIPIF 1 < 0 ;④ SKIPIF 1 < 0 ;⑤ SKIPIF 1 < 0 .
其中错误的是 .(填写序号)
【答案】①②③⑤
【分析】利用同底数幂的除法的法则,同底数幂的乘法的法则,幂的乘方与积的乘方的法则对各式进行运算即可.
【详解】解:① SKIPIF 1 < 0 ,故①符合题意;
② SKIPIF 1 < 0 ,故②符合题意;
③ SKIPIF 1 < 0 ,故③符合题意;
④ SKIPIF 1 < 0 ,故④不符合题意;
⑤ SKIPIF 1 < 0 ,故⑤符合题意;
则错误的有①②③⑤.
故答案为:①②③⑤.
【点睛】本题主要考查同底数幂的除法,同底数幂的乘法,积的乘方,解答的关键是对相应的运算法则的掌握.
19.计算: SKIPIF 1 < 0 = .
【答案】1
【分析】根据负整数指数幂和零指数幂运算法则,以及乘方运算法则进行计算即可.
【详解】解: SKIPIF 1 < 0 .
【点睛】本题主要考查负整数指数幂,解题的关键是熟练掌握负整数指数幂和零指数幂运算法则,以及乘方运算法则,准确计算.
20.计算: SKIPIF 1 < 0 .
【答案】0
【分析】根据同底数幂的乘除法法则解答即可.
【详解】解: SKIPIF 1 < 0 .
【点睛】此题考查了同底数幂的乘除法,熟练掌握同底数幂的乘除法法则是解题的关键.
21.计算:
(1) SKIPIF 1 < 0 ;(2) SKIPIF 1 < 0 .
【答案】(1) SKIPIF 1 < 0 ;(2)0
【分析】(1)先算同底数幂的除法,再算同底数幂的乘法即可;
(2)先算积的乘方,同底数幂的乘法,再算同底数幂的除法,最后合并同类项即可.
【详解】解:(1) SKIPIF 1 < 0 ;
(2) SKIPIF 1 < 0 .
【点睛】本题主要考查同底数的除法,同底数幂的乘法,积的乘方,解答的关键是对相应的运算法则的掌握.
22.(1)若 SKIPIF 1 < 0 ,求m的值;
(2)已知 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,求 SKIPIF 1 < 0 的值;
(3)若n为正整数,且 SKIPIF 1 < 0 ,求 SKIPIF 1 < 0 的值.
【答案】(1)15;(2) SKIPIF 1 < 0 ;(3)80
【分析】(1)把代数式化为同底数幂的除法,再进行计算即可;
(2)先求出 SKIPIF 1 < 0 与 SKIPIF 1 < 0 的值,再进行计算即可;
(3)先把题中 SKIPIF 1 < 0 化为 SKIPIF 1 < 0 ,再把 SKIPIF 1 < 0 代入进行计算即可.
【详解】解:(1)∵ SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 ,解得 SKIPIF 1 < 0 ;
(2)∵ SKIPIF 1 < 0 , SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 , SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 ;
(3)∵ SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 .
【点睛】本题考查的是同底数幂的除法及幂的乘方与积的乘方法则,熟知以上知识是解题的关键.
七.运用整式乘法进行计算(共4小题)
23.计算:
(1) SKIPIF 1 < 0 ;(2) SKIPIF 1 < 0 .
【答案】(1) SKIPIF 1 < 0 (2) SKIPIF 1 < 0
【分析】(1)先利用单项式乘多项式法则计算,再合并同类项;
(2)利用多项式乘多项式法则计算.
【详解】解:(1) SKIPIF 1 < 0 ;
(2) SKIPIF 1 < 0 .
【点睛】本题考查了整式的混合运算,掌握单项式乘多项式、多项式乘多项式法则是解决本题的关键.
24.计算:
(1) SKIPIF 1 < 0 ;(2) SKIPIF 1 < 0 .
【答案】(1) SKIPIF 1 < 0 (2) SKIPIF 1 < 0
【分析】(1)先算积的乘方,再算单项式乘单项式;
(2)根据单项式乘多项式的计算法则计算即可求解.
【详解】解:(1) SKIPIF 1 < 0 ;
(2) SKIPIF 1 < 0 .
【点睛】本题考查了积的乘方,单项式乘单项式,单项式乘多项式,关键是熟练掌握计算法则正确进行计算.
25.计算: SKIPIF 1 < 0 .
【答案】 SKIPIF 1 < 0
【分析】根据单项式乘多项式的运算法则解答即可.
【详解】解: SKIPIF 1 < 0 .
【点睛】此题考查了单项式乘多项式,熟练掌握单项式乘多项式的运算法则:m(a+b+c)=ma+mb+mc是解题的关键.
26.先化简,再求值: SKIPIF 1 < 0 ,其中 SKIPIF 1 < 0 .
【答案】-98
【分析】首先根据单项式与多项式相乘的法则去掉括号,然后合并同类项,最后代入已知的数值计算即可.
【详解】解: SKIPIF 1 < 0 ,
当 SKIPIF 1 < 0 时,原式 SKIPIF 1 < 0 .
【点睛】本题考查了整式的化简.整式的加减运算实际上就是去括号、合并同类项,这是各地中考的常考点.
八.运用整式乘法确定字母的值(共3小题)
27.若 SKIPIF 1 < 0 ,则a= .
【答案】 SKIPIF 1 < 0
【分析】把 SKIPIF 1 < 0 化为 SKIPIF 1 < 0 ,根据等式的恒等性得出 SKIPIF 1 < 0 ,进而求出a的值.
【详解】解:∵ SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 ,
故答案为: SKIPIF 1 < 0 .
【点睛】本题考查多项式乘多项式的运算,掌握多项式乘多项式的运算法则,等式的恒等性是解题关键.
28.若 SKIPIF 1 < 0 与 SKIPIF 1 < 0 的乘积中不含x的二次项,则实数m的值为 .
【答案】 SKIPIF 1 < 0
【分析】利用多项式与多项式相乘,展开后合并同类项,再令含x的二次项系数为0,求解即可.
【详解】解: SKIPIF 1 < 0 ,
∵ SKIPIF 1 < 0 与 SKIPIF 1 < 0 的乘积中不含x的二次项,
∴ SKIPIF 1 < 0 ,
解得: SKIPIF 1 < 0 ,
∴实数m的值为 SKIPIF 1 < 0 .
故答案为: SKIPIF 1 < 0 .
【点睛】本题考查了多项式与多项式的乘积,掌握多项式与多项式的乘法法则与合并同类项是关键.
29.已知代数式 SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 .
(1)化简 SKIPIF 1 < 0 所表示的代数式;
(2)若代数式 SKIPIF 1 < 0 值与x的取值无关,求出a、b的值.
【答案】(1) SKIPIF 1 < 0 ;(2) SKIPIF 1 < 0 , SKIPIF 1 < 0
【分析】(1)把 SKIPIF 1 < 0 , SKIPIF 1 < 0 代入 SKIPIF 1 < 0 ,去括号,合并同类项计算即可;
(2)计算 SKIPIF 1 < 0 ,根据代数式 SKIPIF 1 < 0 值与x的取值无关列出方程解答即可.
【详解】解:(1)∵ SKIPIF 1 < 0 , SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0
= SKIPIF 1 < 0
= SKIPIF 1 < 0 ;
(2) SKIPIF 1 < 0
= SKIPIF 1 < 0
= SKIPIF 1 < 0
= SKIPIF 1 < 0 .
∵代数式 SKIPIF 1 < 0 的值与x的取值无关,
∴ SKIPIF 1 < 0 , SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 , SKIPIF 1 < 0 .
【点睛】本题考查了整式的混合运算,解题的关键是掌握单项式乘多项式以及整式加减的运算法则.
九.运用整式乘法解决实际问题(共3小题)
30.图1是长为a,宽为b(a>b)的小长方形纸片,将6张如图1的纸片按图2的方式不重叠地放在长方
形 SKIPIF 1 < 0 内,已知 SKIPIF 1 < 0 的长度固定不变,BC的长度可以变化,图中阴影部分(即两个长方形的面积分别表
示为 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,若 SKIPIF 1 < 0 ,且S为定值,则a,b满足的数量关系: .
【答案】 SKIPIF 1 < 0
【分析】设 SKIPIF 1 < 0 ,表示出 SKIPIF 1 < 0 和 SKIPIF 1 < 0 ,进一步可得 SKIPIF 1 < 0 ,根据S为定值,可得 SKIPIF 1 < 0 ,进一步可得a,b满足的数量关系
【详解】解:设 SKIPIF 1 < 0 ,
根据题意,得 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 ,
∵S为定值,
∴ SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 ,
故答案为: SKIPIF 1 < 0 .
【点睛】本题考查了多项式乘多项式,根据题意表示出 SKIPIF 1 < 0 是解题的关键.
31.甲、乙两个长方形的边长如图所示,其面积分别记为 SKIPIF 1 < 0 , SKIPIF 1 < 0 .
(1)请通过计算比较 SKIPIF 1 < 0 与 SKIPIF 1 < 0 的大小;
(2)若一个正方形的周长等于甲、乙两个长方形的周长的和,设该正方形的面积为 SKIPIF 1 < 0 ,试说明代数式 SKIPIF 1 < 0 的值是一个常数.
【答案】(1) SKIPIF 1 < 0 ;(2)20
【分析】(1)依据长方形面积公式,分别计算出 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,然后进行作差比较计算出 SKIPIF 1 < 0 即可判断;
(2)依据题意计算出正方形的周长,从而求出 SKIPIF 1 < 0 及 SKIPIF 1 < 0 即可.
【详解】解:(1) SKIPIF 1 < 0 , SKIPIF 1 < 0 ,
∵ SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 ;
(2)由题意得:正方形的边长是: SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 ,
∵ SKIPIF 1 < 0 ,
∴代数式 SKIPIF 1 < 0 的值是一个常数20.
【点睛】本题考查了整式的四则混合运算;解题的关键是理解题意,正确列式计算.
32.如图,某小区有一块长为 SKIPIF 1 < 0 米,宽为 SKIPIF 1 < 0 米的长方形地块,物业公司计划在小区内修一
条平行四边形小路,小路的底边宽为a米,将阴影部分进行绿化.
(1)用含有a、b的式子表示绿化的总面积S;
(2)若 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,求出此时绿化的总面积S.
【答案】(1) SKIPIF 1 < 0 平方米;(2)196平方米
【分析】(1)利用长方形的面积公式及平行四边形的面积公式进行求解即可;
(2)把相应的值代入(1)中运算即可.
【详解】解:(1)由题意得:
SKIPIF 1 < 0 平方米;
(2)当 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,
SKIPIF 1 < 0 (平方米).
【点睛】本题主要考查多项式乘多项式,解答的关键是对相应的运算法则的掌握.
十.两个乘法公式的基本运用(共7小题)
33.已知 SKIPIF 1 < 0 是完全平方式,则m的值为 .
【答案】 SKIPIF 1 < 0
【分析】利用完全平方公式得到 SKIPIF 1 < 0 ,从而得到 SKIPIF 1 < 0 ,从而求出m值.
【详解】解:∵ SKIPIF 1 < 0 是完全平方式,
∴ SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 ,
故答案为: SKIPIF 1 < 0 .
【点睛】本题考查了完全平方式,解题的关键是熟练掌握完全平方公式.
34.多项式 SKIPIF 1 < 0 是一个完全平方式,则k= .如果 SKIPIF 1 < 0 是完全平方式,则m的值
是 .
【答案】16, SKIPIF 1 < 0
【分析】利用完全平方公式的结构特征判断即可得解.
【详解】解:∵多项式 SKIPIF 1 < 0 是一个完全平方式,
∴ SKIPIF 1 < 0 ,
∵ SKIPIF 1 < 0 是完全平方式,
∴ SKIPIF 1 < 0 ,即 SKIPIF 1 < 0 ,
又∵ SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 .
故答案为:16, SKIPIF 1 < 0 .
【点睛】此题考查了完全平方式,熟练掌握完全平方公式是解本题的关键.
35.已知正方形的周长是 SKIPIF 1 < 0 cm,则其面积是 cm2.
【答案】 SKIPIF 1 < 0
【分析】先求得该正方形的边长,再运用完全平方公式进行求解.
【详解】解:∵该正方形的边长为:
SKIPIF 1 < 0 (cm),
∴该正方形的面积为:
SKIPIF 1 < 0 (cm2),
故答案为: SKIPIF 1 < 0 .
【点睛】此题考查了完全平方公式的应用能力,关键是能准确理解并运用该知识.
36. SKIPIF 1 < 0 = .
【答案】9
【分析】原式变形后,利用完全平方公式化简,计算即可求出值.
【详解】解:原式= SKIPIF 1 < 0
= SKIPIF 1 < 0
= SKIPIF 1 < 0
=9.
故答案为:9.
【点睛】此题考查了完全平方公式,熟练掌握完全平方公式是解本题的关键.
37.运用乘法公式简便计算: SKIPIF 1 < 0 = .
【答案】1
【分析】将数字适当变形后,利用平方差公式解答即可.
【详解】解:原式= SKIPIF 1 < 0
= SKIPIF 1 < 0
= SKIPIF 1 < 0
=1.
故答案为:1.
【点睛】本题主要考查了实数的运算,平方差公式,熟练掌握平方差公式是解题的关键.
38.化简: SKIPIF 1 < 0 .
【答案】 SKIPIF 1 < 0
【分析】根据完全平方公式先把原式进行化简,再合并即可.
【详解】解: SKIPIF 1 < 0
= SKIPIF 1 < 0
= SKIPIF 1 < 0 .
【点睛】本题考查了整式的混合运算,涉及的知识有:完全平方公式以及合并同类项法则,熟练掌握公式及法则是解本题的关键.
39.阅读材料后解决问题.小明遇到下面一个问题:
计算 SKIPIF 1 < 0 .
经过观察,小明发现如果将原式进行适当的变形后可以出现特殊的结构,进而可以应用平方差公式解决问题,具体解法如下:
SKIPIF 1 < 0
= SKIPIF 1 < 0
= SKIPIF 1 < 0
= SKIPIF 1 < 0
= SKIPIF 1 < 0
= SKIPIF 1 < 0 .
请你根据小明解决问题的方法,试着解决以下的问题:
(1) SKIPIF 1 < 0 ;
(2) SKIPIF 1 < 0 .
【答案】(1) SKIPIF 1 < 0 ;(2) SKIPIF 1 < 0
【分析】(1)根据题中例题可得,在本题式子前面可乘以 SKIPIF 1 < 0 ,然后利用平方差公式即可算出答案;
(2)根据题中例题可得,在整体的式子前面乘以 SKIPIF 1 < 0 ,要想保持结果不变,再在式子前面乘以 SKIPIF 1 < 0 ,然后利用平方差公式即可运算.
【详解】解:(1)原式= SKIPIF 1 < 0
= SKIPIF 1 < 0
= SKIPIF 1 < 0
= SKIPIF 1 < 0
= SKIPIF 1 < 0
= SKIPIF 1 < 0 ;
(2)原式= SKIPIF 1 < 0
= SKIPIF 1 < 0
= SKIPIF 1 < 0
= SKIPIF 1 < 0
= SKIPIF 1 < 0
= SKIPIF 1 < 0 .
【点睛】本题考查的是平方差公式的应用,解题关键是掌握平方差公式.
十一.两个乘法公式的推广及综合运用(共7小题)
40.如图,将图1的长方形用剪刀沿图中虚线(对称轴)剪开,分成四块形状和大小一样的小长方形,小
长方形的长为a,宽为b(a>b),再按图2的方式拼成一个正方形,通过拼接前后两个图形中阴影部分的
面积关系可以验证的等式是( )
【答案】B
【分析】根据4个长方形的面积等于大正方形的面积减去小正方形的面积即可求解.
【详解】解:∵图1阴影的面积为: SKIPIF 1 < 0 ,
图2阴影的面积为: SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 ,
故选:B.
【点睛】本题考查了完全平方公式与几何图形,数形结合是解题的关键.
41.如图,对一个正方形进行了分割,通过面积恒等,能够验证下列哪个等式( )
【答案】C
【分析】观察图形的面积,从整体看怎么表示,再从分部分来看怎么表示,两者相等,即可得答案.
【详解】解:首先看四个等式都是成立的,但是却并未都正确反映图示内容.
图中大正方形的边长为: SKIPIF 1 < 0 ,其面积可以表示为: SKIPIF 1 < 0
分部分来看:左下角正方形面积为 SKIPIF 1 < 0 ,右上角正方形面积为 SKIPIF 1 < 0 ,
其余两个长方形的面积均为 SKIPIF 1 < 0 ,
各部分面积相加得: SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0
故选:C.
【点睛】本题考查了乘法公式的几何背景,明确几何图形面积的表达方式,熟练掌握相关乘法公式,是解
题的关键.
42.若 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 = .
【答案】28
【分析】先把 SKIPIF 1 < 0 变形为 SKIPIF 1 < 0 ,然后把 SKIPIF 1 < 0 , SKIPIF 1 < 0 代入计算即可.
【详解】解: SKIPIF 1 < 0 ,
当 SKIPIF 1 < 0 , SKIPIF 1 < 0 时,原式= SKIPIF 1 < 0 .
故答案为:28.
【点睛】题考查了完全平方公式,掌握 SKIPIF 1 < 0 是解题的关键.
43.已知 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 = .
【答案】16
【分析】将 SKIPIF 1 < 0 变形为 SKIPIF 1 < 0 ,然后将 SKIPIF 1 < 0 , SKIPIF 1 < 0 代入求解即可.
【详解】.解:∵ SKIPIF 1 < 0 , SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 .
故答案为:16.
【点睛】本题主要考查了完全平方公式,掌握完全平方公式进行运算是关键.
44.已知: SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 = .
【答案】7
【分析】根据完全平方公式解答即可.
【详解】解:∵ SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 ,
故答案为:7.
【点睛】本题考查了完全平方公式,熟记完全平方公式是解题的关键.
45.计算: SKIPIF 1 < 0 = .
【答案】 SKIPIF 1 < 0
【分析】原式利用完全平方公式展开即可得到结果.
【详解】解:原式= SKIPIF 1 < 0 .
故答案为: SKIPIF 1 < 0 .
【点睛】此题考查了完全平方公式,熟练掌握公式是解本题的关键.
46.用如图所示的正方形和长方形卡片若干张,拼成一个边长为 SKIPIF 1 < 0 的正方形,需要B类卡片 张.
【答案】6
【分析】根据题意列出关系式,利用完全平方公式化简即可作出判断.
【解答】解:根据题意得: SKIPIF 1 < 0 ,
则需要B类卡片6张.
故答案为:6.
【点评】此题考查了完全平方式,熟练掌握完全平方公式是解本题的关键.
十二.整式的混合运算(共3小题)
47.计算:
(1) SKIPIF 1 < 0 ;(2) SKIPIF 1 < 0 .
【答案】(1) SKIPIF 1 < 0 ;(2) SKIPIF 1 < 0
【分析】(1)先去括号再合并同类项即可;
(2)按照完全平方和公式和多项式除以单项式法则去括号,然后合并同类项即可.
【详解】解:(1)原式= SKIPIF 1 < 0 ;
(2)原式= SKIPIF 1 < 0
= SKIPIF 1 < 0
= SKIPIF 1 < 0 .
【点睛】本题考查了整式的计算,掌握完全平方和公式和相关运算法则是关键.
48.计算:
(1) SKIPIF 1 < 0 ;(2) SKIPIF 1 < 0 .
【答案】(1) SKIPIF 1 < 0 ;(2) SKIPIF 1 < 0
【分析】(1)根据整式的乘除运算法则即可求出答案.
(2)根据完全平方公式以及多项式乘多项式法则即可求出答案.
【详解】解:(1)原式= SKIPIF 1 < 0
= SKIPIF 1 < 0
= SKIPIF 1 < 0 .
(2)原式= SKIPIF 1 < 0
= SKIPIF 1 < 0
= SKIPIF 1 < 0 .
【点睛】本题考查整式的混合运算,解题的关键是熟练运用整式的加减运算法则以及乘除运算法则,本题属于基础题型.
49.规定一种新运算法则: SKIPIF 1 < 0 .
(1)求 SKIPIF 1 < 0 的值;
(2)若 SKIPIF 1 < 0 ,求 SKIPIF 1 < 0 的值.
【答案】(1)3;(2)21
【分析】(1)根据新定义的运算代入求解即可;
(2)根据新定义的运算得出 SKIPIF 1 < 0 ,然后代入求解即可.
【详解】解:(1)由题意得:
SKIPIF 1 < 0
= SKIPIF 1 < 0
= SKIPIF 1 < 0
=3;
(2)由题意得: SKIPIF 1 < 0 ,
解得: SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0
= SKIPIF 1 < 0
= SKIPIF 1 < 0
=21.
【点睛】本题主要考查整式的混合运算,理解新定义的运算,熟练掌握运算法则是解题关键.
十三.整式乘除的实际运用(共1小题)
50.如图,两个形状大小相同的长方形 SKIPIF 1 < 0 和长方形 SKIPIF 1 < 0 ,点E在 SKIPIF 1 < 0 边上, SKIPIF 1 < 0 , SKIPIF 1 < 0 ,
且a>b>0.
(1)用含a,b的代数式分别表示 SKIPIF 1 < 0 和 SKIPIF 1 < 0 的面积;
(2)当 SKIPIF 1 < 0 , SKIPIF 1 < 0 .求图中阴影部分的面积.
【答案】(1) SKIPIF 1 < 0 的面积为 SKIPIF 1 < 0 , SKIPIF 1 < 0 的面积为 SKIPIF 1 < 0 ;(2)20
【分析】(1)根据已知易得 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,从而可得 SKIPIF 1 < 0 ,然后利用三角形的面积公式,进行计算即可解答;
(2)根据阴影部分的面积=梯形 SKIPIF 1 < 0 的面积﹣ SKIPIF 1 < 0 的面积﹣ SKIPIF 1 < 0 的面积,再利用(1)的结论,进行计算即可解答.
【详解】解:(1)∵长方形 SKIPIF 1 < 0 和长方形 SKIPIF 1 < 0 是两个形状大小相同的长方形,
∴ SKIPIF 1 < 0 , SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 的面积= SKIPIF 1 < 0 ;
SKIPIF 1 < 0 的面积= SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 的面积为 SKIPIF 1 < 0 , SKIPIF 1 < 0 的面积为 SKIPIF 1 < 0 ;
(2)∵ SKIPIF 1 < 0 , SKIPIF 1 < 0 ,
∴阴影部分的面积=梯形 SKIPIF 1 < 0 的面积﹣ SKIPIF 1 < 0 的面积﹣ SKIPIF 1 < 0 的面积
= SKIPIF 1 < 0
= SKIPIF 1 < 0
= SKIPIF 1 < 0
= SKIPIF 1 < 0
= SKIPIF 1 < 0
= SKIPIF 1 < 0
= SKIPIF 1 < 0
=20,
∴图中阴影部分的面积为20.
【点睛】本题考查了整式的混合运算,完全平方公式的几何背景,准确熟练地进行计算是解题的关键.A. SKIPIF 1 < 0
B. SKIPIF 1 < 0
C. SKIPIF 1 < 0
D. SKIPIF 1 < 0
A. SKIPIF 1 < 0
B. SKIPIF 1 < 0
C. SKIPIF 1 < 0
D. SKIPIF 1 < 0
A. SKIPIF 1 < 0
B. SKIPIF 1 < 0
C. SKIPIF 1 < 0
D. SKIPIF 1 < 0
A. SKIPIF 1 < 0
B. SKIPIF 1 < 0
C. SKIPIF 1 < 0
D. SKIPIF 1 < 0
A. SKIPIF 1 < 0
B. SKIPIF 1 < 0
C. SKIPIF 1 < 0
D. SKIPIF 1 < 0
A. SKIPIF 1 < 0
B. SKIPIF 1 < 0
C. SKIPIF 1 < 0
D. SKIPIF 1 < 0 或 SKIPIF 1 < 0
A.2的相反数
B.2的绝对值
C.2的倒数
D.2与1的差
A. SKIPIF 1 < 0
B. SKIPIF 1 < 0
C. SKIPIF 1 < 0 且 SKIPIF 1 < 0
D. SKIPIF 1 < 0 且 SKIPIF 1 < 0
A. SKIPIF 1 < 0
B. SKIPIF 1 < 0
C. SKIPIF 1 < 0
D. SKIPIF 1 < 0
A. SKIPIF 1 < 0
B. SKIPIF 1 < 0
C. SKIPIF 1 < 0
D. SKIPIF 1 < 0
A. SKIPIF 1 < 0
B. SKIPIF 1 < 0
C. SKIPIF 1 < 0
D. SKIPIF 1 < 0
A. SKIPIF 1 < 0
B. SKIPIF 1 < 0
C. SKIPIF 1 < 0
D. SKIPIF 1 < 0
北师大版数学七年级下册期末复习考点串讲+题型专训专题11 概率初步(2份打包,原卷版+含解析): 这是一份北师大版数学七年级下册期末复习考点串讲+题型专训专题11 概率初步(2份打包,原卷版+含解析),文件包含部编七年级上册语文第五单元教材知识点考点梳理pptx、部编七年级上册语文第五单元教材知识点考点梳理教案docx、部编七年级上册语文第五单元教材知识点考点梳理验收卷原卷版docx、部编七年级上册语文第五单元教材知识点考点梳理验收卷解析版docx等4份课件配套教学资源,其中PPT共31页, 欢迎下载使用。
北师大版数学七年级下册期末复习考点串讲+题型专训专题10 生活中的轴对称(2份打包,原卷版+含解析): 这是一份北师大版数学七年级下册期末复习考点串讲+题型专训专题10 生活中的轴对称(2份打包,原卷版+含解析),文件包含部编七年级上册语文第五单元教材知识点考点梳理pptx、部编七年级上册语文第五单元教材知识点考点梳理教案docx、部编七年级上册语文第五单元教材知识点考点梳理验收卷原卷版docx、部编七年级上册语文第五单元教材知识点考点梳理验收卷解析版docx等4份课件配套教学资源,其中PPT共31页, 欢迎下载使用。
北师大版数学七年级下册期末复习考点串讲+题型专训专题04 三角形(2份打包,原卷版+含解析): 这是一份北师大版数学七年级下册期末复习考点串讲+题型专训专题04 三角形(2份打包,原卷版+含解析),文件包含部编七年级上册语文第五单元教材知识点考点梳理pptx、部编七年级上册语文第五单元教材知识点考点梳理教案docx、部编七年级上册语文第五单元教材知识点考点梳理验收卷原卷版docx、部编七年级上册语文第五单元教材知识点考点梳理验收卷解析版docx等4份课件配套教学资源,其中PPT共31页, 欢迎下载使用。












