【期中真题】广西玉林市2022届高三上学期教学质量监测数学（理）试题.zip

2021年11月份玉林市高三教学质量监测试题数学（理科）

一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1. 已知是虚数单位，是复数，若，则复数的虚部为（    ）

A.  B.

C.  D.

【答案】B

【解析】

【分析】

由可化为，根据复数的除法计算即可求解.

【详解】由，

得，

所以虚部为，

故选：B

【点睛】本题主要考查了复数的除法运算，考查了复数的概念，属于容易题.

2. 设集合，，且，则实数的取值集合为（    ）

A.  B.  C.  D.

【答案】A

【解析】

【分析】化简集合，进一步得出答案.

【详解】由题得，

因为，且，

所以实数的取值集合为.

故选：A.

3. 下列函数中是减函数且值域为R的是（    ）

A  B.  C.  D.

【答案】D

【解析】

【分析】由幂函数及对数函数的图象与性质即可求解.

【详解】解：对A：函数的值域为，故选项A错误；

对B：函数为和上的增函数，故选项B错误；

对C：函数，所以在上单调递增，在上单调递减，故选项C错误；

对D：由幂函数的性质知为减函数且值域为R，故选项D正确；

故选：D.

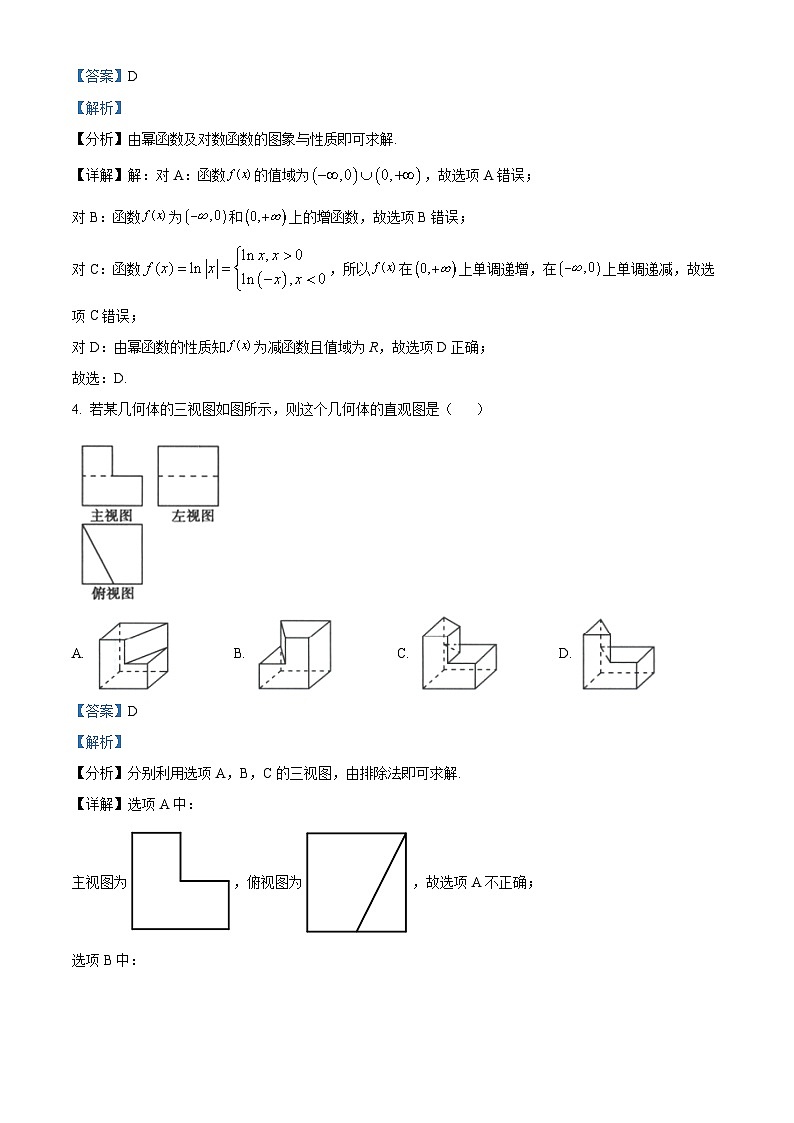
4. 若某几何体的三视图如图所示，则这个几何体的直观图是（    ）

A.  B.  C.  D.

【答案】D

【解析】

【分析】分别利用选项A，B，C的三视图，由排除法即可求解.

【详解】选项A中：

主视图为，俯视图为，故选项A不正确；

选项B中：

主视图为，侧视图为，故选项B不符合题意；

选项C中：

俯视图为，故选项C不符合题意，

故选：D.

5. 的展开式中，的系数为（    ）

A. 11 B.  C. 30 D.

【答案】D

【解析】

【分析】先求得的展开式的通项公式，再由求解.

【详解】因为的展开式的通项公式为，

且，

所以的展开式中的系数为，

故选：D.

6. 如图，一架飞机从A地飞往B地，两地相距500km.飞行员为了避开某一区域的雷雨云层，从A点起飞以后，就沿与原来的飞行方向AB成角的方向飞行，飞行到中途C点，再沿与原来的飞行方向AB成角的方向继续飞行到终点B点.这样飞机的飞行路程比原来的路程500km大约多飞了（ ）（，）

A. 10km B. 20km

C. 30km D. 40km

【答案】B

【解析】

【分析】由题得，再由正弦定理求出，即得解.

【详解】在中，由，得，

由正弦定理得，

所以，

所以，

所以，

故选：B.

7. 已知向量，为非零向量，则“向量，的夹角为180°”是“”的（    ）

A. 充分不必要条件 B. 必要不充分条件

C. 充要条件 D. 既不充分也不必要条件

【答案】A

【解析】

【分析】判断命题“若向量，的夹角为180°，则”和命题“若，则向量，的夹角为180°”的真假即可得解.

【详解】因向量，为非零向量，则当向量，的夹角为180°时，与方向相反，即成立，

当时，与方向相同或者方向相反，即向量，的夹角为0°或者180°，可以不为180°，

所以“向量，的夹角为180°”是“”的充分不必要条件.

故选：A

8. 已知点是抛物线的对称轴与准线的交点，点为该抛物线的焦点，抛物线上纵坐标为1的点P满足，则（    ）

A.  B. 4 C.  D. 2

【答案】C

【解析】

【分析】借助抛物线定义和两点间距离公式求解即可．

【详解】由题意，，点，故，，

．

故选：C．

9. 已知数列为等比数列，若，且与的等差中项为，则的最大值为（    ）

A. 5 B. 512 C. 1024 D. 2048

【答案】C

【解析】

【分析】

用和表示出和代入求得，再根据，求得，进而求得到的值，即得解.

【详解】

，

故，

所以，

所以数列的前4或5项的积最大，且最大值为.

故选：C

【点睛】结论点睛：等比数列中，如果，求的最大值，一般利用“1交界”法求解，即找到大于等于1的项，找到小于1的项，即得解.

10. 已知，且，则（    ）

A.  B.

C.  D.

【答案】B

【解析】

【分析】利用同角公式化正弦为余弦，求出的值，再利用二倍角的余弦公式求解即得.

【详解】依题意，原等式化为：，整理得：，

因，则，解得：，

所以.

故选：B

11. 如图所示三棱锥中，∠BCD=90°，△ABD为等边三角形，二面角为直二面角，，则该三棱锥外接球体积为（    ）

A.  B.  C.  D.

【答案】B

【解析】

【分析】根据几何关系，找到球心在的外心处，利用正弦定理求得三角形外接圆半径，再求球体的体积即可.

【详解】取BD中点E，连接AE，如下图所示：

在等边中，；

又二面角为直二面角，

故平面平面CBD，又面面，面,

所以平面BCD.

因为为以为斜边的直角三角形，所以是的外心，

所以三棱锥的外接球的球心在线段上，且为的外心，设为.

设球的半径为，在中，由正弦定理有，解得.

所以体积为.

故选：B.

【点睛】关键点点睛：本题考察三棱锥外接球球半径的求解；本题中，球心是底面外心的垂线和侧面外心垂线的交点，这是处理问题的关键，属中档题.

12. 设，，．则（    ）

A.  B.  C.  D.

【答案】B

【解析】

【分析】利用对数的运算和对数函数的单调性不难对a,b的大小作出判定，对于a与c，b与c的大小关系，将0.01换成x,分别构造函数,，利用导数分析其在0的右侧包括0.01的较小范围内的单调性，结合f(0)=0,g(0)=0即可得出a与c，b与c的大小关系.

详解】[方法一]：

，

所以；

下面比较与的大小关系.

记，则，，

由于

所以当0<x<2时，，即，，

所以在上单调递增，

所以，即，即；

令，则，，

由于，在x>0时，，

所以，即函数在[0，+∞)上单调递减，所以，即，即b<c；

综上，，

故选：B.

[方法二]：

令

，即函数在（1，+∞)上单调递减

令

，即函数在（1，3)上单调递增

综上，，

故选：B.

【点睛】本题考查比较大小问题，难度较大，关键难点是将各个值中共同的量用变量替换，构造函数，利用导数研究相应函数的单调性，进而比较大小，这样的问题，凭借近似估计计算往往是无法解决的.

二、填空题：本题共4小题，每小题5分，共20分.

13. 若是函数的一个极值点，则______．

【答案】

【解析】

【分析】由是函数的一个极值点得，利用求解.

【详解】由题知，，.

因为是函数的一个极值点，所以，

有，.

故答案为：.

14. 设Sn为数列{an}的前n项和，且a1=2，（n≥2），则S4=___________.

【答案】54

【解析】

【分析】利用分别求出即可求出S4.

【详解】根据题意，数列{an}中，（n≥2），则，，，所以S4=2+4+12+36=54.

故答案为：54.

15. 已知由一组样本数据确定的回归直线方程为，且，发现有两组数据与误差较大，去掉这两组数据后，重新求得回归直线的斜率为1，那么当时，y的估计值为________.

【答案】6

【解析】

【分析】

先根据，求出，再根据去掉的两组数据发现样本中心点没变，求出新的回归直线方程，将代入即可求得.

【详解】解：，

，

由题意知：去掉两组数据和后，样本中心点没变，

设重新求得的回归直线方程为，

将样本点的中心代入，

解得：，

即

当时，.

故答案为：.

16. 椭圆C：的上、下顶点分别为A，C，点B在椭圆上，平面四边形ABCD满足∠BAD=∠BCD=90°，且，则该椭圆的离心率为__________﹒

【答案】##

【解析】

【分析】根据已知条件知、、、在以为直径的圆上，设，，，，结合圆的性质以及所给面积关系可得，，求得圆的方程，代入点坐标经计算即可得解﹒

【详解】根据题意可得，，设，，由，可得点A、B、C、D在以DB为直径的圆上，

又原点О为圆上的弦AC的中点，∴圆心在AC的垂直平分线上，可得圆心在x轴上，∴，

又，可得，

故圆心坐标为，半径为，

∴圆的方程为，

将A代入结合，可得，∴，，，

故答案为：﹒

三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17～21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答.

（一）必考题：共60分.

17. 已知函数.

（1）若，求f（x）的单调递增区间；

（2）若f（x）在[0，m]上的最小值为2，求实数m的取值范围.

【答案】（1）（）   

（2）

【解析】

【分析】（1）先化简得到，利用复合函数单调性“同增异减”列不等式求出f（x）的递增区间；.

（2）利用单调性实数m的取值范围.

【小问1详解】

.

令，（）

解得，（）

∴f（x）的递增区间为（）.

【小问2详解】

，得.

∵f（x）在上的最小值为2，

∴，

解得.

18. 2019年4月，江苏省发布了高考综合改革实施方案，试行“”高考新模式.为调研新高考模式下，某校学生选择物理或历史与性别是否有关，统计了该校高三年级800名学生的选科情况，部分数据如下表：

（1）根据所给数据完成上述表格，并判断是否有99.9%的把握认为该校学生选择物理或历史与性别有关；

（2）该校为了提高选择历史科目学生的数学学习兴趣，用分层抽样的方法从该类学生中抽取5人，组成数学学习小组.一段时间后，从该小组中抽取2人汇报数学学习心得.求这2人均为男生的概率.

附：

【答案】（1）表格见解析，有；（2）.

【解析】

【分析】（1）根据题中所给的公式，结合表中的数据求解判断即可；

（2）根据分层抽样的性质，结合古典概型的计算公式用列举法进行求解即可.

【详解】（1）

因为，

所以有99.9%的把握认为该校学生选择物理或历史与性别有关.

（2）按照分层抽样的方法，抽取男生2人，女生3人.设2名男生和3名女生分别为：，

则所有抽取结果有共10种，

均为男生只有一种，所以概率为.

19. 在四棱锥P﹣ABCD中，底面四边形ABCD是一个菱形，且∠ABC，AB＝2，PA⊥平面ABCD．

（1）若Q是线段PC上的任意一点，证明：平面PAC⊥平面QBD．

（2）当平面PBC与平面PDC所成的锐二面角的余弦值为时，求PA的长．

【答案】（1）见解析（2）

【解析】

【分析】（1）先证明BD⊥平面PAC，再由面面垂直的判定定理即可得证；

（2）建立空间直角坐标系，设P(0,1,a)（a>0），求出平面PBC与平面PDC的法向量，利用向量夹角公式建立关于a的方程，解出即可．

【详解】（1）证明：∵四边形ABCD是一个菱形，∴AC⊥BD，

又PA⊥平面ABCD，∴PA⊥BD，

又AC∩PA=A，则BD⊥平面PAC，

∵BD在平面QBD内，

∴平面PAC⊥平面QBD；

（2）设AC，BD交于点O，分别以OB，OC所在直线为x轴，y轴，以平行于AP的直线为z轴建立如图所示的空间直角坐标系，

则，设P(0,1，a)(a>0)，

则，

设平面PBC的一个法向量为，

则，则，

同理可求平面PDC的一个法向量为，

∴，解得a2=2，

∴．

【点睛】本题考查了面面垂直的判定以及利用空间向量求解二面角问题，考查了计算能力，属于中档题．

20. 双曲线左右焦点分别为，，实轴长，点P为双曲线C右支上一点，且的最小值为．

（1）求双曲线C的标准方程：

（2）过点作直线l与双曲线C右支交于A，B两点，若，求直线l的方程．

【答案】（1）；（2）．

【解析】

【分析】（1）利用实轴长求得的值，结合平面向量数量积求得双曲线的标准方程；（2）设，和双曲线方程联立利用韦达定理结合平面向量线性运算求得结果．

【详解】（1），则

双曲线C方程是：

（2）设，，，，①

，②，③

由①②③得，此时检验得

∴直线l的方程：

21. 已知函数.

（1）若存在零点，求实数的取值范围；

（2）若是的零点，求证：.

【答案】（1）；   

（2）证明见解析.

【解析】

【分析】（1）分离参数得，构造函数利用导数研究其单调性和值域，结合题意，则问题得解；

（2）根据（1）中所求，将所证不等式转化证明，分别构造函数，利用导数研究函数单调性，进而证明不等式恒成立即可.

【小问1详解】

令变形得，

令，问题转化成与有交点.

令，解得，

则在上单调递增，在上单调递减，

且，

故，

所以.

故实数的取值范围；

【小问2详解】

证明：由题意可得，，得，

要证，即证.

.先证，只需让，

令，.

所以在上单调递减，在上单调递增，

故，所以，左边证毕.

再证，即证：

令，，

所以在上单调递增，在上单调递减，

故；

令，，

令，，令，解得，

故在单调递增，.

即在恒成立.

令，解得，

所以在上单调递减，在上单调递增，

故.

因为，所以，

即，故，右边证毕.

综上所述：.

【点睛】本题考察利用导数研究函数单调性和恒成立问题；其中第一问中，对函数进行分离参数是解决问题的关键；第二问中，在证明时，将其转化为证明，是较好的一种处理手段；本题综合考察学生的计算能力，对导数的综合使用能力，属压轴题.

（二）选考题：共10分.请考生在第22、23题中任选一题作答.如果多做，那么按所做的第一题计分.

选修4-4：坐标系与参数方程

22. 在直角坐标系中，圆的圆心坐标为，以坐标原点为极点，轴正半轴为极轴建立极坐标系，点的极坐标为，且过点只能作一条圆的切线．

（1）求圆的极坐标方程；

（2）直线（，）和圆相交于两点，，若，求．

【答案】（1）；（2）．

【解析】

【分析】（1）首先根据题意得到，从而得到圆的标准方程，再转化为极坐标方程即可.

（2）首先将代入圆的极坐标方程得，得到设点，的极坐标分别为，，根据题意得到，且，再求解即可.

【详解】（1）由点的极坐标可得其直角坐标为，

因为过点只能作一条圆的切线，

所以点在圆上，

因为，

所以圆的直角坐标方程为，即，

所以圆的极坐标方程为．

（2）将代入圆的极坐标方程得，

由，，即，

设点，的极坐标分别为，，

则

又由，可得，

联立解得．

选修4-5：不等式选讲

23. 设函数.

（1）若，，求的取值范围；

（2）若，证明：.

【答案】（1）；（2）证明见解析.

【解析】

【分析】（1）根据，把不等式中的进行消元，然后分类讨论进行求解即可；

（2）利用重要不等式，结合绝对值的性质进行证明即可.

详解】（1）当时，，由得，

当时，恒成立，此时；

当时，，，此时，

综上可得，.

（2）∵，∴，，

∴.

【点睛】本题考查了利用分类讨论法求解绝对值不等式问题，考查了利用重要不等式和绝对值的性质进行证明不等式问题，考查了数学运算能力和推理论证能力.