




【期中真题】四川省成都市成都市石室中学2022-2023学年高三上学期期中数学理科试题.zip
展开成都石室中学2022-2023学年度上期高2023届11月半期考试
理科数学
一、选择题:本大题共12小题,每小题5分,共60分.在每小题列出的四个选项中,只有一项是符合题目要求的.
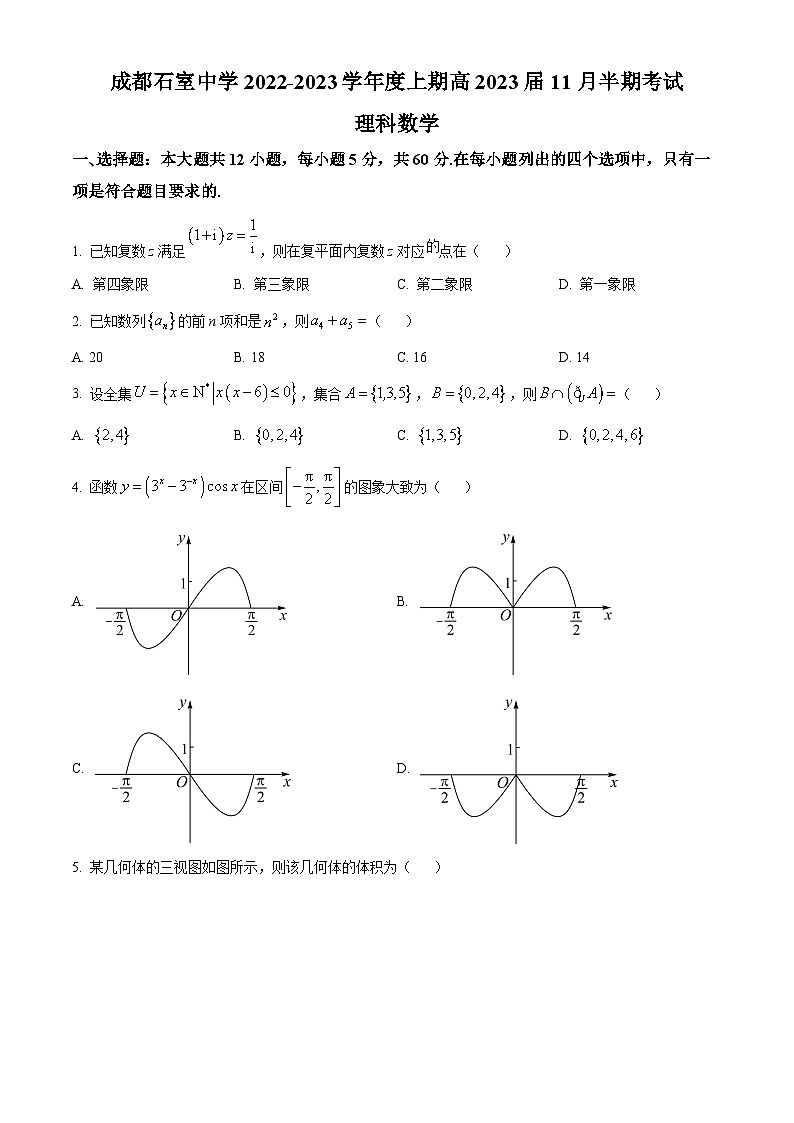
1. 已知复数z满足,则在复平面内复数z对应的点在( )
A. 第四象限 B. 第三象限 C. 第二象限 D. 第一象限
【答案】B
【解析】
【分析】结合复数的除法运算化简,由复数与复平面的对应关系即可求解.
【详解】因为,所以,
所以复数z对应的点为,故在复平面内复数z对应的点在第三象限.
故选:B.
2. 已知数列的前n项和是,则( )
A. 20 B. 18 C. 16 D. 14
【答案】C
【解析】
【分析】由直接代值运算即可.
【详解】设数列的前n项和为,则,故.
故选:C.
3. 设全集,集合,,则( )
A. B. C. D.
【答案】A
【解析】
【分析】解一元二次不等式进而确定全集中的元素,根据集合A,求得,根据集合的交集运算即可求得答案.
【详解】因为全集,
集合,所以,
又因为,所以,
故选:A.
4. 函数在区间的图象大致为( )
A. B.
C. D.
【答案】A
【解析】
【分析】由函数的奇偶性结合指数函数、三角函数的性质逐项排除即可得解.
【详解】令,
则,
所以为奇函数,排除BD;
又当时,,所以,排除C.
故选:A.
5. 某几何体的三视图如图所示,则该几何体的体积为( )
A. B. C. D.
【答案】A
【解析】
【分析】由三视图可还原几何体为一个正方体挖去一个圆锥,根据柱体和锥体的体积公式可求得结果.
【详解】由三视图可知几何体是一个棱长为的正方体挖去一个底面半径为,高为的圆锥,如图所示,
几何体体积.
故选:A.
6. 已知命题p:在中,若,则;命题q:向量与向量相等的充要条件是且.在下列四个命题中,是真命题的是( )
A. B. C. D.
【答案】D
【解析】
【分析】结合余弦三角函数单调性可判断正确,由向量相等的条件可判断错误.
【详解】命题p:在中,若,由于余弦函数在上单调递减,则,故命题p为真命题;
命题q:向量与向量相等的充要条件是向量与向量大小相等,方向相同,故命题q是假命题,
因此,为假命题,为假命题,为假命题,为真命题.
故选:D.
7. 已知函数的部分图象如图所示,则下列说法正确的是( )
A. 直线是函数的图象的一条对称轴
B. 函数的图象的对称中心为,
C. 函数在上单调递增
D. 将函数的图象向左平移个单位长度后,可得到一个偶函数的图象
【答案】B
【解析】
【分析】先根据函数图象,求出函数的解析式,然后根据三角函数的周期,对称轴,单调区间,奇偶性逐项进行检验即可求解.
【详解】由函数图象可知,,最小正周期为,所以.将点代入函数解析式中,得.又因为,所以,故.
对于A,令,,即,,令,则,故A错误;
对于B,令,则,,所以,,即函数图象的对称中心为,,故B正确;
对于C,令,解得,
因为,所以函数在上单调递减,
在上单调递增,故C错误;
对于D,将函数的图象向左平移个单位长度后,得到的图象,该函数不是偶函数,故D错误.
故选:.
8. 数列中,,对任意 ,若,则 ( )
A. 2 B. 3 C. 4 D. 5
【答案】C
【解析】
【分析】取,可得出数列是等比数列,求得数列的通项公式,利用等比数列求和公式可得出关于的等式,由可求得的值.
【详解】在等式中,令,可得,,
所以,数列是以为首项,以为公比的等比数列,则,
,
,则,解得.
故选:C.
【点睛】本题考查利用等比数列求和求参数的值,解答的关键就是求出数列的通项公式,考查计算能力,属于中等题.
9. 2020年,由新型冠状病毒(SARS-CoV-2)感染引起的新型冠状病毒肺炎(COVID-19)在国内和其他国家暴发流行,而实时荧光定量PCR(RT-PCR)法以其高灵敏度与强特异性,被认为是COVID-19的确诊方法,实时荧光定量PCR法,通过化学物质的荧光信号,对在PCR扩增进程中成指数级增加的靶标DNA实时监测,在PCR扩增的指数时期,荧光信号强度达到阈值时,DNA的数量与扩增次数n满足,其中p为扩增效率,为DNA的初始数量.已知某样本的扩增效率,则被测标本的DNA大约扩增( )次后,数量会变为原来的125倍.(参考数据:)
A. 10 B. 11 C. 12 D. 13
【答案】C
【解析】
【分析】根据题意,化简,得,可得,利用参考数据,可得答案.
【详解】因为,所以.由题意,知,得,故被测标本的DNA大约扩增12次后,数量会变为原来的125倍.
故选:C
10. 设,,(其中e是自然对数的底数),则( )
A. B. C. D.
【答案】D
【解析】
【分析】构造,利用导数证明的的单调性,赋值可大致估计大小,,通过放缩可比较大小,进而得出答案.
【详解】设,得.令,解得.当时,,单调递减;
当时,,单调递增,所以,即,
则,,所以最小.
又因为,且,所以,所以.
综上所述,.
故选:D.
11. 已知正三棱柱的所有顶点都在球O的表面上,若球O的表面积为48π,则正三棱柱的体积的最大值为( )
A. B. C. D.
【答案】C
【解析】
【分析】结合正三棱柱和外接球关系先求出外接球半径,令正三棱柱底面边长为,由函数关系表示出体积与函数关系,利用导数可求最值.
【详解】如图,设正三棱柱上、下底面的中心分别为H,,连接.根据对称性可知,线段的中点O即为正三棱柱外接球的球心,线段OA即为该外接球的半径.由已知得,所以.设正三棱柱的底面边长为x,则.在中,,所以,所以正三棱柱的体积.
令,则,,故,.当时,,单调递增;当时,,单调递减,所以.
故选:C.
12. 已知的三个顶点都在抛物线上,点为的重心,直线经过该抛物线的焦点,则线段的长为( )
A. 8 B. 6 C. 5 D. 4.
【答案】B
【解析】
【分析】判断直线的斜率存在,设出直线方程,联立抛物线方程可得根与系数的关系式,利用三角形的重心即可求得参数k的值,根据抛物线的弦长公式即可求得答案.
【详解】设抛物线焦点为F,则.
根据题意可知,点为的重心,若直线的斜率不存在,
则不妨取,则结合重心可得C为,不合题意;
故直线的斜率存在,设直线的方程为,,
,,,则有,,,
联立方程得,,
则,,因为点为的重心,所以,
即,所以,
即,解得,
则,故线段AB的长为6,
故选:B.
【点睛】方法点睛:求解此类直线和圆锥曲线相交时的弦长问题,一般方法是设直线方程,联立圆锥曲线方程,利用根与系数的关系去化简求值;解答本题时要注意利用三角形重心的坐标公式并结合抛物线的性质,以及利用抛物线定义表示出弦长可使得计算简便.
二、填空题:本大题共4小题,每小题5分,共20分.
13. 已知向量满足,则_______.
【答案】
【解析】
【分析】通过平方方法化简已知条件,从而求得.
【详解】由两边平方得.
故答案为:
14. 在二项式的展开式中,各项的系数之和为512,则展开式中常数项的值为___________.
【答案】135
【解析】
【分析】根据各项的系数之和为512得到,解得,然后利用通项公式求常数项即可.
【详解】因为二项式的展开式中,各项的系数之和为512,所以令,得,解得.又因为的展开式的通项公式为,令,解得,所以展开式中常数项为.
故答案为:135.
15. 已知双曲线C:的左、右焦点分别为,,点P是双曲线C的右支上一点,若,且的面积为3,则双曲线C的焦距为___________.
【答案】
【解析】
【分析】根据双曲线定义结合余弦定理可推得,结合三角形面积可推得,由可得,继而推得,,再利用勾股定理结合即可求得c,可得答案.
【详解】设双曲线C:的半虚轴为b,半焦距为c,
由题意得,所以,
又,
两式相减可得,
则,所以,
又的面积为3,,所以,
得,所以,
因为,所以,即,
又因为,所以,,
所以,得,
又因为,且,所以,所以双曲线C的焦距为,
故答案为:.
16. 已知函数,若关于x的方程有8个不同的实数解,则整数m的值为___________.(其中e是自然对数的底数)
【答案】5
【解析】
【分析】判断函数的奇偶性,利用导数判断其单调性,继而作出其图象,数形结合,将关于x的方程有8个不同的实数解,转化为关于t的方程有2个不同的实数解,列出不等式组,即可求得答案.
【详解】因为,所以当时,,
当时,,即满足,则是偶函数.
当时,则,,当时,,单调递增;
当时,,单调递减;当时,,
作出函数的图象,如图所示:
设,因为有8个不同的实数解,
所以由图象可得,关于t的方程有2个不同的实数解,且都大于e,
所以有,解得,
又因为,所以整数m的值为5,
故答案为:5.
【点睛】方法点睛:解决此类比较复杂方程的根的个数问题,一般方法是采用换元法,数形结合,将根的个数问题转化为函数图象的交点问题;本题即根据函数解析式判断奇偶性,利用导数判断单调性,从而作出其图象,数形结合,将方程根的问题转化为图象交点问题,换元继而转化为关于t的方程有2个不同的实数解的问题.
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答;第22、23题为选考题,考生根据要求作答,
17. 已知a,b,c为的内角A,B,C所对的边,向量,且.
(1)求角C
(2)若,D为的中点,,求的面积.
【答案】(1)
(2)
【解析】
【分析】(1)根据向量垂直可得数量积为0,结合正余弦定理边角互化即可求解,
(2)根据余弦定理可求值,进而可求,根据三角形面积公式即可求解.
【小问1详解】
因为,所以,
由正弦定理得.
即,由余弦定理得,
因为,所以.
【小问2详解】
在三角形中,,
即,解得或,即或,
因为,故,
因为,所以,故,所以,
所以.
18. 全国中学生生物学竞赛隆重举行.为做好考试的评价工作,将本次成绩转化为百分制,现从中随机抽取了50名学生的成绩,经统计,这批学生的成绩全部介于40至100之间,将数据按照[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]分成6组,制成了如图所示的频率分布直方图.
(1)求频率分布直方图中的值,并估计这50名学生成绩的中位数;
(2)在这50名学生中用分层抽样的方法从成绩在[70,80),[80,90),[90,100]的三组中抽取了11人,再从这11人中随机抽取3人,记为3人中成绩在[80,90)的人数,求的分布列和数学期望;
【答案】(1),中位数;
(2)分布列见解析,.
【解析】
【分析】(1)根据频率分布直方图中所有小矩形的面积为1,结合中位数的定义进行求解即可;
(2)根据分层抽样的性质,结合古典概型公式、数学期望公式进行求解即可.
【小问1详解】
由频率分布直方图的性质可得,,
解得,
设中位数为, 解得;
【小问2详解】
的三组频率之比为0.28:0.12:0.04=7:3:1
从中分别抽取7人,3人,1人,
所有可能取值为0,1,2,3,
,,,
故的分布列为:
0 | 1 | 2 | 3 | |
故
19. 如图,四棱柱中,底面是矩形,且,,,若为的中点,且.
(1)求证:平面;
(2)线段上是否存在一点,使得二面角的大小为?若存在,求出的长;若不存在,说明理由.
【答案】(1)证明见解析;(2)存在,理由见解析.
【解析】
【分析】(1)由已知得为等边三角形,,再由,能证明⊥平面.
(2)过作,以为原点,建立空间直角坐标系,利用向量法能求出当的长为时,二面角的值为
【详解】(1)证明:∵,且,
∴为等边三角形
∵为的中点
∴,
又,且,
∴平面.
(2)过作,以为原点,建立空间直角坐标系(如图)
则,,
设,
平面的法向量为,
∵,,
且,
取,得
平面的一个法向量为
由题意得,
解得或(舍去),此时
∴当的长为时,二面角的值为.
20. 已知曲线C上的任意一点到点的距离和它到直线l:的距离的比是常数,过点F作不与x轴重合的直线与曲线C相交于A,B两点,过点A作AP垂直于直线l,交直线l于点P,直线PB与x轴相交于点M.
(1)求曲线C的方程;
(2)求面积的最大值.
【答案】(1)
(2)
【解析】
【分析】(1)由题意列出曲线方程化简即可求解;
(2)设直线AB的方程为,,,表示出,联立直线与椭圆方程消去,表示出关于的韦达定理,结合求出直接PB的方程,令,求出坐标,进而得到,由求出面积,结合换元法和对勾函数性质可求面积的最大值.
【小问1详解】
设曲线C上的任意一点的坐标为,
由题意,得,即,所以曲线C的方程为;
【小问2详解】
由题意,设直线AB的方程为,,,则.
联立方程得,则,
所以,,所以.
又因为,所以直线PB的方程为.
令,则,
所以,.
因为
,
所以.
令,,则.
又因为在上单调递减,所以当时,,
故面积的最大值为.
【点睛】方法点睛:利用韦达定理法解决直线与圆锥曲线相交问题的基本步骤如下:
(1)设直线方程,设交点坐标为;
(2)联立直线与圆锥曲线的方程,得到关于(或)的一元二次方程,必要时计算;
(3)列出韦达定理;
(4)将所求问题或题中的关系转化为、(或、)的形式;
(5)代入韦达定理求解.
21. 已知函数在处的切线方程为.
(1)求实数m和n的值;
(2)已知,是函数的图象上两点,且,求证:.
【答案】(1)
(2)证明见解析
【解析】
【分析】(1)先求导,由可求对应的m和n的值;
(2)设,由可判断,由得,设,,,得,代换整理得,原不等式要证,只需证,全部代换为关于的不等式得,设,,由导数得,再证,放缩得,进而得证.
【小问1详解】
由,得.
因为函数在处的切线方程为,
所以,,则;
【小问2详解】
证明:由(1)可得,,,
所以当时,,单调递增;
当时,,单调递减.
因为,是函数的图象上两点,且,
不妨设,且,所以.
由,得,即.
设,.
设,则,所以,
即,故.
要证,只需证,
即证,即证,即证,
即证,即证.
令,,
则,
证明不等式;
设,则,
所以当时,;当时,,
所以在上为增函数,在上为减函数,
故,所以成立.
由上还不等式可得,当时,,故恒成立,
故在上为减函数,则,
所以成立,即成立.
综上所述,.
22. 在平面直角坐标系xOy中,已知直线l的参数方程为(t为参数),以坐标原点O为极点,x轴的非负半轴为极轴(取相同的长度单位),建立极坐标系,曲线C的极坐标方程为.
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)若点P的极坐标为,直线l与曲线C相交于A,B两点,求的值.
【答案】(1);
(2)
【解析】
【分析】(1)利用消元法将参数方程化为普通方程即可得到直线l的普通方程;利用极坐标方程与直角坐标方程的转化公式即可得到曲线C的直角坐标方程;
(2)将点P的极坐标化为直角坐标判断得P在直线l上,再利用直线参数方程中参数的几何意义,将直线l代入曲线C的直角坐标方程,结合韦达定理即可求解.
【小问1详解】
因为直线l的参数方程为(t为参数),
所以直线l的普通方程为;
因为,即,
所以,得,
所以曲线C的直角坐标方程为.
【小问2详解】
因为点P的极坐标为,所以点P的直角坐标为,所以点P在直线l上,
将直线l的参数方程(t为参数),代入,化简得,
设A,B两点所对应的参数分别为,,则,,故,,
所以,,
所以.
23. 已知函数,M为不等式的解集.
(1)求集合M;
(2)设a,,求证:.
【答案】(1)
(2)证明见解析
【解析】
【分析】(1)采用零点讨论法去绝对值可直接求解;
(2)结合绝对值三角不等式得,要证,即证,即证,去平方结合因式分解即可求证.
【小问1详解】
①当时,不等式可化为,解得,则;
②当,不等式可化为,解得,则;
③当时,不等式可化为,解得,则.
综上所述,;
【小问2详解】
证明:因为(当且仅当时取等号),
所以要证,只需证,
即证,即证,即证,
即证.
由(1)可知,.
因为a,,所以,所以成立.
综上所述,.
四川省成都市石室中学2023-2024学年高三上学期期中理科数学试卷(Word版附解析): 这是一份四川省成都市石室中学2023-2024学年高三上学期期中理科数学试卷(Word版附解析),共23页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
【期中真题】四川省成都市第七中学2022-2023学年高二上学期期中数学理科试题.zip: 这是一份【期中真题】四川省成都市第七中学2022-2023学年高二上学期期中数学理科试题.zip,文件包含期中真题四川省成都市第七中学2022-2023学年高二上学期期中数学理科试题原卷版docx、期中真题四川省成都市第七中学2022-2023学年高二上学期期中数学理科试题解析版docx等2份试卷配套教学资源,其中试卷共24页, 欢迎下载使用。
【期中真题】四川省成都市第七中学2022-2023学年高三上学期期中考试理科数学试题.zip: 这是一份【期中真题】四川省成都市第七中学2022-2023学年高三上学期期中考试理科数学试题.zip,文件包含期中真题四川省成都市第七中学2022-2023学年高三上学期期中考试理科数学试题原卷版docx、期中真题四川省成都市第七中学2022-2023学年高三上学期期中考试理科数学试题解析版docx等2份试卷配套教学资源,其中试卷共27页, 欢迎下载使用。












