
2024年数学高考大一轮复习第十章 §10.5 列联表与独立性检验(附答单独案解析)
展开§10.5 列联表与独立性检验
考试要求 1.通过实例,理解2×2列联表的统计意义.2.通过实例,了解独立性检验及其应用.
知识梳理
1.分类变量:变量的不同“值”表示个体所属的不同类别,像这样的变量称为分类变量.
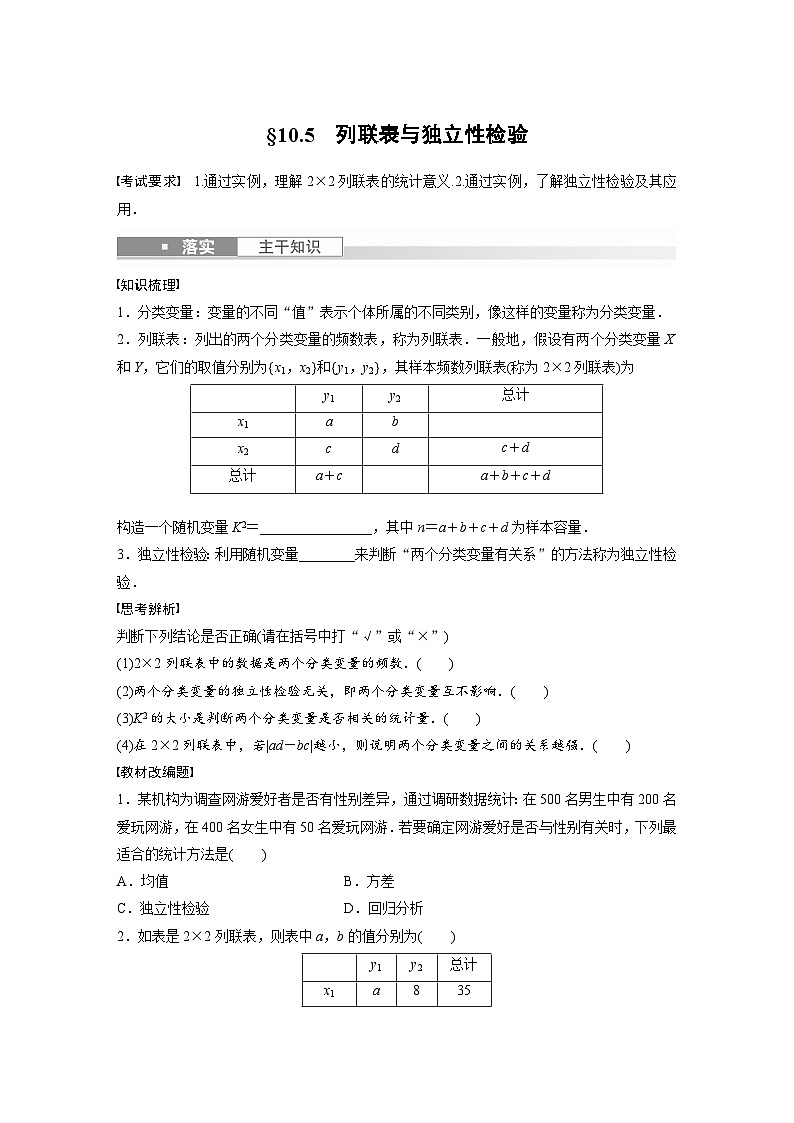
2.列联表:列出的两个分类变量的频数表,称为列联表.一般地,假设有两个分类变量X和Y,它们的取值分别为{x1,x2}和{y1,y2},其样本频数列联表(称为2×2列联表)为
| y1 | y2 | 总计 |
x1 | a | b |
|
x2 | c | d | c+d |
总计 | a+c |
| a+b+c+d |
构造一个随机变量K2=________________,其中n=a+b+c+d为样本容量.
3.独立性检验:利用随机变量________来判断“两个分类变量有关系”的方法称为独立性检验.
思考辨析
判断下列结论是否正确(请在括号中打“√”或“×”)
(1)2×2列联表中的数据是两个分类变量的频数.( )
(2)两个分类变量的独立性检验无关,即两个分类变量互不影响.( )
(3)K2的大小是判断两个分类变量是否相关的统计量.( )
(4)在2×2列联表中,若|ad-bc|越小,则说明两个分类变量之间的关系越强.( )
教材改编题
1.某机构为调查网游爱好者是否有性别差异,通过调研数据统计:在500名男生中有200名爱玩网游,在400名女生中有50名爱玩网游.若要确定网游爱好是否与性别有关时,下列最适合的统计方法是( )
A.均值 B.方差
C.独立性检验 D.回归分析
2.如表是2×2列联表,则表中a,b的值分别为( )
| y1 | y2 | 总计 |
x1 | a | 8 | 35 |
x2 | 11 | 34 | 45 |
总计 | b | 42 | 80 |
A.27,38 B.28,38
C.27,37 D.28,37
3.已知P(K2≥6.635)=0.01,P(K2≥10.828)=0.001.在检验喜欢某项体育运动是否与性别有关的过程中,某研究员搜集数据并计算得到K2=7.235,则有________的把握认为喜欢该项体育运动与性别有关.
题型一 列联表与K2的计算
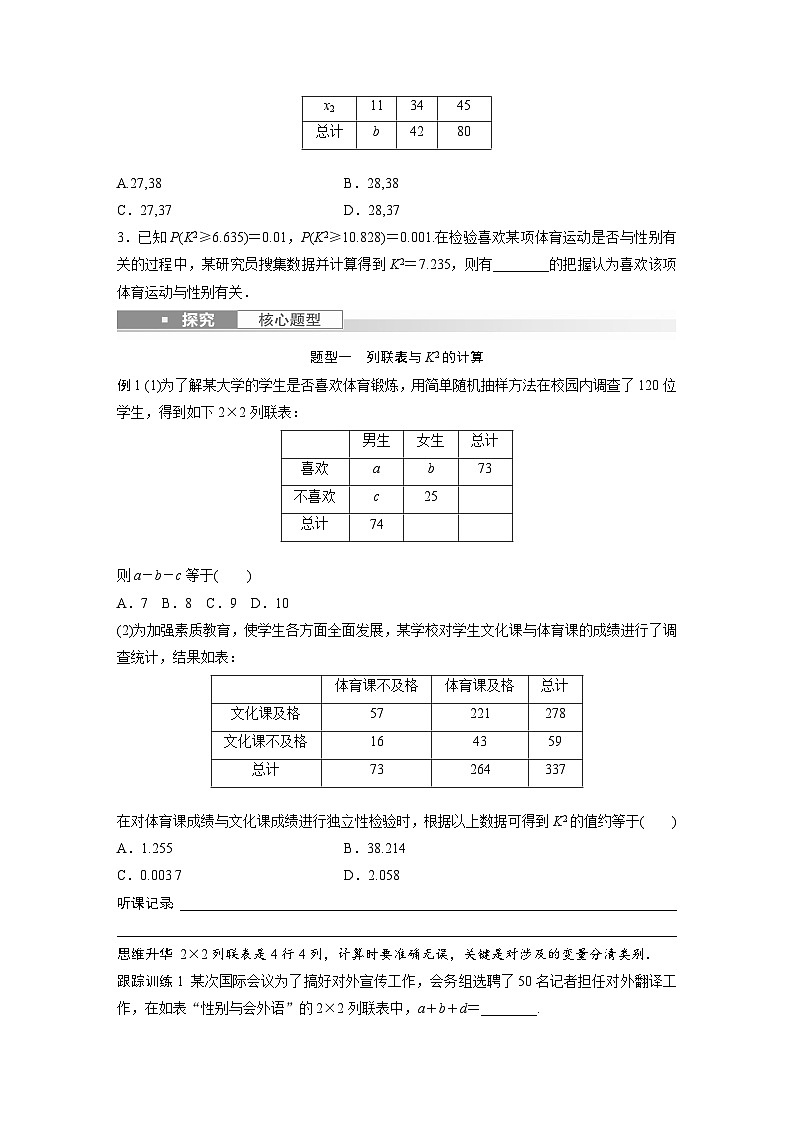
例1 (1)为了解某大学的学生是否喜欢体育锻炼,用简单随机抽样方法在校园内调查了120位学生,得到如下2×2列联表:
| 男生 | 女生 | 总计 |
喜欢 | a | b | 73 |
不喜欢 | c | 25 |
|
总计 | 74 |
|
|
则a-b-c等于( )
A.7 B.8 C.9 D.10
(2)为加强素质教育,使学生各方面全面发展,某学校对学生文化课与体育课的成绩进行了调查统计,结果如表:
| 体育课不及格 | 体育课及格 | 总计 |
文化课及格 | 57 | 221 | 278 |
文化课不及格 | 16 | 43 | 59 |
总计 | 73 | 264 | 337 |
在对体育课成绩与文化课成绩进行独立性检验时,根据以上数据可得到K2的值约等于( )
A.1.255 B.38.214
C.0.003 7 D.2.058
听课记录:_______________________________________________________________________
________________________________________________________________________________
思维升华 2×2列联表是4行4列,计算时要准确无误,关键是对涉及的变量分清类别.
跟踪训练1 某次国际会议为了搞好对外宣传工作,会务组选聘了50名记者担任对外翻译工作,在如表“性别与会外语”的2×2列联表中,a+b+d=________.
| 会外语 | 不会外语 | 总计 |
男 | a | b | 20 |
女 | 6 | d |
|
总计 | 18 |
| 50 |
题型二 列联表与独立性检验
例2 (12分)(2022·全国甲卷)甲、乙两城之间的长途客车均由A和B两家公司运营.为了解这两家公司长途客车的运行情况,随机调查了甲、乙两城之间的500个班次,得到下面列联表:
| 准点班次数 | 未准点班次数 |
A | 240 | 20 |
B | 210 | 30 |
(1)根据上表,分别估计这两家公司在甲、乙两城之间长途客车准点的概率;[切入点:古典概型]
(2)能否有90%的把握认为甲、乙两城之间的长途客车是否准点与客车所属公司有关?[关键点:K2的计算比较]
P(K2≥k0) | 0.1 | 0.05 | 0.01 |
k0 | 2.706 | 3.841 | 6.635 |
思维升华 独立性检验的一般步骤
(1)根据样本数据制成2×2列联表.
(2)计算K2=,其中n=a+b+c+d.
(3)比较K2与临界值的大小关系,作统计推断.
跟踪训练2 为了减少自身消费的碳排放,“绿色消费”等绿色生活方式渐成风尚.为获得不同年龄段的人对“绿色消费”意义的认知情况,某地研究机构将“90后与00后”作为A组,将“70后与80后”作为B组,并从A,B两组中各随机选取了100人进行问卷调查,整理数据后获得如下列联表:
单位:人
| 知晓 | 不知晓 | 总计 |
A组 | 75 | 25 | 100 |
B组 | 45 | 55 | 100 |
总计 | 120 | 80 | 200 |
附:K2=,n=a+b+c+d.
P(K2≥k0) | 0.1 | 0.05 | 0.01 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
(1)若从样本内知晓“绿色消费”意义的120人中用分层抽样的方法随机抽取16人,应在A组、B组中各抽取多少人?
(2)能否有99.9%的把握认为对“绿色消费”意义的认知情况与年龄有关?
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
题型三 独立性检验的综合应用
例3 体育运动是强身健体的重要途径,《中国儿童青少年体育健康促进行动方案(2020-2030)》(下面简称“体育健康促进行动方案”)中明确提出青少年学生每天在校内参与不少于60分钟的中高强度身体活动的要求.随着“体育健康促进行动方案”的发布,体育运动受到各地中小学的高度重视,众多青少年的体质健康得到很大的改善.某中学教师为了了解体育运动对学生的数学成绩的影响情况,现从该中学高三年级的一次月考中随机抽取1 000名学生,调查他们平均每天的体育运动情况以及本次月考的数学成绩(单位:分)情况,得到如表数据:
数学 成绩 | [30,50) | [50,70) | [70,90) | [90,110) | [110,130) | [130,150] |
人数 | 25 | 125 | 350 | 300 | 150 | 50 |
运动达标人数 | 10 | 45 | 145 | 200 | 107 | 43 |
约定:平均每天进行体育运动的时间不少于60分钟的为“运动达标”,数学成绩排在年级前50%以内(含50%)的为“数学成绩达标”.
(1)请估计该中学高三年级本次月考数学成绩的平均分(同一组中的数据用该组区间的中点值作代表);
(2)完成2×2列联表,并判断能否有99.9%的把握认为“数学成绩达标”与“运动达标”有关.
单位:人
| 数学成绩达标 | 数学成绩不达标 | 总计 |
运动达标 |
|
|
|
运动 |
|
|
|
不达标 |
|
|
|
总计 |
|
|
|
附:K2=,n=a+b+c+d.
P(K2≥k0) | 0.010 | 0.005 | 0.001 |
k0 | 6.635 | 7.879 | 10.828 |
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
思维升华 独立性检验的考查,往往与概率和抽样统计图等一起考查,这类问题的求解往往按各小题及提问的顺序,一步步进行下去,是比较容易解答的,考查单纯的独立性检验往往用小题的形式,而且K2的公式一般会在原题中给出.
跟踪训练3 某奶茶品牌公司计划在W市某区开设加盟分店,为了确定在该区开设分店的个数,该公司对该市已开设分店的5个区域的数据作了初步处理后得到下列表格,记x表示在5个区域开设分店的个数,y表示这x个分店的年收入之和.
x(个) | 2 | 3 | 4 | 5 | 6 |
y(十万元) | 2.5 | 3 | 4 | 4.5 | 6 |
参考公式:=,=-;
K2=,n=a+b+c+d.
临界值表:
P(K2≥k0) | 0.1 | 0.05 | 0.01 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
(1)该公司经过初步判断,可用线性回归模型拟合y与x的关系,求y关于x的线性回归方程;
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
(2)如果该公司最终决定在该区选择两个合适的地段各开设一个分店,根据市场调查得到如下统计数据,分店一每天的顾客平均为30人,其中5人会购买该品牌奶茶,分店二每天的顾客平均为80人,其中20人会购买该品牌奶茶.根据列联表判断是否有90%的把握认为顾客下单与分店所在地段有关.
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
2024年数学高考大一轮复习第十章 §10.5 列联表与独立性检验(附答单独案解析): 这是一份2024年数学高考大一轮复习第十章 §10.5 列联表与独立性检验(附答单独案解析),共7页。
2024年数学高考大一轮复习第十章 §10.4 回归分析(附答单独案解析): 这是一份2024年数学高考大一轮复习第十章 §10.4 回归分析(附答单独案解析),共5页。试卷主要包含了下列说法中不正确的是,对于相关系数,下列说法错误的是等内容,欢迎下载使用。
2024年数学高考大一轮复习第十章 §10.3 用样本估计总体(附答单独案解析): 这是一份2024年数学高考大一轮复习第十章 §10.3 用样本估计总体(附答单独案解析),共5页。













