

广东省深圳市光明区勤诚达学校2023-2024学年上学期九年级10月月考数学试卷
展开光明区勤诚达学校2023-2024学年第一学期九年级10月月考数学试卷
一.选择题(每题3分,共30分)
1.已知线段a、b、c、d是成比例线段,如果a=1,b=2,c=3,那么d的值是( )
A.8 B.6 C.4 D.1
2.在下列命题中,正确的是( )
A.一组对边平行的四边形是平行四边形
B.有一组邻边相等的平行四边形是菱形
C.有一个角是直角的四边形是矩形
D.对角线互相垂直平分的四边形是正方形
3.如图,某小区有一块长为18米、宽为6米的矩形空地,计划在其中修建两块相同的矩形绿地(图中阴影部分),它们的面积之和为60平方米,两块绿地之间及周边留有宽度相等的人行通道.若设人行通道的宽度为x米,则下列所列方程正确的是( )
A.(18﹣2x)(6﹣2x)=60 B.(18﹣3x)(6﹣x)=60
C.(18﹣2x)(6﹣x)=60 D.(18﹣3x)(6﹣2x)=60
4.下列两个三角形不一定相似的是( )
A.两个等边三角形
B.两个顶角是120°的等腰三角形
C.两个全等三角形
D.两个直角三角形
5.一个仅装有球的不透明盒子里,共有20个红球和白球(仅有颜色不同),小明进行了摸球试验,摸到红球可能性最大的是( )
A. B.
C. D.
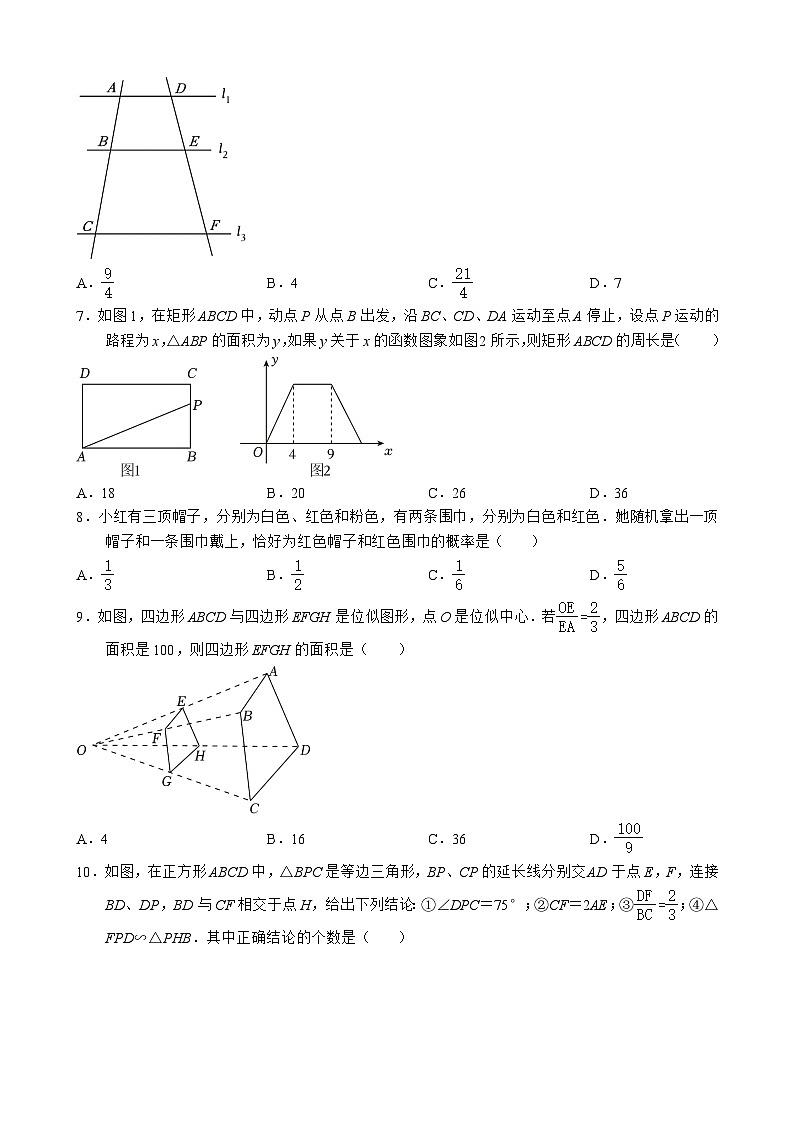
6.如图,直线l1∥l2∥l3,直线AC交l1、l2、l3于点A、B、C,直线DF交l1、l2、l3于点D、E、F,已知,若DE=3,则DF的长是( )
A. B.4 C. D.7
7.如图1,在矩形ABCD中,动点P从点B出发,沿BC、CD、DA运动至点A停止,设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则矩形ABCD的周长是( )
A.18 B.20 C.26 D.36
8.小红有三顶帽子,分别为白色、红色和粉色,有两条围巾,分别为白色和红色.她随机拿出一顶帽子和一条围巾戴上,恰好为红色帽子和红色围巾的概率是( )
A. B. C. D.
9.如图,四边形ABCD与四边形EFGH是位似图形,点O是位似中心.若,四边形ABCD的面积是100,则四边形EFGH的面积是( )
A.4 B.16 C.36 D.
10.如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E,F,连接BD、DP,BD与CF相交于点H,给出下列结论:①∠DPC=75°;②CF=2AE;③;④△FPD∽△PHB.其中正确结论的个数是( )
A.4 B.3 C.2 D.1
二.填空题(每题3分,共15分)
11.已知m2+n2+2m=﹣10+6n,则mn的值为 .
12.如图是小明的健康绿码示意图,用黑白打印机打印于边长为2cm的正方形区域内,为了估计图中黑色部分的总面积,在正方形区域内随机掷点,经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,据此可以估计黑色部分的总面积约为 cm2.
13.如图,数学活动课上,为测量学校旗杆高度,小艺同学在脚下水平放置一平面镜,然后向后退(保持脚、镜和旗杆底端在同一直线上),直到她刚好在镜子中看到旗杆的顶端.已知小艺的眼睛离地面高度为1.6米,同时量得小艺与镜子的水平距离为2米,镜子与旗杆的水平距离为10米,则旗杆的高度为 米.
14.如图,矩形ABCD中,AB=4,.以A为圆心,AD为半径作弧交BC于点E,则图中阴影部分的面积为 .
15.如图,折叠边长为4cm的正方形纸片ABCD,折痕是DM,点C落在点E处,分别延长ME、DE交AB于点F、G,若点M是BC边的中点,则FG= cm.
三.解答题(共55分)
16.(8分)解方程:
(1)4x2﹣3x﹣1=0; (2)x(x﹣4)=2﹣8x.
17.(9分)据中国载人航天工程办公室消息,“天宫课堂”第二课于2022年3月23日15时40分在中国空间站开讲,神舟十三号乘组航天员翟志刚、王亚平、叶光富将相互配合进行授课,这也是中国航天员第三次进行太空授课,届时,航天员将在轨演示太空“冰雪”实验、液桥演示实验,水油分离实验、太空抛物实验.
某中学为了解学生对“航空航天知识”的掌握情况,从初一年级800人随机抽取50名学生进行测试,并对成绩(百分制)进行整理,信息如下:
(Ⅰ)成绩频数分布表:
成绩x(分)
50≤x<60
60≤x<70
70≤x<80
80≤x<90
90≤x<100
频数
4
a
14
b
4
(Ⅱ)成绩在70≤x<80这一组的是(单位:分):
70 70 71 72 72 74 77 77 78 78 78 79 79 79
根据以上信息,回答下列问题:
(1)表中a= ,b= .在这次试中,成绩的中位数是 分,成绩不低于80分的人数占测试人数的百分比为 .
(2)这次测试成绩的平均数是76.6分,甲的测试成绩是77分.乙说:“甲的成绩高于平均数,所以甲的成绩高于一半学生的成绩.”你认为乙的说法正确吗?请说明理由.
(3)在90≤x<100之间的四名同学有两位男生和两位女生,学校打算选派一位男生和一位女生参加市里举办的“航空航天知识”,请求出选中一男一女的概率.
18.(7分)2023年杭州亚运会吉祥物一开售,就深受大家的喜爱.某商店以每件35元的价格购进某款亚运会吉祥物,以每件58元的价格出售.经统计,4月份的销售量为256件,6月份的销售量为400件.
(1)求该款吉祥物4月份到6月份销售量的月平均增长率;
(2)从7月份起,商场决定采用降价促销的方式回馈顾客,经试验,发现该吉祥物每降价1元,月销售量就会增加20件.当该吉祥物售价为多少元时,月销售利润达8400元?
19.(8分)如图,在矩形ABCD中,DE平分∠ADC,∠EDO=15°.
(1)试比较线段AO与AE的大小.并证明你的结论;
(2)连接OE,求∠AOE的大小.
20.(6分)园林部门计划在某公园建一个长方形花圃ABCD,花圃的一面靠墙(墙足够长),另外三边用木栏围成,如图2所示BC=2AB,建成后所用木栏总长120米,在图2总面积不变的情况下,园林部门在花圃内部设计了一个正方形的网红打卡点和两条宽度相等的小路如图3,小路的宽度是正方形网红打卡点边长的,其余部分种植花卉,
花卉种植的面积为1728平方米.
(1)求长方形ABCD花圃的长和宽;
(2)求出网红打卡点的面积.
21.(8分)如图,在矩形ABCD中,AB=8cm,BC=16cm,点P从点D出发向点A运动,运动到点A停止,同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s.连接PQ、AQ、CP.设点P、Q运动的时间为ts.
(1)当t为何值时,四边形ABQP是矩形;
(2)当t为何值时,四边形AQCP是菱形;
(3)分别求出(2)中菱形AQCP的周长和面积.
22.(9分)在矩形ABCD上有一个动点P,点P沿AD—DC—CA 运动,并且不与点A重合,连接BP,以BP为直角边作等腰直角三角形BPQ,AB=6,AD=4.
(1)当点P沿AD—DC—CA运动时,求出等腰直角三角形BPQ面积的最大值;
(2)当点P在AD上运动时,△BPQ的边PQ与DC交于点E,如图(1)所示,若AP:AD=1:2,则AB:PD等于 ;若 AP:AD=1:n,则AB:PD等于 ;
(3)如图(2)所示,当点P(不与点D,C重合)在DC上运动时,请你判断梯形ABPD的面积是否可以为△BPQ面积的4倍,若可以,请求出PC的长度;若不可以,请说明理由.
光明区勤诚达学校10月月考数学试卷参考答案与试题解析
一.选择题(共10小题)
1.已知线段a、b、c、d是成比例线段,如果a=1,b=2,c=3,那么d的值是( )
A.8 B.6 C.4 D.1
【解答】解:∵线段a、b、c、d是成比例线段,a=1,b=2,c=3,
∴a:b=c:d,
即1:2=3:d,
解得:d=6.
故选:B.
2.在下列命题中,正确的是( )
A.一组对边平行的四边形是平行四边形
B.有一组邻边相等的平行四边形是菱形
C.有一个角是直角的四边形是矩形
D.对角线互相垂直平分的四边形是正方形
【解答】解:A、一组对边平行且相等的四边形是平行四边形,故A选项错误;
B、有一组邻边相等的平行四边形是菱形,故B选项正确;
C、有一个角是直角的平行四边形是矩形,故C选项错误;
D、对角线互相垂直平分的四边形是菱形,故D选项错误.
故选:B.
3.如图,某小区有一块长为18米、宽为6米的矩形空地,计划在其中修建两块相同的矩形绿地(图中阴影部分),它们的面积之和为60平方米,两块绿地之间及周边留有宽度相等的人行通道.若设人行通道的宽度为x米,则下列所列方程正确的是( )
A.(18﹣2x)(6﹣2x)=60 B.(18﹣3x)(6﹣x)=60
C.(18﹣2x)(6﹣x)=60 D.(18﹣3x)(6﹣2x)=60
【解答】解:设人行通道的宽度为x米,根据题意可得:
(18﹣3x)(6﹣2x)=60,
故选:D.
4.下列两个三角形不一定相似的是( )
A.两个等边三角形
B.两个顶角是120°的等腰三角形
C.两个全等三角形
D.两个直角三角形
【解答】解:A、两个等边三角形,所有的角都是60°,相等,可以判定两三角形相似,故本选项错误;
B、两个顶角是120°的等腰三角形,两个底角一定都是30°,可以判定两三角形相似,故本选项错误;
C、全等是相似的特殊情况,两个全等三角形一定相似,故本选项错误;
D、两个直角三角形,只有一个直角对应相等,无法判定相似,故本选项正确.
故选:D.
5.一个仅装有球的不透明盒子里,共有20个红球和白球(仅有颜色不同),小明进行了摸球试验,摸到红球可能性最大的是( )
A. B.
C. D.
【解答】解:∵一个仅装有球的不透明盒子里,共有20个红球和白球(仅有颜色不同),0<4<10<16,
∴摸到红球可能性最大的是D选项.
故选:D.
6.如图,直线l1∥l2∥l3,直线AC交l1、l2、l3于点A、B、C,直线DF交l1、l2、l3于点D、E、F,已知,若DE=3,则DF的长是( )
A. B.4 C. D.7
【解答】解:∵直线l1∥l2∥l3,
∴=.
∵=,AC=AB+BC,
∴==,
∴EF=DE=4,
∴DF=DE+EF=7.
故选:D.
7.如图1,在矩形ABCD中,动点P从点B出发,沿BC、CD、DA运动至点A停止,设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则矩形ABCD的周长是( )
A.18 B.20 C.26 D.36
【解答】解:∵动点P从点B出发,沿BC、CD、DA运动至点A停止,而当点P运动到点C,D之间时,△ABP的面积不变,
函数图象上横轴表示点P运动的路程,x=4时,y开始不变,说明BC=4,x=9时,接着变化,说明CD=9﹣4=5,
∴AB=5,BC=4,
∴矩形ABCD的周长=2(AB+BC)=18.
故选:A.
8.小红有三顶帽子,分别为白色、红色和粉色,有两条围巾,分别为白色和红色.她随机拿出一顶帽子和一条围巾戴上,恰好为红色帽子和红色围巾的概率是( )
A. B. C. D.
【解答】解:画树状图为:
共有6种等可能的结果,其中恰好为红色帽子和红色围巾的结果数为1种,
所以恰好为红色帽子和红色围巾的概率=.
故选:C.
9.如图,四边形ABCD与四边形EFGH是位似图形,点O是位似中心.若,四边形ABCD的面积是100,则四边形EFGH的面积是( )
A.4 B.16 C.36 D.
【解答】解:∵四边形ABCD与四边形EFGH是位似图形,点O是位似中心,
∴四边形ABCD与四边形EFGH相似,=,
∵=,
∴=,
∴四边形EFGH的面积:四边形ABCD的面积=()2=()2=,
∴四边形EFGH的面积=×100=16.
故选:B.
10.如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E,F,连接BD、DP,BD与CF相交于点H,给出下列结论:①∠DPC=75°;②CF=2AE;③;④△FPD∽△PHB.其中正确结论的个数是( )
A.4 B.3 C.2 D.1
【解答】解:∵△BPC是等边三角形,
∴BP=PC=BC,∠PBC=∠PCB=∠BPC=60°,
∵四边形ABCD是正方形,
∴AB=BC=CD,∠A=∠ADC=∠BCD=90°,
∴∠ABE=∠DCF=30°,
∴∠CPD=∠CDP=75°,故①正确;
∵△BPC是等边三角形,
∴BP=PC=BC,∠PBC=∠PCB=∠BPC=60°,
∵四边形ABCD是正方形,
∴∠PEF=∠PFE=60°,
∴△PEF是等边三角形,
∴PE=PF,
∴CP+PF=CP+PE,
∴CF=BE,
在Rt△ABE中,
∠ABE=∠ABC﹣∠PBC=30°,
∴BE=2AE,
∴CF=2AE,故②正确;
∴∠PDE=15°,
∵∠PBD=∠PBC﹣∠HBC=60°﹣45°=15°,
∴∠EBD=∠EDP,
∵∠DEP=∠DEB,
∴△BDE∽△DPE,
∴∠EPD=∠BDE=45°,
∵∠BPC=∠EPF=60°,
∴∠FPD=105°,
∵∠BHP=∠BCH+∠HBC=105°,
∴∠DPF=∠BHP,
又∵∠PDF=∠DBP=15°,
∴△BHP∽△DPF,故④正确;
∴,
∴=,
∵∠DCF=30°,
∴DC=DF,
∴=,
∴==,故③错误,
故选:B.
二.填空题(共5小题)
11.已知m2+n2+2m=﹣10+6n,则mn的值为 ﹣1 .
【解答】解:∵m2+n2+2m=﹣10+6n,
∴m2+n2+2m+10﹣6n=0,
∴(m+1)2+(n﹣3)2=0,
∴m+1=0,n﹣3=0,
∴m=﹣1,n=3,
∴mn=(﹣1)3=﹣1.
故答案为:﹣1.
12.如图是小明的健康绿码示意图,用黑白打印机打印于边长为2cm的正方形区域内,为了估计图中黑色部分的总面积,在正方形区域内随机掷点,经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,据此可以估计黑色部分的总面积约为 2.4 cm2.
【解答】解:∵经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,
∴点落入黑色部分的概率为0.6,
∵边长为2cm的正方形的面积为4cm2,
设黑色部分的面积为S,
则=0.6,
解得S=2.4(cm2).
∴估计黑色部分的总面积约为2.4cm2.
故答案为:2.4.
13.如图,数学活动课上,为测量学校旗杆高度,小艺同学在脚下水平放置一平面镜,然后向后退(保持脚、镜和旗杆底端在同一直线上),直到她刚好在镜子中看到旗杆的顶端.已知小艺的眼睛离地面高度为1.6米,同时量得小艺与镜子的水平距离为2米,镜子与旗杆的水平距离为10米,则旗杆的高度为 8 米.
【解答】解:由题意得:∠ABO=∠CDO=90°,∠AOB=∠COD,
∴△AOB∽△COD,
∴=,
∵AB=1.6米,OB=2米,OD=10米,
∴=,
解得:CD=8,
∴旗杆的高度为8米,
故答案为:8.
14.如图,矩形ABCD中,AB=4,.以A为圆心,AD为半径作弧交BC于点E,则图中阴影部分的面积为 16﹣8﹣4π .
【解答】解:由题意得:AE=AD=4,
∵四边形ABCD是矩形,
∴∠B=∠BAD=90°,
∵AB=4,
∴BE==4,
∴△ABE是等腰直角三角形,
∴∠BAE=45°,
∴∠DAE=45°,
∵矩形ABCD的面积=AD•AB=16,扇形AED的面积==4π,△ABE的面积=AB•BE=8,
∴阴影的面积=矩形ABCD的面积﹣扇形AED的面积﹣△ABE的面积=16﹣8﹣4π.
故答案为:16﹣8﹣4π.
15.如图,折叠边长为4cm的正方形纸片ABCD,折痕是DM,点C落在点E处,分别延长ME、DE交AB于点F、G,若点M是BC边的中点,则FG= cm.
【解答】解:如图,连接DF,
∵四边形ABCD是正方形,
∴AD=CD=AB=BC=4cm,∠A=∠B=∠C=90°,
∵点M是BC边的中点,
∴CM=BM=BC=2cm,
由折叠得:DE=CD=4cm,EM=CM=2cm,∠DEM=∠C=90°,
∴∠DEF=180°﹣90°=90°,AD=DE,
∴∠A=∠DEF,
在Rt△DAF和Rt△DEF中,
,
∴Rt△DAF≌Rt△DEF(HL),
∴AF=EF,
设AF=xcm,则EF=xcm,
∴BF=(4﹣x)cm,FM=(x+2)cm,
在Rt△BFM中,BF2+BM2=FM2,
∴(4﹣x)2+22=(x+2)2,
解得:x=,
∴AF=EF=cm,BF=4﹣=cm,FM=+2=cm,
∵∠FEG=∠DEM=90°,
∴∠FEG=∠B=90°,
∵∠EFG=∠BFM,
∴△FGE∽△FMB,
∴=,即=,
∴FG=cm,
故答案为:.
三.解答题(共7小题)
16.解方程:
(1)4x2﹣3x﹣1=0; (2)x(x﹣4)=2﹣8x.
【解答】解:(1)x1=-,x2=1.
(2)x(x﹣4)=2﹣8x
整理得x2+4x﹣2=0,
∵a=1,b=4,c=﹣2,
∴Δ=b2﹣4ac=16+8=24,
∴x=.
即x1=﹣2+,x2=﹣2﹣.
17.据中国载人航天工程办公室消息,“天宫课堂”第二课于2022年3月23日15时40分在中国空间站开讲,神舟十三号乘组航天员翟志刚、王亚平、叶光富将相互配合进行授课,这也是中国航天员第三次进行太空授课,届时,航天员将在轨演示太空“冰雪”实验、液桥演示实验,水油分离实验、太空抛物实验.
某中学为了解学生对“航空航天知识”的掌握情况,从初一年级800人随机抽取50名学生进行测试,并对成绩(百分制)进行整理,信息如下:
(Ⅰ)成绩频数分布表:
成绩x(分)
50≤x<60
60≤x<70
70≤x<80
80≤x<90
90≤x<100
频数
4
a
14
b
4
(Ⅱ)成绩在70≤x<80这一组的是(单位:分):
70 70 71 72 72 74 77 77 78 78 78 79 79 79
根据以上信息,回答下列问题:
(1)表中a= 10 ,b= 18 .在这次试中,成绩的中位数是 78.5 分,成绩不低于80分的人数占测试人数的百分比为 44% .
(2)这次测试成绩的平均数是76.6分,甲的测试成绩是77分.乙说:“甲的成绩高于平均数,所以甲的成绩高于一半学生的成绩.”你认为乙的说法正确吗?请说明理由.
(3)在90≤x<100之间的四名同学有两位男生和两位女生,学校打算选派一位男生和一位女生参加市里举办的“航空航天知识”,请求出选中一男一女的概率.
【解答】解:(1)a=50×20%=10,b=50﹣4﹣10﹣14﹣4=18,
将这50名学生的成绩从小到大排列,处在中间位置的两个数的平均数为=78.5,因此中位数是78.5,
成绩不低于80分的人数占测试人数的百分比为,
故答案为:10,18,78.5,44%;
(2)不正确,利用中位数进行判断比较合理,由于中位数是78.5分,甲的测试成绩是77分,因此甲的成绩在一半以下;
(3)从2男2女中随机选取2人所有等可能出现的结果如下:
共有12种等可能出现的结果,其中1男1女的有8种,
所以从2男2女中随机选取2人是一男一女的概率为=.
18.2023年杭州亚运会吉祥物一开售,就深受大家的喜爱.某商店以每件35元的价格购进某款亚运会吉祥物,以每件58元的价格出售.经统计,4月份的销售量为256件,6月份的销售量为400件.
(1)求该款吉祥物4月份到6月份销售量的月平均增长率;
(2)从7月份起,商场决定采用降价促销的方式回馈顾客,经试验,发现该吉祥物每降价1元,月销售量就会增加20件.当该吉祥物售价为多少元时,月销售利润达8400元?
【解答】解:(1)设该款吉祥物4月份到6月份销售量的月平均增长率为x,
根据题意得:256(1+x)2=400,
解得:x1=0.25=25%,x2=﹣2.25(不符合题意,舍去).
答:该款吉祥物4月份到6月份销售量的月平均增长率为25%;
(2)设该吉祥物售价为y元,则每件的销售利润为(y﹣35)元,月销售量为400+20(58﹣y)=(1560﹣20y)件,
根据题意得:(y﹣35)(1560﹣20y)=8400,
整理得:y2﹣113y+3150=0,
解得:y1=50,y2=63(不符合题意,舍去).
答:该款吉祥物售价为50元时,月销售利润达8400元.
19.如图,在矩形ABCD中,DE平分∠ADC,∠EDO=15°.
(1)试比较线段AO与AE的大小.并证明你的结论;
(2)连接OE,求∠AOE的大小.
【解答】解:(1)AO=AE;理由如下:
∵四边形ABCD是矩形,
∴∠ADC=∠BAD=90°,AO=DO,
∵DE平分∠ADC
∴∠CDE=∠ADE=45°,
∴△ADE是等腰直角三角形,
∴AD=AE,
又∵∠EDO=15°,
∴∠ADO=60°;
∴△OAD是等边三角形;
∴AD=AO=DO,
∴AO=AE;
(2)∵△OAD是等边三角形,
∴∠DAO=60°,
∴∠OAE=90°﹣∠DAO=30°,
∵AO=AE,
∴∠AOE=(180°﹣30°)÷2=75°.
20.园林部门计划在某公园建一个长方形花圃ABCD,花圃的一面靠墙(墙足够长),另外三边用木栏围成,如图2所示BC=2AB,建成后所用木栏总长120米,在图2总面积不变的情况下,园林部门在花圃内部设计了一个正方形的网红打卡点和两条宽度相等的小路如图3,小路的宽度是正方形网红打卡点边长的,其余部分种植花卉,
花卉种植的面积为1728平方米.
(1)求长方形ABCD花圃的长和宽;
(2)求出网红打卡点的面积.
【解答】解:(1)设AB=x米,
∴BC=2AB=2x米,
根据题意,得2x+x+x=120,
解得x=30,
∴AB=30米,BC=60米,
答:长方形ABCD花圃的长为60米,宽为30米;
(2)设网红打卡点的边长为m米,
根据题意,得(60﹣m)+m2=60×30﹣1728,
解得m1=4,m2=﹣24(舍去),
∴网红打卡点的面积为4×4=16(平方米),
答:网红打卡点的面积为16平方米.
21.如图,在矩形ABCD中,AB=8cm,BC=16cm,点P从点D出发向点A运动,运动到点A停止,同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s.连接PQ、AQ、CP.设点P、Q运动的时间为ts.
(1)当t为何值时,四边形ABQP是矩形;
(2)当t为何值时,四边形AQCP是菱形;
(3)分别求出(2)中菱形AQCP的周长和面积.
【解答】解:(1)∵在矩形ABCD中,AB=8cm,BC=16cm,
∴BC=AD=16cm,AB=CD=8cm,
由已知可得,BQ=DP=tcm,AP=CQ=(16﹣t)cm,
在矩形ABCD中,∠B=90°,AD∥BC,
当BQ=AP时,四边形ABQP为矩形,
∴t=16﹣t,得t=8,
故当t=8s时,四边形ABQP为矩形;
(2)∵AP=CQ,AP∥CQ,
∴四边形AQCP为平行四边形,
∴当AQ=CQ时,四边形AQCP为菱形
即=16﹣t时,四边形AQCP为菱形,解得t=6,
故当t=6s时,四边形AQCP为菱形;
(3)当t=6s时,AQ=CQ=CP=AP=16﹣6=10cm,
则周长为4×10cm=40cm;
面积为10cm×8cm=80cm2.
22.在矩形ABCD上有一个动点P,点P沿AD—DC—CA 运动,并且不与点A重合,连接BP,以BP为直角边作等腰直角三角形BPQ,AB=6,AD=4.
(1)当点P沿AD—DC—CA运动时,求出等腰直角三角形BPQ面积的最大值;
(2)当点P在AD上运动时,△BPQ的边PQ与DC交于点E,如图(1)所示,若AP:AD=1:2,则AB:PD等于 3 ;若 AP:AD=1:n,则AB:PD等于 ;
(3)如图(2)所示,当点P(不与点D,C重合)在DC上运动时,请你判断梯形ABPD的面积是否可以为△BPQ面积的4倍,若可以,请求出PC的长度;若不可以,请说明理由.
【解答】解(1)∵当点P移动到点D处时,BP>BA>BC,此时BP=BD==(最大),
∵△BPQ是等腰直角三角形,
∴△BPQ的面积=BP2=×()2=26,
即P点运动到D点的时,△BPQ有面积的最大值26;
(2)如图1,当AP:AD=1:2时,AP=PD=AD=2,
此时,AB:PD=6:2=3,
当AP:AD=1:n时,AP=AD×=,
∴PD=AD﹣AP=4﹣=,
∴AB:PD=6:=,
故答案为:3,;
(3)不存在,理由如下:
如图2,设PC=y,
则DP=6﹣y,BP2=42+y2,
若梯形ABPD的面积=4×△BPQ的面积,
则[(6﹣y)+6]×4=4×(42+y2),
即y2+y+4=0,其中Δ=﹣15<0,
∴该方程无解,
∴当P点在DC上运动时,梯形ABPD的面积不可能是等腰直角三角形BPQ的面积的4倍.
精品解析:2023年广东省深圳市光明区勤诚达学校中考数学三模试题: 这是一份精品解析:2023年广东省深圳市光明区勤诚达学校中考数学三模试题,文件包含精品解析2023年广东省深圳市光明区勤诚达学校中考数学三模试题原卷版docx、精品解析2023年广东省深圳市光明区勤诚达学校中考数学三模试题解析版docx等2份试卷配套教学资源,其中试卷共32页, 欢迎下载使用。
2023-2024学年广东省深圳市光明区勤诚达学校九年级(上)月考数学试卷(10月份)(含解析): 这是一份2023-2024学年广东省深圳市光明区勤诚达学校九年级(上)月考数学试卷(10月份)(含解析),共20页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
广东省深圳市光明区勤诚达学校2023-2024学年上学期九年级10月月考数学试卷: 这是一份广东省深圳市光明区勤诚达学校2023-2024学年上学期九年级10月月考数学试卷,共6页。












