





浙江省浙南名校联盟2023-2024学年高三上学期第一次联考数学试题含解析
展开这是一份浙江省浙南名校联盟2023-2024学年高三上学期第一次联考数学试题含解析,文件包含浙江省浙南名校联盟2023-2024学年高三上学期第一次联考数学试题Word版含解析docx、浙江省浙南名校联盟2023-2024学年高三上学期第一次联考数学试题Word版含解析docx、浙江省浙南名校联盟2023-2024学年高三上学期第一次联考数学试题Word版无答案docx、浙江省浙南名校联盟2023-2024学年高三上学期第一次联考数学试题Word版无答案docx等4份试卷配套教学资源,其中试卷共62页, 欢迎下载使用。
绝密★考试结束前
2023学年第一学期浙南名校联盟第一次联考
高三年级数学学科试题
考生须知:
1.本卷共5页满分150分,考试时间120分钟.
2.答题前,在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号并填涂相应数字.
3.所有答案必须写在答题纸上,写在试卷上无效.
4.考试结束后,只需上交答题纸.
选择题部分
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知集合,则( )
A. B. C. D.
2. 双曲线的焦点坐标为( )
A B. C. D.
3. 已知平面向量,则在方向上的投影向量为( )
A. B. C. D.
4. 已知,则“”是“数列是递增数列”的( )
A. 充分不必要条件 B. 必要不充分条
C. 充要条件件 D. 既不充分又不必要条件
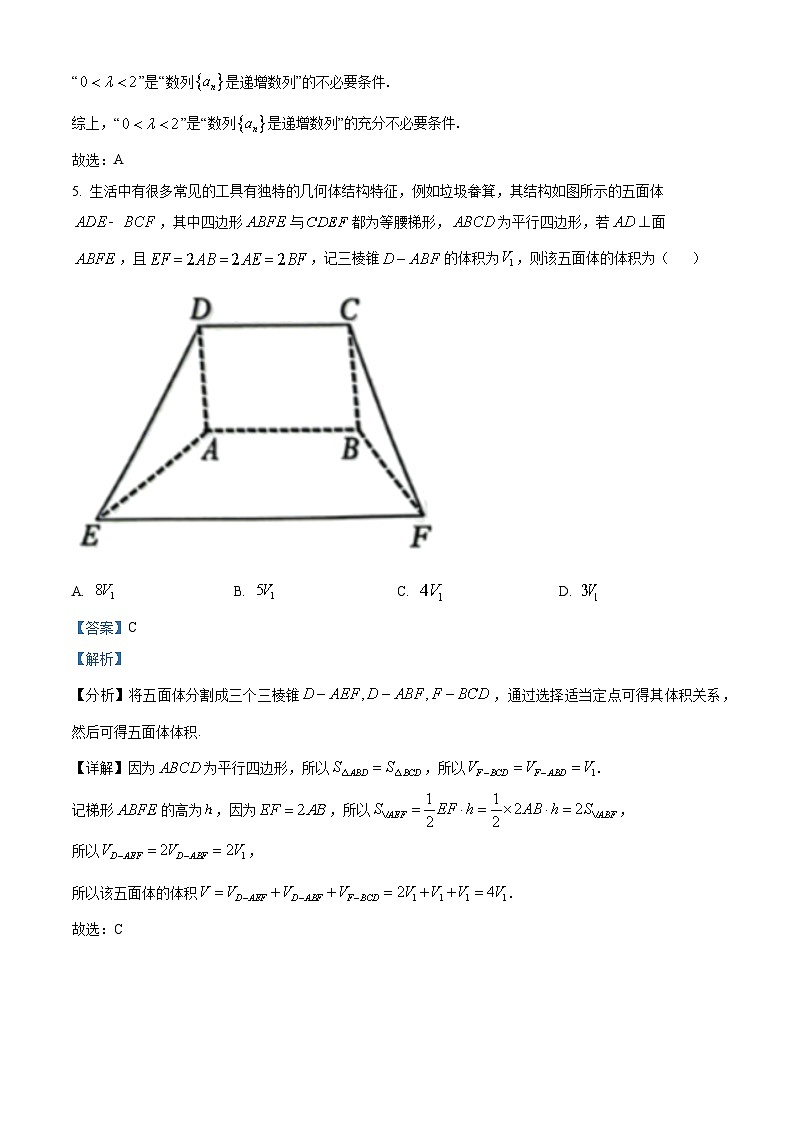
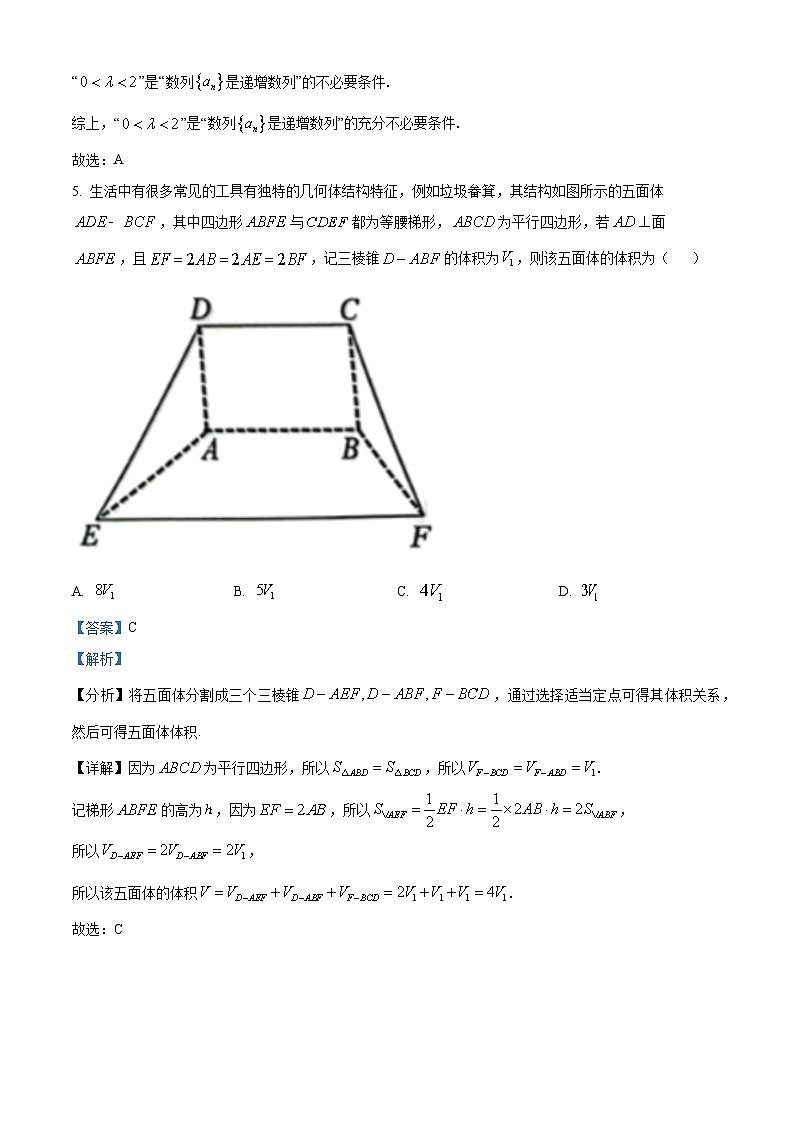
5. 生活中有很多常见的工具有独特的几何体结构特征,例如垃圾畚箕,其结构如图所示的五面体,其中四边形与都为等腰梯形,为平行四边形,若面,且,记三棱锥的体积为,则该五面体的体积为( )
A. B. C. D.
6. 若,则的值为( )
A. B. C. D.
7. 设离散型随机变量的期望和方差分别为和,且,则( )
A.
B
C.
D. 和大小不确定
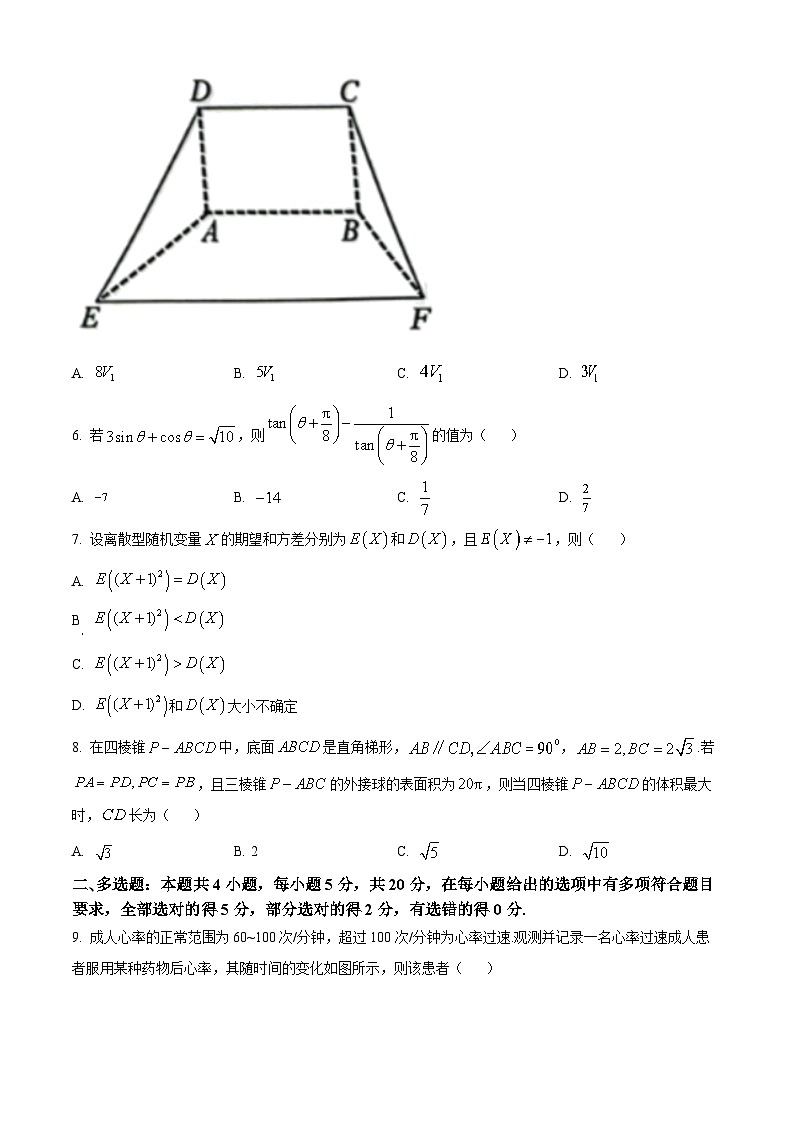
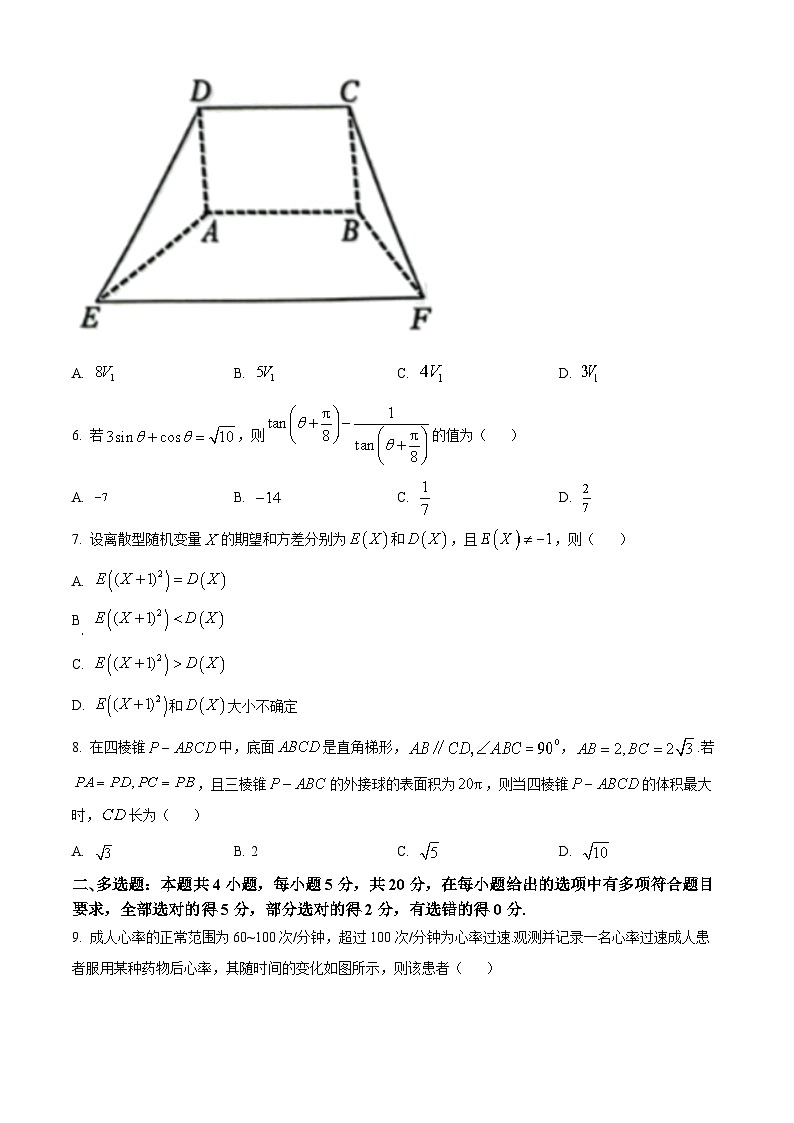
8. 在四棱锥中,底面是直角梯形,,.若,且三棱锥的外接球的表面积为,则当四棱锥的体积最大时,长为( )
A. B. 2 C. D.
二、多选题:本题共4小题,每小题5分,共20分,在每小题给出的选项中有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.
9. 成人心率的正常范围为60~100次/分钟,超过100次/分钟为心率过速.观测并记录一名心率过速成人患者服用某种药物后心率,其随时间的变化如图所示,则该患者( )
A. 服了药物后心率会马上恢复正常
B. 服药后初期药物起效速度会加快
C. 所服药物约15个小时后失效(服药后心率下降期间为有效期)
D. 一天需服用该药1至2次
10. 将函数的图象向左平移个单位长度,再把所得图象上各点的横坐标缩短为原来的,纵坐标保持不变,得到函数的图象,则关于的说法正确的是( )
A. 最小正周期为 B. 偶函数
C. 在上单调递减 D. 关于中心对称
11. 已知函数,其导函数为,则( )
A. 曲线在处的切线方程为
B. 有极大值,也有极小值
C. 使得恒成立的最小正整数为2021
D. 有两个不同零点,且
12. 已知是椭圆上不同的三点,记的面积分别为(为坐标原点).若,则( )
A. B.
C. D. 为定值
非选择题部分
三、填空题:本题共4小题,每小题5分,共20分.
13 已知复数满足,则______.
14. 若的展开式中所有系数绝对值之和为81,则其常数项为______.
15. 已知点在上运动,点在圆上运动,且最小值为,则实数值为______.
16. 已知数列的首项为,且满足,其中为其前项和,若恒有,则的取值范围为______.
四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17. 设等差数列的前项和为,已知.
(1)求数列的通项公式及;
(2)设,求数列的前项和.
18. 记的内角所对的边分别为,已知.
(1)若,求;
(2)若,求的周长.
19. 某型合金钢生产企业为了合金钢的碳含量百分比在规定的值范围内,检验员在同一试验条件下,每天随机抽样10次,并测量其碳含量(单位:%).已知其产品的碳含量服从正态分布.
(1)假设生产状态正常,记表示一天内10次抽样中其碳含量百分比在之外的次数,求及的数学期望:
(2)一天内的抽检中,如果出现了至少1次检测的碳含量在之外,就认为这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.下面是在一天中,检测员进行10次碳含量(单位:%)检测得到的测量结果:
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
碳含量(%) | 0.31 | 0.32 | 0.34 | 0.31 | 0.30 | 0.31 | 0.32 | 0.31 | 0.33 | 0.32 |
经计算得,,其中为抽取的第次的碳含量百分比.
(i)用样本平均数作为估计值,用样本标准差作为的估计值,利用估计值判断是否需对当天的生产过程进行检查?
(ii)若去掉,剩下的数的平均数和标准差分别记为,试写出的算式(用表示).
附:若随机变量服从正态分布,则..
20. 在正三棱台中,侧棱长为1,且为的中点,为上的点,且.
(1)证明:平面,并求出的长;
(2)求平面与平面夹角的余弦值.
21. 设抛物线的焦点为是坐标原点,,过点的直线与抛物线交于两点,延长分别交抛物线于两点,分别是的中点.
(1)求直线的斜率的取值范围;
(2)求的最小值.
22. 设函数.
(1)讨论函数的单调区间;
(2)若对任意,函数均有2个零点,求的取值范围;
相关试卷
这是一份2023-2024学年浙江省浙南名校联盟高一上学期12月联考数学试题(含解析),共18页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
这是一份2024届浙江省浙南名校联盟高三上学期第一次联考数学试题含解析,共23页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
这是一份2024浙江省浙南名校联盟高三上学期第一次联考数学试题含解析,文件包含浙江省浙南名校联盟2023-2024学年高三上学期第一次联考数学试题含解析docx、浙江省浙南名校联盟2023-2024学年高三上学期第一次联考数学试题无答案docx等2份试卷配套教学资源,其中试卷共31页, 欢迎下载使用。












