2022-2023学年北京市清华附中朝阳学校、望京学校高一（上）期中数学试卷(2)

2022-2023学年北京市清华附中朝阳学校、望京学校高一（上）期中数学试卷

一、选择题共10小题，每题4分，共40分，均为单选题．

1．（4分）已知集合A＝{1，2，3，4，5}，B＝{x|﹣1＜x＜3}，则A∩B＝（　　）

A．{1，2，3} B．{x|1＜x＜3} C．{1，2} D．{x|1≤x≤2}

2．（4分）命题“∃x0∈R，”的否定是（　　）

A．∃x0∈R， B．∃x0∈R， 

C．∀x∈R，2x≤0 D．∀x∈R，2x＞0

3．（4分）设a∈R，则“a＞1”是“a2＞a”的（　　）

A．充分不必要条件 B．必要不充分条件 

C．充要条件 D．既不充分也不必要条件

4．（4分）函数y的定义域为（　　）

A．（﹣3，1） B．[1，3] C．[﹣3，1] D．[0，1]

5．（4分）已知函数f（x）＝x|x|﹣2x，则下列结论正确的是（　　）

A．f（x）是偶函数，递增区间是（0，+∞） 

B．f（x）是偶函数，递减区间是（﹣∞，1） 

C．f（x）是奇函数，递减区间是（﹣1，1） 

D．f（x）是奇函数，递增区间是（﹣∞，0）

6．（4分）如果x+y＜0，且y＞0，那么下列不等式成立的是（　　）

A．y2＞x2＞xy B．x2＞y2＞﹣xy C．x2＜﹣xy＜y2 D．x2＞﹣xy＞y2

7．（4分）下列函数中，值域为[0，4]的是（　　）

A．f（x）＝x﹣1，x∈{1，2，3，4，5} B．f（x）＝﹣x2+4 

C．f（x） D．f（x）＝x2（x＞0）

8．（4分）函数y的图象大致为（　　）

A． B． 

C． D．

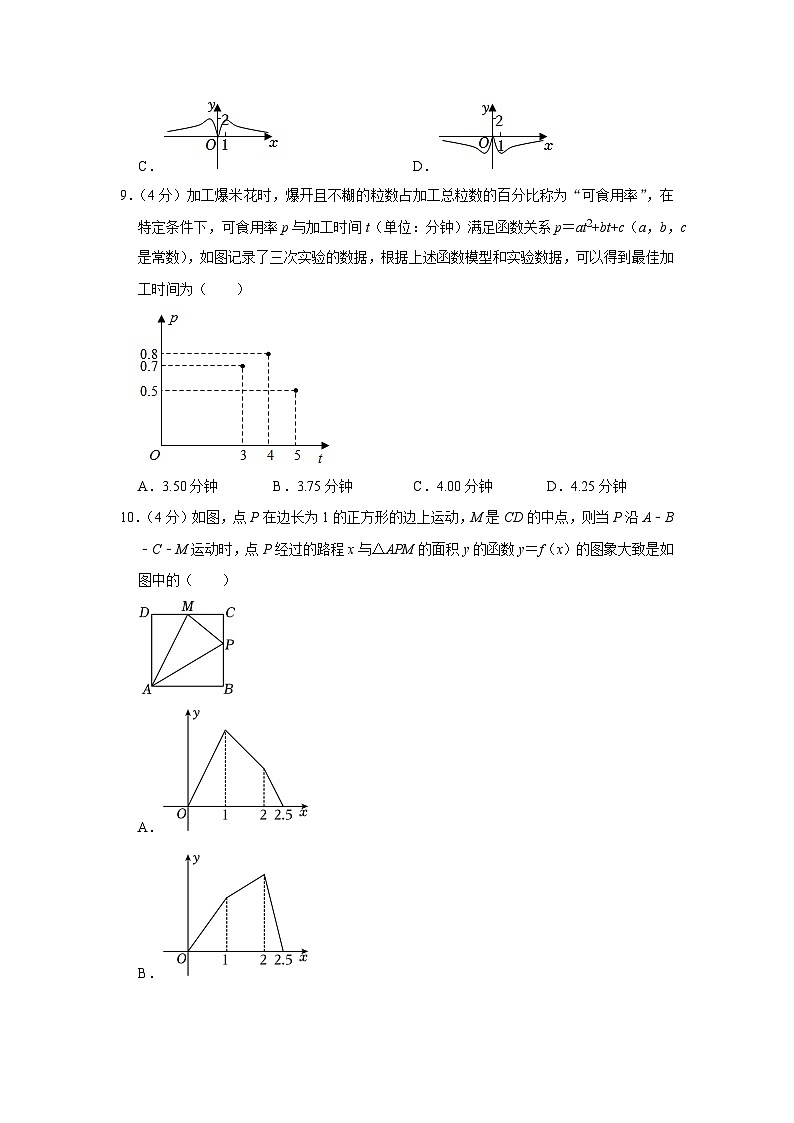
9．（4分）加工爆米花时，爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”，在特定条件下，可食用率p与加工时间t（单位：分钟）满足函数关系p＝at2+bt+c（a，b，c是常数），如图记录了三次实验的数据，根据上述函数模型和实验数据，可以得到最佳加工时间为（　　）

A．3.50分钟 B．3.75分钟 C．4.00分钟 D．4.25分钟

10．（4分）如图，点P在边长为1的正方形的边上运动，M是CD的中点，则当P沿A﹣B﹣C﹣M运动时，点P经过的路程x与△APM的面积y的函数y＝f（x）的图象大致是如图中的（　　）

A． 

B． 

C． 

D．

二、填空题共5小题，每题5分，共25分．

11．（5分）若用列举法表示集合，则A＝　           　．

12．（5分）若幂函数y＝f（x）的图象经过点，则f（4）的值等于 　   　．

13．（5分）已知奇函数f（x），当x＞0时，f（x）＝x2+3x，那么f（﹣2）＝　      　．

14．（5分）已知函数，则不等式f（x2+x+3）＞f（3x2﹣3）的x的解集是 　                  　．

15．（5分）已知偶函数f（x）在[0，+∞）单调递减，若f（﹣2）＝0，则满足xf（x﹣1）＞0的x的取值范围是 　                　．

三、解答题共6小题，共85分，解答应写出文字说明，演算步骤或证明过程．

16．（14分）已知U＝R，A＝{x|2﹣a≤x≤2+a，a＞0}，B＝{x|x2+3x﹣4≤0}．求：

（1）若a＝3，求A∪B，（∁UB）∩A；

（2）若B⊆A，求实数a的取值范围．

17．（14分）解关于x的不等式，并写出解集：

（1）；

（2）ax2﹣2≥2x﹣ax（a∈R）．

18．（14分）已知函数是定义在（﹣2，2）上的奇函数．

（1）确定f（x）的解析式；

（2）用定义证明：f（x）在区间（﹣2，2）上是减函数；

（3）解不等式f（t﹣1）+f（t）＜0．

19．（14分）吉祥物“冰墩墩”在北京2022年冬奥会强势出圈，并衍生出很多不同品类的吉祥物手办．某企业承接了“冰墩墩”玩具手办的生产，已知生产此玩具手办的固定成本为200万元．每生产x万盒，需投入成本h（x）万元，当产量小于或等于50万盒时h（x）＝180x+100；当产量大于50万盒时h（x）＝x2+60x+3500，若每盒玩具手办售价200元，通过市场分析，该企业生产的玩具手办可以全部销售完（利润＝售价﹣成本，成本＝固定成本+生产中投入成本）

（1）求“冰墩墩”玩具手办销售利润y（万元）关于产量x（万盒）的函数关系式；

（2）当产量为多少万盒时，该企业在生产中所获利润最大？

20．（14分）已知函数．

（1）求函数g（x）的解析式；

（2）设，若存在x∈[2，3]使f（x）﹣kx≤0成立，求实数k的取值范围．

21．（15分）定义两个非空数集A，B的“和集”为A+B＝{a+b|a∈A，b∈B}，对有限集合X，记card（X）＝|X|．

（1）已知A＝{1，2，3}，B＝{﹣a|a∈A}，求出A+B与|A+B|；

（2）任取非空有限数集A，B，证明：|A+B|≥|A|+|B|﹣1；

（3）S＝{﹣2022，﹣2021，…，2021，2022}的非空子集T满足：∀a，b，c∈T，都有a+b+c≠0，求|T|max．

2022-2023学年北京市清华附中朝阳学校、望京学校高一（上）期中数学试卷

参考答案与试题解析

一、选择题共10小题，每题4分，共40分，均为单选题．

1．【解答】解：∵A＝{1，2，3，4，5}，B＝{x|﹣1＜x＜3}，

∴A∩B＝{1，2}．

故选：C．

2．【解答】解：因为特称命题的否定是全称命题，

故命题“∃x0∈R，”的否定是∀x∈R，2x＞0．

故选：D．

3．【解答】解：由a2＞a，解得a＜0或a＞1，

故“a＞1”是“a2＞a”的充分不必要条件，

故选：A．

4．【解答】解：由3﹣2x﹣x2＞0，可得﹣3＜x＜1，

所以函数的定义域为（﹣3，1），

故选：A．

5．【解答】解：由函数f（x）＝x|x|﹣2x 可得，函数的定义域为R，且f（﹣x）＝﹣x|﹣x|﹣2（﹣x ）＝﹣x|x|+2x＝﹣f（x），

故函数为奇函数．

函数f（x）＝x|x|﹣2x，如图所示：故函数的递减区间为（﹣1，1），

故选：C．

6．【解答】解：∵x+y＜0，且y＞0，

∴x＜﹣y＜0．

∴x2＞﹣xy，xy＜﹣y2，

因此x2＞﹣xy＞y2．

故选：D．

7．【解答】解：选项A中，f（x）∈{0，1，2，3，4}；选项B中，f（x）∈（﹣∞，4]，

选项C中，由﹣x2≤0，得16﹣x2≤16，则f（x）的值域为[0，4]；

选项D中，f（x）＝x2，f（x）∈[0，+∞）．

故选：C．

8．【解答】解：函数y是奇函数，排除CD，

x＞0时，y＞0，排除B；

故选：A．

9．【解答】解：将（3，0.7），（4，0.8），（5，0.5）分别代入p＝at2+bt+c，可得，

解得a＝﹣0.2，b＝1.5，c＝﹣2，

∴p＝﹣0.2t2+1.5t﹣2，对称轴为t3.75．

故选：B．

10．【解答】解：当点P在AB上时：，

当点P在BC上时：，

当点P在AB上时：，

由函数可知，有三段直线，又当点P在BC上时是减函数，

故选：A．

二、填空题共5小题，每题5分，共25分．

11．【解答】解：由题意得：，则，

∴A＝{（1，﹣1）}，

故答案为：{（1，﹣1）}．

12．【解答】解：设幂函数y＝f（x）＝xα，

∴幂函数y＝f（x）的图象经过点（2，），

∴f（2）＝2α，解得α，

∴f（x），

∴f（4）＝2，

故答案为：2．

13．【解答】解：∵f（x）是奇函数，

∴f（﹣2）＝﹣f（2）＝﹣（4+6）＝﹣10，

故答案为：﹣10．

14．【解答】解：作出函数的图象如图，

由图可知，函数f（x）在R上为增函数，

则f（x2+x+3）＞f（3x2﹣3）⇔x2+x+3＞3x2﹣3，

即2x2﹣x﹣6＜0，解得x＜2．

∴不等式f（x2+x+3）＞f（3x2﹣3）的x的解集是（，2）．

故答案为：（，2）．

15．【解答】解：根据题意，函数f（x）为偶函数，若f（﹣2）＝0，则有f（2）＝0，

若函数f（x）在[0，+∞）单调递减，则在[0，2）上，f（x）＞0，在（2，+∞）上，f（x）＜0，

函数f（x）在（﹣∞，0）上单调递增，则在（﹣∞，﹣2）上，f（x）＜0，在（﹣2，0）上，f（x）＞0，

f（x﹣1）是将函数f（x）的图象向右平移1个单位，其草图如图：

又由xf（x﹣1）＞0，则有或，

解可得x＜﹣1或0＜x＜3；

即x的取值范围为（﹣∞，﹣1）∪（0，3）．

故答案为：（﹣∞，﹣1）∪（0，3）．

三、解答题共6小题，共85分，解答应写出文字说明，演算步骤或证明过程．

16．【解答】解：（1）若a＝3，则A＝{x|﹣1≤x≤5}，B＝{x|﹣4≤x≤1}，

则A∪B＝{x|﹣4≤x≤5}，∁UB＝{x|x＞1或x＜﹣4}，

所以（∁UB）∩A＝{x|1＜x≤5}；

（2）若B⊆A，则且a＞0，解得a≥6，

即实数a的取值范围为[6，+∞）．

17．【解答】解：（1）由得：（5﹣x）（x+3）＞0，解得：﹣3＜x＜5，即不等式的解集为（﹣3，5）．

（2）由ax2﹣2≥2x﹣ax得：ax2+（a﹣2）x﹣2＝（ax﹣2）（x+1）≥0；

①当a＝0时，不等式可化为﹣2x﹣2≥0，解得：x≤﹣1，则不等式解集为（﹣∞，﹣1]；

②当a＞0时，由（ax﹣2）（x+1）≥0得：x≤﹣1或，则不等式解集为；

③当﹣2＜a＜0时，，由（ax﹣2）（x+1）≥0得：，则不等式解集为；

④当a＝﹣2时，，不等式可化为﹣2x2﹣4x﹣2≥0，解得：x＝﹣1，则不等式解集为{﹣1}；

⑤当a＜﹣2时，，由（ax﹣2）（x+1）≥0得：，则不等式解集为；

综上所述：当a＝0时，不等式解集为（﹣∞，﹣1]；

当a＞0时，不等式解集为；

当﹣2＜a＜0时，不等式解集为；

当a＝﹣2时，不等式解集为{﹣1}；

当a＜﹣2时，不等式解集为．

18．【解答】解：（1）由奇函数的性质得，f（0）0，

故m＝0，f（x），

证明：（2）设﹣2＜x1＜x2＜2，

则f（x1）﹣f（x2）0，

所以f（x1）＞f（x2），

故f（x）在区间（﹣2，2）上是减函数；

（3）因为f（x）在区间（﹣2，2）上是减函数且为奇函数，

由f（t﹣1）+f（t）＜0得f（t﹣1）＜﹣f（t）＝f（﹣t），

所以2＞t﹣1＞﹣t＞﹣2，

解得，，

故不等式的解集（，2）．

19．【解答】解：（1）当产量小于或等于50万盒时，y＝200x﹣200﹣180x﹣100＝20x﹣300，

当产量大于50万盒时，y＝200x﹣200﹣x2﹣60x﹣3500＝﹣x2+140x﹣3700，

故，

（2）当0≤x≤50时，y≤20×50﹣300＝700，

当x＞50时，y＝﹣x2+140x﹣3700，

当时，y＝﹣x2+140x﹣3700取到最大值，为1200，

因为700＜1200，所以当产量为70万盒时，该企业所获利润最大．

20．【解答】解：（1）解法一：∵，∴g（x）＝（x﹣1）2．

又，∴g（x）＝（x﹣1）2（x≥2）．

解法二：令，则x＝（t﹣2）2．由于，所以t≥2．

代入原式有g（t）＝（t﹣2）2+2（t﹣2）+1＝（t﹣1）2，

所以g（x）＝（x﹣1）2（x≥2）．

（2）∵，∴．

∵存在x∈[2，3]使f（x）﹣kx≤0成立，

∴在x∈[2，3]时有解．

令，由x∈[2，3]，得，

设h（t）＝t2﹣4t+1＝（t﹣2）2﹣3．

则函数h（t）的图象的对称轴方程为t＝2，

∴当时，函数h（t）取得最小值．

∴k，即k的取值范围为[，+∞）．

21．【解答】解：（1）∵B＝{﹣a|a∈A}＝{﹣3，﹣2，﹣1}，∴A+B＝{﹣2，﹣1，0，1，2}，∴|A+B|＝5．

（2）证明：设A＝{a1，a2，a3，⋅⋅⋅，an}，B＝{b1，b2，b3，⋅⋅⋅，bm}，

则当|A+B|最小时，A+B＝{a1+b1，a1+b2，a1+b3，⋅⋅⋅，a1+bm，a2+bm，a3+bm，⋅⋅⋅，an+bm}，∴|A+B|min＝m+n﹣1，又|A|＝n，|B|＝m，∴|A+B|≥m+n﹣1＝|A|+|B|﹣1．

（3）∵∀a，b，c∈T，都有a+b+c≠0，

若0∈T，则a≠﹣b，若|T|最大，则T＝{﹣2022，﹣2021，⋅⋅⋅，﹣1，0}或T＝{0，1，2，⋅⋅⋅，2021，2022}，∴|T|max＝2023；

若0∉T，若a∈[﹣2022，﹣1]且a∈Z，则﹣（b+c）∉T，∴|T|≤2022，

综上所述：|T|max＝2023．

26 11:08:01