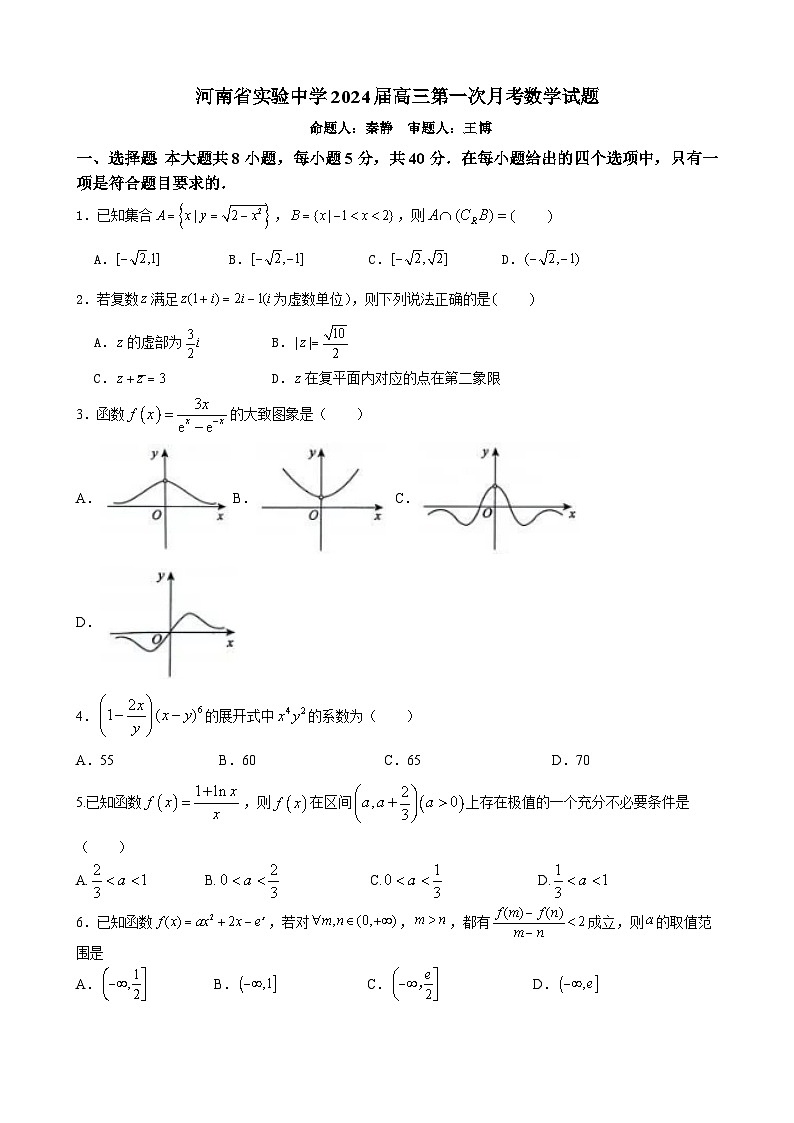
河南省实验中学2024届高三第一次月考数学试题及参考答案

河南省实验中学2024届高三第一次月考数学试题（9月26号）

                             参考答案：

一、选择题

1---4  BBAA   5---8 ACDC   9. BD      10.  AC        11. ABD   12.ACD

二、填空题

13. 0.024    14.    15.     16．

三、解答题

17.（10分）解：（1）

，又因为，

所以是首项为2，公比为2的等比数列。.......4分

（2）

满足上式.    .......7分

.......10分

18．（12分）解：（1）证明：由题意得，即，由正弦定理得，

由余弦定理知，，，，

，，

又是锐角三角形，，；.......5分

（2）在中，由正弦定理得，，

是锐角三角形，且；

，解得，.......8分

，，

线段长度的取值范围为，．.......12分

19.（12分）解：作于点，于点，

因为，，则，，

所以，又，所以，.......2分

由余弦定理可知，得到，所以，

所以，又底面，面，

所以，又，面，所以平面，

又面,所以........6分

（2）以点为原点，为轴，为轴，为轴，建立如图坐标系

因为平面，所以与平面所成的角就是

所以，为等腰直角三角形，所以

，，，，

设平面的法向量，则则由，得到，

取，得，

又易知，平面的一个法向量，

，由图知二面角为锐角

所以二面角的余弦值为........12分

20.（12分）（1）解：由勾股定理可得，其中，所以，，其中.……6分

（2）解：，

由可得；由可得.

所以，函数在上单调递减，在上单调递增，……10分

故当时，函数取最小值，即

（万元），因此，当公里时，总费用最小，且最小费用为3680万元.……12分

21.（12分）解：（1）由 ，得，设中位数为，由 ，解得，由频率分布直方图可知众数为65........3分

（2）从这1000人问卷调查得到的平均值为

因为由于得分服从正态分布，

所以 ........6分

（3）设得分不低于分的概率为，则，

的取值为10，20，30，40，

，，

，，

所以的分布列为：

所以........12分

22.（12分）（1）依题意，得.

当时，，所以在单调递增.

当时，令，可得；

令，可得，

所以在单调递增，在单调递减.

综上所述，当时，在单调递增；当时，在单调递增，在单调递减........5分

（2）因为当时，，所以，

即，

即，

即........7分

令，则有对恒成立.

因为，所以在单调递增，         

故只需，

即对恒成立........9分

令，则，令，得.

当时，，当时，，

所以在单调递增，在单调递减，

所以.  因此，所以........12分