中考数学专项训练（25）专题　模型　隐圆模型－－－－－米勒定理（最大张角问题）含解析答案

中考数学专项训练（25）专题 　模型　隐圆模型－－－－－米勒定理（最大张角问题）

学校:___________姓名：___________班级：___________考号：___________

一、单选题

1．如图，在矩形ABCD中，AB=4，BC=6，E是矩形内部的一个动点，且AE⊥BE，则线段CE的最小值为（　　）

A． B．2﹣2 C．2﹣2 D．4

2．在平面直角坐标系中，A，B，C，点P为任意一点，已知PA⊥PB，则线段PC的最大值为（    ）

A．3 B．5 C．8 D．10

3．如图，△ABC中，AB＝AC＝2，BC＝2，D点是△ABC所在平面上的一个动点，且∠BDC＝60°，则△DBC面积的最大值是(   )

A．3 B．3 C． D．2

4．如图，是的直径，、是弧（异于、）上两点，是弧上一动点，的角平分线交于点，的平分线交于点．当点从点运动到点时，则、两点的运动路径长的比是（    ）

A． B． C． D．

二、填空题

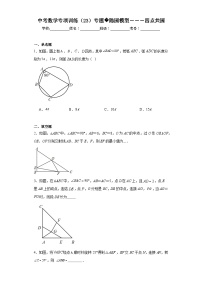
5．已知正方形ABCD边长为2，E、F分别是BC、CD上的动点，且满足，连接AE、BF， 交点为P点，则PD的最小值为         ．

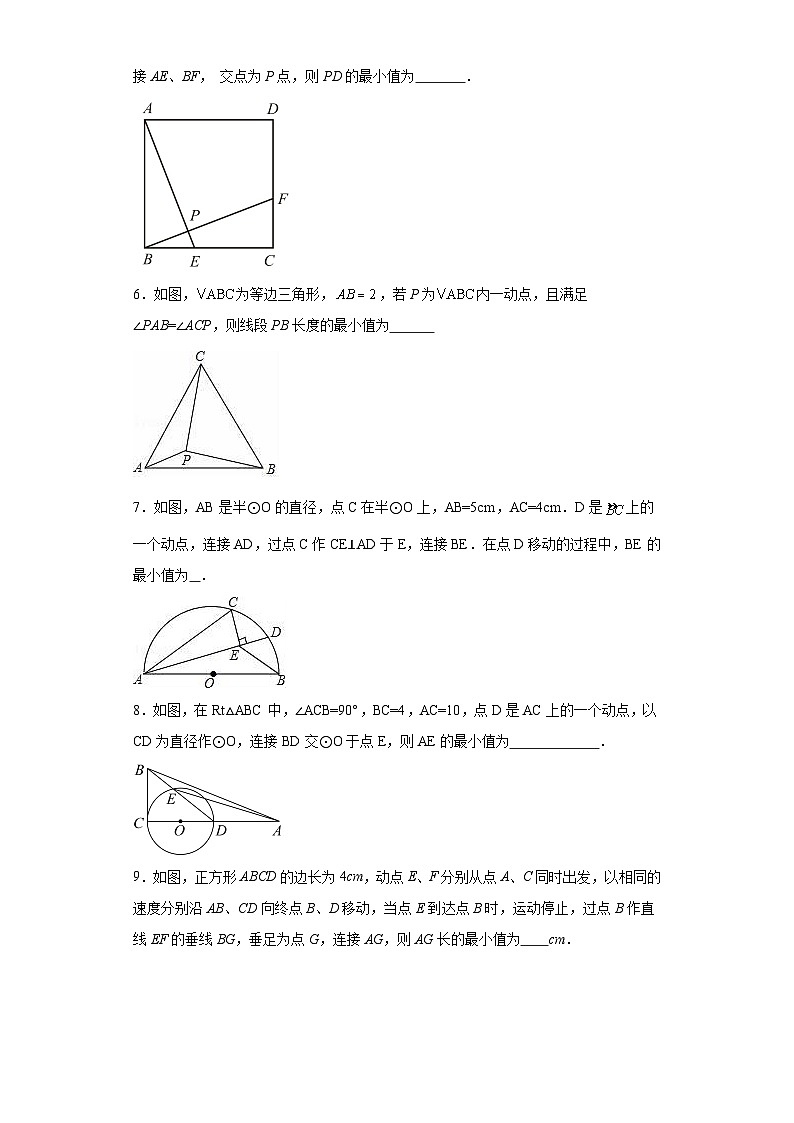
6．如图，为等边三角形，，若P为内一动点，且满足∠PAB=∠ACP，则线段PB长度的最小值为       

7．如图，AB是半⊙O的直径，点C在半⊙O上，AB=5cm，AC=4cm．D是上的一个动点，连接AD，过点C作CE⊥AD于E，连接BE．在点D移动的过程中，BE的最小值为  ．

8．如图，在Rt△ABC中，∠ACB=90°，BC=4，AC=10，点D是AC上的一个动点，以CD为直径作⊙O，连接BD交⊙O于点E，则AE的最小值为                ．

9．如图，正方形ABCD的边长为4cm，动点E、F分别从点A、C同时出发，以相同的速度分别沿AB、CD向终点B、D移动，当点E到达点B时，运动停止，过点B作直线EF的垂线BG，垂足为点G，连接AG，则AG长的最小值为     cm．

三、解答题

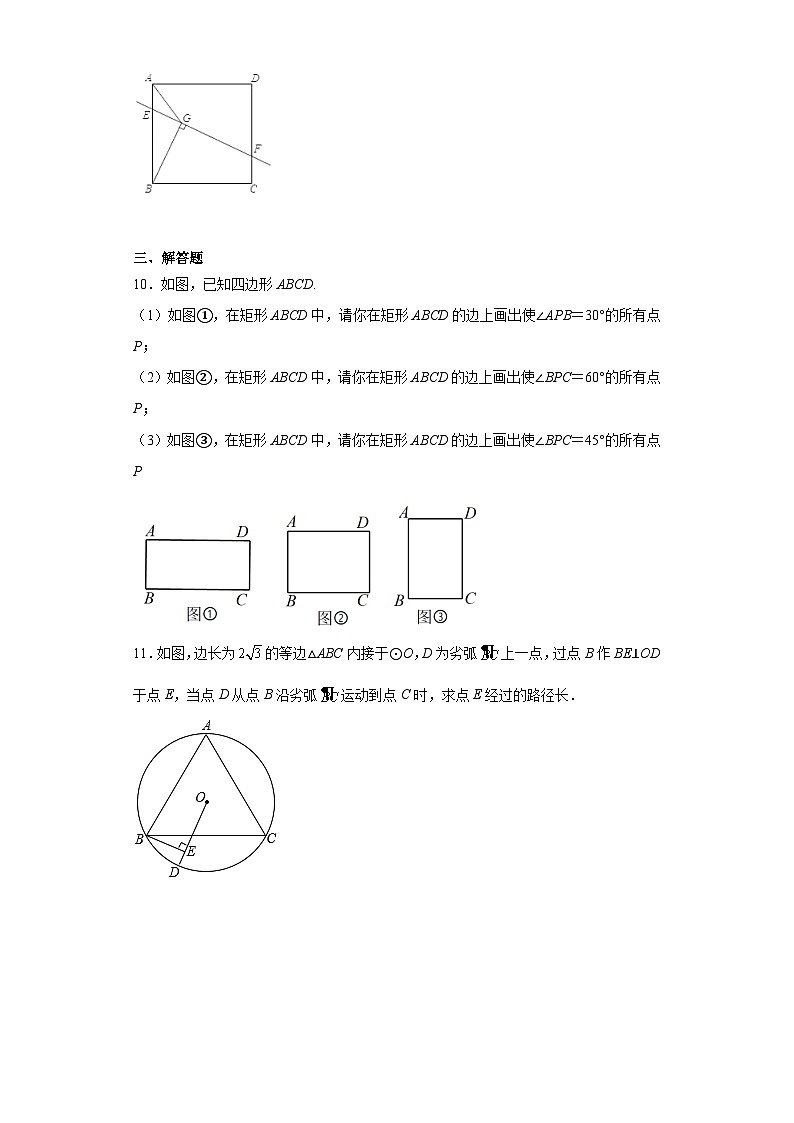
10．如图，已知四边形ABCD.

（1）如图①，在矩形ABCD中，请你在矩形ABCD的边上画出使∠APB＝30°的所有点P；

（2）如图②，在矩形ABCD中，请你在矩形ABCD的边上画出使∠BPC＝60°的所有点P；

（3）如图③，在矩形ABCD中，请你在矩形ABCD的边上画出使∠BPC＝45°的所有点P

11．如图，边长为的等边△ABC内接于⊙O，D为劣弧上一点，过点B作BE⊥OD于点E，当点D从点B沿劣弧运动到点C时，求点E经过的路径长．

参考答案：

1．B

【详解】解：如图，

∵AE⊥BE，

∴点E在以AB为直径的半⊙O上，

连接CO交⊙O于点E′，

∴当点E位于点E′位置时，线段CE取得最小值，

∵AB=4，

∴OA=OB=OE′=2，

∵BC=6，

∴OC=，

则CE′=OC﹣OE′=﹣2，

故选B．

【点睛】主要考查圆周角定理、圆的基本性质及矩形的性质、勾股定理，根据AE⊥BE知点E在以AB为直径的半⊙O上是解题的关键．

2．C

【分析】连接OC、OP、PC由PA⊥PB可得点P在以O为圆心，AB长为直径的圆上；再根据三角形的三边关系可得CP≤OP+OC，则当当点P，O，C在同一直线上， CP的最大值为OP+OC的长，然后进行计算即可.

【详解】解：如图所示，连接OC、OP、PC

∵PA⊥PB，

∴点P在以O为圆心，AB长为直径的圆上，

∵△COP

∴CP≤OP+OC，

∴当点P，O，C在同一直线上，且点P在CO延长线上时，CP的最大值为OP+OC的长，

又∵A（-3，0），B（3，0），C（3，4），

∴AB=6，OC=5，OP=AB=3，

∴线段PC的最大值为OP+OC=3+5=8，

故答案为C．

【点睛】本题考查了90°所对的弦为圆的直径、三角形的三边关系以及最短路径问题，其中确定最短路径是解答本题的关键.

3．A

【分析】因为AB＝AC＝2，BC＝2，可得∠BAC＝120°，以A为圆心，AB为半径作⊙A，与HA的延长线相交于点D，因为∠BDC＝60°，所以点D在⊙O上运动，当D运动到如图的位置时，△DBC面积最大，根据三角形面积公式即可得出△DBC面积的最大值．

【详解】解：如图，作AH⊥BC于H，

∵AB＝AC＝2，BC＝2，

∴BH＝BC＝，

∴AH＝=1，

∴sin∠ABC＝=，

∴∠ABC＝∠ACB＝30°，∠BAC＝120°，

以A为圆心，AB为半径作⊙A，延长HA交⊙A于点D，

∵∠BDC＝60°，

∴点D在⊙O上运动，当D运动到如图的位置时，△DBC面积的最大值，最大值为：．

故选A．

【点睛】本题考查等腰三角形的性质，圆周角定理，勾股定理．解题的关键是得出点D在⊙A上运动．

4．A

【分析】连接BE，由题意可得点E是△ABC的内心，由此可得∠AEB＝135°，为定值，确定出点E的运动轨迹是是弓形AB上的圆弧，此圆弧所在圆的圆心在AB的中垂线上，根据题意过圆心O作直径CD，则CD⊥AB，在CD的延长线上，作DF＝DA，则可判定A、E、B、F四点共圆，继而得出DE＝DA＝DF，点D为弓形AB所在圆的圆心，设⊙O的半径为R，求出点C的运动路径长为，DA＝R，进而求出点E的运动路径为弧AEB，弧长为，即可求得答案.

【详解】连结BE，

∵点E是∠ACB与∠CAB的交点，

∴点E是△ABC的内心，

∴BE平分∠ABC，

∵AB为直径，

∴∠ACB＝90°，

∴∠AEB＝180°－(∠CAB+∠CBA)＝135°，为定值，，

∴点E的轨迹是弓形AB上的圆弧，

∴此圆弧的圆心一定在弦AB的中垂线上，

∵，

∴AD=BD，

如下图，过圆心O作直径CD，则CD⊥AB，

∠BDO＝∠ADO＝45°，

在CD的延长线上，作DF＝DA，

则∠AFB＝45°，

即∠AFB+∠AEB＝180°，

∴A、E、B、F四点共圆，

∴∠DAE＝∠DEA＝67.5°，

∴DE＝DA＝DF，

∴点D为弓形AB所在圆的圆心，

设⊙O的半径为R，

则点C的运动路径长为：，

DA＝R，

点E的运动路径为弧AEB，弧长为：，

C、E两点的运动路径长比为：，

故选A.

【点睛】本题考查了点的运动路径，涉及了三角形的内心，圆周角定理，四点共圆，弧长公式等，综合性较强，正确分析出点E运动的路径是解题的关键.

5．

【分析】根据正方形的性质及已知条件可证≅，由全等三角形的性质及等量代换得出，所以可得点P在以AB为直径的圆上，当点P、点D和点O三点在一条直线上时，此时即为PD的最小值，根据图形运用勾股定理计算OD，再根据圆的性质计算出圆的半径OP，即可得到答案．

【详解】解：如图所示：

在正方形ABCD中，，，

在和中，

，

∴≅，

∴，

∵，

∴，

即，

∴，

根据圆周角定理，作一个以AB为直径的圆O，角所对的弦是直径，

∴点P在以AB为直径的圆O上，如图所示：

∵P圆上的动点，

∴当点P、点D和点O不在一条直线时，根据三角形的性质可得，

当点P、点D和点O三点在一条直线上时，，

∴当点P、点D和点O三点在一条直线上时，此时即为PD的最小值，

在中，，

∴，

∵，

∴

故答案为：．

【点睛】题目主要考查圆周角定理、全等三角形的判定和性质、勾股定理等知识点，熟练掌握圆周角定理作出相应辅助线是解题关键．

6．

【详解】解：∵△ABC是等边三角形，

∴∠ABC=∠BAC=60°，AC=AB=2，

∵∠PAB=∠ACP，

∴∠PAC+∠ACP=60°，

∴∠APC=120°，

∴点P的运动轨迹是，

当O、P、B共线时，PB长度最小，设OB交AC于D，如图所示：

此时PA=PC，OB⊥AC，

则AD=CD=AC=1，∠PAC=∠ACP=30°，∠ABD=∠ABC=30°，

∴，

∴，

故答案为：．

7．﹣2

【分析】如图，取AC的中点为O'，连接BO′、BC．在点D移动的过程中，点E在以AC为直径的圆上运动，当O′、E、B共线时，BE的值最小，最小值为O′B﹣O′E，利用勾股定理求出BO′即可解决问题．

【详解】解：如图，取AC的中点为O'，连接BO′、BC．

∵CE⊥AD，

∴∠AEC＝90°，

∴在点D移动的过程中，点E在以AC为直径的圆上运动，

∵AB是直径，

∴∠ACB＝90°，

在Rt△ABC中，∵AC＝4cm，AB＝5cm，

∴BC3cm，

在Rt△BCO′中，BO′cm，

∵O′E+BE≥O′B，

∴当O′、E、B共线时，BE的值最小，最小值为O′B﹣O′E2（cm），

故答案为：（）cm．

【点睛】本题考查勾股定理、点与圆的位置关系等知识，解题的关键是确定点E的运动轨迹是以AC为直径的圆上运动，属于中考填空题中 压轴题．

8．

【分析】连接CE，可得∠CED＝∠CEB＝90°，从而知点E在以BC为直径的⊙Q上，继而知点Q、E、A共线时AE最小，根据勾股定理求得QA的长，即可得答案．

【详解】解：如图，连接CE，

∴∠CED＝∠CEB＝90°，

∴点E在以BC为直径的⊙Q上，

∵BC＝4，

∴QC＝QE＝2，

当点Q、E、A共线时AE最小，

∵AC＝10，

∴AQ＝=，

∴AE＝AQ−QE＝，

∴AE的最小值为，

故答案为．

【点睛】本题考查了圆周角定理和勾股定理，解决本题的关键是确定E点运动的规律，从而把问题转化为圆外一点到圆上一点的最短距离问题．

9．.

【分析】根据正方形的性质得出当E，F运动到AB，CD的中点时，AG最小解答即可．

【详解】解：设正方形的中心为O，可证EF经过O点．

连结OB，取OB中点M，连结 MA，MG，则MA，MG为定长，

可计算得，

当A，M，G三点共线时，AG最小＝cm，

故答案为

【点睛】本题主要考查了正方形的性质，根据正方形的性质得出当E，F运动到AB，CD的中点时，AG最小是解决本题的关键．

10．（1）见解析；（2）见解析；（3）见解析

【分析】（1）如图①，先作等边三角形，再以点为圆心，为半径作，则与矩形的边，的交点，即是使的所有点；

（2）如图②，先作等边三角形，再画的外接圆，则与矩形的边，，的交点，，，即是使的所有点；

（3）如图③，先作等腰直角三角形，其中，再以点为圆心，为半径作，则与矩形的边，的交点，即是使的所有点．

【详解】（1）

如图①所示，点，即是使的所有点；

（2）

如图②所示，点，，，即是使的所有点；

（3）

如图③所示，点，即是使的所有点．

【点睛】本题考查轨迹、等边三角形与等腰直角三角形的性质、三角形的外接圆与外心等知识，解题的关键是学会添加常用辅助线，正确寻找轨迹．

11．

【分析】如图，以OB为直径画⊙K交AB于T，连接TK，图中的优弧，即为点E的运动轨迹．求出圆心角，半径即可解决问题．

【详解】

如图，以OB为直径画⊙K交AB于T，连接TK，图中的优弧，即为点E的运动轨迹．

∵△ABC是等边三角形，

∴∠OBA=∠OBC=30°，

∴∠TKO=60°，

∵AB=BC=AC=，

∴OB=2，

∴KO=1，

∴点E经过的路径长为．

【点睛】本题考查轨迹、等边三角形的性质、弧长公式、三角形的外接圆与外心等知识，解题的关键是学会添加常用辅助线，正确寻找轨迹．