高中北师大版 (2019)5 正态分布课文ppt课件

这是一份高中北师大版 (2019)5 正态分布课文ppt课件，共40页。PPT课件主要包含了目录索引，正态分布，正态曲线，误差模型，本节要点归纳等内容，欢迎下载使用。

基础落实·必备知识全过关
重难探究·能力素养全提升
成果验收·课堂达标检测
知识点1　正态分布的概念及特点1.概念 　　　　 　 与之前学过的离散型随机变量区分由误差引起的连续型随机变量其分布密度函数图象如图所示,对应的分布密度函数解析式为φμ, ,x∈(-∞,+∞),其中实数μ,σ(σ>0)为参数,这一类随机变量X的分布密度(函数)称为正态分布密度(函数),简称　　　　　　　　,对应的图象为正态分布密度曲线,简称　　　　　　. 
正态分布是最常见、最重要的连续型随机变量的分布,是刻画误差分布的重要模型,因此也称为　　　　　　　　. 如果随机变量X服从正态分布,记为　　　　　　　　　,其中EX=　　　,DX=　　　. 
X~N(μ,σ2)　
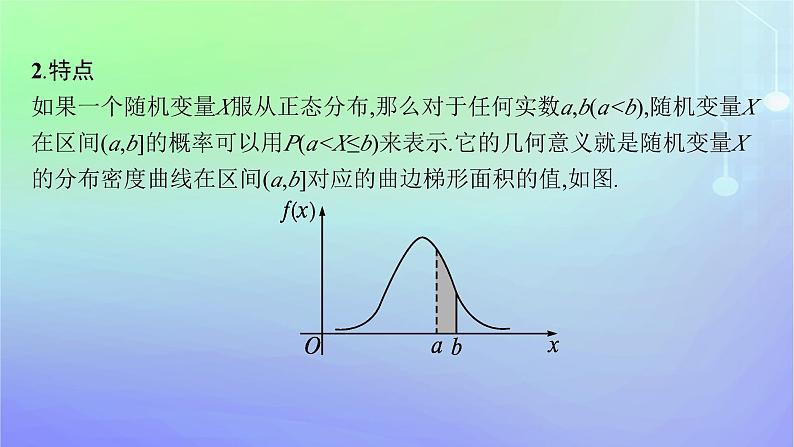
2.特点如果一个随机变量X服从正态分布,那么对于任何实数a,b(a过关自诊1.判断正误.(正确的画√,错误的画×)(1)正态分布是对连续型随机变量而言的.(　　)(2)正态分布密度函数中的参数μ和σ的意义分别是样本的均值和方差.(　　)
2.正态分布函数中的μ,σ的含义是什么?
提示 若X~N(μ,σ2),则EX=μ,DX=σ2,其中μ反映随机变量取值的平均水平,σ衡量随机变量总体波动大小.
3.[人教A版教材习题]举出两个服从正态分布的随机变量的例子.
提示 答案不唯一.(1)某地区16岁男孩的身高分布可以近似看成服从正态分布;(2)某年某地区考生的高考成绩的分布近似看成服从正态分布.
知识点2　正态曲线的性质正态曲线有如下性质:(1)曲线在x轴的上方,与x轴不相交.(2)曲线是单峰的,关于直线x=μ对称.(3)曲线的最高点位于x=μ处.(4)当x<μ时,曲线上升;当x>μ时,曲线下降;并且当曲线向左、右两边无限延伸时,以x轴为渐近线(如图).
因为正态分布完全由μ和σ确定,所以正态曲线还具有下列特点:(1)当σ一定时,曲线的位置由μ确定,曲线随着μ的变化而沿x轴平移.(2)当μ一定时,曲线的形状由σ确定.σ越大,曲线越“矮胖”,表示总体的分布越分散;σ越小,曲线越“高瘦”,表示总体的分布越集中.
过关自诊1.判断正误.(正确的画√,错误的画×)(1)正态曲线是一条钟形曲线.(　　)(2)正态曲线是单峰的,其与x轴围成的面积是随参数μ,σ的变化而变化的.(　　)(3)正态曲线可以关于y轴对称.(　　)
3.[人教A版教材习题]设随机变量X~N(0,22),随机变量Y~N(0,32),画出正态分布密度曲线草图,并指出P(X≤-2)与P(X≤2)的关系,以及P(|X|≤1)与P(|Y|≤1)之间的大小关系.
提示 正态分布密度曲线草图如图所示.∵X~N(0,22),∴P(X≤-2)=P(X≥2),∴P(X≤2)=1-P(X≥2)=1-P(X≤-2),∴P(X≤-2)+P(X≤2)=1.由图易知P(|X|>1)1),且P(|X|≤1)=1-P(|X|>1),P(|Y|≤1)=1-P(|Y|>1),故1-P(|X|>1)>1-P(|Y|>1),即P(|X|≤1)>P(|Y|≤1).
知识点3　正态分布的随机变量在三个特殊区间内取值的概率值及3σ原则1.三个常用概率值如图,正态分布随机变量X在区间(μ-σ,μ+σ](σ>0)上取值的概率为阴影部分的面积.特别地,P(μ-σ2.3σ原则随机变量X在区间(μ-3σ,μ+3σ]外取值的概率只有0.3%,通常认为这种情况在一次试验中几乎是不可能发生的,认为是小概率事件.因此,在实际应用中,通常认为服从正态分布N(μ,σ2)的随机变量X只取区间(μ-3σ,μ+3σ]之间的值,并称之为3σ原则.
名师点睛对小概率事件的正确理解(1)小概率事件是针对“一次试验”来说的,如果试验次数多了,该事件当然是很有可能发生的;(2)当我们运用“小概率事件几乎不可能发生”的原理进行推断时,也有0.3%犯错的可能.
过关自诊1.[人教A版教材习题]某市高二年级男生的身高X(单位:cm)近似服从正态分布N(170,52),随机选择一名本市高二年级的男生,求下列事件的概率:(1)165175.
提示 ∵X~N(170,52),∴μ=170,σ=5.∴(1)P(165175)=P(X≤165)≈0.158 7.
2.[人教A版教材习题]若X~N(μ,σ2),则X位于区域[μ,μ+σ]内的概率是多少?
3.[人教A版教材习题]袋装食盐标准质量为400 g,规定误差的绝对值不超过4 g就认为合格.假设误差服从正态分布,随机抽取100袋食盐,误差的样本均值为0,样本方差为4.请你估计这批袋装食盐的合格率.
提示 设误差为X,由题意得X~N(0,4),∴μ=0,σ=2,∴P(-4≤X≤4)≈0.954 4.因此估计这批袋装食盐的合格率为95.44% .
探究点一　　正态分布的概念及正态曲线的性质
【例1】 如图所示是一个正态曲线,试根据该图象写出其正态分布的密度函数的解析式,求出随机变量的期望和方差.
规律方法　利用正态曲线的性质可以求参数μ,σ,具体方法如下:(1)正态曲线是单峰的,它关于直线x=μ对称,由此性质结合图象求μ.(2)正态曲线在x=μ处达到峰值 ,由此性质结合图象可求σ.
A.σ1>σ2>σ3B.σ3>σ2>σ1C.σ1>σ3>σ2D.σ2>σ1>σ3
解析 由σ的意义可知,图象越“高瘦”,数据越集中,σ2越小,故有σ1>σ2>σ3.
探究点二　　服从正态分布的变量的概率问题
【例2】 (1)已知随机变量ξ服从正态分布N(2,σ2),且P(ξ<4)=0.8,则P(0<ξ≤2)=(　　)A.0.6B.0.4C.0.3D.0.2
解析 ∵随机变量X服从正态分布N(2,σ2),∴μ=2,对称轴是直线x=2.∵P(ξ<4)=0.8,∴P(ξ≥4)=P(ξ≤0)=0.2,∴P(0<ξ≤4)=0.6,∴P(0<ξ≤2)=0.3.故选C.
(2)在某项测量中,测量结果服从正态分布N(1,4),求正态总体X在(-1,1]内取值的概率.
解 由题意得μ=1,σ=2,所以P(-1规律方法　利用正态分布求概率的两个方法
变式训练2设随机变量X~N(2,9),若P(X>c+1)=P(X解 (1)由X~N(2,9)可知,正态分布密度函数关于直线x=2对称(如图所示),又P(X>c+1)=P(X探究点三　　正态分布的实际应用
【例3】 设在一次数学考试中,某班学生的分数X~N(110,202),且知试卷满分150分,这个班的学生共54人,估计这个班在这次数学考试中及格(即90分及以上)的人数和130分及以上的人数.
∴P(X≥90)≈1-0.158 7=0.841 3.∴54×0.841 3≈45(人),即及格人数约为45人.∴54×0.158 7≈8(人),即130分以上的人数约为8人.
规律方法　1.本题利用转化的思想方法,把普通的区间转化为3σ区间,由特殊区间的概率值求出.2.解答正态分布的实际应用题,其关键是如何转化,同时应熟练掌握正态分布在(μ-σ,μ+σ],(μ-2σ,μ+2σ],(μ-3σ,μ+3σ]三个区间内的概率.在此过程中用到归纳思想和数形结合思想.
变式训练3某地高三学生有15 000名,在一次调研测试中,数学成绩ξ服从正态分布N(100,σ2),已知P(80<ξ<120)=0.70,若以按成绩分层随机抽样的方式取100份试卷进行分析,则应从120分以上的试卷中抽取　　　份. 
解析 根据正态分布N(100,σ2),μ=100,P(80<ξ<120)=0.7,所以根据分层随机抽样,可得120分以上抽取份数为100×0.15=15.
1.知识清单:(1)正态分布的概念及特点.(2)正态曲线的性质.(3)三个特殊区间的概率值及3σ原则.2.核心素养:直观想象、数学建模.3.常见误区:(1)不能正确理解μ和σ的意义;(2)不能正确地利用正态曲线求区间上的概率.
A.μ1<μ2,σ1<σ2B.μ1<μ2,σ1>σ2C.μ1>μ2,σ1<σ2D.μ1>μ2,σ1>σ2
3.已知随机变量X服从正态分布N(3,1),且P(24)=(　　) 8 6 5
解析 P(34)=0.5-P(34.若随机变量X~N(μ,σ2),则P(X≤μ)=　　　　.