

中考方差专项训练
展开中考方差专项训练
学校:___________姓名:___________班级:___________考号:___________
| 一、单选题 |
1.一组数据:3,4,4,5,4,6,2,4,4,4,则其平均数和方差分别是( )
A.4,10 B.4,1 C.10,4 D.1,4
2.某校举行年度十佳校园歌手大赛,林老师根据七位评委所给的分数,把最后一位参赛同学的得分制作成如下表格,对七位评委所给的分数,如果去掉一个最高分和一个最低分,那么表中数据一定不会发生变化的是( )
平均数 | 中位数 | 众数 | 方差 |
分 | 分 | 分 |
A.平均数 B.中位数 C.众数 D.方差
3.为了倡导节约用水,某家庭记录了去年12个月的月用水量如下表(且为整数).下列关于用水量的统计量中,不会发生变化的是( )
用水量x/吨 | 3 | 4 | 5 | 6 | 7 |
频数 | 1 | 2 | 5 | a |
A.平均数、中位数 B.众数、中位数 C.平均数、方差 D.众数、方差
4.小颖对数据进行统计分析,发现“”的个位数字被墨水涂污看不到了,下列统计量中不受此影响的是( )
A.中位数 B.平均数 C.众数 D.方差
5.一位卖“运动鞋”的经销商到一所学校对9位学生的鞋号进行了抽样调查.经销商最感兴趣的是这组数据中的( )
A.众数 B.中位数 C.平均数 D.方差
6.一组数据:5,5,3,x,6,2的平均数为4,则这组数据的方差为( )
A.1 B.2 C.3 D.4
7.一组数据6,5,4,5,1,3,对该组数据描述错误的是( )
A.平均数是4 B.中位数是 C.众数是5 D.方差是3
8.小红同学为了在明年中考体育考试中取得好的成绩,每天自己在家里练习做一分钟仰卧起坐,妈妈统计了她一个星期内做仰卧起坐的个数:30、28、25、30、27、30、26.则下列关于小红同学一个星期做仰卧起坐的个数的中位数、众数、平均数和方差分说法不正确的是( )
A.中位数是30 B.众数是30 C.平均数是28 D.方差是
9.某排球队6名场上队员的身高(单位:)是:180,184,188,190,192,194,现用一名身高为的队员换下场上身高为的队员,与换人前相比,场上队员的身高( )
A.平均数变小,方差变小 B.平均数变小,方差不变
C.平均数变大,方差变小 D.平均数变大,方差不变
10.一组数据2,2,2,3,5,8,13,若加入一个数,一定不会发生变化的统计量是( )
A.方差 B.平均数 C.中位数 D.众数
| 二、解答题 |
11.甲、乙两名运动员参加射击训练,将他们的成绩分别制成如下两个统计图:
根据以上信息,整理分析数据如下:
| 平均成绩 | 中位数 | 众数 | 方差 |
甲 | 7 | b | c | 4.2 |
乙 | a | 7 | 8 | d |
(1)填空:表格中__________, __________, __________, __________;
(2)通过上表中的统计量,分析这两名运动员的射击训练成绩,若要选派其中一名运动员参加市射击比赛,你认为应选派谁?
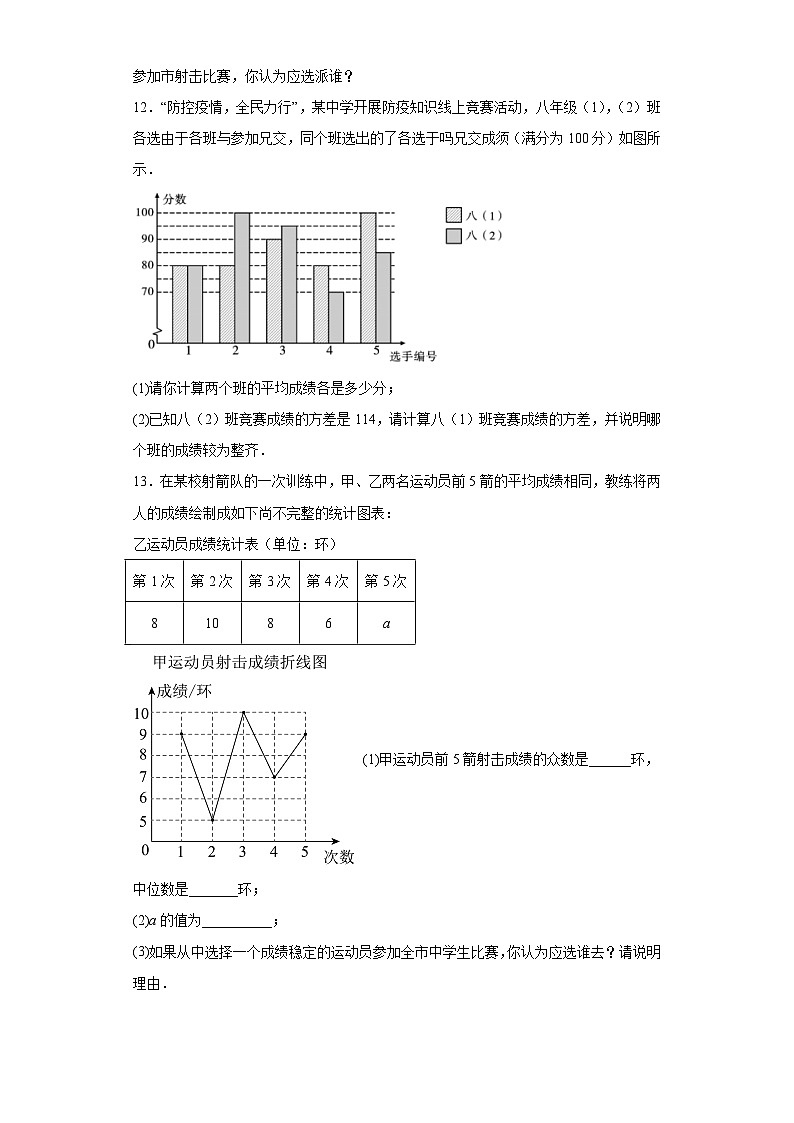
12.“防控疫情,全民力行”,某中学开展防疫知识线上竞赛活动,八年级(1),(2)班各选由于各班与参加兄交,同个班选出的了各选于吗兄交成须(满分为100分)如图所示.
(1)请你计算两个班的平均成绩各是多少分;
(2)已知八(2)班竞赛成绩的方差是114,请计算八(1)班竞赛成绩的方差,并说明哪个班的成绩较为整齐.
13.在某校射箭队的一次训练中,甲、乙两名运动员前5箭的平均成绩相同,教练将两人的成绩绘制成如下尚不完整的统计图表:
乙运动员成绩统计表(单位:环)
第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
8 | 10 | 8 | 6 | a |
(1)甲运动员前5箭射击成绩的众数是______环,中位数是_______环;
(2)a的值为__________;
(3)如果从中选择一个成绩稳定的运动员参加全市中学生比赛,你认为应选谁去?请说明理由.
| 三、填空题 |
14.若一组数据1,3,5,a,8的方差是2,则另一组数3,9,15,3a,24的方差是 .
15.如果一组数据,,,的方差是7,那么一组新数据,,,的方差是 .
16.如果一组数据,,…,的方差是4,则另一组数据,,…,的方差是 .
17.如图是甲,乙两名射击运动员的次射击训练成绩的折线统计图.根据统计图可知甲,乙平均成绩均为环,则甲,乙的次射击成绩的方差,的大小关系是 .
参考答案:
1.B
【分析】先根据平均数计算公式列出算式进行计算,再根据平均数求出方差即可.
【详解】一组数据:3,4,4,5,4,6,2,4,4,4,
∴平均数,
方差.
故选:B.
【点睛】本题是对数据平均数和方差的考查,熟练掌握平均数和方差公式是解决本题的关键.
2.B
【分析】根据中位数的定义:将一组数据按照从小到大或从大到小的顺序排列,位于中间位置或中间两数的平均数即为中位数,因而,去掉一个最高分和一个最低分不影响中位数.
【详解】解:去掉一个最高分和一个最低分对中位数没有影响,而平均数、众数和方差均有可能改变,
故选:.
【点睛】本题考查了统计量的选择,解题的关键是了解中位数的定义,难度不大.
3.B
【分析】根据图标给出的数据得出,再根据中位数和众数的定义进行解答即可.
【详解】解:∵,
∴频率之和是,则这组数据的中位数是第6、7个数据的平均数,
即 吨,
∴对于不同的正整数x,中位数不会发生改变;
∵5出现的次数最多,出现了5次,
∴众数是5吨,
∴众数也不会发生改变;
而平均数与方差都会受到的影响而发生变化,
故选:B.
【点睛】此题主要考查统计的有关知识,主要包括平均数、中位数、众数、方差的意义.反映数据集中程度的统计量有平均数、中位数、众数方差等,各有局限性,因此要对统计量进行合理的选择和恰当的运用.
4.A
【分析】排序计算中位数,是一个常数,判断即可.
【详解】∵,
∴排序为或,
故中位数是,是常数,与“”的个位数字无关,
故选A.
【点睛】本题考查了中位数的计算即一组有序数组的中间数据或中间两个数据的平均数,熟练掌握定义是解题的关键.
5.A
【分析】经销商最感兴趣的是哪种鞋卖的多,根据众数的意义即可求解.
【详解】经销商最感兴趣的是哪种鞋卖的多,而众数就是一组数据出现次数最多的数,所以经销商最感兴趣的是这组数据的众数,
故选:A.
【点睛】本题考查了统计量中平均数、中位数、众数、方差的意义,能够根据题意来选择合适的统计量分析数据是解题的关键.
6.B
【分析】先由平均数的公式计算出的值,再根据方差的公式计算.
【详解】解:,5,3,,6,2平均数为4,
,
解得,
.
故选:B.
【点睛】本题考查方差的定义:一般地设个数据,,,的平均数为,则方差,它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
7.D
【分析】根据算术平均数、中位数、众数、方差的定义计算,即可得答案.
【详解】解: A、平均数为,故选项正确,不符合题意;
B、按照从小到大排列后为1,3,4,5,5,6,中位数为,故选项正确,不符合题意;
C、这组数据的众数为5,故选项正确,不符合题意;
D、方差为,故选项错误,符合题意.
故选:D.
【点睛】本题主要考查方差,众数,中位数,算术平均数,解题的关键是掌握众数、中位数、算术平均数及方差的定义.
8.A
【分析】根据平均数的定义:一组数据的总和除以这组数据的个数所得的商,叫做这组数据的算术平均数,简称平均数;众数的定义:一组数据中出现次数最多的数据;中位数的定义:一组数据中,处在最中间或处在最中间的两个数的平均数;方差的定义:一组数据中各个数据与它们平均数的差的平方的和的平均数,进行求解即可.
【详解】解:把这组数据从小到大排列为:25、26、27、28、30、30、30,处在最中间的数是28,
∴中位数为28,故A选项正确,符合题意;
∵30出现的次数最多,
∴众数是30,故B选项不符合题意;
由题意得它们的平均数为:
,故选项C不符合题意;
方差:,故D选项不符合题意;
故选A.
【点睛】本题主要考查了平均数,中位数,众数和方差,解题的关键在于能够熟知相关定义.
9.A
【分析】分别计算出原数据和新数据的平均数和方差,再进行比较即可得出答案.
【详解】解:原数据的平均数为:,
则原数据的方差为:
新数据的平均数为:,
则新数据的方差为:
,
平均数变小,方差变小,
故选:A.
【点睛】本题主要考查了平均数和方差,熟练掌握平均数和方差的计算公式是解题的关键.
10.D
【分析】根据选项,结合方差、平均数、中位数及众数的求法逐项验证即可得到答案.
【详解】A、原来数据的方差加入一个数后的方差一定发生了变化,不符合题意;
B、原来数据的平均数是=,加入一个数,平均数一定变化,不符合题意;
C、原来数据的中位数是3,加入一个数后,如果中位数一定变化,不符合题意;
D、原来数据的众数是2,加入一个数后众数仍为2,符合题意;
故选:D.
【点睛】本题考查统计量的计算,熟记方差、平均数、中位数及众数的求法是解决问题的关键.
11.(1)7,7.5,8,2.2
(2)选择乙运动员参赛
【分析】(1)根据表格中的数据求出乙的平均成绩、方差,找出甲的中位数,众数,确定出a,b,c,d的值即可;
(2)依据这两名队员的射击训练成绩的平均成绩相同,而乙运动员的成绩的方差比甲运动员的成绩的方差小,即可得到选择乙运动员参赛.
【详解】(1)乙的平均成绩(环);
乙成绩的方差
∵甲射击的成绩从小到大从新排列为:3、4、6、7、7、8、8、8、9、10,
∴甲射击成绩的中位数(环),
其众数;
故答案为:7,7.5,8,2.2;
(2)∵这两名队员的射击训练成绩的平均成绩相同,而乙运动员的成绩的方差比甲运动员的成绩的方差小,
∴选择乙运动员参赛.
【点睛】本题考查的是条形统计图和方差、平均数、中位数、众数的综合运用.熟练掌握平均数的计算,理解方差的概念,能够根据计算的数据进行综合分析.
12.(1)八(1)班平均分,八(2)班平均分
(2)八(1)班的成绩比较整齐,理由见解析
【分析】(1)根据算术平均数的概念求解可得;
(2)先计算出两个班的方差,再根据方差的意义求解可得.
【详解】(1)解:八(1)班的平均成绩是:(分);
八(2)班的平均成绩是:(分);
(2)解:八(1)班的成绩比较整齐,
理由:八(1)班的方差是:,
∵,即:八(1)班的方差小于八(2)班的方差,
∴八(1)班的成绩比较整齐.
【点睛】本题考查方差、平均数,解答本题的关键是明确题意,从统计图中准确寻找处信息.
13.(1)9,9
(2)8
(3)选乙运动员参加全市中学生比赛.
【分析】(1)根据众数和中位数的定义分别进行解答即可得出答案;
(2)先算出甲运动员5次的总成绩,再根据甲、乙两名运动员前5箭的平均成绩相同,即可求出乙运动员第5次的成绩;
(3)根据方差公式先求出甲和乙的方差,再根据方差的意义即可得出答案.
【详解】(1)解:∵9环出现了两次,出现的次数最多,则甲运动员前5箭射击成绩的众数是9环;
把这些数从小到大排列为:5,7,9,9,10,最中间的数是9,则中位数是9环;
故答案为:9,9;
(2)解:∵甲运动员的5次的总成绩是:(环),
甲、乙两名运动员前5箭的平均成绩相同,
∴(环);
故答案为:8;
(3)解:甲运动员的方差是:,
乙运动员的方差是:,
∵,
∴乙运动员的成绩比较稳定,应选乙运动员参加全市中学生比赛.
【点睛】此题考查了折线统计图.读懂统计图,从统计图中得到必要的信息是解决问题的关键.也考查了中位数、众数和方差的意义.
14.18
【分析】根据每个数据都放大或缩小相同的倍数,其平均数也有相对应的变化,方差则变为这个倍数的平方倍,从而得出答案.
【详解】解:∵一组数据1,3,5,a,8的方差是2,
∴另一组数据3,9,15,3a,24的方差是.
故答案为:18
【点睛】本题考查方差的计算公式的运用:一般地设有n个数据,,,…,若每个数据都放大或缩小相同的倍数后再同加或同减去一个数,其平均数也有相对应的变化,方差则变为这个倍数的平方倍.
15.28
【分析】设已知数据的平均数为,根据数据的方差列出关系式,进而求出新数据的平均数,得出方差即可.
【详解】解:∵一组数据,,,的方差是7,平均数为,
∴,
∵,,,的平均数为,
∴
,
故答案为:28.
【点睛】此题考查了方差,以及平均数,熟练掌握各自的算法是解本题的关键.
16.4
【分析】根据当数据都加上一个数(或减去一个数)时,方差不变,即可得出答案.
【详解】∵一组数据,,…,的方差是4,
∴另一组数据,,…,的方差也是4.
故答案为:4.
【点睛】此题考查了方差,熟记当数据都加上一个数(或减去一个数)时,方差不变,即数据的波动情况不变是解题的关键.
17.
【分析】从折线图中得出甲乙的射击成绩,再利用方差公式计算即可.
【详解】解:由图可知,
甲的成绩为,
乙的成绩为
,
,
∴,
故填:.
【点睛】本题考查方差的计算,熟练掌握平均数和方差的计算公式是解题的关键.
备战中考数学《重难点解读•专项训练》专题06 四点共圆(专项训练): 这是一份备战中考数学《重难点解读•专项训练》专题06 四点共圆(专项训练),文件包含专题06四点共圆专项训练原卷版docx、专题06四点共圆专项训练解析版docx等2份试卷配套教学资源,其中试卷共26页, 欢迎下载使用。
备战中考数学《重难点解读•专项训练》专题04 定弦定角(专项训练): 这是一份备战中考数学《重难点解读•专项训练》专题04 定弦定角(专项训练),文件包含专题04定弦定角专项训练原卷版docx、专题04定弦定角专项训练解析版docx等2份试卷配套教学资源,其中试卷共23页, 欢迎下载使用。
备战中考数学《重难点解读•专项训练》专题03 阿氏圆(专项训练): 这是一份备战中考数学《重难点解读•专项训练》专题03 阿氏圆(专项训练),文件包含专题03阿氏圆专项训练原卷版docx、专题03阿氏圆专项训练解析版docx等2份试卷配套教学资源,其中试卷共14页, 欢迎下载使用。












